伺服系统转动惯量辨识及控制器PI参数优化

孙彦瑞，苏成志

(长春理工大学机电工程学院，长春 130000)

0 引言

机器人在运行时，每个轴的负载转动惯量与负载扭矩随着机器人的姿态的变化而变化；伺服系统对负载转动惯量的辨识精度、辨识快慢，决定着伺服系统运行的稳定性、精确性与快速性。伺服系统不能精确、高速地辨识负载转动惯量，在机器人运行时电机容易出现振荡与谐振的现象，控制系统内部参数与实际工况不符。如果转动惯量辨识值过大可能使系统不稳定，响应慢；如果转动惯量辨识值过小，系统响应会加快，但系统会产生超调或震荡的现象，甚至会造成低速时的转矩脉动的现象[1]。针对此问题，如何更好地实时辨识伺服系统负载转动惯量值，是解决伺服系统运行不稳定的关键。

国内外的很多学者对伺服系统转动惯量的辨识已经研究出了很多的成果。Kweon T J 等采用全阶Luenberger观测器[2]，其中全阶观测器会受到转动惯量的初始值影响，并且在最严重的情况下，系统将会不稳定运行。Guo Y运用模型参考自适应方法(MRAS)来对转动惯量进行辨识[3]，该方法需要高精度的速度信息，并且低速时有很大的误差。Campos M D采用卡尔曼滤波器(Kalman filter)对负载转动惯量与负载扭矩进行观测，但是协方差矩阵很难建立[4]。Li Niu使用定阶递推经验频域最优参数估计(Fixedorder Recursive Empirical Frequency-domain Optimal Parameter Estimation)辨识负载转动惯量与负载扭矩信息，具有较高的鲁棒性，但是该方法在频域内计算很复杂[5]。文献[6]提出基于规则的参数整定方法，该方法是通过设计某一种规则，对系统的响应性能进行量化评价，从而得到最优的参数整定的方法，包括模糊控制法、遗传算法和评价函数法等，但此类方法由于整定时间长、参数评价准则确定困难等原因，并没有被广泛的应用到永磁同步伺服系统中。

综上所述，传统转动惯量辨识算法容易受到初值精度、误差与计算复杂的影响，往往不能得到高精度的辨识值。在伺服系统参数辨识领域，很多专家与学者运用群智能优化算法进行参数辨识，首先估计待辨识参数范围并初始化解空间，然后将参数的辨识问题转化为优化问题，利用智能优化算法求出最优解[7]。例如， Wang Shaowei运用蚁群算法去辨识转动惯量与负载扭矩，但是容易陷入局部最优解[8]。粒子群优化算法(PSO)是一种群智能优化算法，其实现简单、灵活，可用于求解优化问题[9]。

本文综合分析了传统转动惯量辨识算法实现的各种约束条件，主要从算法初值影响程度、实现难易程度与辨识精度的角度分析，引入粒子群优化算法来解决转动惯量实时辨识问题。在粒子群优化算法中固定的学习因子，会导致算法解的精度低和辨识过程收敛速度慢的问题，针对此缺陷[10]，引用一类非线性动态学习因子粒子群算法(Nonlinear dynamic learning factor particle swarm optimization，NDLFPSO)[11]，使辨识过程更快收敛、辨识解的精度更高。运用该算法在线辨识转动惯量与负载扭矩，并运用在线辨识的转动惯量进行修正速度控制器PI参数，使控制系统更加精确趋近于真实的系统模型。

1 伺服电机数学模型建立

在id=0的矢量控制模型中，永磁同步伺服电机的运动方程可以表示为：

Te是电机输出电磁转矩，Te=KTiq，KT是电磁转矩系数；TL为电机的负载转矩；J为电机轴与负载转动惯量之和；B为粘滞摩擦系数；ω为电机转子旋转角速度；θ为旋转角度。

通常，伺服系统运用id=0控制方式，通过建立系统传递函数模型，可以得到id=0下的永磁同步电机的数学模型如图1所示。

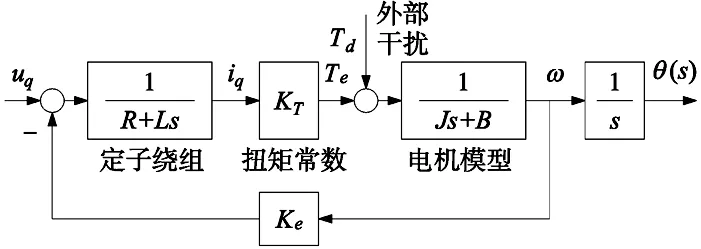
图1 id=0永磁同步电机的数学模型

2 参数辨识策略

2.1 转动惯量与负载扭矩辨识策略分析

将粘滞摩擦系数忽略，伺服系统模型为:

设置负载转矩、转动惯量的参数值范围，初始化粒子群的二维解空间，分别定义横轴为转动惯量、纵轴为负载扭矩。在每一次的迭代过程当中，粒子需要根据适应度函数初始化全局最优解，最后优化计算出一个适应度最小的全局最优解。

采集离散点Pi{ω(i),Te(i)}，i=1,2,...,M。根据最小方差原理，适应度函数为[7]：

2.2 基于非线性动态学习因子的粒子群优化算法

2.2.1 标准粒子群优化算法

对于一个D维的优化空间，由n个粒子组成。该粒子代表着候选解，每个粒子在D维空间中都初始化各自的速度与位置信息，根据算法每次迭代，重新根据适应度值更新每个粒子的位置与速度。则更新的公式：

θid(k+1)=[ωθid(k)+c1r1(pid(k)-xid(k))+
c2r2(pgd(k)-xid(k))]

xid(k+1)=xid(k)+θid(k+1)

上式中，i=1,2…n，d=1,2…n，θid(k)代表粒子速度，xid(k)代表粒子位置，pid(k)代表局部最优粒子，pgd(k)代表全局最优粒子，ω代表迭代过程中的惯性权重，c1、c2代表粒子学习因子，r1、r2代表在[0,1]内产生的随机数。

2.2.2 基于非线性动态学习因子粒子群优化算法介绍

由于标准粒子群优化算法学习因子c1、c2在[0,2]间的定值，在求解复杂问题时标准算法中的粒子在迭代前期容易出现“扎堆”的现象，使算法容易陷入局部最优解[11]。动态的学习因子c1与c2有助于获取全局最优解，快速跳出局部最优解。在迭代求解的前期，算法对c1的取值较大，对c2的取值较小，是因为此过程在前期可以加强个体粒子学习能力，避免粒子过于集中在某个区域内，并陷入局部最优解的状况；在迭代计算的后期，算法取较小的c1值，对c2的取较大的值，进而加强粒子向群体的自学习能力，使大量的粒子向全局最优解移动并且提高全局最优解的精度。

粒子速度更新公式改为：

θid(k+1)=[ωθid(k)+c1r1(pmd(k)-xid(k))+

c2r2(pgd(k)-xid(k))]

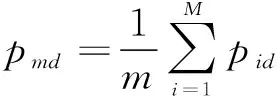
当t<0.6×Tmax时：

c2=0.4+0.1×rand

当t>0.6×Tmax时：

c1=0.4+0.1×rand

上式中，t代表当前迭代次数，Tmax代表最大迭代次数。

2.2.3 算法仿真分析

永磁同步电机仿真在MATLAB中的SIMULINK中仿真分析，电机参数如表1所示。

表1 仿真与实验所用的电机系统参数表

待辨识的转动惯量J = 0.002 1 kg·m2，负载扭矩TL=2.5 N·m，初始化粒子群优化算法2维空间：[Jmin,Jmax]=[0.001,0.008]、[TL min,TL max] = [0,8]，采样次数：10次，粒子个数：50个，惯性权重ω=0.9。

电机从0～2000 r/min大约需要0.02 s，则设置采样时间为T=2ms，运用标准粒子群优化算法对转动惯量与负载扭矩进行辨识，如图2所示。

图2 参数辨识进程

从图2可以看出，横轴代表算法迭代次数，纵轴代表每一次迭代时产生的全局最优值所对应的适应度值，适应度值逐渐趋近于0，代表逐渐收敛全局最优解。随着粒子迭代次数可以得到：图3可以看出在0代～20代，粒子移动较快，个体粒子学习能力较快，向局部最优靠近；图4表示20代～40代，粒子移动速度放缓，粒子在邻域内靠拢；图5表示40代～60代，粒子向全局最优解移动；图6表示从60代以后的粒子移动至一点，完成选取全局最优点。

图3 初始化粒子群二维空间 图4 迭代20次时粒子分布

图5 迭代40次时粒子分布 图6 迭代60次时粒子分布

上图对改进粒子群优化算法辨识转动惯量与负载扭矩各个迭代的阶段进行表示，结果转动惯量J=0.002 18 kg·m2，其相对误差是3.6%；负载扭矩TL= 2.2 N·m，其相对误差-3.5%。

3 基于粒子群优化算法的速度控制器参数整定分析

3.1 速度环PI控制器参数整定原理

根据上述通过粒子群优化算法在全局搜索最优粒子，最优粒子代表着理想的PI控制器的参数值，然后实时修正PI控制器的比例与积分参数，进行伺服系统速度环PI控制器参数的实时整定。基于PSO算法对PI控制器参数整定示意图如图7所示。

图7 基于PSO算法对PI控制器参数整定

3.2 PI参数整定过程分析

把实时辨识的转动惯量应用在PI参数整定过程当中，可以改善伺服系统运行中的稳定性、精确性与抗扰动性能。伺服控制系统的组成一般外环速度环、内环电流环[1]。把电流环化简成惯性环节，速度控制环就可以等效成为二阶系统。简化后的等效速度控制环如图8所示。

图8 速度环等效框图

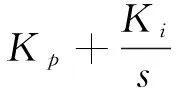
根据图8，等效后伺服系统速度环开环传递函数表示为：

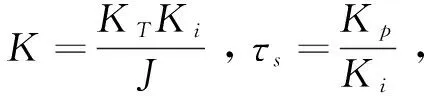
上式是典型的Ⅱ型系统，根据经典控制理论的分析，使上式的系统在稳定性和响应速度方面都具有较好的特性。一般要求[12]：

代入Ki、Kp可以求得：

上式中，KT、τi都为常数。可以看出速度环PI控制器比例Ki与积分Kp参数只取决于转动惯量的变化并且呈线性比例关系。伺服系统转动惯量对速度环PI参数根据上式进行修正，即可以实现控制器参数的自整定。

4 转动惯量辨识仿真分析

运用上文Simulink建立永磁同步伺服电机矢量控制模型，并运用基于非线性动态学习因子的粒子群优化算法，实时辨识转动惯量。运用仿真实验，验证了该方法对系统性能优化的有效性。给定测试信号，转速在1500 r/min匀速运动、在0.1 s时输入2 N·m干扰扭矩，并且对应的负载转动惯量为J=0.003 4 kg·m2。

如图9所示是基于非线性动态学习因子的粒子群优化算法对转动惯量进行辨识，在迭代50次是转动惯量逐渐趋于给定值；在迭代50次以后与给定值对比最大误差为2.1%，该精度满足伺服系统的速度控制器PI参数自整定的要求。

图9 非线性学习因子的粒子群优化算法实时辨识转动惯量

为了模拟电机在机器人上面的工作情况，需要设计实时变化的模拟负载。设定负载扰动函数r(t)=2sin(5t) N·m，以时间为变量的正弦函数。如图10所示，蓝色线代表运用普通粒子群优化算法辨识PI参数的伺服电机模拟的速度输出曲线，而橙色线代表运用改进粒子群优化算法辨识PI参数的伺服系统模拟的速度输出曲线；在施加相同的负载下，转速波动情况明显有很大区别，改进后的算法与普通算法在PI参数辨识的应用相比较，电机启动超调量明显减小，在运行过程中更加稳定在设定速度附近，在变负载运行过程当中，最大速度误差减小5.6%。

图10 基于不同辨识算法下的速度反馈

如图11所示电机在模拟运行过程当中，电机对应的q轴电流图，改进后算法与普通算法在PI参数辨识中的应用相比校，启动电流明显减小，在运行过程当中输出电流的波动小很多。

图11 伺服电机q轴电流输出

5 结论

本文提出基于非线性动态学习因子的粒子群优化算法，对伺服系统负载参数实时辨识。根据实时辨识的转动惯量值，来修正速度控制器PI参数；该算法在仿真实验中表现性能优良，减小电机在启动时速度超调量，使电机启动更加稳定、快速，并且在变负载实验情况下，输出速度的波动相对较小。综合分析该方法具有更快的响应速度、更高的控制精度以及更强的抗干扰能力，对机器人等设备的运动控制系统提供重要的保障。