最大流算法应用于二次线性规划布局合法化过程

（无锡中微亿芯有限公司，江苏无锡 214072）

1 引言

现场可编程逻辑门阵列（Field-Programmable Gate Array,FPGA）是一种在日用家电、大型机械乃至航空航天领域都有广泛应用的芯片。而FPGA 的设计离不开电子设计自动化（Electronic Design Automation,EDA）工具。布局则是EDA 工具中重要的一环，其对EDA 工具本身运行速度、所处理电路的最终质量有着很大影响。

近年来，FPGA 芯片电路的规模快速增长，使其功能更加强大，但同时也给相应的EDA 工具带来了挑战。解析型的算法以其可以使用数学方法快速求得全局最优解的特性成为当今布局算法的主流方向之一。二次线性规划算法[1-2]是解析型算法的一种，其在具体应用于解决布局问题的时候体现出了快速求解的特性，但在求解完成后，依然存在不合法的布局，需要再次进行合法化操作。原始的合法化操作仅是在不合法布局的周围寻找一个最近的合法位置，这样的操作不具备任何导向性，往往导致最终的解不尽如人意。业界有使用综合型算法[3]来弥补这一缺点，本文则将最大流算法应用于二次线性规划算法求解后的合法化操作，以求提高最终解的质量。

2 原始合法化流程概述

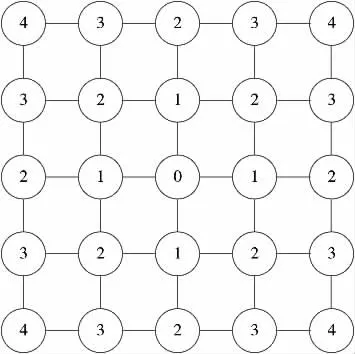
图1 曼哈顿距离示意图

3 最大流算法原理

如图2 所示是最大流算法中一个经典问题——两方匹配问题。每个节点有自己可以放入的位置，位置个数有限，要使尽量多的节点可以放入。将布局合法化问题抽象成图，将不合法节点与空置位置抽象为图中节点，将不合法节点与空置位置间的关系抽象为边。为每一个不合法节点建立一个节点，为每一个空置位置建立一个节点，在其间建立有向边代表不合法节点可以放入该空置位置；建立一个虚拟的源点S，在S 与每个不合法节点间建立有向边；建立一个虚拟的终点T，在每个空置位置节点与T 之间建立有向边；这样布局合法化问题就变成了求解由S 到T 的最大流。为了使寻找的过程具有导向性，使用线长来进行评价并给每条不合法节点到空置位置的边赋权值，记为cost。这样又进一步将布局合法化问题转化为了最大流算法中的Min-Cost Max-Flow 问题。

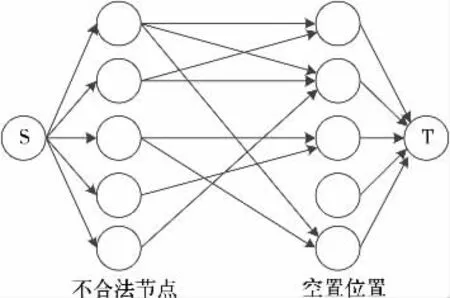
图2 两方匹配问题示意图

Min-Cost Max-Flow 问题的求解过程如下：

(1)在剩余图中寻找cost 最小的路径；

(2)对路径进行增广，形成新的剩余图，具体到布局合法化问题中即将（1）中所找到的路径上所有的边反向，并将这些边的cost 取负；

(3)不断重复（1）、（2），直到S 到T 不存在路径，所得到的图即为流最大，且在相同流量情况下cost 最小的图。

上述过程使用了Ford-Fulkerson[4]算法以确保最终找到最大流，并可以使用数学归纳法简单证明求解过程每次循环都找出了当前流量下cost 最小的流，数学归纳法的证明过程如下：

(1)流量为1 时，显然成立；

(2)设流量为i 时，f 是cost 最小的流，则其剩余图中必不含有负cost 的环路；

闲暇时，黄婉秋喜欢翻阅介绍养生保健知识的书籍，记一些容易做到的保健方法。因此，她的生活起居有了些讲究：“我根据自己的体质，少吃苹果、酸菜等食物，因为苹果会产生胃酸，酸菜对牙齿不好。每天起床时，我都做到‘三个一’：在床上躺一分钟、坐一分钟，起床后站一分钟，这都是从保健书上学来的。”

(3)由求解方法推导出的流量为i+1 时的流记为g，则g-f 为一条S 到T 的cost 最小的路径，将该路径记为r；

(4)若在流量为i+1 时存在比g cost 更小的流h，则对于这两个流量相同的流，h-g 必存在环路，又因为h 的cost 小于g，则h-g 的环路中必包含至少一个负cost 的环路，则h-f 是路径r 与存在负cost 环路的若干环路组成，即f 的剩余图中存在cost 为负的环路；

(5)f 的剩余图中存在cost 为负的环路，则f 不是流量为i 时cost 最小的流，这与假设条件相悖；

(6)所以流量为i+1 时g 即为cost 最小的流，原结论得证。

4 最大流算法实现

合法化过程的流程图如图3 所示。

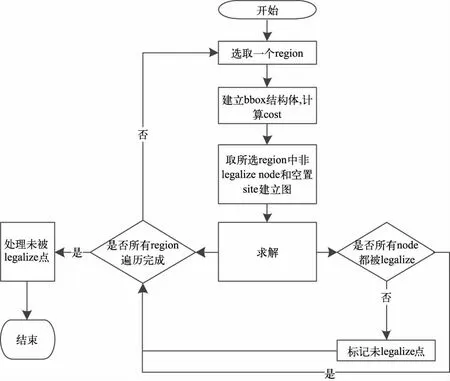
图3 合法化过程流程图

将FPGA 划分为若干区域，并对每个区域分别进行合法化。合法化按照一定大小的区域分开多次进行是因为寻找最大流的Ford-Fulkerson 算法、寻找最短路径的dijkstra[5]算法两者叠加使用，使得算法运行时间随算法中节点数量增加呈指数级上升，分开多次求解虽然在一定程度上限制了解的范围，但避免了算法带来的不可接受的时间成本。

首先需要选取一个FPGA 中的区域。随后按照当前的布局状态建立bounding box 结构以线长为目标计算cost，该结构以边界位置、位于边界上的节点数量来记录线网的状态。这样做的好处是，只有少数情况下需要遍历线网中所有的节点来得出半周长。线网半周长再乘以线网大小所决定的影响因子即得到该线网的线长。记线网中节点个数为n，当n≤3 时，影响因子为1。当3＜n≤50 时，影响因子计算如式（1）所示。

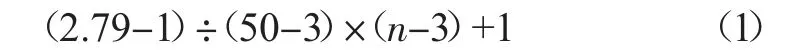
当n＞50 时，影响因子计算如式（2）所示。

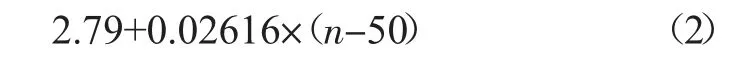
对所选取区域中的布局状态进行抽象，建立图。除了按照第2 节的方式建图，还需要使用前一步所计算的cost 为每一条不合法节点到空置位置的路径赋值。此外，为了更高效地寻找cost 最小的路径，选取了dijkstra 算法，而dijkstra 算法不允许图中路径出现负值，因此要为每一个图中节点加势，使可能含有负cost路径的图转化为不含有负cost 路径的图，以适用dijkstra 算法。之后再依照第2 节所述方法进行求解，为该区域中的非法节点寻找最优的合法空置位置。

在一个区域合法化完成后，再选取下一个区域重复以上操作，直至所有区域遍历完成，布局处于合法状态。

由于区域中资源有限，在一个区域中有可能出现资源耗尽时仍有节点处于非法放置状态。先将这些节点标记，待所有区域遍历完成，再将所有区域中的这些个别非法节点一次性处理，使其合法。处理的过程以剩余非法节点和剩余空置资源建立图，求解。

5 实验结果及讨论

文章选取了13 个测试电路，在yxc3 的jyxlx350tff1738 器件上使用原始合法化方法和不同划分区域大小的改进型算法在完全相同的环境下进行布局。以布局后线长为标准评价最终电路质量，测试结果如表1 和表2 所示。

所选取的电路slice 使用率从2%至98%不等。其中3des_vhdl 与igt_single_cpuv3 的slice 使用率小于10%；igt_quad_cpuv3、igt_noc_10v3、igt_noc_3v3、igt_ten_cpuv3 的slice 使用率在10%到40%之间；igt_noc_4v3、igt_noc_5v3、s1_core_no_dsp、s1_core_with_dsp 的slice 使用率在40%到70%之间；igt_noc_6v3、igt_fixpt_cordicv3、igt_float_cordicv3 的slice 使用率超过70%。

从表1 和表2 中可以看出，改进后的算法不论如何选取区域以布局后线长为标准进行评价都有普遍的提升，但布局过程的运行时间都有不同程度的增长。线长方面呈现出选取区域面积越大最终线长越小的趋势。运行时间方面，区域选择过小或过大都使运行时间显著增长。其中，区域大小为4×4 时与原始合法化方法相比平均增加运行时间34%，减少线长2.1%；区域大小为8×8 时与原始合法化方法相比平均增加运行时间12.5%，减少线长3.1%；区域大小为16×16 时与原始合法化方法相比平均增加运行时间21.8%，减少线长4.1%；区域大小为32×32 时与原始合法化方法相比平均增加运行时间96.7%，减少线长4.6%；区域大小为FPGA 自身region 时与原始合法化方法相比平均增加运行时间75.4%，减少线长4.3%。综合来看，选取区域大小为8×8 或16×16 较为合适。

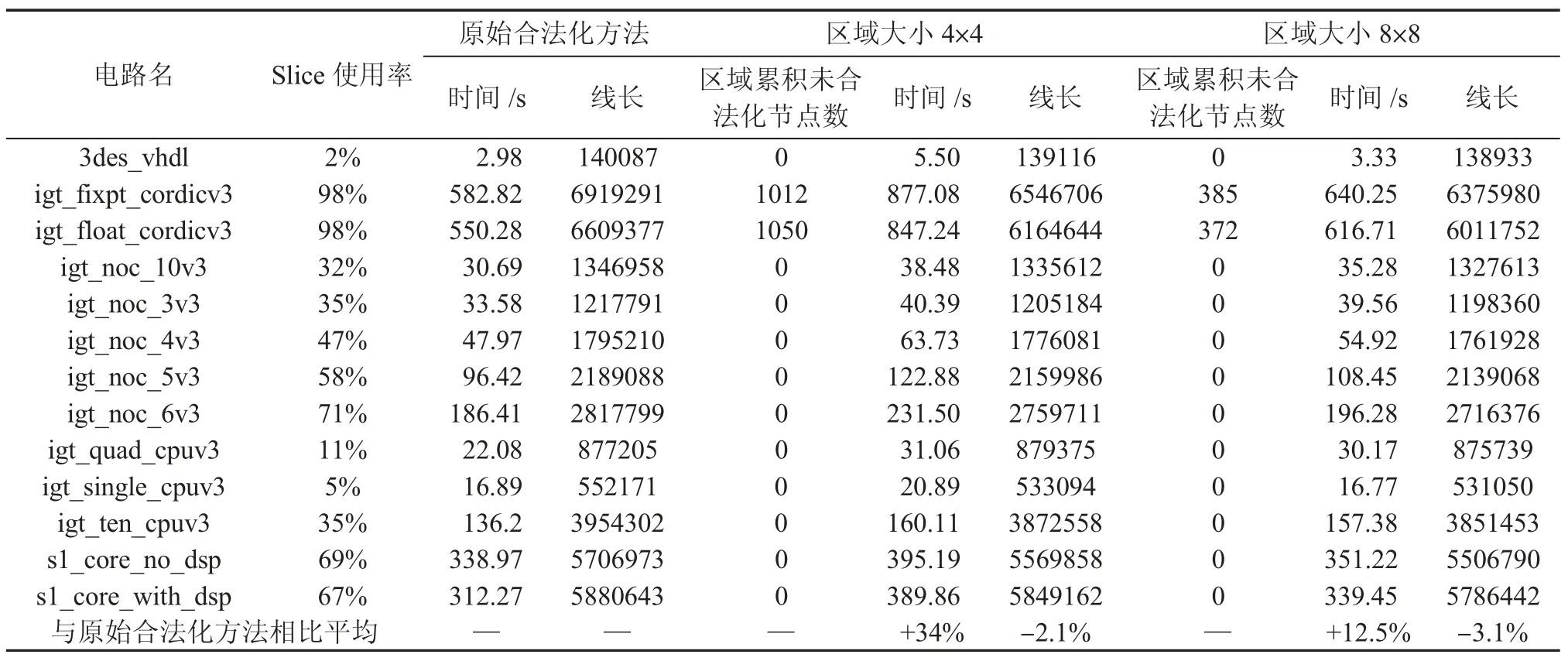
表1 布局时间及线长测试结果表

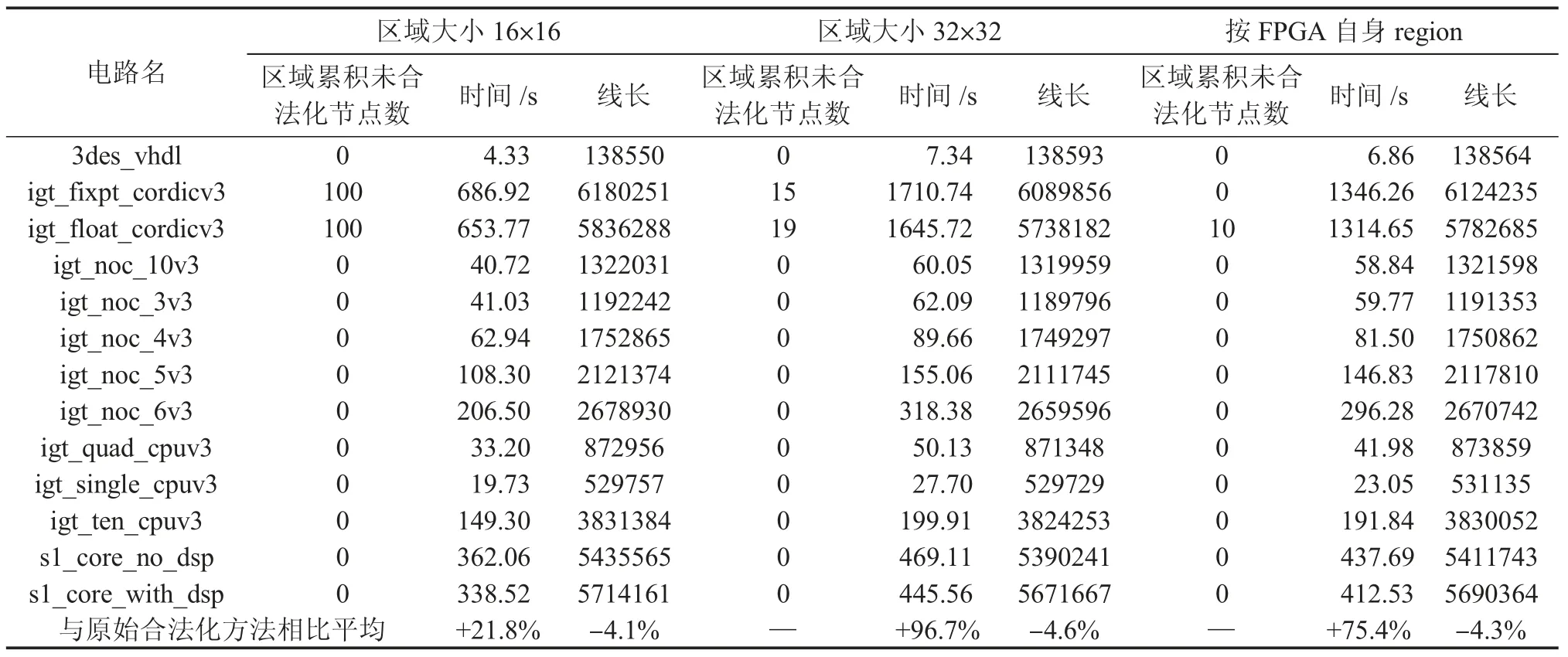
表2 布局时间及线长测试结果表（续）

6 结论

本文将最大流算法应用于二次线性规划算法的合法化部分，使原本不具有导向性的合法化流程变得具有导向性，并在一定程度上提高了最终解的质量。今后将尝试在算法中加入时序驱动，以适应更多的需求。