直升机载火控雷达抗干扰捷变波形优化算法

余唐旭，张劲东，何 涛，李 晨

（1.中国直升机设计研究所，景德镇333001；2.南京航空航天大学电子信息工程学院，南京211106；3.中航工业雷华电子技术研究所第六研究部，无锡214063）

直升机载火控雷达能够实现对地对空目标监视、跟踪、定位和地形回避［1］，且具有频段高、体积小和质量轻等特点，是武装直升机适装的重要电子装备［2］。随着新的电子干扰技术的迅速发展，低空近程防空武器系统以及直升机专用雷达综合对抗系统的出现，导致直升机载雷达工作的电磁环境日趋复杂［3］。发射固定波形的雷达一旦其信号被敌方干扰机截获和识别，将非常容易被实施有针对性的干扰。

捷变波形由于其发射波形的不确定性，会使敌方干扰机的分选识别变得非常困难，因此也难以对其实施有效干扰［4］。随着数字波形发生器技术的不断发展，捷变波形逐渐成为雷达研究领域的新热点和直升机雷达波形的新选择。针对复杂波形设计问题，He 等给出了用于设计模糊函数的Multi-CAN 算法［5］，Arlery 等给出了基于梯度下降的模糊函数设计算法［6］。Boyd 等提出求解凸优化问题的交替方向乘子法（Alternating direction method of multipliers，ADMM）［7］。随 后Liang 等 使 用AD-MM 方法求解带约束二次型最优化问题，给出了一种设计具有低自相关旁瓣的连续相位调制信号方法［8］。在二次型优化问题中，ADMM 更新公式可以给出闭式解，但在四次型优化问题中，闭式解难以获取。Hunter 和Lange 提出的Majorization-min-imization（MM）算法是一种迭代求解最优化问题的算法，通过构造并求解形式更为简单的辅助函数，逐渐逼近原问题的最优解［9］。Song 等给出了一种基于MM 算法的模糊函数设计方法，其中辅助函数为目标函数上界的二次型［10］。Kerahroodi等［11-12］将坐标下降（Coordinate descent，CD）算法运用到优化波形自相关函数。CD 算法在整个迭代过程中使用不同的坐标方向进行线搜索以求得目标函数的最优解。以上优化方法主要用于单个波形优化。捷变波形的优化问题目前主要依赖启发类智能优化算法，例如模拟退火算法［13］、遗传算法［14］和粒子群算法［15］等，但在面对超高维优化变量时，往往优化耗时太长，容易陷入局部收敛。

由于直升机载火控雷达作用距离相对较近，且普遍采用中高重复频率的窄脉冲，因此其相干处理间隔（Coherent processing interval，CPI）虽然脉冲个数较多，但单个脉冲码长较短，影响其探测性能。如何有针对性地开展高维变量下捷变波形优化设计，使其在低复杂算法下实现捷变优化的同时，保证多脉冲和短码长下的相干处理性能是本文的研究目标。目前针对短码和捷变波形优化的工作相对较少。本文基于捷变相位调制波形（Agiled phase coded waveform，APCW），以离散化的捷变波形距离-多普勒模糊函数为优化目标，将捷变波形设计问题建模为带约束四次型最优化问题，并给出基于SVD 降维算法和循环算法的求解方法。

1 捷变波形模糊函数

设直升机载雷达系统在一个CPI 内连续发射N 个脉冲信号

脉冲多普勒体质雷达对回波信号首先进行滤波处理。对于反射的第n个脉冲，接收滤波器可写为

则滤波器的输出为

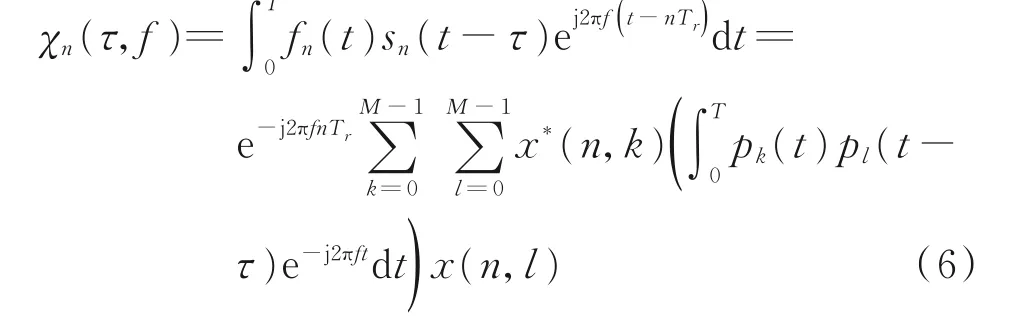
式中：τ 和f 分别为目标时间延迟和多普勒频移。

由于直升机载火控雷达的脉冲重复频率较高，因此在目标的相对径向运动速度满足|v|≤λ/4Tr的情况下，目标的多普勒移频能够满足-1 2Tr≤f ≤1 2Tr，其 中λ 为 波 长。同 时 直 升机载火控雷达为了满足最小作用距离和最大作用距离要求，往往采用窄脉冲和低于1/5 的占空比。因此，对于其发射波形的持续时间足够小，满足|2πfT| ＜π 5，即T ≤Tr5。由此，可以不考虑动目标（包括地面和低空飞行目标，以及在高重频下的弹目标）多普勒频率引起的回波脉内相位变化。

取τ=ptp，p=-M，…，1，…，M。由于Tr≫tp，χn(τ，f )可转换为

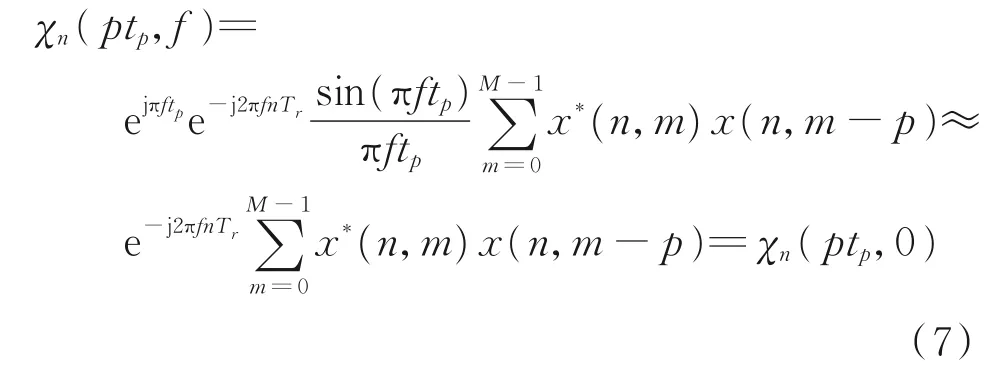
式（7）忽略了多普勒频率对脉内相位的调制。

回波信号经过滤波之后，滤波器输出可表示为一个2(M -1)×N 的二维矩阵ξ( p，v)，2(M -1)和N 分别对应了时间延迟和脉冲数目。接着，对滤波结果进行一维N 点逆离散傅里叶变换以实现固定延迟脉冲信号的相干处理。经过处理后的距离-多普勒二维函数为

从优化模糊函数的角度来说，捷变波形的期望模糊函数除了主峰，在其余位置的副瓣接近零。由式（9）所示，目标的多普勒频率f仅影响距离-多普勒平面上目标所在位置的聚焦，不影响目标在距离-多普勒二维平面上的形状，即模糊函数形状。因此可以设置f =0，且定义捷变波形的离散距离-多普勒模糊函数为

为抑制杂波和旁瓣，则需最小化目标函数ξ( p，q)

由于捷变波形的设计本质上是一个高维复杂变量的约束优化问题，对其进行直接求解优化难度极高，且维度高造成的计算复杂度也极高。因此，这里采用交替指向方法首先将上述优化分解为多个最小化问题。显然，降维后的优化问题在一次优化过程中的优化变量个数明显减少。

2 基于SVD 分解的捷变波形优化算法

降维后的捷变波形优化问题简化为交替指向下各个波形的单个优化。但对单个波形的优化，问题（12）仍是一个四次型的优化问题。直接对四次型的优化是一个非常复杂且耗计算量的问题。因此，针对捷变波形优化设计，首先采用一种基于奇异值分解的优化设计方法。该方法构造自相关系数矩阵作为中间量，在优化过程中通过先优化自相关系数矩阵，再优化波形，最后通过反复迭代的方式实现收敛。与文献［7-8］等方法相比，是一种新的将四次型降为二次型的思路。

2.1 交替指向下的相关系数估计

2.2 SVD 降幂次

在估计各个波形的相关系数后，虽然解决了优化的高维数问题。但优化目标仍是一个四次型优化问题，这里采用SVD 分解进行降幂次。

令

对式（20）进行最小化，可以按照以下方法进行分解和优化。

2.3 基于SVD 的捷变波形优化流程

根据上述过程，对捷变波形的优化可以总结为如下所示。

3 基于循环算法的捷变波形优化算法

在第2 节中，对捷变波形的优化其核心在SVD分解的运用，因此其计算复杂度略高。在针对短码的优化，SVD 运算也相对较好。在某些不希望采用复杂运算形式的场合，SVD 分解的适用性将下降。为了简化运算形式，本节将采用一种循环算法的捷变波形优化算法，该算法最大的特点在于运算形式较为简单，不涉及矩阵分解等复杂运算。

3.1 优化模型的转化

捷变波形的优化目标函数为四次型，因此很难利用解析形式给出全局最优解或直接给出优化方法。这里给出一种局部最优的优化技术，这是一种计算效率较高的方法。

式中：矩阵Qn为M ×M 的Hermitian 矩阵 为正定矩阵。

3.2 循环迭代的算法证明

从上述证明过程可见，如果两个不等式的约束能够满足，就能够保证目标函数的收敛性。定理3将证明如何保证这两个不等式的成立。

定理2 两个不等式成立

由此可见，上述过程满足了两个不等式的要求，可以使得上述过程在迭代过程中保证计算的收敛性。

考虑到序列的恒模性约束，近似解可以表示为

3.3 基于循环算法的捷变波形优化流程

循环算法步骤总结如下。

步 骤 1 令 k=0，初 始 化 调 制 编 码{ x(n，m) }，n=0，1，…，N -1；m=0，1，…，M -1，使用随机生成的编码调制形式；

步骤2 令n=0；N -1；

步骤2.1 根据公式计算矩阵Qn；

4 计算机仿真与性能分析

选取参数：直升机载火控雷达载频35 GHz，重频100 kHz，带 宽10 MHz，一 个CPI 内 脉 冲 个 数100，脉宽在0.8～2 μs 之间变化，即对应的脉内编码码长M 在8～20 之间变化。

目 标 区 域Φ 的 参 数 为Φ={( p，q)|-M/2 ≤p ≤M/2，-N/4 ≤q ≤N/4}。

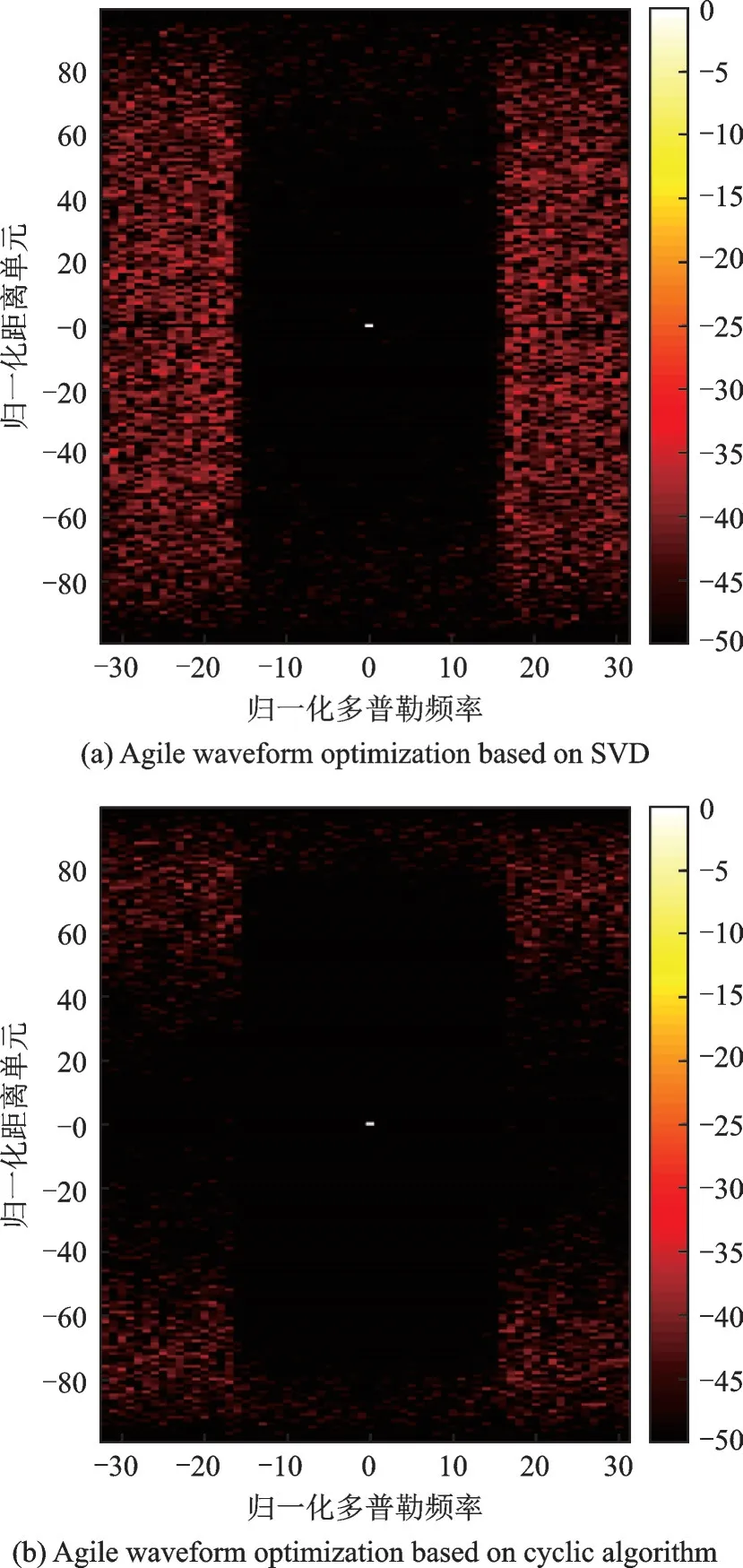
图1 基于SVD分解和循环算法的优化后的模糊函数俯视图Fig.1 Top view of optimized ambiguity function based on SVD and cyclic algorithm

图1 给出了脉冲个数100 和码长20 下的基于SVD 分解和循环计算的捷变波形优算法优化后的模糊函数俯视图。

图2 给出了基于SVD 分解和循环计算的捷变波形优算法的收敛。由图2 可见，基于SVD 分解的方法收敛速度更快，基于循环计算的方法收敛速度稍慢，但在经过400 次迭代计算后二者优化性能接近。

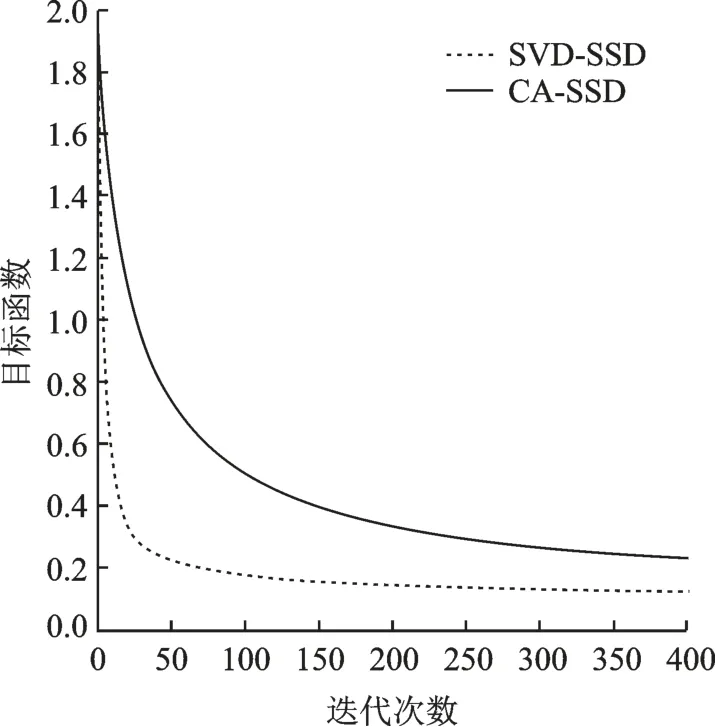
图2 捷变波形优化算法的收敛曲线Fig.2 Convergence curve of agile waveform optimization al-gorithm

图3 给出了在迭代100 次后不同算法在不同M 下的优化性能，可见基于SVD 的优化算法结果优于基于循环计算的算法。

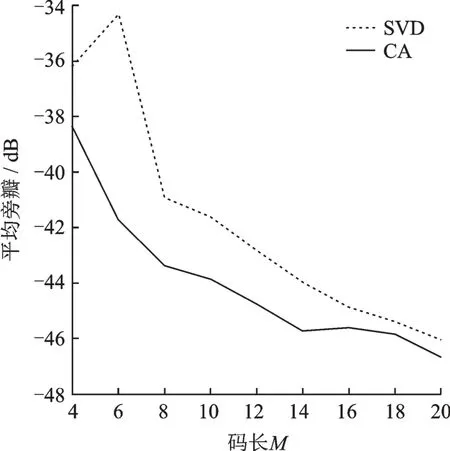
图3 在不同M 下的捷变波形优化性能Fig.3 Agile waveform optimization performance using dif-ferent M

图4 给出了脉冲个数100 和码长20 下捷变波形对多目标的处理结果。由图4 可见，LFM 和随机捷变波形的副瓣整体较高，其中随机捷变波形的副瓣分散，LFM 波形的副瓣呈现十字形。经过优化后的捷变波形副瓣整体较低。

图4 捷变波形对多目标的处理结果Fig.4 Results of multi-target processing with agile wave-form

5 结 论

本文针对直升机载火控雷达在多脉冲和短码长下的捷变波形优化设计问题，提出了具有目标区域低旁瓣模糊函数的捷变相位编码波形优化设计算法。算法通过SVD 分解和循环计算框架求解带约束的四次型优化问题。其中SVD 分解的波形优化算法收敛性更好，循环计算的波形优化算法计算简单，不涉及复杂运算形式。仿真结果表明，两种算法在设计脉冲串性能上接近，但SVD 分解算法收敛速度更快，循环计算算法具有更高的运算速度。