升降平台跌落对起落架过载的影响
郝志福,王秀霞,沈 伟,胡国才
(烟台南山学院航空学院,龙口265713)
用升降平台实施对直升机转运时,为保证升降过程中直升机的稳定,须对其进行系留。若平台在升降中遇到意外情况发生跌落,可能会使直升机受到冲击而导致损伤或损毁。
平台跌落时直升机受到的冲击状态与着陆冲击状态有显著不同。直升机着陆时旋翼具有较大升力,同时起落架处于完全伸展状态,着陆时的压缩行程动载荷低并可吸收较大的冲击能量,而在回弹行程可消耗大部分能量,从而将着陆冲击载荷限制在允许的范围内[1]。升降平台跌落时,直升机处于停机系留的无升力状态,在自重和系留载荷作用下起落架处于某个压缩位置,跌落时动载荷大,而回弹行程受到系留索的限制,可能导致更大的反向载荷。可见,平台跌落时对起落架的冲击比着陆要严重得多。
业界对起落架动力学进行了广泛的理论和试验研究,主要目的是预估起落架与机身结构载荷,用于飞行器结构强度与疲劳寿命设计与评估[2]。文献[3]采用多体动力学模型,用经典方法可预估直升机着陆载荷;文献[4-6]采用刚-柔混合有限元模型计算着陆载荷及机体和起落架组件的应力;文献[7]利用流量系数计算法研究起落架减震器的性能及其对起落架跌落动力学的影响;文献[8]在全局有限元模型中改进了关键部位的有限元模型,研究粗暴着陆时关键部位的疲劳应力;文献[9]对全机进行着陆动力学仿真,研究着陆过程中起落架载荷及旋翼动力学行为。
升降平台跌落时的直升机受到冲击的原理与着陆一样,导致不同后果的主要原因是初始状态和约束条件不同,因此可以将直升机着陆动力学模型应用于平台跌落时的起落架过载计算。有研究表明,采用通用的动力学模型得到的起落架垂向载荷曲线与落振实验结果吻合[10]。鉴于此,本文将采用通用动力学模型仿真研究升降平台跌落对起落架过载的影响,为起落架及机体结构完整性评定提供载荷数据,更为升降平台制动系统的设计提供科学依据。
1 平台跌落时的起落架动力学模型
升降平台有匀速跌落和加速跌落等不同的跌落方式。直升机在平台上也有不同的系留方式[11],如机轮系留、机身系留等。假定采用机轮系留方式[12],即系留索一端与机轮的轮轴相连,另一端与升降平台相连,各个机轮用2 根系留索,系留索有预紧,但预紧力不大时可忽略其影响。若升降平台跌落时没有倾斜,不考虑直升机结构弹塑性,并且在跌落时结构没有发生破坏,那么升降平台跌落时,可单独建立起落架垂直方向的动力学方程。将缓冲支柱当成非线性弹簧S1、非线性阻尼器D1并联而成,也可将轮胎当成非线性弹簧S2和阻尼器D2并联而成,其力学模型如图1 所示。用起落架完全伸展且轮胎底面接触平台(或地面)状态,定义起落架相对于平台(跌落状态)或地面(着陆状态)的坐标系,缓冲支柱上部质量中心作为坐标z1的原点,轮轴中心作为坐标z2的原点。
设缓冲支柱以上的机体减缩质量为m1,位移为z1,缓冲支柱的压缩量为s1,弹性力为fs1,流体阻力为fd1,摩擦力为fμ。为兼顾着陆和跌落两种不同的情况,考虑旋翼拉力T 和平台跌落加速度a。若不考虑结构弹塑性,那么上部机体在相对坐标系中的垂直动力学方程为

图1 起落架力学模型Fig.1 Mechanical model of landing gear

设缓冲支柱下部和机轮组件的当量质量为m2,位移为z2,轮胎压缩量为s2,弹性力为fs2,阻尼力为fd2。系留索等效刚度为kT,与平台的夹角为β。当轮胎的压缩量大于其静止压缩量s20,即当Δs=s2-s20≥0 时,系留索松弛不起作用;反之当Δs <0 时,系留索张紧受拉,其弹性变形为sT。根据形变关系有sT=-Δs/sinβ。假定单个起落架的轮胎数量为nT,忽略机轮组件的摩擦力,机轮在相对坐标系中垂直方向的动力学方程如下
当Δs ≥0 时,有

当Δs <0 时,有

方程(1~3)为起落架动力学方程组。根据旋翼拉力T 和系留索刚度kT的不同取值,该运动方程组适用于着陆和跌落时的起落架动力学分析。着陆时无系留,可令系留索刚度为零,同时因地面固定不动,即平台加速度a=0;跌落时,可令旋翼拉力为零。
2 起落架力学模型
直升机着陆动力学计算时,缓冲支柱和轮胎的弹性力可根据其静压缩实验曲线获得。跌落动力学计算时,因跌落载荷可能超出静压缩实验范围,须建立缓冲支柱和轮胎静压缩性能的数学模型,使之适用于平台跌落时的起落架动力学分析。
起落架采用双腔式缓冲支柱,低压腔行程SL,充气压力为pL、气室活塞受压面积AL,与大气连通腔的活塞面积Aa;高压腔行程SH,充气压力为pH、受压面积AH。低压腔开始压缩前,刚度为ke的压缩弹簧首先伸展,当支柱压缩量达到s10后弹簧受到限动,而低压腔开始压缩;当支柱压缩量达到时s1cr时高压腔开始压缩。根据气体状态方程,可建立缓冲支柱压缩量与静载荷之间的关系如下
当0 ≤s1≤s10时,有

当s10≤s1≤s1cr时,有
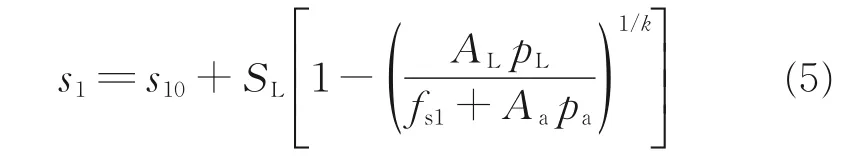
当s1>s1cr时,有

根据文献[13]中给出的模型参数辨识方法及辨识结果,得到缓冲支柱静压缩性能的理论和实验结果,如图2 所示。缓冲支柱动态变形时的弹性载荷与静压缩载荷有所不同,主要反映在气体多变指数k 具有不同值。

图2 缓冲支柱静压缩曲线Fig.2 Static compression curves of shock strut
文献[14]给出了轮胎力学模型,但轮胎大变形时其误差较大。本文用二次方曲线来拟合大变形时的力学特性,改进的轮胎力学模型如下
当s2≤10Czw/3 时,有

当s2>10Czw/3 时,有

式中:pr=0.25pb,pb表示轮胎最小爆炸压力;w 为轮胎宽度;d 为轮胎直径;Cz为载荷系数,本文Cz取0.03。
利用轮胎参数和现有的实验数据对模型参数进行识别后,得到轮胎静压缩性能的理论和实验结果,如图3 所示。应用该理论公式扩大了缓冲支柱和轮胎的载荷及变形范围,可用于平台跌落时机体结构破坏前的冲击载荷计算。
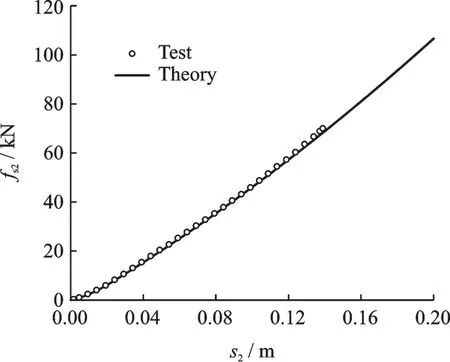
图3 轮胎静压缩曲线Fig.3 Static compression curves of tire
假定缓冲支柱活塞的承压面积为A0,压缩阻尼孔面积为As,回弹阻尼孔的面积为Ar,流量系数为Cd,油液密度为ρ。若不考虑温度影响,由流体力学经典的压力损失理论,得阻尼力与缓冲支柱内筒速度的关系为

根据文献[12],轮胎阻力为

式中CT为轮胎的当量阻尼系数,CT取0.1。
缓冲支柱内摩擦力包括动摩擦力和静摩擦力,按照文献[8]处理方法,将静摩擦力和动摩擦力合并在一起,表达式如下

式 中:μ 为 动 摩 擦 因 数;ε 为 一 临 界 值,这 里ε 取0.01 m/s。
起落架垂直方向的过载定义为起落架承受的垂向载荷与零升力停机载荷之比,垂向载荷是作用在起落架上垂直于地面的支反力,即

式中f0为零升力停机状态下的地面支反力。
在系留状态下,因系留索参与了受力,用地面支反力定义起落架过载无法反映出作用在机身上的载荷,因此不再适用。拟采用缓冲支柱载荷更为合适,此时起落架过载可定义为

式中fs0为停机状态下缓冲支柱载荷。
由于受机轮组件惯性的影响,按式(12,13)计算得到的起落架过载稍有差别,但最大过载的相对误差不会超过1%。为了对各种情况进行比较,本文均采用式(13)计算起落架过载。
3 起落架过载计算与分析
为比较着陆和升降平台跌落时的起落架过载,分着陆和平台跌落两种情况进行分析。因升降平台无倾斜垂直跌落时与直升机三点着陆相仿,因此本文对该状态进行过载计算与分析。
3.1 起落架着陆过载
直升机以机轮无滚动的三点着陆时,作用在单个主起落架上的机体的减缩质量m1=4 346 kg,机轮组件质量m2=2×40 kg,轮胎充气压力0.5 MPa。其余参数见文献[13]。着陆时旋翼拉力T=2(m1+m2)g/3。
对运动方程进行积分时,以轮胎底面触地时刻作为起始时间。根据坐标定义,此时质心和轮轴处的位移z1(0)= z2(0)=0 m,触地速度取着陆使用下沉 速 度vz0=ż1(0) =ż2(0) =1.83 m/s,得 到 起 落 架过载随时间的变化曲线,如图4 所示。

图4 起落架着陆过载Fig.4 Landing overload of landing gear
从图4 看到,起落架最大过载约1.24,低于该型直升机的使用过载2.67。缓冲支柱经第一个压缩-回弹周期,消耗了大部分着陆能量,一个压缩-回弹周期大约0.73 s,满足小于0.8 s 的设计要求。过载始终大于零,说明着陆时起落架始终没有跳离地面。
3.2 平台跌落时的起落架过载
为考察直升机在升降平台上系留对跌落载荷的影响,分无系留和机轮系留两种不同情形。考虑到系留索预紧力较小,在计算起落架停机载荷时忽略预紧力的影响,这样在停机载荷作用下起落架缓冲支柱和轮胎的压缩量可分别由静压缩曲线(图2、3)得到。在最大重量、重心中立位置时缓冲支柱的静压缩量理论计算结果为241.4 mm,轮胎的静压缩量为49.2 mm。停机状态缓冲支柱和轮胎的压缩量实测值如表1 所示,可以看出理论模型精度较高。

表1 停机状态缓冲支柱和轮胎压缩量Table 1 Static compression of shock strut and tire
3.2.1 无系留时平台自由跌落
假定直升机无系留,升降平台按规定速度匀速(0.2 m/s)下降,在某一高度突遇故障以自由加速度g 跌落。数值模拟中,缓冲支柱和轮胎的初始压缩量分别为s1(0)=0.241 4 m 和s2(0)=0.049 2 m,质心和轮轴处的初始位移分别为z1(0)=0.290 4 m 和z2(0)=0.049 2 m;起落架相对平台的初始速度vz0=(0) =(0)=0 m/s。为 了 与 着 陆 载 荷 比 较,将 平台的触地速度设为1.83 m/s。以故障发生时刻为起始时间,起落架过载如图5 所示,着陆载荷曲线也一并显示(虚线)。

图5 平台跌落时的起落架过载(无系留)Fig.5 Overload of landing gear while the platform dropping(not tied)
从图5 看到,升降平台跌落时起落架过载与着陆过载存在显著差异。平台自由跌落的时间不到0.2 s,在此过程中起落架过载迅速从1 降至0,说明自由跌落时缓冲支柱从静压缩状态迅速回弹,并且起落架有一个离开平台表面的过程短暂时间(0.15~0.17 s)。平台触地后,起落架最大过载2.14,约为着陆时的1.73 倍。
为更深入地理解造成两者显著差异的原因,从缓冲支柱的弹性力和阻尼力角度对着陆和平台跌落进行比较分析。因摩擦力相对较小,在此不做比较分析。缓冲支柱的弹性力和阻尼力曲线如图6表示。
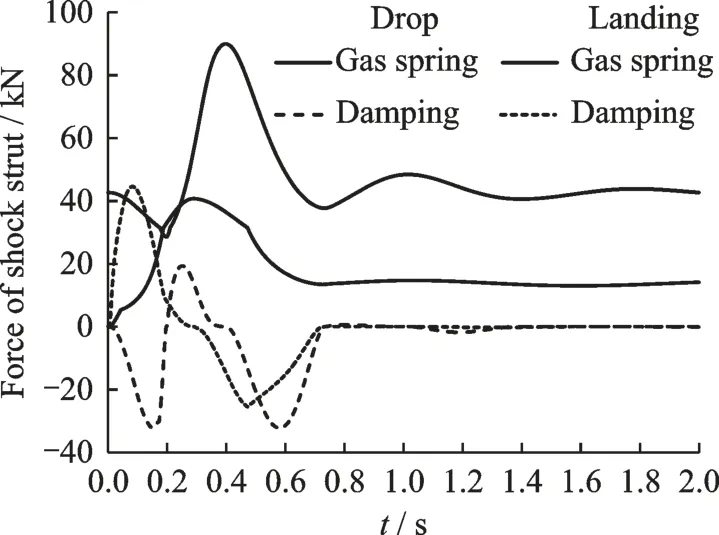
图6 缓冲支柱弹性力和阻尼力(无系留)Fig.6 Elastic and damping forces of shock strut(not tied)
从图6 中的曲线可看到,平台跌落时缓冲支柱的最大过载是由最大压缩量时的弹性力引起的,远高于着陆时的弹性力峰值。因为平台跌落时,缓冲支柱从静压缩状态回弹至某个压缩位置,接着在平台触地时缓冲支柱就开始受压,因此与着陆相比其起始刚度要大得多。又因缓冲支柱的非线性特性,随着压缩量的增加其刚度进一步增大,平台跌落状态下缓冲支柱的压缩时间更短、压缩量更小,若要吸收与着陆时相同的能量,相应地,弹性力也就更大。从阻尼力曲线可看到,因平台跌落过程中缓冲支柱迅速回弹,产生较大的反向阻尼力,而触地后缓冲支柱压缩过程中产生的阻尼力比着陆时小;然后在回弹时产生的反向阻尼力又比着陆时大。与着陆不同,平台自由跌落时,缓冲支柱的过载曲线没有出现动载荷峰值,过载峰值由弹性力引起。
平台从不同高度自由跌落时,起落架过载曲线如图7 所示。由图7 可知,跌落高度分别为0.168、0.30 和0.622 m(相应的触地速度为1.83、2.44 和3.5 m/s),起落架的最大过载分别为2.14、2.87 及4.11。可以得知,若升降平台的跌落高度超过0.6 m,起落架过载就已超过了设计过载4.0,说明即使直升机不系留,升降平台跌落时也会对直升机结构造成很大损伤。
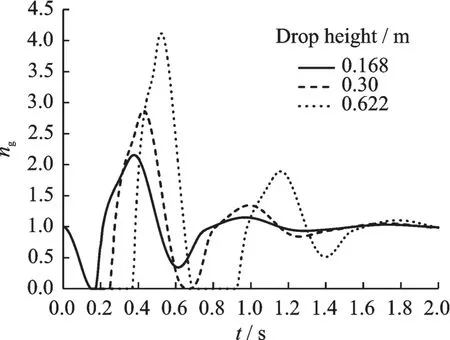
图7 不同高度自由跌落时的起落架过载(无系留)Fig.7 Dropping overload of landing gear from different heights(not tied)
3.2.2 机轮系留时平台自由跌落
机轮系留索具的预紧力可以调节,若预紧力不大,可忽略其对停机载荷的影响。跌落时轮胎受压缩时系留索松弛,回弹时因系留索的约束而限动,缓冲支柱则不受系留索的限动。设系留索等效刚度为107N/m,与平台表面的夹角为54°。当平台自由跌落时的触地速度为1.83 m/s 时,计算得到起落架过载的时间历程如图8 所示,同时显示了无系留时的起落架过载(实线)。

图8 平台自由跌落时起落架过载比较Fig.8 Comparison of overload of landing gear in free drop
从图8 看到,与无系留状态相比,平台跌落过程中,机轮系留的起落架过载下降得更快,平台触地后起落架压缩行程中的最大过载2.35,比无系留时大9.8%。究其原因,系留限制了机轮回弹,影响到了缓冲支柱的受载情况。在平台触地后缓冲支柱压缩回弹过程中,出现了一个时间极短、峰值很大的负过载,然后过载迅速恢复到初始状态,最大负过载达到-3.3,超过了最大压缩过载。为弄清这个现象,仍将缓冲支柱的弹性力和阻尼力分离出来进行分析,如图9 所示。

图9 平台自由跌落时缓冲支柱载荷比较Fig.9 Comparison of load of shock strut in free drop
从图9 看到,系留状态下缓冲支柱的阻尼力在0.45 s 左右呈现了“尖峰”,显然是在系留索张紧的瞬间出现的。由于轮胎在回弹过程中受到系留索的限动,其回弹速度瞬间降至零,与轮轴连接的缓冲支柱内筒速度也同样瞬间降至零,而缓冲支柱外筒并未受到系留索的限动,仍在空气弹簧的作用下继续伸展,使流经活塞阻尼孔的油液速度瞬间达到很大的值,造成阻尼力急剧增加,并迅速阻止外筒伸展。

图10 平台跌落时缓冲支柱的速度Fig.10 Speed of shock strut while the platform dropping
图10 显示缓冲支柱速度的时间历程。从图10可以看到,由于机轮系留的影响,在平台跌落阶段缓冲支柱的伸展速度增加得更快,平台触地时缓冲支柱的压缩速度也增加得更大;在缓冲支柱达到最大压缩后的伸展过程中,大约在0.45 s 时速度从-0.31 m/s 瞬间增大至-0.85 m/s,这显然是受到轮胎系留索的限动所致,接着支柱速度迅速减小后又缓慢降低至零值附近。
可以预见,跌落速度越大,起落架压缩时的正向过载及回弹时的反向过载将更大,如图11 所示。跌落高度分别为0.168、0.30 和0.622 m 时,起落架的最大正过载分别为2.35、3.01 及4.21,比无系留时分别大9.8%、4.9%和2.4%左右。最大负过载分别为-3.3、-7.0 及-14.7。这个结果说明,如果压缩行程其过载未导致结构破坏,那么在回弹行程结构将承受更大的过载而可能遭致破坏;若压缩行程的大过载已经导致结构破坏,那么动力学模型不再适用于回弹行程,也就不可能出现如此大的反向过载。
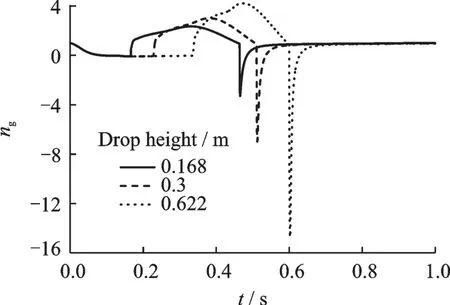
图11 平台以不同高度自由跌落时起落架过载Fig.11 Dropping overload of landing gear while the plat-form dropping from different heights
4 结 论
建立了升降平台跌落时的起落架动力学模型,仿真研究了机轮无系留和有系留时起落架过载,分析了平台跌落产生大过载的主要原因,得到如下结论:
(1)与着陆相比,升降平台跌落时起落架过载大得多,旋翼无升力及停机时起落架静压缩是造成大过载的主要原因。
(2)无系留情况下升降平台自由跌落时,如果平台的触地速度与直升机着陆速度同为1.83 m/s,那么跌落时起落架的最大过载是着陆过载的1.73 倍。
(3)升降平台以不同高度自由跌落时,机轮系留情况下起落架的最大正过载高于无系留时的起落架过载,但相对增加量在10%以内。
(4)升降平台自由跌落时,机轮系留会引起起落架产生很大的负过载,其值高于缓冲支柱压缩时的最大正过载。跌落高度越高,这个效应越显著。

