结构参数对纱线及织物芯吸性能影响的研究进展
王丽莉,刘 宇,徐天骄
(上海市质量监督检验技术研究院,上海200040)
0 引言
纺织品在人们的日常生活中十分常见,尤其服用纺织品,它可以用来维护人体和外部环境间的热湿平衡,以满足生存需要。随着科学技术的快速发展和经济的提升,人们对物质文化的需求不断提高,更加注重服装的服用舒适性。基于这一点,国内外很多科研人员对于纱线、织物中的液态水的传递一直都在不断研究中。在织物中,液态水的运输是影响服装舒适性的关键因素。织物通过把水从皮肤表面迅速运输到外界环境,使皮肤表面保持干燥,让着装者感觉更加舒适。因此,改善纤维及其面料的服用舒适性与功能性,充分挖掘纤维的优良性能,使之为人们所使用,已经成为纺织行业的一个重要研究方向。
1 芯吸效应理论分析
液体通过毛细管压力驱使自发运输到多孔系统的过程被称为芯吸。在毛细管系统中,芯吸过程可看成固液界面取代固气界面的自发过程[1]。纺织织物或纤维的芯吸是指水分子沿着纤维表面间所形成的毛细管道运输到一定高度的性能。在毛细管内,液体的自然流动和伴随液体扩散进入纤维内部或纤维膜的自然流动是芯吸运动的两种运动过程[2-3],而本文的研究对象是第一种芯吸运动。
在纱线内利用纤维间形成的毛细管来传递液体以完成纱线的芯吸,固体间产生毛细管效应需要具备两个条件[4-5],即:液体能附着在固体表面,或者说是能够润湿固体表面;纤维与纤维之间形成足够小的毛细管,水分在此毛细管内表面呈内凹的弯月形曲面,这种内凹的弯月面存在一个附加压强PS,可用公式(1)表示。

式中:∂——水分的表面张力系数,N/m;
R——弯月面的曲率半径,m。
当毛细管壁被毛细管中的流体湿润了,管内形成了一个弯月形曲面,液气界面的张力附加到液柱上,根据Laplace方程[1],毛细管压力差可用公式(2)表示。
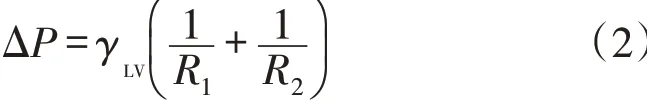
式中:ΔP——毛细管压力差,Pa;
γLV——液气界面张力,N/m;
R1、R2——两个弯曲面轴向的曲率半径,m。
对于圆形截面毛细管,当毛细管壁完全被液体湿润时,液气界面可假设为一个半球形,两个弯曲面的曲率半径R1=R2=R,此时毛细管压力差可用公式(3)表示,即:

当毛细管壁未被液体完全湿润时,会形成一个接触角θ(固液接触角),可用公式(4)表示。

式中:r——是毛细管当量半径,m。
式(3)就变为:
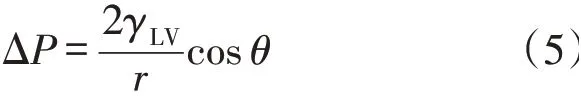
由于毛细管压力为正,因此接触角θ在0°~90°。此外,毛细芯吸的差动效应引起毛细管芯吸过程往往具有方向性,会由大半径孔隙向小半径孔隙流动[6]。
另外,根据Poiseulle方程,液体的毛细流速q(单位时间的流量)为:
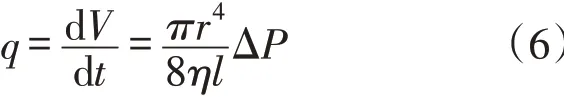
单位时间内的线速度v为:
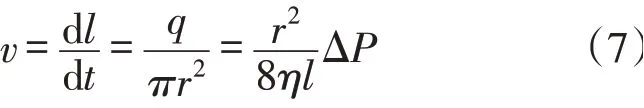
基于Poiseulle方程,在不考虑重力的情况下,Lucas-Washburn导出毛细管的流速方程[1,7]为:
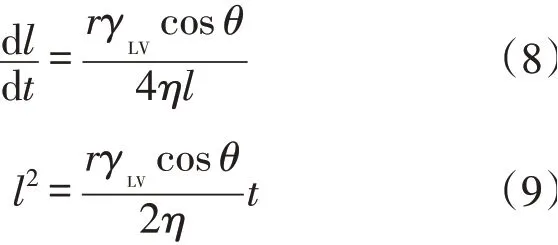
式中:l——毛细管吸水长度,m;
η——液体黏度,Pa·s;
V——液体体积,m3
综合上述分析可知,液气界面张力、纤维的吸湿性、纤维集合体内的毛细管大小和液体的黏度都对液体的芯吸速度有着较大的影响[8]。因此,要使得液体能以较快的速度上升到较高的高度,就必须要求毛细管有一个合适的半径值[4]。
2 国内外芯吸性能研究进展及现状
由于纱线和织物内部导水情况以及其相应的原理极为复杂,即使历经多年,研究者们对芯吸影响因素和优化服装舒适性的研究也一直未有中断。为了更好地了解芯吸性能的研究进展,本文主要从理论模型、试验研究、数值模拟等3个方面进行介绍和分析。
2.1 芯吸性能理论模型的研究进展
Amico S等[9-10]提出并构建了关于微观孔隙和宏观孔隙的双尺度流体理论模型,预测渗透长度与时间、表观渗透率、毛细压力等的函数关系,通过一系列织物芯吸试验研究双尺度上的芯吸现象,验证试验数据和理论预测的相关性。施楣梧等[11]提出了织物湿传导的3种通道模型,并指出织物中多层次结构的透湿孔洞因其横向尺寸的不同而导致孔隙对织物导湿的作用存在差异。王其等[12-15]提出3个层次的导湿结构模型,并对应构建了其中的高导湿纱线模型和导湿织物模型,发现织物里外层纤维的特性、线密度、根数以及织物里外层的厚度均会影响导湿模型的快干功能,从而提出优化纱线和织物结构参数以达到导湿快干效果的结论。Bravo等[16]在两相流的应用中利用达西定律对Washburn模型进行完善,获得多孔介质中毛细上升高度与时间之间的关系表达式。Shou等[17-20]构建了不同孔长度、宽度和孔隙率等情况下上下层多孔结构模型,在毛细压力和渗透率交互作用前提下对液态吸水情况进行研究探索,并通过优化孔隙结构得到最小的吸收时间,这一发现在很多领域中对关于水处理的多孔设计具有重要的指导价值。
以往诸多学者均利用Lucas-Washburn方程法,在假设纱线内部纤维间的孔隙为光滑毛细管的前提下,对纱线的导水机制问题进行研究[21]。但在后来的研究与实际生产应用中,研究人员发现对不均匀毛细管的研究更具有实际应用价值,纱线内的微观孔隙和织物内的宏观孔隙的大小以及孔隙连续性影响着纱线和织物芯吸导水的速率,对理论模型不断优化。
2.2 芯吸性能的试验研究进展
人们对芯吸性能的试验测试方法一直在不断的优化中。目前,依据试验机制和相应的表征方式可将试验方法分为3类,即:垂直芯吸法、液滴扩散法和称重法,其中垂直芯吸法是纱线和织物芯吸性测试中最常用的方法,常用试验装置详见图1。
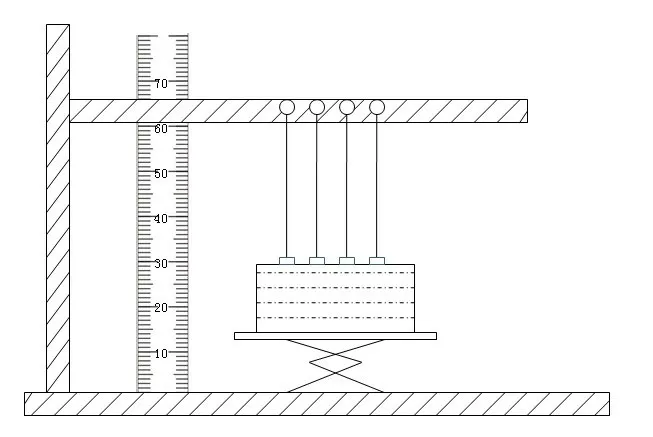
图1 垂直芯吸试验装置图
Reed等[22-25]通过推导垂直芯吸模型的平衡物理公式,对纤维集合体内的液体传输机制进行研究,发现对液体芯吸行为影响较大的因素包括纤维材料自身吸湿性能、纤维直径、纱线的形状及加捻程度等。查安霞等[3-4,26-27]分析了芯吸效应的形成机制,通过芯吸试验初步探讨了不同截面、纱线加捻程度、单丝纤度、针织物稀密程度、未充满系数和织物组织结构等因素对芯吸的影响,从而确认了影响芯吸的相关因素,并通过控制上述诸多因素设计出利于芯吸的舒适面料。李毅等[28-29]对加捻纱进行垂直芯吸试验,研究了张力大小和纱线捻度对纱线芯吸性能的影响。詹永娟[30]使用LED光源对织物内液态水的垂直传输性能进行了处理,并辅以软件进行拟合芯吸速率,通过灰色关联分析法对棉机织物内液态水的垂直传输性能影响因素进行探讨。通过多次试验研究,发现影响纱线及其织物芯吸效应的因素涉及纤维的形状、单丝细度、纱线的加捻程度、织物的组织结构、织物紧度等多个方面。对于服装设计来说,服装材料的选择及加工处理对服装服用舒适性有着直接性的影响。通过综合考虑上述多因素的影响,设计出有利于提高芯吸性能的面料,为改善服装服用舒适性起到至关重要的作用。
2.3 芯吸性能的数值模拟研究进展
Pillai[31-32]使用软件构建织物的简单模型,用软件进行流体模拟,分析织物的液态水传递原理和纱线间距、纱线直径、孔隙尺寸及分布等方面与多孔介质中水分蒸发的关系,为优化多孔材料提供设计依据。张艳等[2]构建纤维束单元模型MFB和纤维束截面随机排列模拟系统Shape-Generator,通过计算机进行模拟,研究了芯吸效应的影响因素。朱娜[33]建立仿生织物模型,通过FLUENT软件模拟分析了织物和纱线内部的液态水传输过程。王丽莉[34]通过建立纱线和织物内纤维间孔隙的物理模型,用FLUENT软件模拟纱线织物内液态水在不同孔隙结构情况下的运动趋势,进而研究不同孔隙结构参数对纱线织物的芯吸影响。齐园园[35]建立了二维、三维藕节管模型,使用FLUENT仿真研究纳米纤维包覆长丝纱的芯吸导水过程,进而研究不同孔隙结构参数对纱线的芯吸影响。耿长军[36]建立了“钥匙形”分级孔隙结构模型,并通过层流方法进行模拟,验证了该孔隙结构模型的导水性能和吸水扩散能力。运用CFD仿真模拟方法模拟结构复杂的纺织材料导水性能,可减少数学理论求解纺织品导水性能的复杂性,且模拟结果具有良好的可靠性和可行性,作为一种有效的研究织物服用舒适性的方法,值得深入研究。
2.4 纱线及织物芯吸性能研究中存在的问题
研究纱线的导水性能通常使用理论模型和试验测量的方法,但由于实际纱线和织物导水过程的复杂性,这两种方法并不能直观表征液体在织物纱线内部的流动情况。使用CFD数值方法可以形象地表达出液态水在纱线和织物中流动的速度指标,对研究织物服用舒适性具有重要的指导意义。然而,对于液态水在纱线织物中的运动数值模拟研究还有许多问题有待进一步解决,主要涉及的问题为:构建织物的几何模型太简单,不能如实反映织物的形态结构以及纱线的屈曲状态;构建复杂的织物内传输液态水的模型,求解起来较困难;用CFD技术从纤维、纱线、织物的结构参数方面入手,系统分析液态水在织物中传输的相关研究很少。
3 结论
(1)纤维间的毛细孔隙是决定纤维材料导湿性能的主体,对纺织面料的湿舒适性具有重要的影响。研究人员一直在对纱线和织物的芯吸方法创新研究,通过理论模型研究、试验设计、CFD模拟方法等不断探索中。
(2)影响纱线以及织物芯吸性能的因素较多,其中纤维的形状、纱线加捻程度、单丝细度、织物经纬纱交织产生的交互作用以及其他结构参数对纱线和织物水分传递行为特征有着重要的影响。将理论模型研究、试验设计、CFD模拟方法等相结合,可更方便、准确地优化提高纺织品导水性能结构参数,为今后舒适性纺织品的发展提供新的开发方向。
(3)使用CFD数值模拟的方法可形象地表达出液态水在纱线织物中的流动速度指标,优化结构参数,对研究织物服用舒适性具有重要的指导意义。然而,数值模拟还存在不少难题,比如:模型构建简单、复杂的模型求解难、相关CFD模拟文献研究少等。要解决这些问题需要强大的系统软件来支持,更需要研究人员进一步从纤维、纱线、织物的物理性能和结构参数方面入手,加大对液态水在织物中传输的相关研究。

