具有体积分数梯度的连通装置甲烷-空气爆炸特性数值模拟*

许晓元，孙金华，刘晅亚

（1. 中国科学技术大学，安徽 合肥 230026；2. 应急管理部天津消防研究所，天津 300381）

含有可燃气体的连通型装置在现实中普遍存在。可燃气体通常在密封的封闭空间中，如反应器、反应釜、储罐等各类化工容器或生产装置，这些装置之间并不孤立，而是经由管道连接形成连通型装置。可燃气体在生产、储存、运输和使用过程中由于人为失误、容器和管道的缺陷、外部环境等因素，导致容器管道封闭空间内混入空气等其他助燃性气体，极易发生爆炸。经过前人研究，连通装置爆炸强度比单一容器更高，这是因为爆炸波和燃烧火焰通过管道传播，会导致气体的压缩并使得气体湍流程度更高。研究表明，当连通型装置间的管道较长时，长、径比超过40，爆燃就有可能在管道内演变为爆轰，此时爆炸传播速度可达2 000 m/s，压力达到甚至超过3 MPa。除连通型工艺装置外，实际生产活动中也存在多种形式的连通型结构。如建筑物中畅通的两个或多个房间，矿井中的空间及通道，核电保护装置与冷却循环装置等。这些连通型装置内部都有可能发生危害性极大的可燃气体爆炸事故。在实际生产装置爆炸事故中，由于管道较长、装置结构复杂，因此，发生可燃气体与主燃气体混合过程中，可燃气体混合物在装置内分布不均匀，存在体积分数梯度。另外，煤矿井下通风不畅、密闭的隧道中瓦斯也存在体积分数梯度。因此，研究具有体积分数梯度的连通装置的可燃气体爆炸特性对指导爆炸防控工作更具有实际意义。

针对连通装置内可燃气体爆炸特性和泄爆技术的研究，国内外学者做了大量的研究，前人针对连通装置爆炸的绝大多数研究都基于连通装置内的气体为均一体积分数，前人的研究主要集中在爆炸危害后果、爆炸影响因素和泄爆技术几个方面。连通装置可燃气体爆炸的影响因素主要为尺寸效应（容器容积比例、管道的长度、管径的大小等）、点火位置、火焰传播方向、障碍物阻塞率和位置等。在连通装置爆炸危害后果研究方面，Bartkneckt[1]指出，当连通装置两个容器的容积比为1∶1 时，与独立容器相比压力上升速率提高了10 倍，压力上升速率增高的原因是气体湍流和喷射火焰；Phylakton 等[2]研究发现，连通装置的爆炸强度及压力上升速率与燃烧速度关系密切，而燃烧速度又与湍流程度相关，通过测定，连通装置内最大燃烧速度可达370 m/s，最大压力上升速率可达2.086×108Pa/s。在连通装置爆炸影响因素研究方面，Lunn 等[3]通过粉尘爆炸实验研究了连通装置容积比及连接管径的影响，研究表明，管道体积与容积体积之间的比例也是影响燃烧爆炸的因素之一；Holbrow 等[4]针对连通装置的粉尘爆炸做了大量试验研究，可燃物质采用煤粉、石墨粉等，实验发现，管道长度、直径、容器容积比、粉尘的燃爆性能和泄放面积均对爆炸压力有很大影响；Holbrow 等[5]开展了实验研究，实验装置为容积为2～20 m3的圆柱形容器，管道长15 m、半径分别为0.15、0.25、0.50 m 的管道容器组合的连通装置，研究了容积比例、管径、泄爆面积等因素对连通装置内粉尘爆炸和泄爆的影响；严建骏等[6]、尤明伟等[7]、王志荣等[8]采用实验方法研究了连通装置内气体爆炸过程，主要从初始条件、点火位置、火焰传播方向来分析连通容器内压力变化；尤明伟等[9]分析了障碍物阻塞率和位置、连接管道直径和长度、火焰传播方向、点火位置等因素对火焰传播及爆炸强度的影响。在连通装置泄爆方面，王志荣等[10]研究了连通装置内气体的泄爆，结果表明一个泄爆口不能明显降低容器内的超压，而两个泄压口同时泄爆才能更好地实现泄爆。

学者们在研究中将体积分数梯度方向与爆炸波传播方向垂直的情形定义为垂直体积分数梯度，将体积分数梯度方向与爆炸波传播方向平行的情形定义为平行体积分数梯度，见图1。前人的体积分数梯度气体爆炸研究主要用的方法为实验研究和数值模拟研究，研究的对象大多为单一容器或管道。在受限空间内平行体积分数梯度爆炸研究方面，Thomas 等[11]在22 mm×10 mm×500 mm 的受限空间及直径为50 mm 的爆轰管内研究了平行体积分数梯度对爆炸传播速度的影响；Kuznetsov 等[12]在内径为174 mm 长度为6.0～11.2 m 的爆轰管研究了氢气-空气平行体积分数梯度对爆轰波的影响，探讨爆轰波熄灭、二次起爆、爆燃转爆轰等动力学行为。在受限空间内垂直体积分数梯度爆炸研究方面，Vollmer 等[13-14]研究了截面60 mm×300 mm长5.4 m 的管道内氢气-空气垂直体积分数梯度、障碍物等对氢气-空气火焰加速、爆燃转爆轰距离的影响；Kessler 等[15]研究了垂直体积分数梯度中爆炸波的稳定性和淬火概率问题；Ishii 等[16]在截面40 mm×20 mm 长0.5 m 的管道内研究了垂直体积分数梯度如何影响爆轰波阵面形状和爆轰不稳定性；Wang 等[17]对前人的实验开展了数值模拟，对氢气爆炸和丙烷爆炸流场进行研究；Han 等[18]利用数值模拟的方法研究了垂直体积分数梯度对爆轰波前沿结构稳定性的影响。

综上所述，封闭空间具有体积分数梯度的可燃气体爆炸研究，由于其与实际工程问题最接近，且通过研究能解释实际工程问题所面临的难点，更为重要的是非均匀气体爆炸所涉及的火焰加速、爆燃转爆轰、爆轰波传播机理与均匀气体存在较大的差别，近年来逐渐成为国外学者的研究热点，而针对连通装置内体积分数梯度的爆炸研究还鲜有报道。本文中将通过数值模拟的方法研究连通装置内均一体积分数和具有体积分数梯度的CH4爆炸过程中的爆炸参数、爆炸波传播等特点，以期为连通装置内可燃气体爆炸事故防控、泄爆技术提供理论指导。

图1 体积分数梯度分类Fig.1 Volume fraction gradient classification

1 数值模拟研究

1.1 物理模型模拟软件及工况设置介绍

选取容器管道连通装置作为研究对象，研究具有体积分数梯度的容器管道连通装置内甲烷气体爆炸特性。该装置由两个圆柱形爆炸容器通过方形管道连通，水平布置在地面上，见图2。大容器的容积为60 L，小容器的容积为20 L，两个容器直径与容器高度之比为1∶1，在大小容器底部由一个截面积为0.035 m×0.035 m，长为3 m 的方形管道连接。为了研究体积分数梯度，将连通装置划分为5 个区域，区域1 为大容器，区域2 为连接大容器的长为1 m 的管道1，区域3 为连接管道1 的长为1 m 的管道2，区域4 为连接管道2 和小容器的长为1 m 的管道3，区域5 为小容器。

本文中将容积总计83.7 L 的连通装置划分为156244 个非结构化网格，网格划分情况见图3。可燃气体初始条件设置：压力为105Pa，温度为300 K，爆炸容器的壁面设置为粗糙的绝热壁面。本研究中做了网格无关化分析，当网格划分为18 348 个非结构化网格时，某一工况条件下连通装置爆炸的最大压力为665.5 kPa，当网格划分为85 648 个非结构化网格时，相同工况条件下连通装置爆炸的最大压力为680.2 kPa，当网格划分为156 244 个非结构化网格时，相同工况条件下连通装置爆炸的最大压力为676.9 kPa，粗糙网格、中等网格与精密网格压力值的误差分别为−1.68%和0.488%，误差较小，可知三种网格划分情况对结果的影响很小，因此，本研究所有工况的网格设置为156 244 个非结构化网格。为了验证Fluidyn 软件对爆炸模拟的可靠性，本文利用本软件模拟了文献[19]中同工况条件9.5%甲烷爆炸的实验，物理模型的对比图见图4，根据实验工况将数值模拟中爆炸容器壁面设置为传热时，通过分析结果可知，数值模拟的结果比实验值高7.10%，偏差可以接受。由于当壁面假设为绝热时，爆炸危害后果最严重，因此，本文所有的研究中均将壁面设置为绝热条件。

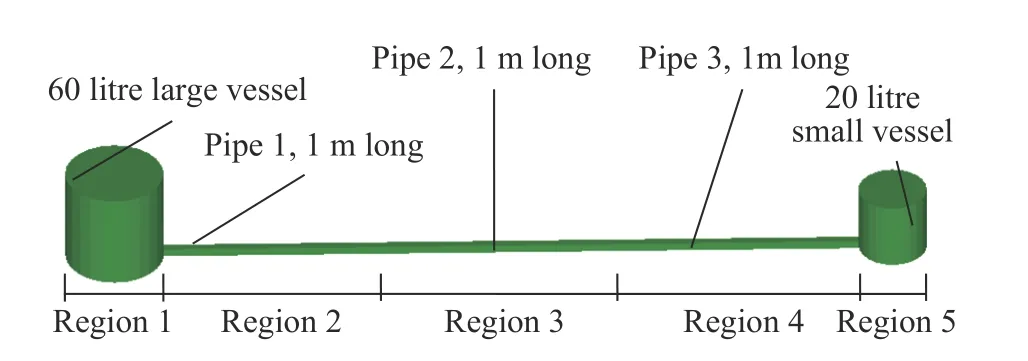
图2 管道容器连通装置Fig.2 A connection device with pipes and vessels

数值模拟软件Fluidyn 求解Navier-Stokes 方程以及描述理想气体混合物的物种体积分数、质量和能量守恒的方程。求解紊流方程的雷诺平均，雷诺应力采用线性涡黏模型（LEVM）进行建模。控制方程如下：

式中： ρ 为密度，U 为速度矢量，ym为物质m 的质量分数，t 为温度，Dm为物质m 的有效扩散系数，Sm为物质m 方程的源项 m =1,···,n。

Fluidyn 中线性涡黏性模型为：

图3 网格划分Fig.3 Model mesh generation

图4 实验装置和物理模型的比较Fig.4 Comparison between the experimental apparatus and the physical model

式中：Γ 为输运系数，下标l 表示依赖于流体的层流（分子）成分；下标t 表示湍流成分。

数值模拟软件Fluidyn 中湍流模型运用的为k-ε 模型，k-ε 模型是一个双方程线性涡黏性模型。Fluidyn CFD 求解器在三维空间和时间上求解的控制方程可以表示为一般对流扩散方程，其形式如下：

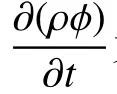
数值模拟软件Fluidyn 中爆炸模型的化学反应流模型包含Arrhenius 化学动力学模型和涡流耗散模型。在Arrhenius 模型中，反应速率用 Kj表示，涡流耗散模型中，反应速率用 K 表示。Kj完全由化学动力学决定。Arrhenius 形式如下：

式中：Aj为指数前因子，T 为热力学温度，ζj为温度指数，Ej为活化能，R 为通用气体常数， xi为物质 i 的摩尔分数，vi为物种 i 速率指数。

Arrhenius 模型只考虑了反应的化学动力学部分，但没有考虑湍流对反应速率的影响。由于湍流微混合，瞬时体积分数变化很大。数值模拟软件Fluidyn 建立了以燃料和氧化剂为反应物的燃烧反应的涡流耗散模型。在该模型中，反应速率计算如下：

式中：k 为湍流动能，ε 为湍流耗散率， ρ 为密度，Mf为燃料分子量，Aedc、Bedc为常数，yf为燃料质量分数，yo为氧化剂质量分数， yp为产物质量分数， φo为氧化剂燃料比，φp产物燃料比。

利用Fluidyn 软件来对具有体积分数梯度的容器管道连通装置进行研究，设置的工况见表1。CH4的可爆体积分数区间为5.0%～15.0%，本文研究了整个连通装置内CH4体积分数均在爆炸区间内的情形，为保证CH4的爆炸反应，将CH4的体积分数取为6.0%～14.0%。区域1 的体积分数保持6.0%不变，其他各区域体积分数按一定数值依次增高。将体积分数梯度定义为区域5 的体积分数值减去区域1的体积分数值。本文中研究了体积分数梯度分别为2.0%、4.0%、6.0%、6.5%、7.0%、7.5%、8.0%的工况。将具有体积分数梯度的工况时，连通装置内平均CH4体积分数作为此体积分数梯度工况的均一体积分数对比工况，通过计算，体积分数梯度为2.0%、4.0%、6.0%、6.5%、7.0%、7.5%、8.0%对应的均一体积分数分别为6.517%、7.034%、7.551%、7.697%、7.827%、7.958%、8.067%。所有工况中，点火位置位于区域1 即大容器的中心。为研究不同工况下的爆炸压力等参数，在每个区域的中心位置设置测点，该测点可测量压力、温度、速度。

表1 模拟工况Table 1 Simulated working conditions

1.2 体积分数梯度对连通装置内最大压力的影响

对不同工况条件下最大爆炸压力、最大爆炸压力所处的位置、达到最大爆炸压力时刻进行分析，见表2 和表3，表2 为连通装置不同体积分数时最大爆炸压力情况，表3 为连通装置不同体积分数梯度时最大爆炸压力情况。通过分析表2 和表3 可知，连通装置内均一体积分数为6.517%～8.067%及区域1 体积分数6.0%体积分数梯度为2.0%～8.0%，且区域1 中心点火时，最大爆炸压力位于区域5。由于大容器作为起爆容器，小容器作为传爆容器，爆炸激波从大容器经管道的持续加速传播至小容器，小容器内的气体受到挤压并产生强烈化学反应，因此导致小容器的爆炸压力最大。

图5 为不同工况条件下最大爆炸压力随体积分数/体积分数梯度变化曲线图。通过图5 可知，连通装置最大爆炸压力随均一体积分数的增大而增大，约成线性关系；连通装置最大爆炸压力随体积分数梯度的变化不是线性关系，最大爆炸压力与体积分数梯度的变化曲线出现2 个波峰，一个是4.0%一个是7.0%。这是因为CH4与O2的化学反应当量比时C H4的空气体积分数为9.5%[20]，均一体积分数越接近当量体积分数，爆炸压力越大。当体积分数梯度为2.0%～7.0%时，所对应的工况比相应工况最大爆炸压力大，即具有体积分数梯度所发生爆炸危害后果更严重。当体积分数梯度为7.5%～8.0%时，所对应的工况比相应工况的最大爆炸压力小，即均一体积分数工况发生爆炸危害后果更严重。从图5可以推断，在体积分数梯度7.0%～7.5%之间，存在一个体积分数梯度值，在此体积分数梯度情况下，所对应的工况与相应工况所产生的效果一致。由于工况11 和工况13 的体积分数与化学当量比较接近，化学反应完全，释放的能量大，因此这种情况下，均一体积分数比具有体积分数梯度的工况产生的最大爆炸压力大；工况1、3、5、7、9 的体积分数与化学当量比差距较大，而工况2、4、6、8、10 中，连通装置的部分区域的体积分数与CH4化学当量比体积分数较为接近，因此这种情况下，体积分数梯度比均一体积分数工况所产生的最大爆炸压力大。图6 所示为不同工况条件下最大压力时刻随体积分数/体积分数梯度的变化。由图6 可知，最大压力时刻随体积分数的增大而提前，并约成线性关系；而最大压力时刻值随体积分数梯度的增大先提前再滞后。这是因为，在6.517%～8.067%范围内，随着体积分数的增大，越来越接近CH4的化学当量体积分数，越接近化学当量体积分数，爆炸反应越快，因此，达到最大爆炸压力最大值的时刻越提前。

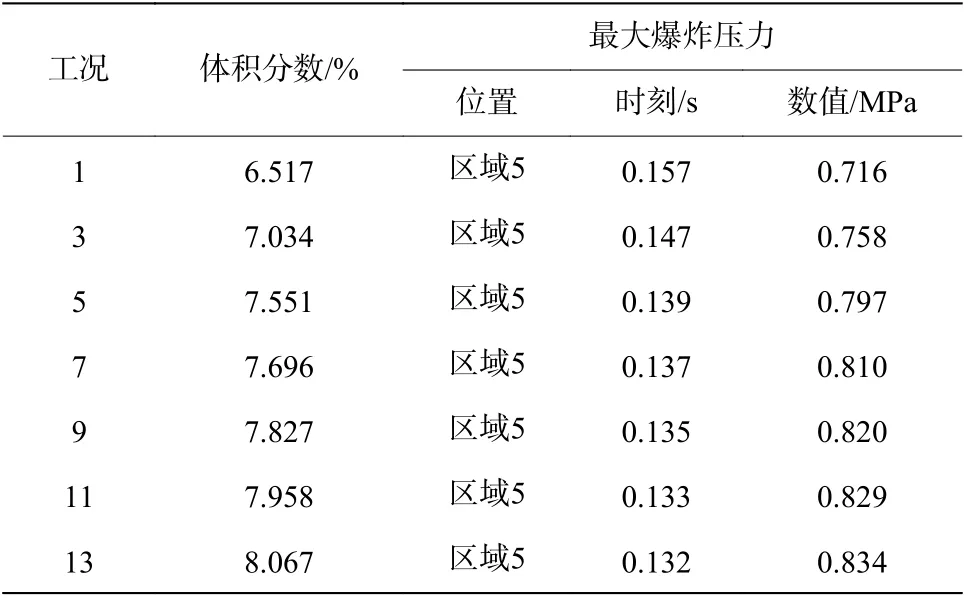
表2 连通装置不同体积分数时最大爆炸压力相关参数Table 2 Related parameters of the maximum explosion pressures for different volume fractions of connected devices

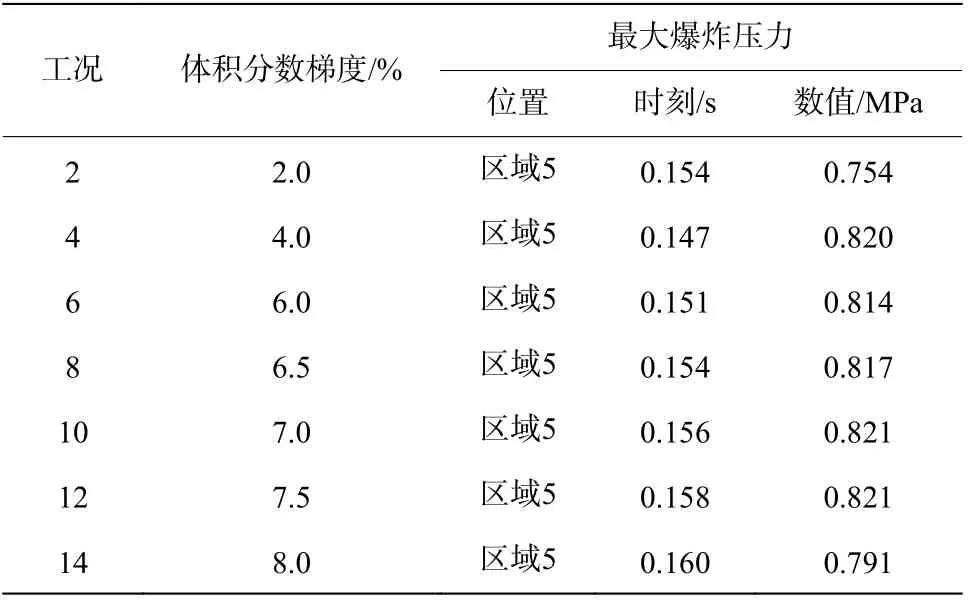
表3 连通装置不同体积分数梯度时最大爆炸压力相关参数Table 3 Related parameters of the maximum explosion pressures for different volume fraction gradients of connected devices

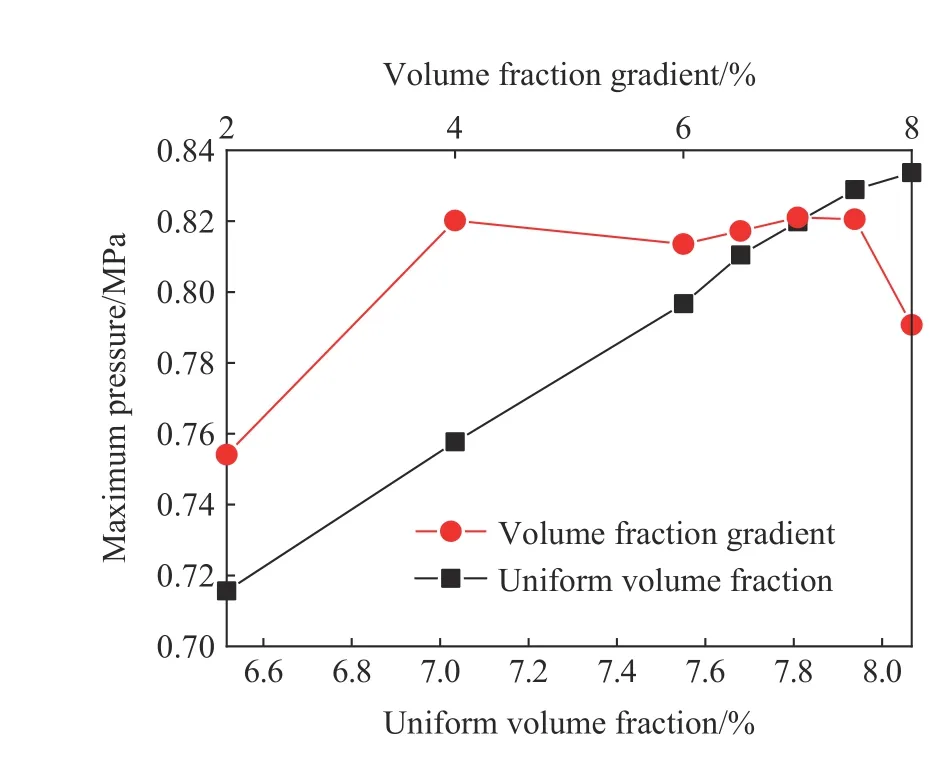
图5 不同工况条件下最大爆炸压力随体积分数和体积分数梯度变化曲线Fig.5 Changes of the maximum explosion pressure with volume fraction and volume fraction gradient under different working conditions

1.3 体积分数梯度对连通装置内最大压力上升速率的影响

对不同工况条件下最大压力上升速率、最大压力速率所处的位置、达到最大压力上升速率时刻进行了分析，见表4 和表5，表4 为连通装置不同体积分数时最大压力上升速率情况，表5 为连通装置不同体积分数梯度时最大压力上升速率情况。通过分析表4 和表5 可知，连通装置内均一体积分数为6.517%～8.067%及区域1 体积分数6.0%体积分数梯度为2.0%～8.0%，且区域1 中心点火时，最大压力上升速率位于区域2 或区域3。这是因为，压力上升速率代表着爆炸气流的湍流程度，爆炸压力波从区域1 传播至区域2，空间骤然变小，导致爆炸气流湍流程度增强，因此，区域2 附近的管道位置压力上升速率最大。

图7 所示为不同工况条件下最大压力上升速率随体积分数/体积分数梯度变化曲线。通过图7 可知，连通装置最大压力上升速率随均一体积分数的增大而增大，约成线性关系；连通装置最大压力上升速率随体积分数梯度的变化不是线性关系，最大压力上升速率与体积分数梯度的变化曲线出现2 个波峰，一个是4.0% 一个是7.5%。这是因为均一体积分数越接近当量比体积分数，爆炸越剧烈，最大压力上升速率也越大。当体积分数梯度为2.0%～4.0%时，体积分数梯度工况比对应的均一体积分数工况最大压力上升速率大，当体积分数梯度为6.0%～8.0%时，体积分数梯度工况比对应的均一体积分数工况最大压力上升速率小。从图7可以推断，在体积分数梯度4.0%～6.0%之间，存在一个体积分数梯度值，在此体积分数梯度情况下，爆炸的最大湍流程度与对应的均一体积分数工况一致。图8所示为不同工况条件下最大压力上升速率时刻随体积分数/体积分数梯度的变化。由图8 可知，最大压力上升速率时刻随体积分数的增大而提前，并约成线性关系；而最大压力上升速率时刻随体积分数梯度的增大先提前再滞后。这是因为，最大压力上升速率存在于压力快速上升即爆炸的过程中，在6.517%～8.067%范围内，随着体积分数的增大，越来越接近CH4的化学当量体积分数，越接近化学当量体积分数，爆炸反应越快，因此，达到最大压力上升速率最大值的时刻越提前。

表4 连通装置不同体积分数时最大压力上升速率相关参数Table 4 Related parameters of the maximum pressure rise rates for different volume fractions of connected devices

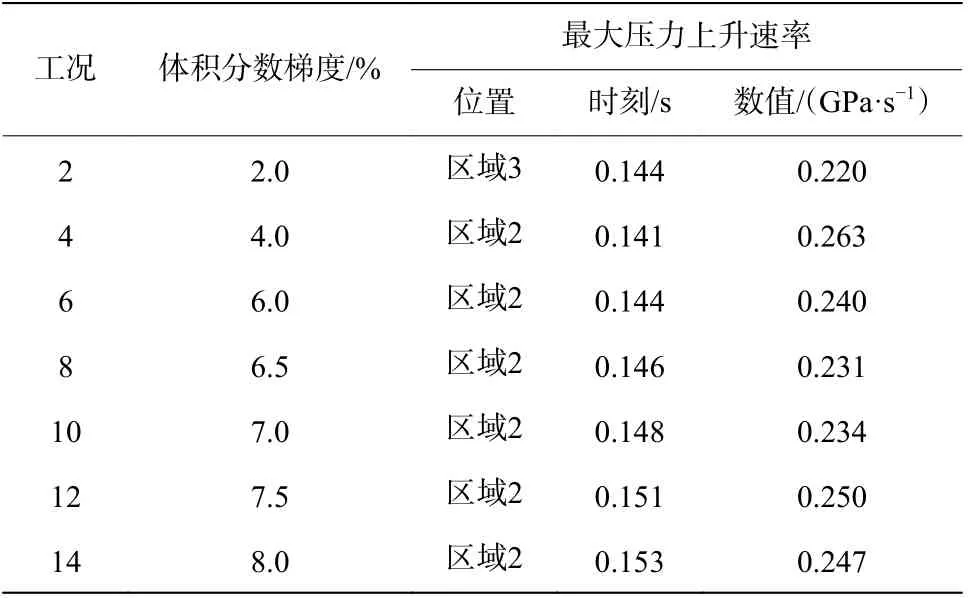
表5 连通装置不同体积分数梯度时最大压力上升速率相关参数Table 5 Parameters related to the maximum pressure rise rates in the connected devices with different volume fraction gradients

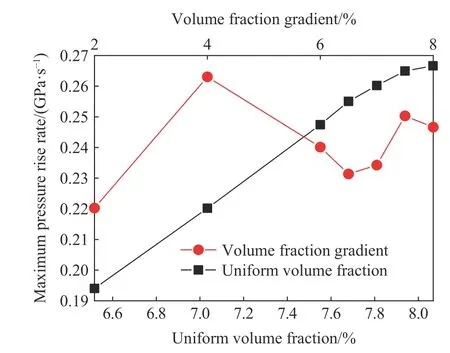
图7 不同工况下最大压力上升速率随体积分数和体积分数梯度的变化Fig.7 Changes of the maximum pressure rise rate with volume fraction and volume fraction gradient under different working conditions

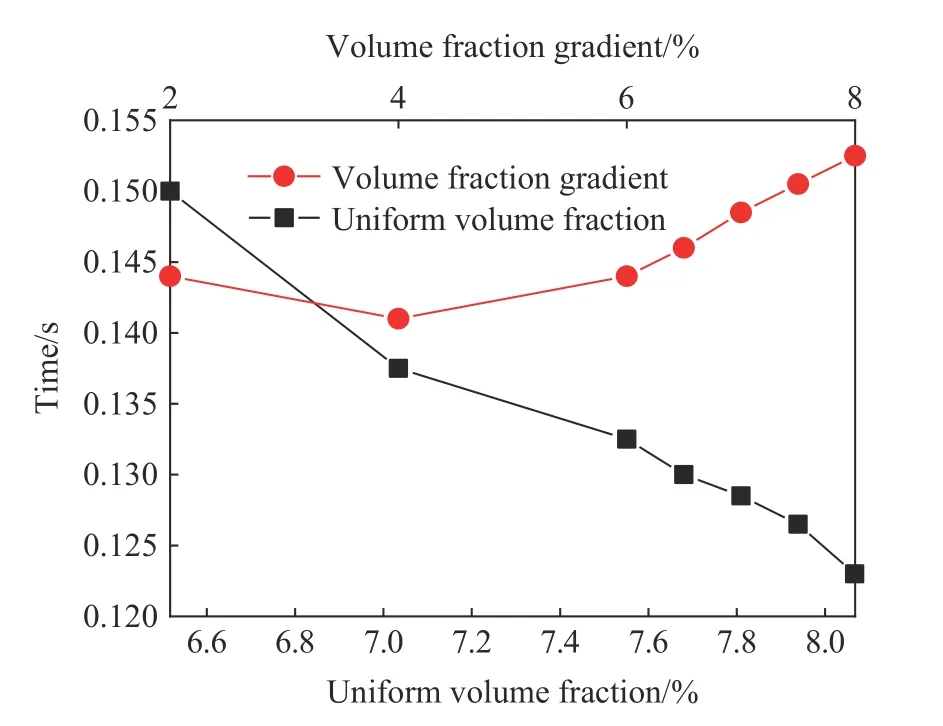
图8 不同工况下最大压力上升速率时刻随体积分数和体积分数梯度的变化Fig.8 Changes of the arrival time of the maximum pressure rise rate with volume fraction and volume fraction gradient under different working conditions

1.4 体积分数梯度对连通装置内最高温度的影响

对不同工况条件下最高温度、最高温度所处的位置、达到最高温度时刻进行了分析，见表6 和表7，表6 为连通装置不同体积分数时最高温度情况，表7 为连通装置不同体积分数梯度时最高温度情况。通过分析表6 和表7 可知，连通装置内均一体积分数为6.517%～8.067%，且大容器区域1 中心点火时，最高温度位于区域1；连通装置区域1 体积分数6.0%体积分数梯度为2.0%～8.0%，且区域1 中心点火时，最高温度位于区域5。

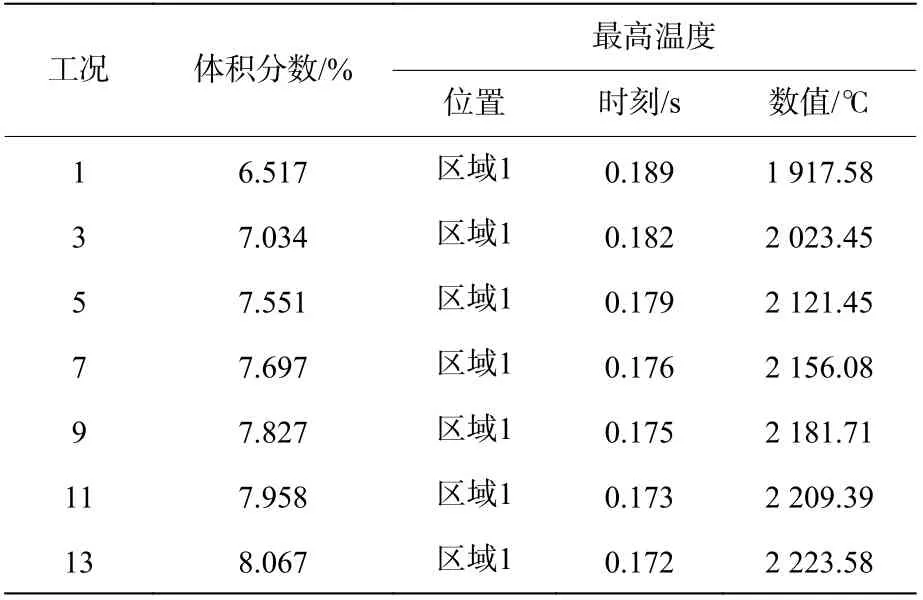
表6 连通装置不同均一体积分数下最高温度相关参数Table 6 Related parameters of the maximum temperatures in connected devices with different volume fractions

表7 连通装置不同体积分数梯度时最高温度相关参数Table 7 Rrelated parameters of the maximum temperatures in connected devices with different volume fraction gradients

图9 所示为不同工况条件下最高温度随体积分数/体积分数梯度变化曲线图。通过图9 可知，连通装置最高温度随均一体积分数值增大而升高，约成线性关系；连通装置最高温度随体积分数梯度的变化不是线性关系，最高温度与体积分数梯度的变化曲线出现先升高后降低的趋势，体积分数梯度为4.0%时，达到最高温度。这是因为当均一体积分数值越接近当量比体积分数时，爆炸越激烈，因此最高温度也越高。研究中不同体积分数梯度工况下比对应的均一体积分数工况的最高温度偏高，说明连通装置内相同总量的CH4，区域1 体积分数低，区域2 至5 体积分数依次增高，区域1 中心点火时，具有体积分数梯度的工况比对应的均一体积分数工况释放的能量多。图10 所示为不同工况条件下最高温度时刻值随体积分数/体积分数梯度的变化。由图10 可知，最高温度时刻随体积分数的增大而提前，并约成线性关系；而最高温度时刻随体积分数梯度的增大先提前再滞后。这是因为，在6.517%～8.067%范围内，随着体积分数的增大，越来越接近CH4的化学当量体积分数，越接近化学当量体积分数，爆炸反应越剧烈，释放的能量越大，因此，达到最高温度的时刻越提前。

图9 不同工况下最高温度随体积分数和体积分数梯度的变化Fig.9 Changes of the maximum temperature with volume fraction and volume fraction gradient under different working conditions

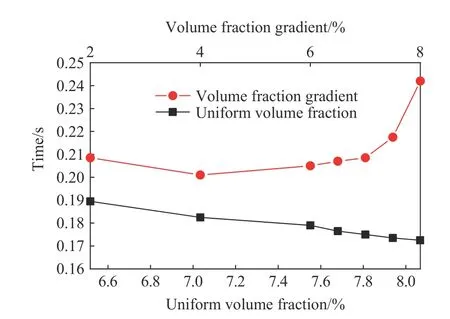
图10 不同工况下最高温度时刻值随体积分数和体积分数梯度的变化Fig.10 Changes of the arrival time of the maximum temperature with volume fraction and volume fraction gradient under different working conditions

1.5 体积分数梯度对连通装置内最大速度的影响

对不同工况条件下最大速度、最大速度所处的位置、达到最大速度时刻进行了分析，见表8和表9，表8 为连通装置不同体积分数时最大速度情况，表9 为连通装置不同体积分数梯度时最大速度情况。通过分析表8 和表9 可知，连通装置内均一体积分数为6.517%～8.067% 及区域1 体积分数6.0%体积分数梯度为2.0%～8.0%，且区域1 中心点火时，最大速度位于区域4。这是因为当连通装置大容器发生爆炸时，细长管道内从大容器方向向小容器方向气流速度持续加大，呈不断加速过程，因此，与小容器相连的管道内速度最大，可达400～600 m/s。

连通装置最大速度随均一体积分数值增大而增大，约成线性关系；连通装置最大速度随体积分数梯度的变化不是线性关系，最大速度随体积分数梯度增大先增大后减小。这是因为，均一体积分数值越接近当量体积分数，爆炸反应越激烈，连通装置内最大速度越大。最大速度时刻值随体积分数的增大而降低，并约成线性关系；而最大速度时刻随体积分数梯度的增大先提前再滞后。这是因为，在6.517%～8.067%范围内，随着体积分数值的增大，越来越接近CH4的化学当量体积分数，越接近化学当量体积分数，爆炸反应越激烈，因此，达到最大速度的时刻越提前。

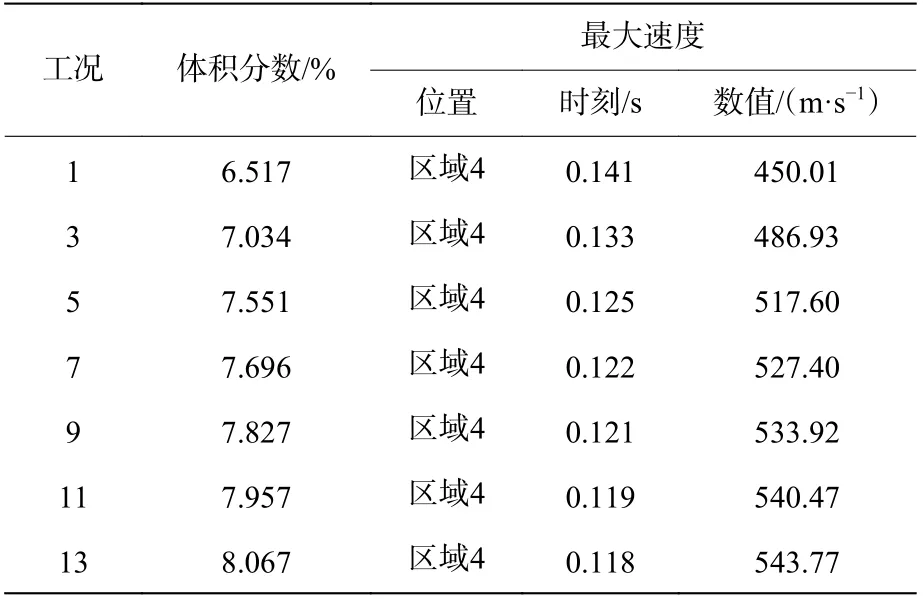
表8 连通装置不同体积分数时最大速度相关参数Table 8 Related parameters of the maximum velocities in connected devices with different volume fractions

表9 连通装置存在不同体积分数梯度时最大速度相关参数Table 9 Related parameters of the maximum velocities in connected devices with different volume fraction gradients

1.6 结果分析

在区域1 中点火爆炸后，未燃气体迅速膨胀，产生火焰锋面前后的密度差导致流体力学不稳定，膨胀比越大，流体动力学不稳定易使火焰失稳，热膨胀比可用如下公式计算[21]：

式中：σ 是热膨胀比，ρu是未燃气体密度，ρb是燃烧产物体积分数，ρu和 ρb可通过GASEQ 软件计算得到。

通过计算，区域1 中6.0%体积分数的甲烷燃烧热膨胀比为5.598，当区域1 气体完全燃烧，体积完全膨胀后为335.88 L，该数值远大于其他区域的体积总和，这意味着区域1 的未燃气体会将区域2～4 的气体全部压缩至区域5 中。

从整个爆炸过程来看，各区域内的气体混合物温度随容器中压力的升高而增加，因此可近似的看作绝热压缩的过程，绝热压缩使得未燃气体温度升高，对火焰燃烧速率产生了影响[22]，即：

式中：Su为火焰速度，Kr为室温下的燃烧速速率，Tu为未燃气温度，T0为初始温度， p0为初始压力，p 为爆炸压力，β是压力对燃速的影响因子。

文中涉及的7 种体积分数梯度工况，刚好经历贫燃至富燃的燃烧过程，而由贫燃向富燃转变过程中，最大爆炸压力、最大爆炸压力上升速率、火焰温度及最大速度总体均呈现先升后降的趋势。

区域1 内点火后发生层流燃烧，通过区域2、区域3、区域4 传播后，由于容器形状改变和管道刚性壁面的作用，火焰受到扰动，由层流燃烧转变为湍流燃烧，加速向区域5 传递，并对区域5 进行了预压缩，在压力累积与喷射火焰的共同作用下，区域5 直接发生了湍流燃烧，因此，压力高，上升速率快。

区域2～4 均为管道内，管内流团燃烧时，因体积膨胀而对周围介质作功，从而在火焰前方形成压缩波，诱导和加速当地质点的运动。火焰因此而变形，燃烧面积增大，燃烧速率加快，加速火焰的进一步推动又导致火焰阵面的更大变形。由于壁面附近存在粘性边界层，流速的增大会使管内出现湍流。大涡湍流使火焰皱褶，增加燃烧面积，小涡湍流可提高火焰内部的有效输运能力，这些都有助于提高燃烧速率。湍流强度随轴向流速的增加而增加。当湍流足够强时，未燃流团将被火焰所吞食形成燃烧的相干流块。这些流块在轴心附近温度高、流速大，壁面附近温度低流速小[23]。推测由于可燃气体在轴向体积分数呈不均匀分布，导致区域2～4 内湍流程度呈现较为复杂的变化，在总体先升后降的趋势下发生波动，根据式（7）可发现最大爆炸压力、最大爆炸压力上升速率、最大温度及最大速度均会受到一定影响。

2 结 论

（1）连通装置均一甲烷体积分数6.517%至8.067%，且大容器中心点火工况时，最大爆炸压力、最大爆炸压力上升速率、最高温度和最大速度，以及这些爆炸参数达到最大值时的时刻值随体积分数值的变化约呈线性关系；（2）连通装置大容器甲烷体积分数6.0%，体积分数梯度为2.0%～8.0%，且大容器中心点火时，最大爆炸压力、最大爆炸压力上升速率、最高温度和最大速度随体积分数梯度总体上先增大后减小，但由于管道内湍流程度高呈现较为复杂的变化，在体积分数梯度6.0%～7.5%之间可能出现波动；（3）连通装置内均一甲烷体积分数在6.517%～8.067%范围内，且大容器内甲烷的体积分数6.0%，体积分数梯度为2.0%～8.0%，大容器中心点火时，最大爆炸压力位于小容器内；（4）连通装置内均一甲烷体积分数在6.517%～8.067%范围内，且大容器内甲烷的体积分数为6.0%，体积分数梯度为2.0%～8.0%，大容器中心点火时，最大压力上升速率位于管道1 或管道2 中；（5）连通装置内均一甲烷体积分数为6.517%～8.067%范围内，大容器中心点火时，最大温度位置在大容器内；连通装置大容器内甲烷的体积分数为6.0%，体积分数梯度为2.0%～8.0%时，大容器中心点火时，最高温度位置在小容器内；（6）由于火焰传播在管道内呈现持续加速现象，因此连通装置内均一甲烷体积分数为6.517%～8.067%范围内，大容器中甲烷体积分数6.0%，体积分数梯度为2.0%～8.0%，且大容器中心点火时，最大速度位于管道3，速度值可达400～600 m/s。