爆炸冲击下珊瑚砂动态本构模型*

董 凯，任辉启,，阮文俊，黄 魁，步鹏飞

（1. 南京理工大学能源与动力工程学院，江苏 南京 210094；2. 中国人民解放军军事科学院国防工程研究院，河南 洛阳 471023）

随着我国海上丝绸之路重大战略的逐步实施，岛礁防护工程的建设需求被密切关注。珊瑚砂广泛分布于我国南海岛礁和瀉湖中，它作为覆土层、填充材料等应用于岛礁工程中。在岛礁工程面临突发的动力灾变时，珊瑚砂往往先受到来袭弹丸的侵彻、爆炸作用，而成为重要的研究对象[1-2]。

近些年，虽然对于珊瑚砂的本构关系开展了一些研究，但模型主要应用于沉桩、土工建设以及流变分析等低应变率的工程中[3-5]，而对中高应变率加载下珊瑚砂的研究，多见于力学特性分析、颗粒破碎和耗能的研究中，且阐述了颗粒破碎与压缩特性之间的联系[6-9]。这些研究成果对推动岛礁建设具有重要的作用，然而对于解决复杂的爆炸、侵彻等非线性问题，需要借助于大型商用计算软件如LS-DYNA、AUTODYN 等进行分析，如徐学勇[10]使用有效应力弹塑性本构模型对饱和钙质砂在爆炸下的动力响应做了分析。但目前对干燥珊瑚砂动态本构模型的研究十分匮乏，面对大量的实际工程计算需求，急需确定出可嵌入有限元程序中并适用于侵彻、爆炸计算的模型和参数。

砂土的力学参数随地域分布的不同呈现多样化，且模型在应用时往往局限于特定的条件，这使冲击下砂土本构关系具有多种表述形式。目前，广泛应用的模型大多采用以下两种框架构建：（1）基于冲击动力学实验（如SHPB 实验、泰勒杆实验、飞片冲击等）获得材料的高应变率压缩方程，结合描述偏应力的弹塑性关系构成流体弹塑性模型[11-12]；（2）使用静力学下的基本模型构架，通过增加率相关的参数考虑应变率效应，将模型适用于高应变率加载时的计算[13-14]。两种框架构建的本构模型在陆源砂土中均得到了广泛的应用，而在多孔易破碎的珊瑚砂中模型的适用性尚未确定，因此珊瑚砂动力学模型框架适用性的研究应作为模型研究的首要工作。

本文中，根据静态、动态力学实验结果，分别基于流体弹塑性模型和Perzyna 黏塑性帽盖模型确定珊瑚砂的模型参数，借助LS-DYNA 有限元程序实现模型在珊瑚砂中的应用，通过对弹丸侵彻珊瑚砂过程以及平面波加载下珊瑚砂中应力波衰减过程的数值计算验证模型的有效性，同时对不同压实密度下珊瑚砂的侵彻规律、爆炸应力波衰减规律进行计算，拟对武器战斗部在珊瑚砂中的侵彻、爆炸的研究提供重要参考。

1 本构模型和参数

1.1 基于剪切屈服和体积压缩规律的本构模型

珊瑚砂为脆性松散孔隙岩土材料，在冲击、爆炸等强动载下具有流体特性，并伴随着大量的颗粒破碎。高应变率（102s−1以上）下的体积压缩规律能准确地体现在冲击受压过程中材料的宏观压密现象，压实过程在物理上表现为体积不可逆压缩行为，与静水压有关，因此可用不可逆加、卸载路径下的压力-体应变函数即物态方程确定。剪切屈服特性采用正应力与偏应力之间的二次函数描述。由于物态方程是在高应变率下测得的，可适用于爆炸冲击计算，模型中不包含直接体现应变率的参数。LS-DYNA 中的5#材料模型（*MAT_SOIL_AND_FOAM）能很好表达该类模型[15]，其本质属于流体弹塑性模型，在爆炸、侵彻计算中得到广泛引用[16-18]，然而模型参数的确定方法未见明确报道，针对珊瑚砂的参数也少有研究。

1.1.1 屈服面函数

假设剪切强度准则可由3 个参数a0、a1、a2构成的二次函数F（J2, p）表达，屈服函数上的偏应力第二不变量J2与平均静水压力p 的关系定义为：

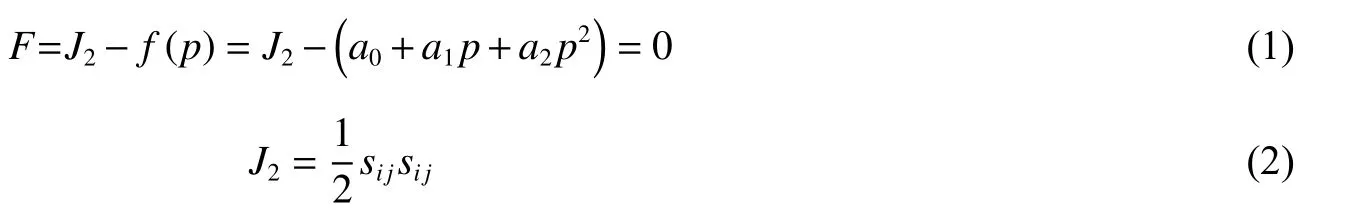
土力学中，通常认为无黏性砂的黏聚力为零。而大量实验结果表明，珊瑚砂存在一定的黏聚力[19-20]，主要源于不规则棱角的砂颗粒间的相互咬合，剪切时需要破坏此咬合结构才能达到破坏。Fasanella 等[17]给出a0=a1=0 来表征黏聚力为零，这与实际是不相符的。Wright[21]给出了确定屈服面参数的方法，但公式中存在一些错误，这里修正如下。

在剪切屈服面上，珊瑚砂符合Mohr-Coulomb准则，强度包络线如图1 所示。在破坏面上有关系式：

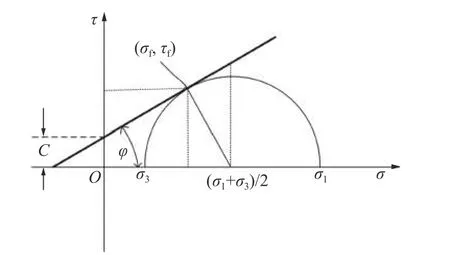
图1 确定屈服参数的摩尔圆Fig.1 Mohr’s circle geometry used to determine yield surface parameters

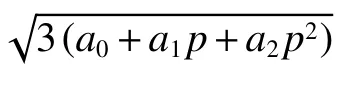
式中：σx为测得的轴向应力，在试样均匀化加载的条件下与正应力相等，在屈服时 σf=σx；σr为侧限压力；ξ为侧压力系数，定义为ξ =σr/σx，并通过SHPB 实验确定ξ =0.495。为便于公式推导，这里近似取p=2σf/3，可依据式(4)得到：

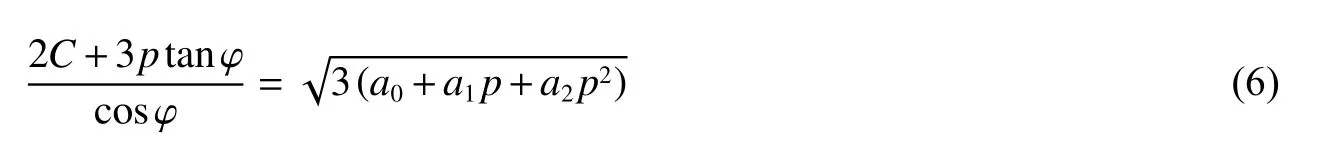
并可得到：

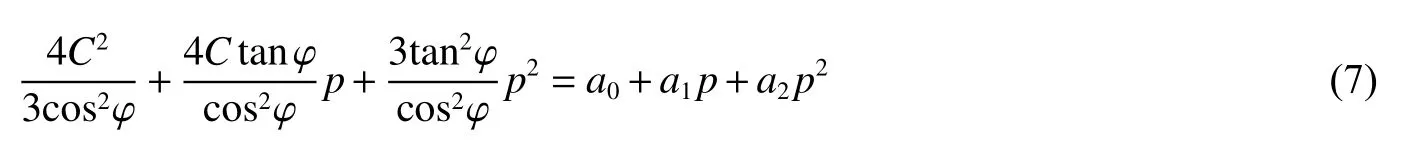
则屈服面参数可表示为：

文献[16]中的土壤模型参数被广泛应用于数值计算中，根据其中参数a0=3 400 kPa2，a2=0.30，利用上述方法计算得到拟合参数a1=63.96 kPa，与文献[16]中a1=70.33 kPa 进行对比，误差约为9.06%。可见，该方法可对屈服面参数进行确定。

根据直剪实验结果，珊瑚砂的黏聚力C=7.24 kPa，内摩擦因数tan φ=0.462，由式(8)可得到：a0=84.77 kPa2，a1=16.23 kPa，a2=0.777。由于岩土材料对温度的敏感性较低，模型没有考虑温度项的影响。当静水拉应力超过了拉伸截断阈值时，则设置拉应力为截断阈值且偏应力张力为零。由于松散的珊瑚砂无法承受拉伸状态，可取拉伸截断阈值为零。

1.1.2 冲击时平均压力-体应变方程

在高荷载作用下，多孔珊瑚砂被压缩密实，引起体积模量的增大，也称为材料的压硬性。由于珊瑚砂的颗粒破碎特性，加载初期卸载后基本不发生回弹，但在压实后材料凝聚为块状，卸载时可认为弹性卸载。因此，使用分段物态方程分别描述加、卸载行为：

式中：p 为平均压力，ɛV为体积应变。

高应变率压缩曲线对于模型的确定至关重要，然而通过SHPB 实验获得的曲线应变仅达到约0.12，对应的应力也往往不超过20 MPa，无法描述高孔隙率的珊瑚砂动态压实特性。通过比较静态与动态的应力应变曲线特征，可发现：（1）动态屈服应变与静态近似相等；（2）珊瑚砂没有明显的应变强化拐点εh，表明在压实过程中颗粒破碎比较平稳，变形机制未发生根本变化；（3）珊瑚砂在屈服后强化因数σd/σs随应变的增加表现出线性关系[23]。

基于上述结论，假设线性关系持续至压实状态，根据文献[23] 中相对密实度Dr为0.90（密度为1.260 g/cm3）的静态、高应变率下的一维压缩应力应变曲线，以准静态应力应变为基准，考虑强化因数的影响（σd/σs=1.663），结合测得的围压将准静态一维应力应变曲线换算成高应变率压力-体应变曲线，如图2所示。文祝等[22]通过预压方法确定了珊瑚砂的压缩方程，为p-ɛV关系的拟合提供了有效的方法，与本文确定的压缩曲线相比，整体趋势保持一致，但由于级配的不同导致曲线存在一定差别。两种方法中最大应力均达到100 MPa 以上，使用应变率强化因数拟合压实段物态方程的方法，有如下优点：（1）能够准确描述动态下初始阶段的屈服特性；（2）避免了预压阶段未计及的应变率效应问题。

根据实验结果[23]确定了3 种不同密度的珊瑚砂的p-ɛV曲线，如图3 所示。随着密度的增大，在相同体应变下受到的压力更大，为了准确描述屈服和硬化特性，宜采用分段函数表达，拟合的物态方程为：

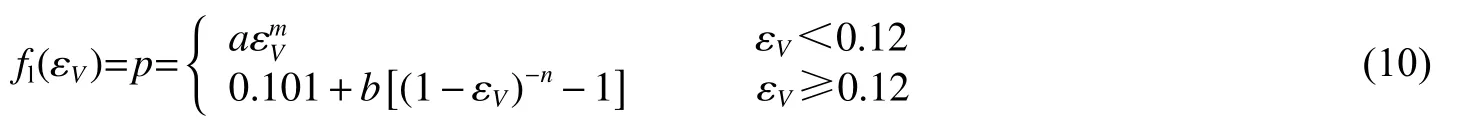
式中：a、m、b、n 均为密实度Dr的线性函数，模型的适用性因参数的线性特征而增强。它们可分别表示为：

此外，模型中加载体积模量K 可由SHPB 实验确定，取弹性条件下的初始值，砂土材料泊松比µ通常为0.3，可确定剪切模量G=3K(1-µ)/[2(1+µ)]，卸载体积模量Ku可根据压实段的模量确定[21]。综合以上，得到基于5#模型的3 种密度珊瑚砂参数，见表1～3。

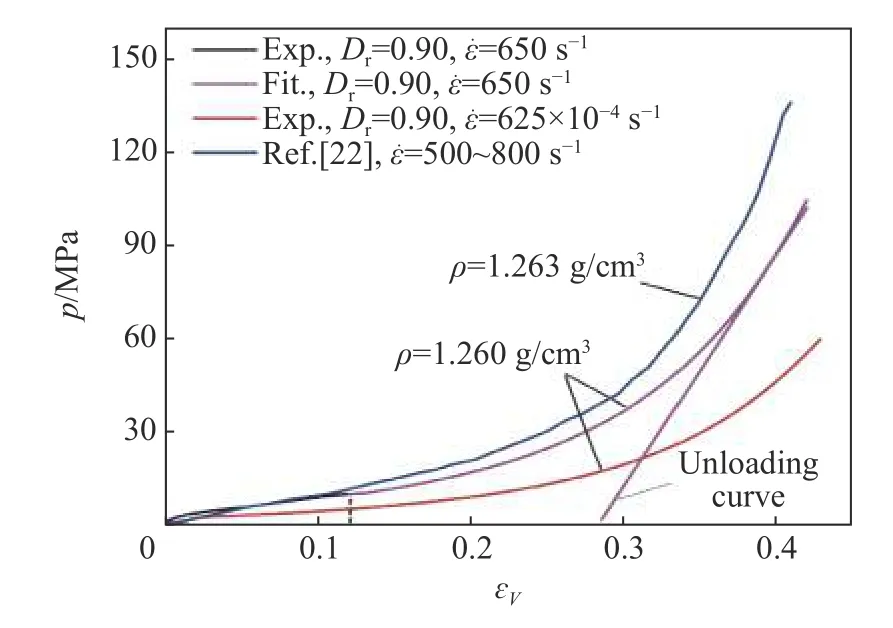
图2 平均压力-体应变的拟合曲线Fig.2 Average pressure-volumetric strain fitting curves

图3 在不同相对密实度下平均压力与体应变的关系Fig.3 Average pressure-volumetric strain curves under different compactness levels

表1 当 D r=0.30时珊瑚砂的5#材料模型参数Table 1 Parameters of 5# constitutive model for coral sand when Dr=0.30

表2 当 D r=0.60时珊瑚砂的5#材料模型参数Table 2 Parameters of 5# constitutive model for coral sand when Dr=0.60

表3 当 D r=0.90时珊瑚砂的5#材料模型参数Table 3 Parameters of 5# constitutive model for coral sand when Dr=0.90

1.2 基于Perzyna 形式的黏塑性帽盖模型

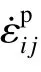
定义帽盖模型的屈服函数f 为应力张量第一不变量I1和偏应力第二不变量J2的关系，屈服面可分为3 部分（见图4），以下简单介绍。

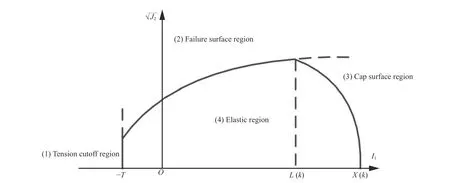
图4 黏塑性帽盖模型的屈服面Fig.4 Yield surface for viscoplastic cap model

（1）当 I1≤−T时，定义为拉伸失效面部分，可表示为：

式中：−T 为材料拉伸截止阈值。

（2）当 − T＜I1＜L(k)时，定义为强度失效面区，表示为：

破裂面为非硬化的，因此采用不考虑硬化的改进Drucker-Prager 形式，为：

式中：α、β、γ、θ 为材料特性相关的参数。

（3）当 I1≥L(k)时，定义为帽盖面部分，表示为：

观察患者呼吸机相关性肺炎的发生率,若通气治疗48h后符合:①X线胸片示新的或进行性肺浸润;②发热;③外周血白细胞计数>20.0×109/L或C反应蛋白>8mg/L;④气道分泌物细菌培养阳性。基础条件为X线胸片所示改变,若另外3条中2条符合,即可诊断患者患有呼吸机相关性肺炎[4]。

帽盖面定义为半椭圆形，为：

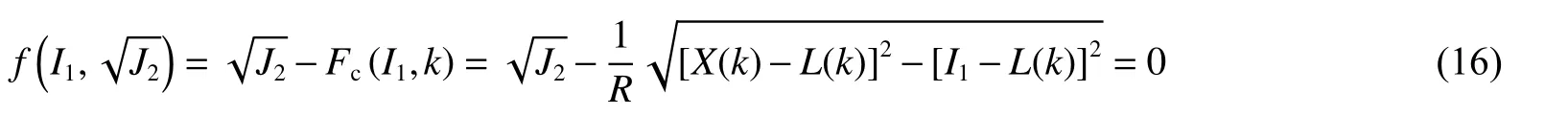
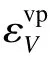
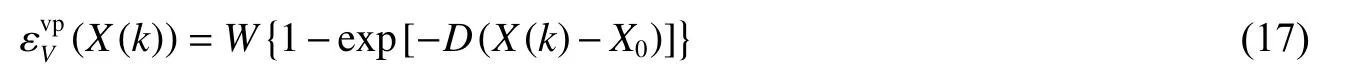
式中：X(k)位于帽盖面与横轴I1轴的交点，为：

L(k)为帽盖在开始位置时的静水压值，并符合：

由此，帽盖面可以表示为：

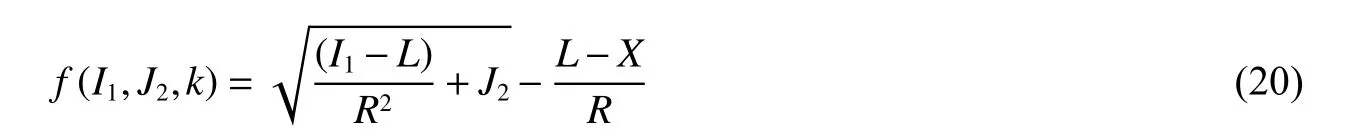
式中：W 为最大塑性体应变参数，D 为体积变化率参数，X0与帽盖面在横轴的初始位置有关。

Perzyna 黏塑性帽盖模型需确定14 个参数：W、D、R、X0为帽盖面函数的参数，α、β、γ、θ 为强度失效面函数中的参数，T 为拉伸截止面中的参数，η、f0、N 为描述黏塑性流动法则的参数，还有，描述珊瑚砂的弹性响应阶段的加载体积模量K 和剪切模量G。

丁育青[14]给出了该模型参数的详细确定方法，并应用于非饱和黏土中的爆炸计算，结合珊瑚砂的三轴围压实验[20]、准静态压缩实验和SHPB 实验结果[23]拟合得到了密实度0.30 珊瑚砂的Perzyna 模型参数，见表4。由于Perzyna 黏塑性模型参数较多，需依靠大量的力学实验确定，这里基于力学实验结果仅拟合得到了一组参数用于分析计算，模型需使用LS-DYNA 中的二次开发模块自定义本构，具体算法可参考文献[13-14, 24]。

表4 当 D r=0.30时珊瑚砂Perzyna 黏塑性帽盖模型参数Table 4 Perzyna viscoplastic cap model parameters of coral sand when Dr=0.30

2 数值模拟结果和分析

2.1 算例和结果

苗伟伟等[25]针对珊瑚砂在弹丸侵彻下的规律进行了一系列的实验研究，获得了初速为351～972 m/s的弹丸侵彻深度，同时使用理论方法进行了侵彻深度的计算并获得了理想的结果。目前，对于砂土的侵彻模型大都基于空腔膨胀理论进行研究[26]，为了确定所建立模型的适用性，使用LS-DYNA 对实验的侵彻过程进行数值计算。实验中弹丸形状和尺寸如图5 所示，弹丸材料为35CrMnSiA 合金钢，质量为80 g，在侵彻计算时采用刚体模型（*MAT_RIGID），密度ρ=7.85 g/cm3，弹性模量E=210 GPa，泊松比µ=0.29。珊瑚砂采用5#模型（Dr=0.90，ρ=1.260 g/cm3）。模型中的密度参数与侵彻实验一致，弹丸与珊瑚砂采用侵蚀接触，采用1/2 对称三维模型，计算靶体为厚10 cm、宽30 cm、长160 cm 的立方体，网格划分如图6 所示，其中弹丸网格数量为4 194，靶体网格数量为600 万。

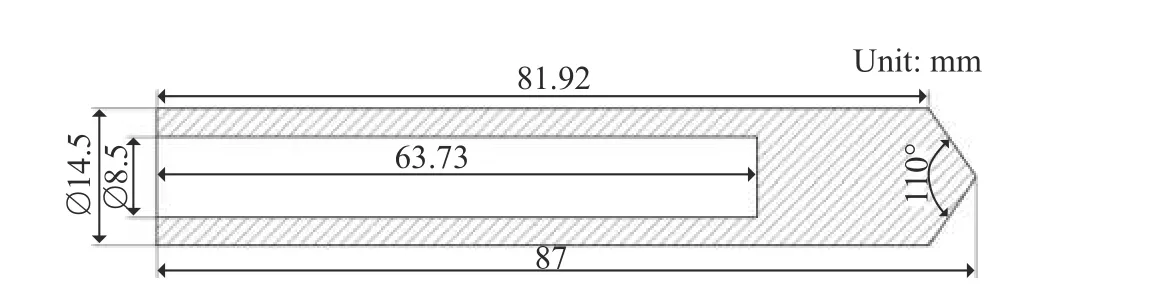
图5 弹丸形状和尺寸[25]Fig.5 Projectile geometry[25]

图6 侵彻计算模型网格划分（靶体为部分显示）Fig.6 Finite element mesh of calculated model (target is partially displayed)

计算得到的弹丸在不同入射速度下的最终侵彻深度如图7 所示，可见基于5#模型的计算结果与实验结果良好吻合，表明模型适用于刚性弹丸侵彻珊瑚砂的数值模拟。最终侵彻深度随入射速度的变化呈非线性关系，在不同初速侵彻时，弹丸速度随深度的下降规律如图8 所示。在侵彻初期由于过载非常大，随着入射速度的增大，弹丸速度下降非常明显，呈指数形式降低；随着速度的降低，过载明显减小。该结论与Omidvar 等[27]通过实验测得的土中弹丸侵彻过载的变化规律一致，表明砂土在刚性弹丸高速侵彻时呈流体响应。

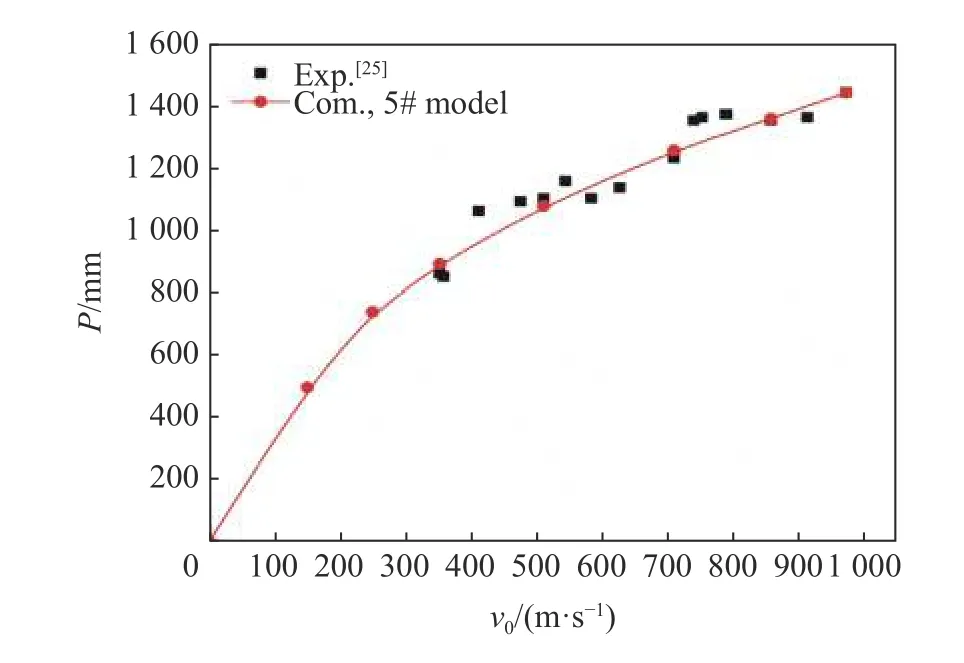
图7 最终侵彻深度与入射速度的关系Fig.7 Final penetration depth versus initial velocity

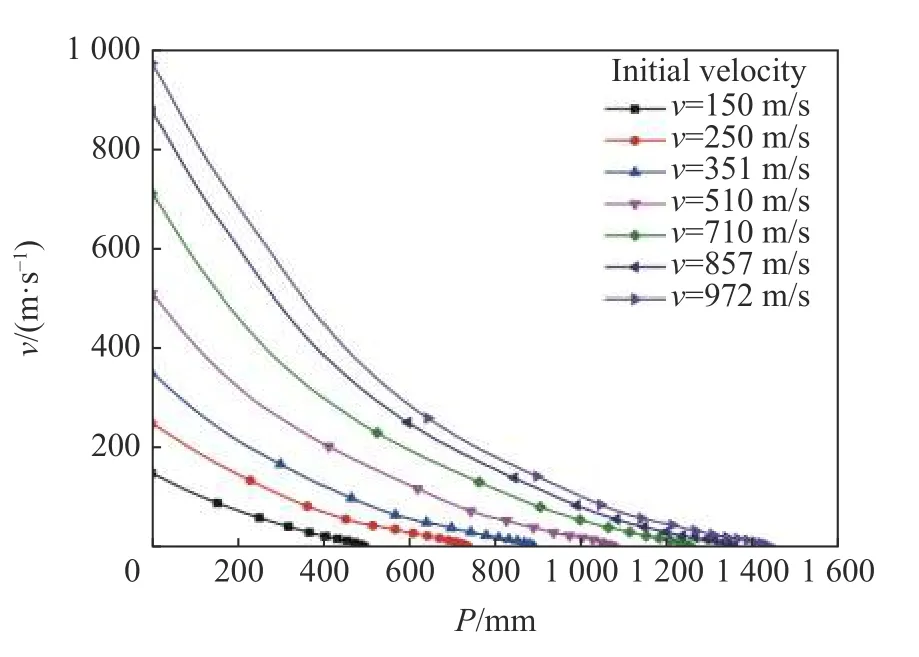
图8 不同入射速度时速度与深度的关系Fig.8 Velocity versus penetration depth at different initial velocities

在文献[25]的实验工况C27 中，弹丸以入射速度972 m/s 侵彻珊瑚砂，在侵彻初期弹丸速度远高于珊瑚砂波速（通常低于300 m/s）。用5#模型计算得到的珊瑚砂高压区呈锥形分布，具有典型的流体特征，如图9 所示。随着速度的下降，高压损伤区的边界轮廓逐渐由锥形向圆形过渡演化，侵彻过程中弹丸头部始终处于高压力作用状态，因此在头部出现了明显的磨蚀损伤，这与文献[25]的实验相符。在侵彻计算过程中，弹体发生偏转现象，文献[25]中虽未对该现象进行阐述，但弹道偏转情况在侵彻过程中难以避免，尤其在颗粒材料的侵彻中更加普遍[28]。通过以上结论与计算结果表明，基于5#模型对于弹丸侵彻珊瑚砂的数值计算是有效的。

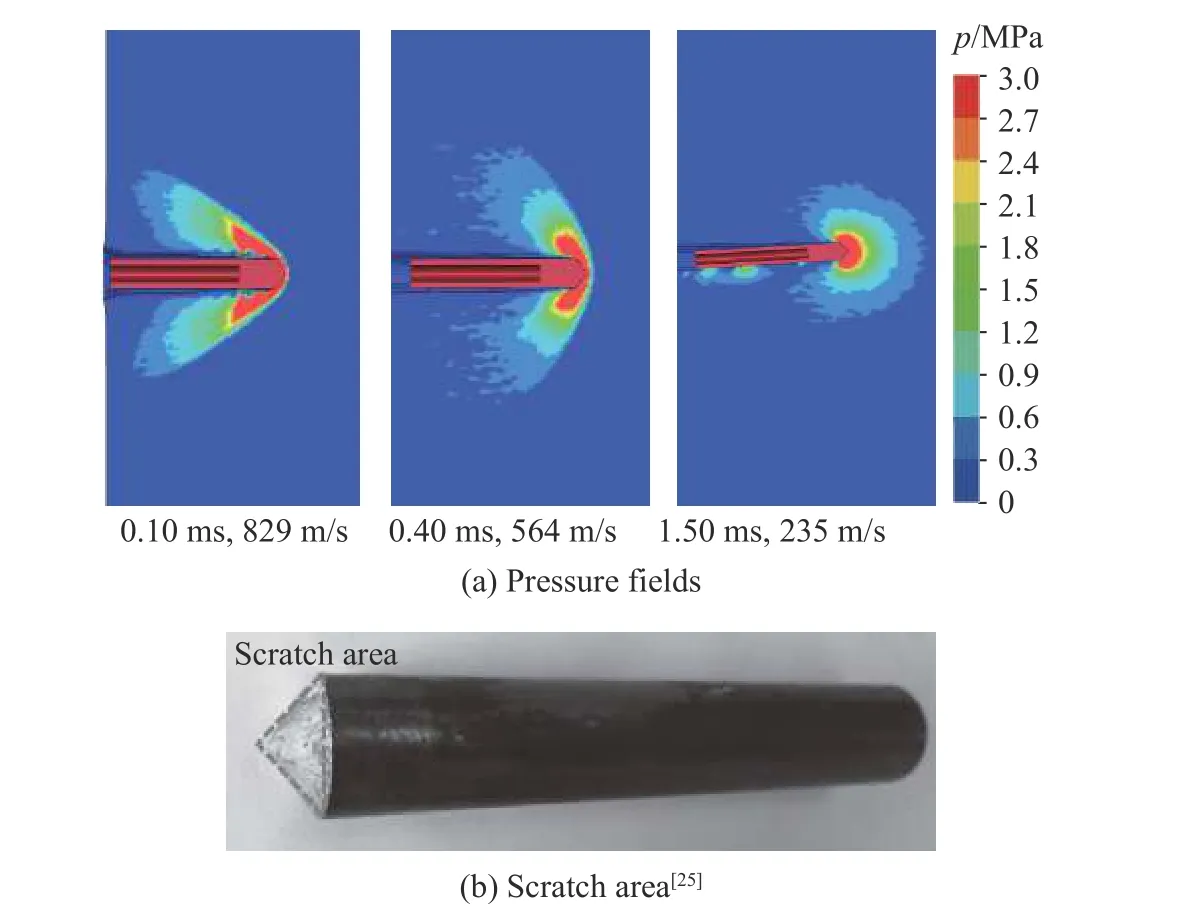
图9 珊瑚砂在不同时刻的压力场和弹丸产生的磨蚀区Fig.9 Pressure fields of coral sand at diffident times and scratch area of projectile

为了探索不同压实密度对珊瑚砂抗侵彻规律的影响，使用了1.1 节中的模型计算了弹丸对不同密实度珊瑚砂的侵彻，选择弹丸速度510 m/s 的情形进行对比，获得的速度随深度的变化关系如图10 所示。对比密实度0.30 的珊瑚砂，密实度0.90 的密度提高了约6.96%，侵彻深度降低了约5.03%。结果表明，提高压实度虽然可以降低侵彻深度，但3 种压实密度下侵彻深度相差很少。另外，本文的珊瑚砂为不良级配，其最大、最小干密度间的差很小，因此对侵彻深度的影响也很小。

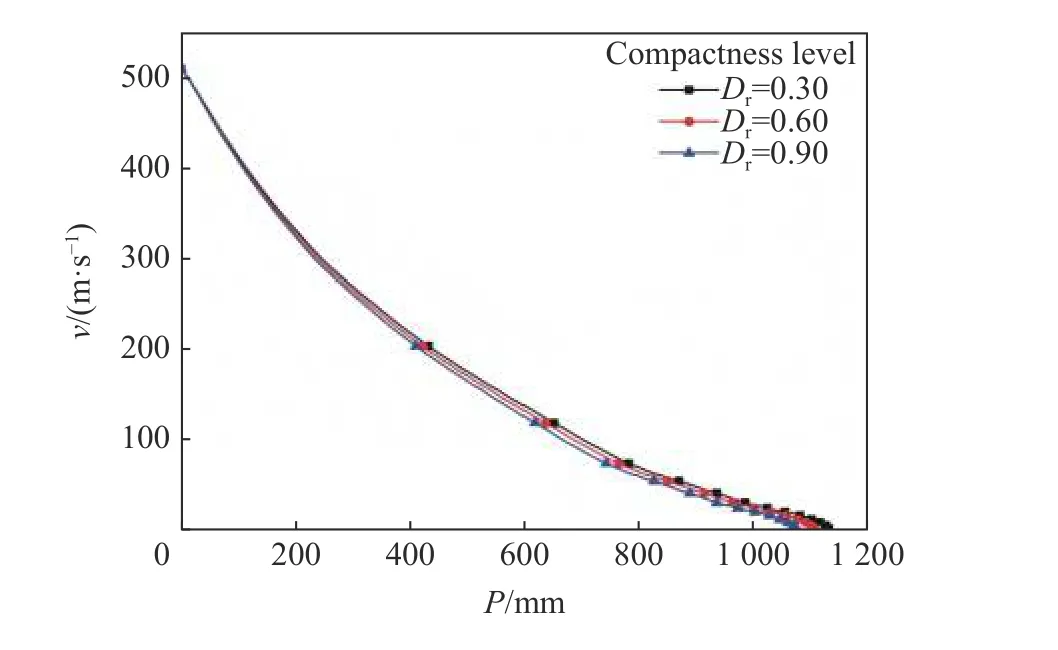
图10 不同压实密度时速度与深度的关系Fig.10 Velocity versus penetration depth under different compactness levels

2.2 珊瑚砂中爆炸应力波衰减规律

武器战斗部在砂土中爆炸时，产生的爆炸波沿砂土向周边传播，对地下结构造成破坏，这是防护工程中最关注的问题。砂土中应力波的衰减规律是决定传播至结构表面处压力的重要因素，而目前对珊瑚砂中的地冲击效应研究较少。

赵章泳等[29]通过实验确定了平面波加载下的珊瑚砂中应力波衰减规律，使用第1 节中确定的模型参数对该爆炸过程进行了数值计算，得到的应力波峰值衰减曲线如图11 所示。可见，5#模型计算得到的衰减曲线与实验较好吻合，而Perzyna 模型则略显刚硬，表现为应力波衰减缓慢。

两种模型计算得到的球形装药触地爆时爆炸波衰减的一般规律，如图12 所示，其中监测点1 位于比例距离0.2 m/kg1/3处，监测点2 位于比例距离0.3 m/kg1/3处。可以看出，两种模型在相同时刻达到监测点，表明计算得到的应力波速度一致。5#模型计算得到的应力波在衰减过程中表现出上升沿渐缓、长历时、低幅值的现象，于潇等[30]、Yu 等[31]通过SHPB 实验测量珊瑚砂中应力波衰减规律，也发现了该现象，认为颗粒破碎导致高频分量被过滤，Perzyna 黏塑性模型无法描述因颗粒破碎产生的波前观测弛豫现象，因此在易破碎的珊瑚砂中的计算存在较大误差。而5#模型的压缩曲线基于SHPB 实验测得，有关破碎引起的高压缩特性已经耦合于方程内部，能够表达珊瑚砂的宏观力学本质；同时，参考王礼立等[32]对塑性本构关系和流动型本构关系的研究可以推断，基于流动率确定的本构模型更符合干燥珊瑚砂在爆炸、侵彻下的变形规律。

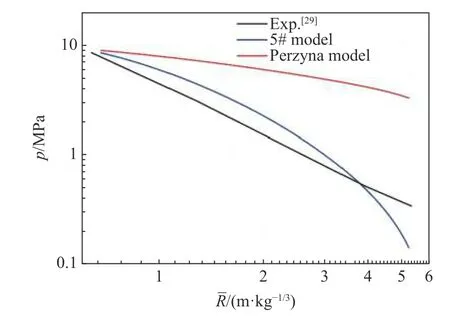
图11 峰值压力的衰减Fig.11 Calculated and experiment results of peak pressure attenuation

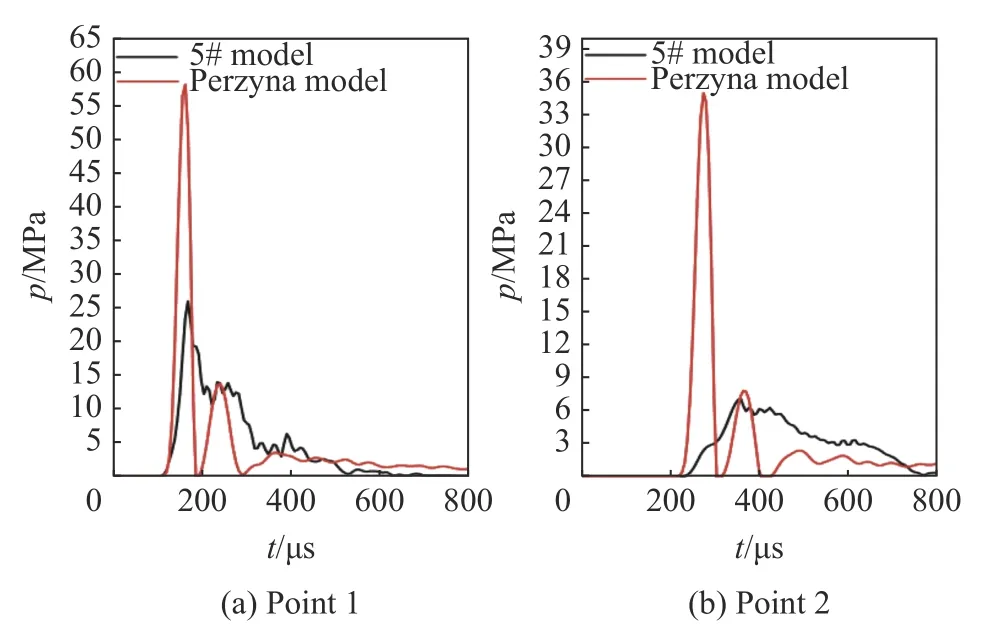
图12 两种模型压力波Fig.12 Pressure waves calculated by two models

珊瑚砂堆积密度对应力波衰减的影响同样具有举足轻重的作用，然而由于模型参数的局限，对压实密度这个参量影响爆炸波传播规律的研究较少。使用1.1 节中的5#模型参数，对3 种密度的珊瑚砂中的爆炸波衰减规律进行数值计算，采用触地爆炸模型（见图13）作为研究对象，炸药为200 g 的块状TNT，尺寸为10 cm×5 cm×2.5 cm，模型采用1/4 对称结构，在对称面施加对称边界，其余采用非反射边界条件，空气与珊瑚砂采用Euler 网格，均采用ALE 多物质单元，材料可在网格内流动，TNT 与空气的材料模型及相关算法可参考文献[33-34]。

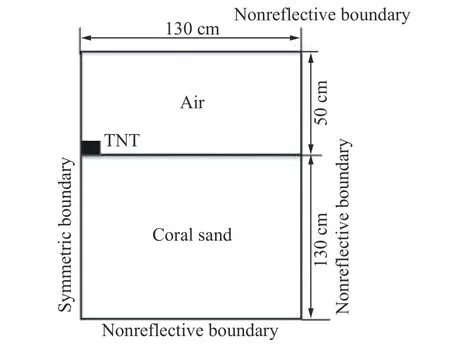
图13 计算模型Fig.13 Numerical model

块状炸药爆炸时产生近似球形波，介质表面爆炸时处于炸药正下方的压力最大，通过计算得到压力波峰值压力随比例距离的衰减关系如图14 所示。可见，松散的珊瑚砂具有更好的消波能力，相比密实度0.90，密实度0.30 的珊瑚砂应力峰值最高可降低26.1%。因此，工程应用中，在承载力允许的条件下，使用松散珊瑚砂更利于爆炸波的衰减。

图14 不同相对密度时爆炸峰值压力与比例距离的关系Fig.14 Peak pressure versus scaled distance under different compactness levels

综上所述，珊瑚砂的压实密度对于弹丸侵彻的应力波衰减存在一定的影响，为提高承载力和抗侵彻能力，往往需要提高压实密度；而面对爆炸波的冲击作用，又需要降低密实度以增强消波能力。因此，不论是评价武器对岛礁的毁伤效应还是岛礁防护工程的设计，珊瑚砂的动态本构模型研究都十分重要。

本文中研究的珊瑚砂为原状砂，在实验时保留了原生颗粒级配的完整性。工程中有时将砂土作夯实处理，密度超过原生砂的最大干密度但同时会引起颗粒破碎，此时，需对本构模型另做改进。

3 结 论

研究的两种珊瑚砂模型中：5#模型更适合于爆炸冲击下的数值计算；Perzyna 黏塑性帽盖模型中的参数需依靠较多的实验获得，在工程应用中略显不足，但其模型理论性较强，开发出考虑颗粒破碎的黏塑性帽盖模型将更符合珊瑚砂的变形规律。通过基本力学实验结果确定了珊瑚砂的本构参数，并通过数值计算获得了以下结论。

（1）对于应变率效应较敏感的珊瑚砂，使用动态增强系数确定压实段应力应变曲线的方法可以弥补SHPB 实验中无法将珊瑚砂加载至密实状态的不足，为拟合高应变率下的物态方程提供方法。

（2）在弹丸侵彻珊瑚砂的计算中，5#模型能表现出高应变率下的流动特征，对于珊瑚砂的应力场响应描述符合客观规律。

（3）流体弹塑性模型更能反映干燥珊瑚砂在爆炸作用下应力波衰减时出现的历时增长现象，Perzyna 黏塑性帽盖模型因对颗粒破碎描述的缺失，计算应力波衰减时得到的误差较大。

（4）不良级配的珊瑚砂由于最大、最小干密度相差较小，相对密实度对弹丸侵彻深度影响较小，但对于爆炸波的压力峰衰减影响较大。