岩石动态巴西圆盘实验中的过载现象*

夏开文，余裕超，王 帅，吴帮标，徐 颖，蔡英鹏

（1. 天津大学水利工程仿真与安全国家重点实验室，天津 300372；2. 天津大学建筑工程学院，天津 300350）

岩石材料在外部荷载作用下容易发生压缩、拉伸以及剪切破坏，岩石抗压强于抗拉的特性使得其在失效时的破坏模式主要表现为拉伸破坏。在深部岩石工程中，深部岩石在原位预拉伸应力和动态扰动（爆炸、地震波等）的共同作用下更容易发生失稳破坏，从而导致诸如“片帮”、“岩爆”等安全事故，严重危害地下构筑物的安全和稳定[1]。因此，准确获取岩石材料的拉伸强度对岩石工程的安全设计至关重要。

经过多年发展，学者们提出了多种岩石静态拉伸强度的测试方法，按照实验方式和原理不同可将它们分为直接拉伸方法和间接拉伸方法。直接拉伸方法[2]能够直接获取岩石的拉伸强度，但开展直接拉伸实验面临着两个问题，即实验操作精度要求高和实现单轴拉伸应力状态困难，实验操作不规范也容易导致试样的局部应力集中，从而出现不标准的破坏模式[3]。因此，近年来人们发展了许多间接拉伸测试方法，如巴西圆盘实验[4]、圆环实验[5]、三点和四点弯曲实验[6]以及Luong 实验[7]等。这些实验方法中巴西圆盘实验的应用最广泛，该方法于1978 年被推荐为国际岩石力学与工程学会（ISRM）岩石静态拉伸强度的标准测试方法。

静态条件下巴西圆盘实验拉伸强度 σT的计算公式为[8]：

式中：B 和D 分别为试样的厚度和直径，Pf为圆盘破坏荷载。

分离式霍普金森压杆（SHPB）是目前测试岩石等脆性材料动态力学响应的主流装置。Ross 等[9]最早借助SHPB 开展巴西圆盘实验并研究了混凝土材料的动态拉伸特征，这是SHPB 在岩石动态拉伸强度测试应用中的开端。在此之后，人们又利用SHPB 对各类岩石开展了大量的动态巴西劈裂拉伸实验[10-12]，总结了岩石材料劈裂拉伸强度的率相关性。

在试样满足动态力平衡的条件下，动态巴西圆盘实验中拉伸强度可按照式（1）确定，其中Pf为圆盘承受的动态峰值荷载。然而有学者通过观察测试结果，发现岩石的动态巴西圆盘拉伸强度往往高于动态直接拉伸强度，因此他们对动态巴西圆盘方法确定的拉伸强度值作为材料动态拉伸强度的有效性提出了质疑。Zhang 等[3]统计了不同加载率、不同种类岩石材料巴西圆盘实验和直接拉伸实验得到的拉伸强度的动态增强因子（DIF），发现相同加载率下巴西圆盘实验得到的DIF 较直接拉伸实验更高。Xia等[11]总结了通过不同的拉伸强度测试方法（动态直接拉伸、动态巴西劈裂以及动态半圆盘弯曲）测得Laurentian 花岗岩的动态拉伸强度，也发现相同加载率下动态劈裂拉伸强度比动态直接拉伸强度高，他们认为这种现象是由过载效应以及内摩擦效应引起的。关于这点，Mellor 等[13]在1971 年便观察到了静态巴西圆盘实验的过载现象，他们在实验过程中通过加载控制首先得到了主裂纹未贯穿圆盘的试样，而后继续对该试样进行加载，测试结果表明虽然圆盘试样中心点处已经发生了拉伸破坏，但试样的承载能力仍继续增加。

上述研究表明，在动态巴西圆盘测试中过载效应是真实存在的，为了探究岩石材料动态巴西圆盘实验中动态强度的过载现象及率相关性，本文中结合室内SHPB 装置对房山花岗岩动态劈裂拉伸强度的过载特性进行定量分析，同时结合颗粒流程序，模拟岩石材料动态巴西劈裂实验中的过载现象，揭示动态巴西圆盘实验过载效应产生的微观机理。

1 岩石动态巴西圆盘实验

1.1 分离式霍普金森压杆试验系统

借助分离式霍普金森压杆试验系统（SHPB）开展动态巴西圆盘实验，SHPB 通常由试验杆件（撞击杆、入射杆和透射杆）、试样以及信号采集系统组成（见图1）。SHPB 是利用应力波在试验杆件以及待测样品中的传播进行动力加载测试的实验装置。通过预先设置在入射杆、透射杆上的应变片可记录应力时程信息，根据一维应力波理论最终可计算得到试样的应力应变关系。

图1 ∅ 50 mm 分离式霍普金森压杆试验系统Fig.1 ∅ 50 mm split Hopkinson pressure bar system

撞击杆在气枪的作用下以一定的速度撞击入射杆，在入射杆杆端形成向右传播的压缩脉冲（入射波），由于试样与杆件的波阻抗不同，入射波会在试样处发生反射和透射。进入试样的应力波在其内部反复传播，最终导致试样的破坏。试样上的应力信号一般无法准确地直接测量，需要根据应力波理论计算杆件上测得的应变，以获得试样上的应力时程曲线。

应力波在物体中的传播存在横向弥散效应和惯性效应。横向弥散效应的存在限制了SHPB 杆件杆径的大小。利用SHPB 对岩石材料进行动态测试时，若利用原始的方波对试样进行加载很难满足动态力平衡条件。对此，有学者提出采用波形整形器[14]或者改变撞击杆的几何形状[15]来解决这个问题，本文中实验将采用黄铜材质的整形器进行波形整形。

1.2 试样动态力平衡及中心起裂时刻测量

通过对加载波形进行整形可以保证试样两端满足动态力平衡条件[16]，设入射杆、透射杆与样品的接触面分别为S1和S2，根据一维应力波理论，可以得到端面S1、S2上的力P1、P2分别为：

式中：E 为杆的弹性模量，A 为杆的横截面积，εi、εr和 εt分别对应入射波、反射波和透射波的应变信号。当且仅当试样两端的动态力平衡以后（见图2），即只有满足P1=P2的SHPB 实验才是有效的，才能够使用准静态的方法（式（1））对应变片采集到的数据进行简化和处理。

本文中所用的测试材料为房山细粒花岗岩，为了捕捉圆盘试样动态劈裂过程中的中心起裂时刻，在偏离试样中心位置d（d=5 mm）位置粘贴了1 枚应变片（见图3），根据Jiang 等[17]和Xia 等[11]的研究，圆盘中心破裂引发的周围区域应力的释放，具体表现为试样上应变片信号会出现一个显著的拐点，该拐点对应的时刻即为圆盘起裂时刻，假设t0时刻为圆盘中心点起裂时刻，已知岩石中波速cr=4 500 m/s，杆件中波速cb=5 270 m/s，圆盘直径为D，透射应变片与透射杆左端的距离L，那么试样上应变片采集信号的拐点时刻 T1为：

根据透射杆上波传播的距离对透射信号进行平移，得到圆盘中心起裂的对应时刻 T2为：

根据式（4）～（5），以试样上应变片起跳信号为原点，将透射波信号在时间轴上向左平移 | T2−T1|，并将其转化为试样两端应力信号，即可得到归一时间轴的试样整体应力与起裂时程信号，可据此获取起裂时刻圆盘中心点处的拉伸应力。

图2 典型动态巴西圆盘实验动态应力平衡验证Fig.2 Verification of dynamic stress balance in typical Dynamic BD test

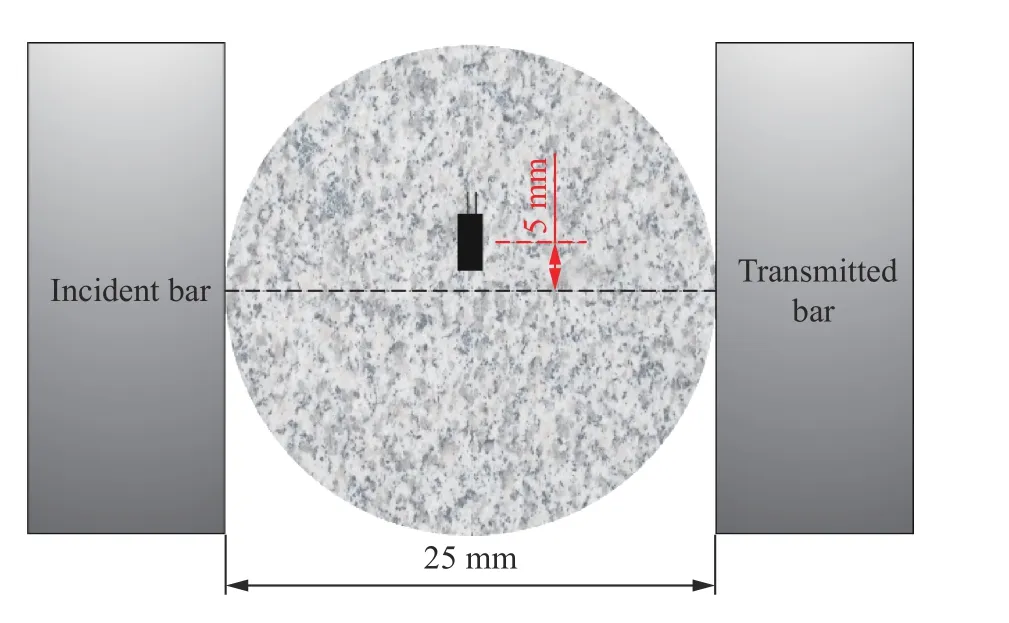
图3 试样起裂监测应变片粘贴位置Fig.3 Schematics of a strain gauge cemented on the specimen for detecting failure onset

1.3 过载修正及实验结果

为便于区分，定义试样应力时程曲线峰值为名义拉伸强度，过载修正后强度为真实拉伸强度。以180 GPa/s 加载工况为例，试样直径D=25.42 mm，透射应变片与透射杆左端的距离L=0.937 m，计算可知圆盘起裂对应的透射波所处时刻为T2=t0+180.62 µs，根据计算得到的时间差对该工况下透射应力进行修正（见图4），分析图像可以发现，试样名义拉伸强度为20.4 MPa，而圆盘起裂时刻应力19.49 MPa。而以同样的方法对418 GPa/s 加载率工况（见图5）进行分析，得到试样的名义拉伸强度和起裂时刻应力分别为25.30 MPa 和20.56 MPa。通过对比上述两幅图片可以明显地观察到：随着加载率的增加，圆盘起裂时刻应力与名义拉伸强度差异越大，过载现象越明显。为定量描述动态巴西圆盘实验中传统方法测量得到的拉伸强度的过载程度，定义动态巴西圆盘实验中的过载比 so为：

式中：σt为名义拉伸强度，σi为真实拉伸强度。

图4 180 GPa/s 加载率工况圆盘应力过载修正Fig.4 The overload correction for specimen’s tensile stress under 180 GPa/s loading rate

图5 418 GPa/s 加载率工况圆盘应力过载修正Fig.5 The overload correction for specimen’s tensile stress under 418 GPa/s loading rate

表1 为动态巴西圆盘实验得到的名义拉伸强度、真实拉伸强度、过载时间（名义与真实拉伸强度时间差）以及过载比的汇总，分析表1 中数据可以出，随着加载率的增加，圆盘动态拉伸强度的过载效应愈发明显：加载率从179.9 GPa/s 增加到1021.2 GPa/s，强度的过载比由0.045 增加到0.439。为了更直观地理解动态巴西圆盘实验中的过载现象，在图6 中绘制了名义拉伸强度与真实拉伸强度的关系，发现加载率越高名义拉伸强度与真实拉伸强度的偏差越大。房山花岗岩动态巴西圆盘实验中的过载比 so随加载率的增加呈近似对数型增长规律（见图7），其增长速度会随加载率的增大逐渐减小，过载比 so拟合曲线方程为：

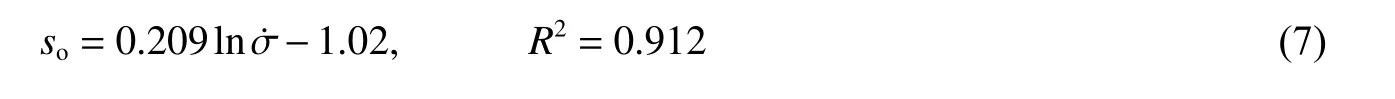
表1 动态巴西圆盘实验结果Table 1 Dynamic BD experimental results

图6 名义拉伸强度与真实拉伸强度Fig.6 Nominal tensile strength and the real tensile strength

图7 动态巴西圆盘实验过载比Fig.7 The overload ratio for dynamic BD tests

2 岩石动态巴西圆盘数值实验

2.1 SHPB 计算模型的建立与加载

采用PFC 建立的 ∅50 mm 的SHPB 实验系统数值模型，如图8 所示。为便于计算，入射杆与透射杆的长度分别为1.5 m 和1 m，采用线性接触模型（CBM）模拟，组成颗粒的粒径在0.75～1.25 mm 之间，圆盘试样直径为50 mm，采用线性平行黏结模型（PBM）模拟。在入射杆左端颗粒输入半正弦入射脉冲进行动态测试（输入脉冲脉宽和峰值与实验相同），图9 为本次模拟与实验所用入射波的对比情况。

图8 ∅ 50 mm 的SHPB 数值实验系统Fig.8 ∅ 50 mm split Hopkinson pressure bar numerical system

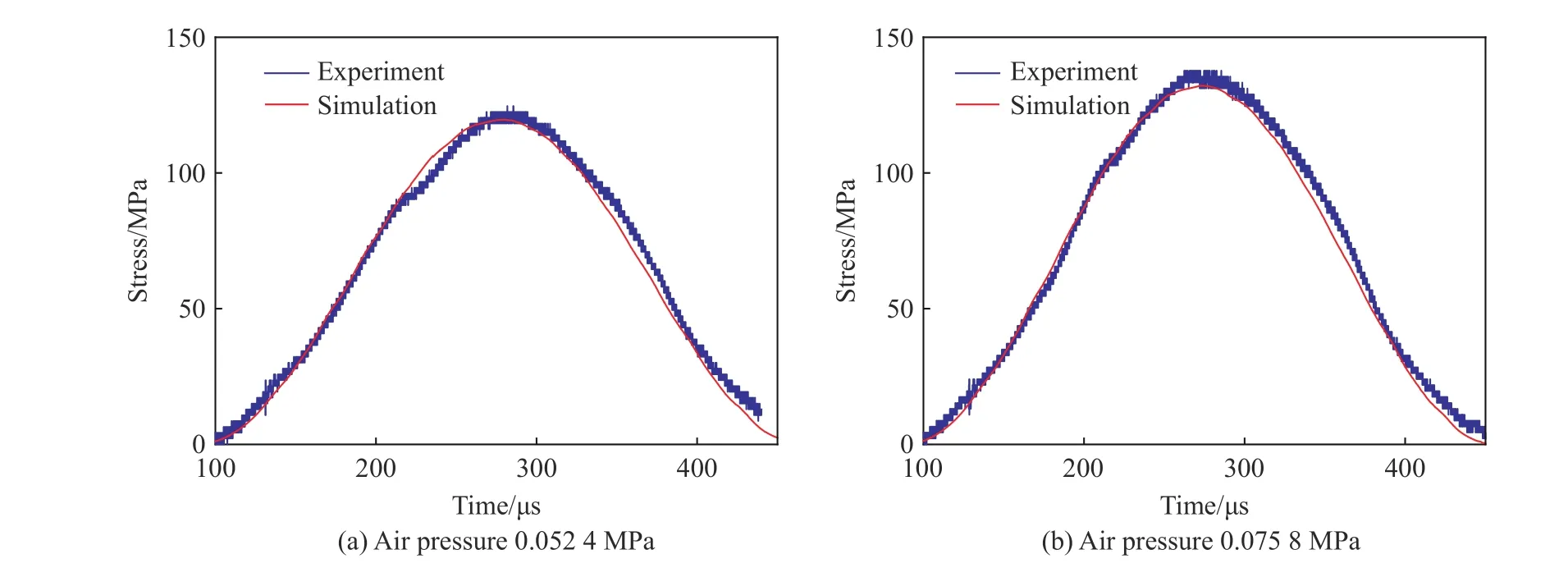
图9 实验与模拟入射波波形对照Fig.9 Incident wave comparison between lab experiment and numerical simulation

2.2 离散元模型宏、微观参数标定

在进行岩石材料离散元模型宏、微观参数标定时，主要参考Shi 等[18]的标定思路：

（2）法向-剪切刚度比 k∗控制弹性变形阶段的泊松比；

参数标定按照泊松比µ、弹性模量E、单轴压缩破坏模式及巴西圆盘名义拉伸强度的顺序依次进行，得到最终试样与杆件模型的主要微观参数，见表2～3；表4 为试样模型的宏观参数与通过静态实验所获得的宏观参数的对比，分析表4 中的数据可以看出，本文中使用的微观参数可以较好地模拟房山花岗岩圆盘的力学性能。

表2 试样主要模型微观参数Table 2 Parameters of the numerical specimen

表3 杆件主要模型微观参数Table 3 Parameters of the numerical bar

表4 模型宏观参数与材料宏观参数对比Table 4 Macroscopic parameters of the numerical model and real rock

2.3 线性平行黏结模型率效应修正

PFC 中平行黏结模型（PBM）不包含率相关的物理量，因此直接使用固定PBM 模型参数进行动态冲击实验模拟往往不能真实反映出材料强度的率相关性。为了解决这一问题，借鉴Yang 等[19]的经验，首先通过实验得到目标岩石拉伸强度与加载率的关系，再通过强度参数标定建立模型黏结强度与宏观拉伸强度的关系，从而得到模型黏结强度与加载率的关系，最后利用Fish 语言编程将真实材料强度的率效应引入计算模型中。

为探究PBM 模型的数值率效应，在图10 中绘制了实验和数值模拟获得的名义拉伸强度与加载率的关系。对实验名义拉伸强度 Ubts进行直线拟合，拟合方程为：

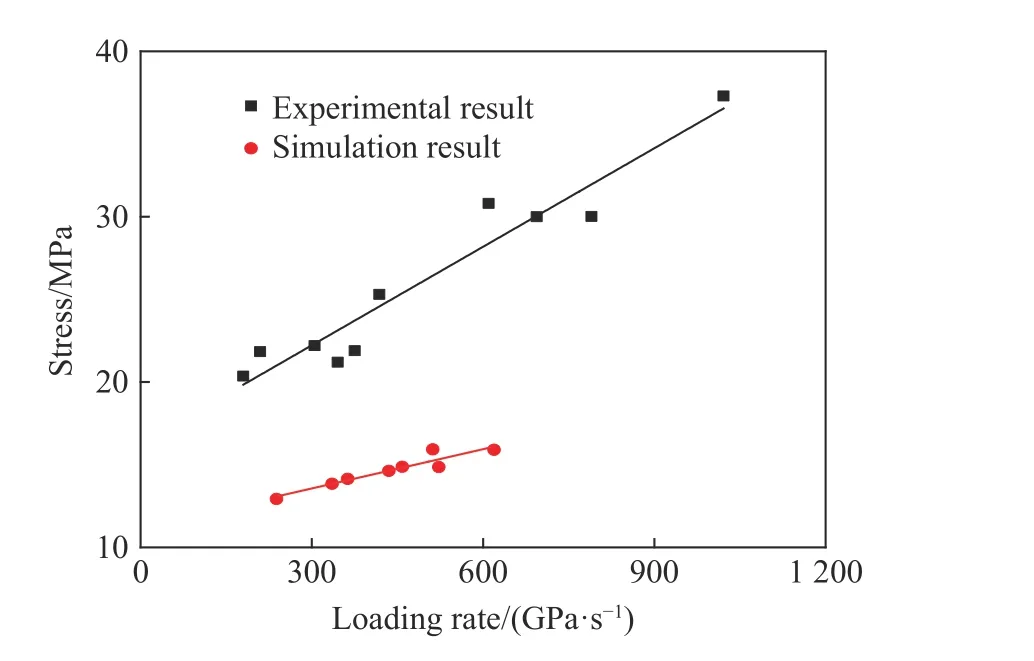
图10 实验与模拟名义拉伸强度的率效应Fig.10 The rate dependency for experimental and numerical nominal tensile stress

对比式（8）、式（9）可以发现，数值模拟得到的名义拉伸强度与加载率的拟合直线斜率明显小于实验数据拟合得到的斜率，说明模型参数固定时开展动态冲击实验模拟往往不能合理反应强度的率相关性。式（9）对应拟合直线斜率截距近似等于所设定内聚力值（23 MPa）的一半，据此我们得到考虑PBM模型参数的率效应描述方程：

由式（10）可以得到模型内聚力与动态名义拉伸强度以及加载率的关系式：

基于式（11），在任意加载工况下，只要知道实验加载率以及动态强度，即可推导出该实验工况下对应的黏结强度值。下面以气压为0.0524 MPa 的加载工况为例进行验证，输入的入射波波形如图9 所示，已知实验得到的试样加载率和强度分别为375 GPa/s 和21.9 MPa，计算得到模型黏结强度为38.325 MPa，代入该值进行数值模拟计算，采集到圆盘模型拉伸应力时程曲线如图11(a)所示，分析图像可以发现，此时模拟与实验圆盘拉伸应力在峰前段能够很好地重合，图11(b)为加载率为694 GPa/s 时实验与数值模拟得到的圆盘拉伸应力对比结果。

图11 不同加载率下实验与模拟圆盘的拉伸应力Fig.11 Experimental and numerical tensile stress under different loading rates

2.4 动态巴西圆盘数值实验中的过载效应

图12 为数值模拟得到的加载率为345.3 GPa/s 工况下试样两端的动态应力平衡结果。引入实验率效应修正后数值计算得到的名义拉伸强度的结果如图13 所示，分析图像可以发现，实验与数值模拟得到的名义拉伸强度数据之间无显著差异，表明率效应修正后PBM 模型参数可以很好地模拟真实岩石的动态力学行为。

图12 典型数值模拟动态应力平衡验证Fig.12 Verification of dynamic stress balance in typical numerical dynamic BD test

图13 实验与模拟名义拉伸强度Fig.13 Experimental and numerical nominal tensile strength

为进一步验证模型的准确性，对两种不同加载率（375、1 021 GPa/s）下的实验与数值模拟得到的试样破坏模式进行分析，对比结果如图14～15 所示。分析图像可以发现，数值模拟得到的试样破坏模式与实验基本相同：低加载率（375 GPa/s）下，圆盘试样的破坏模式为“中心开裂+两侧楔形破坏”；高加载率（1 021 GPa/s）下，试样的破坏模式为“中心开裂+径向条带状压碎”，这与Zhou 等[20]、Wu 等[12]研究中所述的破坏模式基本一致。

图14 375 GPa/s 加载率实验与模拟破坏模式Fig.14 Experimental and numerical disk failure pattern under 375 GPa/s loading rate

图15 1021 GPa/s 加载率实验与模拟破坏模式Fig.15 Experimental and numerical disk failure pattern under 1021 GPa/s loading rate

与实验类似，在圆盘表面设置应力监测圆，用相同的处理方法对数据进行过载修正，图16 为对应工况下模型拉伸强度的过载修正结果。图17 为动态巴西劈裂实验与数值模拟得到的拉伸强度过载比，从图中可以发现，模拟结果与实验结果基本呈现出类似的增长规律，这也在一定程度上验证了实验观测到拉伸强度过载效应的存在。

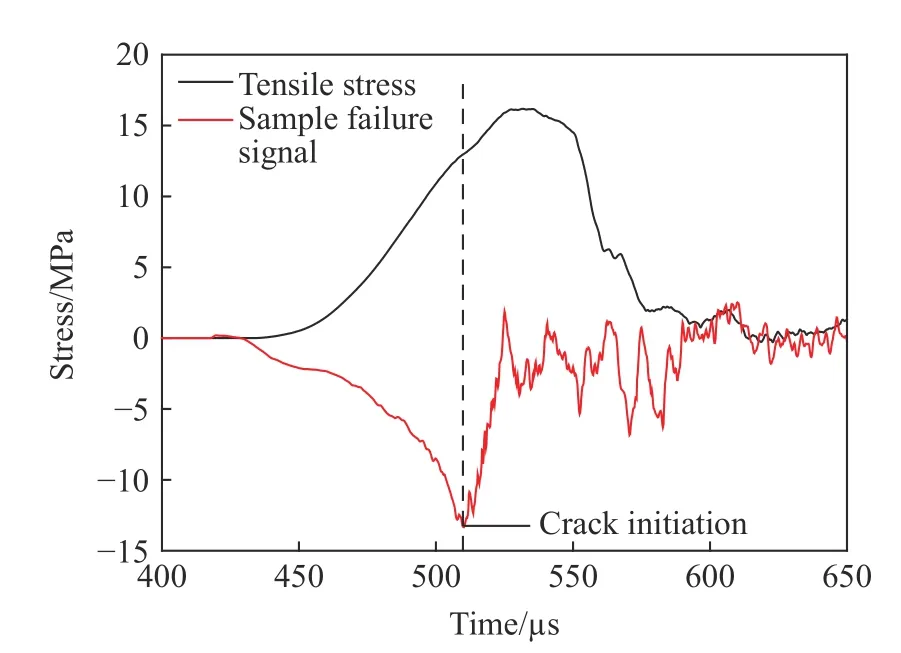
图16 345.3 GPa/s 加载率工况模拟结果过载修正Fig.16 The overload correction for numerical tensile stress under 345.3 GPa/s loading rate

图17 实验与数值模拟动态巴西劈裂实验过载比Fig.17 Experimental and numerical overload ratio for dynamic BD tests

3 结果分析及讨论

巴西圆盘实验中拉伸破坏首先发生在圆盘中心，此时圆盘的破坏符合格里菲斯破坏准则，据此得到了式（1）所示静态条件下巴西劈裂拉伸强度计算公式。根据格里菲斯破坏准则，式（1）中Pf对应的应当是圆盘中心起裂时刻的荷载，但在实践中，人们往往取圆盘破坏荷载进行计算。假设圆盘中心起裂以及峰值荷载（圆盘失稳）对应时刻分别为 t1和t2，显然 t1＜t2，同样地，对应的载荷也有P (t1)＜P(t2)。Mellor 等[13]认为，虽然圆盘试样中心点处已经发生了拉伸破坏，但试样的承载能力仍继续增加，因此直接采用圆盘峰值荷载计算得到的拉伸强度应较真实值偏大。

图18 609.6 GPa/s 加载工况数值模拟中的过载现象以及圆盘破坏过程Fig.18 The overload phenomenon and the failure process of numerical specimen under 609.6 GPa/s loading rate

这里借助数值模拟的结果进一步讨论岩石在巴西圆盘实验中破裂的详细过程。在静态实验中圆盘裂纹扩展速率远大于加载速率，圆盘从起裂到失稳破坏经历的时间极短，因此在Δt=t2−t1时间区间内可以近似认为P(t1)≈P(t2)。可以认为近似静态加载条件下使用式（1）计算得到圆盘的名义拉伸强度等于其真实拉伸强度。

与准静态实验不同，动态实验加载速率高（通常在几十到上千GPa/s）。虽然在动态圆盘实验中，圆盘起裂到整体失稳的持续时间Δt 只有微秒的量级，但在Δt 时间区间内，试样端部拉伸应力的增长却是不容忽视的。

图18 中给出了数值模拟得到的609.6 GPa/s加载工况下动态巴西圆盘实验结果。如图18 所示，在圆盘拉伸应力时程曲线上取4 个特征时刻（A、B、C、D），并给出各时刻对应的试样竖向速度云图，其中：时刻A 应力波传至入射杆右端，时刻B 和C 分别对应圆盘中心起裂以及裂纹扩展至试样端部，在时刻D 圆盘完全失稳。分析图18可以发现，在圆盘中心起裂（时刻C）后历时约20 µs 后才形成贯通的径向裂纹（时刻B），期间圆盘承载能力随裂纹向两端的扩展不断增加（圆盘拉伸应力从22.10 MPa 增加到26.77 MPa）。如果加载率进一步提高，可以预见过载效应会更加明显，这与本文实验得到的加载率越高名义拉伸强度与真实拉伸强度的偏差越大的结果相一致。

如果使用名义动态拉伸强度作为岩石材料动态拉伸强度，则会高估其真实强度，这将不利于认识动态荷载作用下岩石材料的固有拉伸强度。因此，建议在开展动态巴西圆盘实验时使用本文中方法进行拉伸强度过载修正，以获取岩石材料的真实动态拉伸强度。

4 结 论

借助SHPB 实验以及颗粒流程序数值模拟，研究了房山花岗岩动态巴西劈裂实验中拉伸强度的过载现象以及率相关性，通过设置应变片实现圆盘中心起裂时刻监测，对动态劈裂拉伸强度的过载特性进行了定量分析和校正，讨论了过载现象产生的物理机制。主要结论如下：

（1）动态巴西圆盘实验得到的岩石拉伸强度存在明显的过载现象，试样中心起裂时刻应力为真实拉伸强度，实验加载率越高，通过试样峰值应力确定得到的拉伸强度（名义拉伸强度）与岩石真实拉伸强度的偏差越大，过载效应越明显；

（2）利用PFC 程序进行数值验证时，引入实验名义拉伸强度率相关性结果对数值模型参数进行修正，通过对比实验以及数值模拟观测到的动态拉伸强度的过载现象以及率相关性，进一步证明动态巴西圆盘测试方法中过载现象的存在；

（3）基于格里菲斯破坏准则明确了巴西圆盘实验计算强度时采用荷载的物理意义，讨论了巴西圆盘方法中真实拉伸强度与对应的圆盘构型承载力的区别，认为动态巴西圆盘实验过载现象产生与圆盘构型以及高加载率有关；

（4）因为高加载率下过载比高达40%，所以认为有必要在动态巴西圆盘实验时进行过载修正，以获取岩石材料的真实动态拉伸强度。