基于钽球缺药型罩的多模式毁伤元成型规律
郭洪卫, 张浩宇, 张树凯,李 元,张郑伟,贾宪振, 刘瑞鹏
(1. 北京理工大学 爆炸科学与技术国家重点实验室,北京 100081; 2. 西安近代化学研究所,陕西 西安 710065; 3.吉林江北机械制造有限责任公司,吉林 吉林 132021)
引 言
钽药型罩具有高密度、高熔点、高延展性等优点,因此国外学者对钽药型罩在聚能装药中的应用开展了大量的研究[1]。Bergh等[2]通过X摄像验证了钽可形成EFP的可行性;Kim等[3]研究了药型罩厚度对钽EFP成型的影响,得到了钽EFP头部速度、长径比以及最小直径与药型罩厚度的变化关系;樊雪飞等[4]测试了钽的材料动力学性能,并开展了钽的弧锥结合罩的多模式战斗部研究;郭腾飞等[5]研究了基于钽材料的弧锥结合罩结构参数对毁伤元成型的影响;朱志鹏等[6]对大长径比钽爆炸成型弹丸进行了正交优化设计,得到长径比为4.76的钽EFP,比相同条件下铜的侵彻性能更强。从以上研究可以看出,目前国内外针对钽药型罩的研究集中在弧锥结合罩,而针对钽材料球缺药形罩的毁伤元成形特性却报道较少。通过改变战斗部的起爆方式可使球缺药型罩形成普通EFP和长杆型EFP,实现两种毁伤元的模式转换,具有较高的军事应用价值,有必要研究钽球缺药型罩多模式毁伤元的成型规律,寻找可形成较优侵彻体的药型罩结构参数。
本研究基于爆轰波碰撞理论和马赫杆高度计算模型分析了起爆半径对毁伤元成型的影响,在此基础上利用LS-DYNA有限元程序研究了不同结构钽药型罩的两种毁伤元成型结果,给出毁伤元参数变化规律以及药型罩结构参数,以期为钽EFP多模式战斗部设计提供参考。
1 爆轰波碰撞的理论模型
在聚能装药战斗部进行多点起爆时,相邻的爆轰波首先发生正碰撞,两个强度相等的爆轰波发生反射,可视为其中一个爆轰波对刚性壁面的正反射[7]。爆轰波以较小的入射角入射到刚性壁面上时,波阵面在固壁上发生正规斜反射,如图1所示,其中I为入射冲击波,R为反射冲击波,ψ为爆轰波入射角,φ为反射角,爆轰波波后产物从(0)区流动到(1)区的偏转角θ1与从(1)区流动到(2)区的偏转角θ2相等,即θ1=θ2=θ。入射波后的(1)区中各参量为:
(1)
式中:pH、uH、ρH分别为(1)区中爆轰产物的超压、流动速度和流动密度;ρ0为凝聚炸药的密度;D为爆速;k为绝热指数。沿着爆轰波入射波阵面流动的速度前后不变,由图1的几何关系可得:
(2)
爆轰波碰撞过程满足动量守恒和能量守恒,根据守恒关系结合爆轰波反射的几何关系可以推导出入射角ψ和偏转角θ、反射角φ的关系:

(3)
(4)
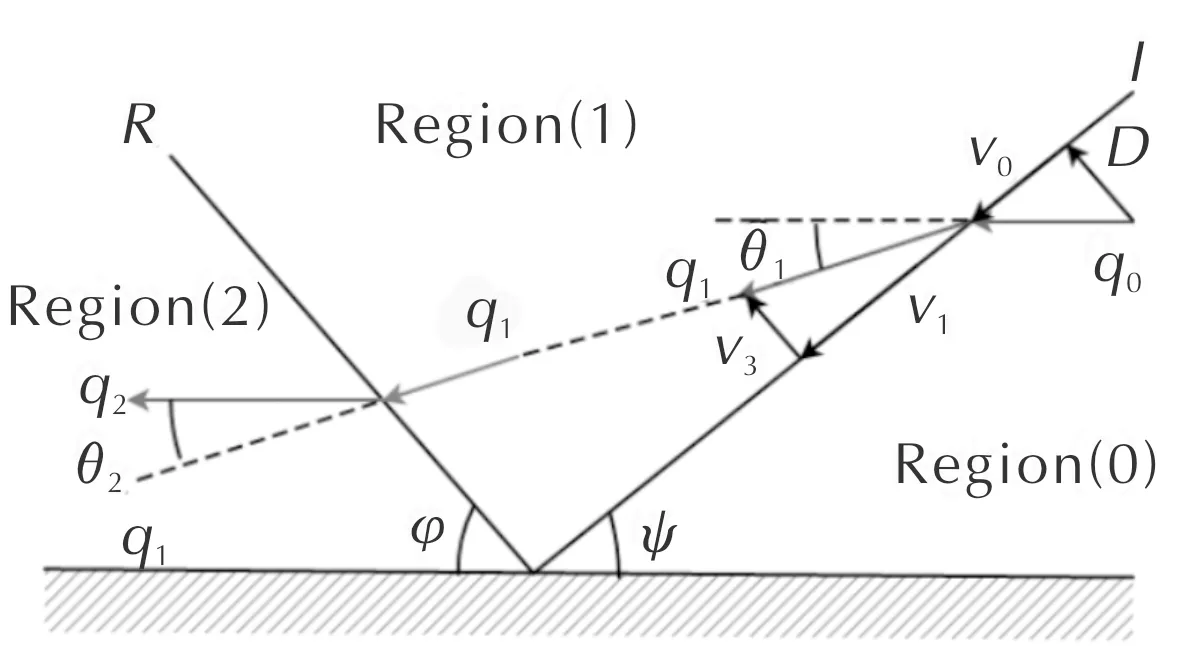
图1 爆轰波的正规斜反射Fig.1 Regular oblique reflection of detonation wave
给出不同时刻的入射角ψ,根据式(2)和式(4)可以迭代求出偏转角θ和反射角φ,将反射角和偏转角再带入式(3)即可求得正规斜反射中不同入射角下的反射区压力p2。
当爆轰波入射角增加到一定值时,偏转角θ2逐渐小于θ1,反射波从固壁上脱离,随着粒子流的不断积累,迫使碰撞点发生偏离,形成马赫杆。假设超压爆轰释放的能量Q3与C-J爆轰释放的能量Q的比值为ε,可计算出马赫区的超压p3:
(5)

(6)
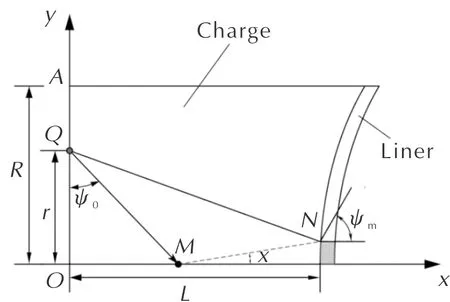
图2 爆轰波传播示意图Fig.2 Diagram of detonation wave propagation
由于假设马赫增长角在马赫波成长过程中保持不变,因此三波点轨迹为直线,根据图2的几何关系可得出简化后的马赫高度计算公式为:

(7)


图3 马赫高度随爆轰波传播距离计算结果对比Fig.3 Comparison of calculation results of Mach height with detonation wave propagation distance
2 战斗部结构及计算模型
2.1 有限元模型的建立
本研究的战斗部结构及尺寸如图4所示,战斗部装药直径Dk为100mm,装药高度H为100mm,壳体厚度S为5mm,药型罩外曲率半径R1、内曲率半径R2和药型罩壁厚d作为研究变量。

图4 战斗部示意图Fig.4 Diagram of warhead
采用有限元程序LS-DYNA建立二维轴对称模型,包括炸药、空气、药型罩及壳体4部分。空气、炸药和药型罩使用多物质ALE算法,壳体使用拉格朗日算法,通过流固耦合算法定义其相互作用,网格尺寸为0.6mm。炸药为JH-2,使用高能炸药材料模型和JWL状态方程,药型罩和壳体材料分别为钽和45#钢,使用Johnson-Cook本构模型和Grüneisen状态方程,具体材料参数见文献[4]。为了更完整地呈现毁伤元形态,在计算到200μs时将毁伤元从二维重映射到三维模型。
为方便后续的研究,给出毁伤元性能参数的定义[11],如图5所示,其中Ls为毁伤元的有效长度,Le为毁伤元的总长,De为毁伤元的最大直径;长径比用Le/De表示,密实度用Ls/Le表示。

图5 毁伤元性能指标Fig.5 Performance parameter of penetrator
2.2 起爆半径的选择
药型罩曲率半径R1和R2为100mm、108mm,药型罩壁厚d为4mm,可计算得到药型罩顶端与炸药端面距离L为86.6mm,此时装药半径L>Rtan44.8°,起爆半径r由0增大到装药半径R时,炸药中心处的爆轰波在压垮药型罩时均会发生马赫反射。由式(1)~式(6)迭代可计算出不同起爆半径下压垮药型罩时的马赫参数,如图6所示。

图6 马赫超压和马赫高度随起爆半径的变化Fig.6 Variation of Mach overpressure and Mach height with initiation radius
由图6可以看出,随着起爆半径的增加,压垮药型罩的马赫超压值p3越大,马赫杆高度h逐渐降低。为权衡马赫超压和马赫杆半径对毁伤元成型形态的影响,分别设置起爆半径r为0(中心单点起爆)、0.2R、0.4R、0.6R、0.8R、1.0R。
图7为不同起爆半径下毁伤元的成型参数。由图7可以看出,随着起爆半径r的增大,毁伤元头部速度、长径比逐渐增大,密实度逐渐减小。当起爆半径由0增加到1.0R时,毁伤元头部速度增加了18.7%,长径比增加了106.9%,密实度减小了33%。当起爆半径为1.0R时,毁伤元头部中心出现中空,这主要是由于起爆半径较大时,马赫波以较大的超压作用于较小面积的药型罩微元,使得毁伤元头部的局部速度过高,导致头部出现中空甚至断裂,进而导致毁伤元的飞行稳定性和侵彻能力降低。观察毁伤元成型的结果可以发现,当起爆半径为0时可形成密实度为1且长径比为1.4的EFP,当起爆半径大于0.4R时可形成密实度为0.65~0.8且长径比大于2的杆式EFP。因此综合考虑毁伤元形态、速度以及长径比,在后续的研究中使用起爆半径为0(中心单点起爆)和环起爆半径为0.8R两种起爆方式,本研究将中心单点起爆形成的毁伤元叫EFP,起爆半径为0.8R形成的毁伤元叫杆式EFP。
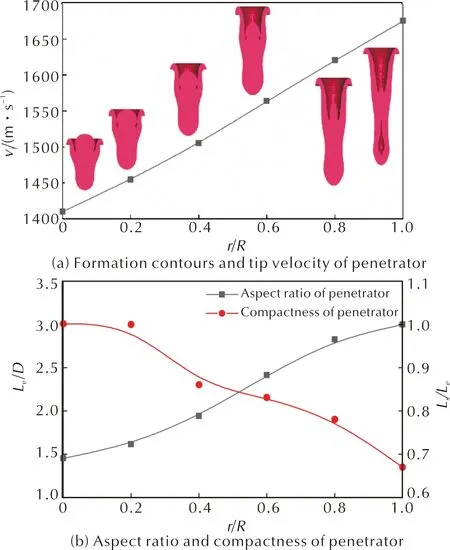
图7 毁伤元成型指标随起爆半径的变化曲线Fig.7 Variation curves of forming parameter of penetrator with initiation radius
3 药型罩结构参数对钽毁伤元性能的影响规律
3.1 药型罩内曲率半径对钽毁伤元的影响
选取药型罩壁厚d为4mm,药型罩外曲率半径R1为100mm,将药型罩内曲率R2分别设置为1.0R1~1.12R1(增量为2mm),其中R2取1.0R1时药型罩为等壁厚球缺药型罩。图8为不同内曲率半径时的药型罩半模型结构对毁伤元成型参数的影响。由图8可以看出,随着内曲率半径的增大,药型罩中心壁厚不变,药型罩边缘处壁厚逐渐变薄,因此改变内曲率半径本质上是改变了药型罩边缘壁厚。
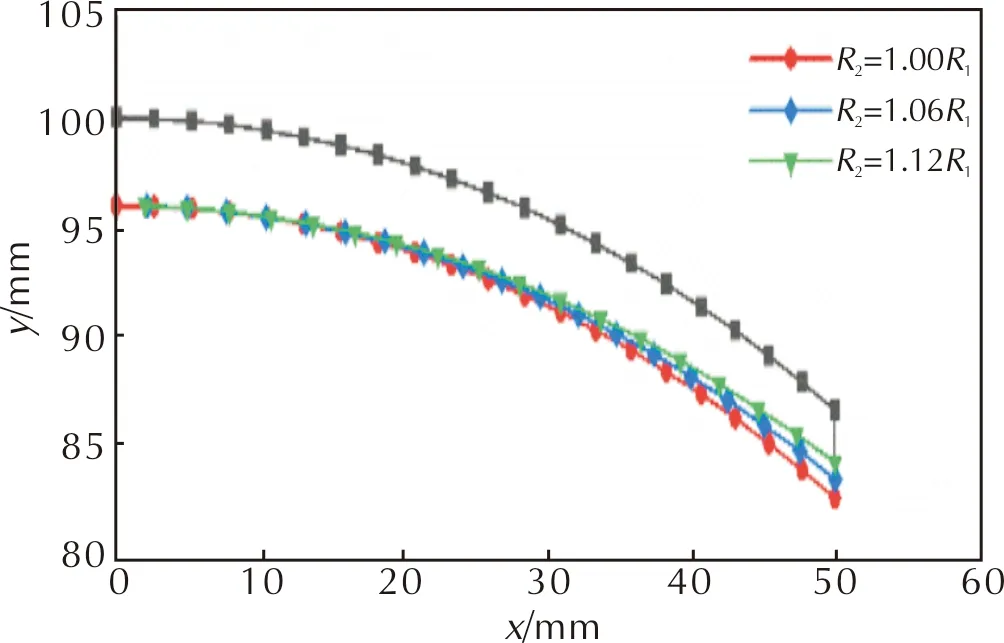
图8 不同内曲率半径R2时的药型罩结构对毁伤元成型参数的影响Fig.8 Influence of liner structure on the forming parameters of penetrator with different inner radius curvature R2
图9为毁伤元参数随药型罩内曲率半径的变化关系。

图9 毁伤元性能指标随内曲率半径R2的变化曲线Fig.9 Variation curves of penetrator performance parameter with inner curvature radius R2
由图9可以看出,当内曲率半径由1.0R1增加到1.12R1时,EFP和杆式EFP头部速度分别增加12.7%、5.2%,密实度分别增加46%、86%,EFP和杆式EFP的长径比变化较小。当R2大于1.08R1时,EFP毁伤元尾部突出,尾部质量高于头部质量,在飞行过程中极易发生翻转,导致飞行稳定性较差。当R2小于1.04R1时,杆式EFP的头部质量较少,导致侵彻能力降低。因此综合考虑,选取内曲率半径R2为1.04R1~1.08R1。
3.2 药型罩外曲率半径对钽毁伤元的影响
选取药型罩壁厚d为4mm,药型罩内曲率半径R2为106mm,将药型罩外曲率半径R1分别设置为0.906R2~1.00R2(增量为2mm)。不同外曲率半径R1时的药型罩结构对毁伤元成型参数的影响如图10所示。

图10 不同外曲率半径R1时的药型罩结构对毁伤元成型参数的影响Fig.10 Influence of liner structure on the forming parameters of penetrator with different outer radius curvature R1
由图10可以看出,随着外曲率半径的增大,药型罩边缘壁厚逐渐减小,并且由于药型罩的外壁与炸药接触,同时增大了炸药对药型罩边缘位置的压垮角。
图11为毁伤元性能指标随药型罩外曲率半径的变化关系。


图11 毁伤元性能指标随外曲率半径R1的变化曲线Fig.11 Variation curves of penetrator performance parameter with outer curvature radius R1
从图11可以看出,随着药型罩外曲率半径R1的增大,EFP和杆式EFP的头部由密实逐渐变为中空,且头部速度都逐渐减小,当外曲率半径由0.906R2增加到1.0R2时,EFP和杆式EFP速度分别减小13.3%、5.9%,密实度分别减小57%、90%,长径比先减小后趋于稳定。R1较大将导致毁伤元头部密实度较低,侵彻能力较低,R1较小将无法形成带尾裙的毁伤元,飞行稳定性较差,因此综合考虑毁伤元成型效果、头部速度、头尾速度差以及长径比等因素,选取药型罩的外曲率半径R1为0.925R2~0.962R2。根据上一节R2的选取范围取交集,则可以得出R1和R2的关系应为1.04 选取药型罩外曲率半径R1为100mm,药型罩内曲率半径R2为106mm,以装药直径Dk为参考,将药型罩壁厚d分别设置为0.032Dk~0.042Dk(增量为2mm),不同壁厚时的药型罩结构对毁伤元成型参数的影响如图12所示。 图12 不同壁厚d时的药型罩结构对毁伤元成型参数的影响Fig.12 Influence of liner structure on the forming parameters of penetrator with different thicknesses d 由图12可以看出,仅增大药型罩顶端壁厚d时,药型罩边缘壁厚也逐渐增加,由于内外曲率半径不变,因此爆轰波对药型罩的压垮角不变。 图13为毁伤元性能指标随药型罩壁厚的变化关系。由图13可以看出,当药型罩壁厚d由0.032Dk增加到0.042Dk时,EFP和杆式EFP速度分别降低22.9%、19.8%,长径比分别降低45.2%、33.7%,密实度分别降低12.0%、34.1%。当药型罩壁厚小于0.036Dk时,杆式EFP头部存在较多的中空,并且EFP的尾裙也逐渐消失,导致EFP的飞行稳定性降低,而当药型罩壁厚d较大时,毁伤元头部速度、密实度减小、长径比都减小,导致毁伤元的侵彻能力降低。因此综合考虑毁伤元成型效果、头部速度、头尾速度差以及长径比等因素,药型罩壁厚应选为0.036Dk~0.040Dk。 图13 毁伤元性能指标随药型罩壁厚d的变化曲线Fig.13 Variation curves of penetrator performance parameter with liner′s thickness d 综合考虑毁伤元速度、长径比以及密实度,根据上文中优化的结构参数范围,设置药型罩内曲率半径R2为106mm,外曲率半径R1为100mm(R2/R1=1.06),药型罩壁厚d为3.8mm(0.038Dk),毁伤元炸高为3倍装药口径,性能参数见表1。 表1 毁伤元性能参数 图14为两种毁伤元侵彻45#钢靶的结果。 图14 两种毁伤元侵彻结果Fig.14 Penetration results of two penetrators 从图14可以看出,EFP侵彻到靶板底部时逐渐堆积,形成二次扩孔,导致靶板底部侵彻孔径较大,杆式EFP在侵彻过程中毁伤元沿着靶板内壁流动,侵彻孔径比较均匀,EFP侵彻深度为89.1mm,杆式EFP侵彻深度为152.3mm,杆式EFP的侵彻深度较EFP侵彻深度提高71.9%。 (1)用爆轰波碰撞理论和马赫高度计算模型解释了不同起爆模式对毁伤元成型的影响,确定环形起爆半径时,需要权衡马赫超压和马赫杆高度两个因素,若起爆半径过大,则马赫波以较大的超压作用于较小面积的药型罩,导致毁伤元内部出现中空甚至断裂,降低侵彻能力。 (2)通过研究钽球缺药型罩的内外曲率半径和药型罩壁厚,发现毁伤元速度和密实度与药型罩内曲率半径呈正相关,与药型罩外曲率半径和药型罩壁厚呈负相关,毁伤元长径比与药型罩内外曲率半径以及壁厚呈负相关。 (3)钽球缺药型罩可形成多模式毁伤元,中心单点起爆和环形起爆均可形成较优的侵彻体,成型较佳时各结构参数的取值关系为:内曲率半径R1和外曲率半径R2的关系为1.043.3 药型罩壁厚对钽毁伤元的影响
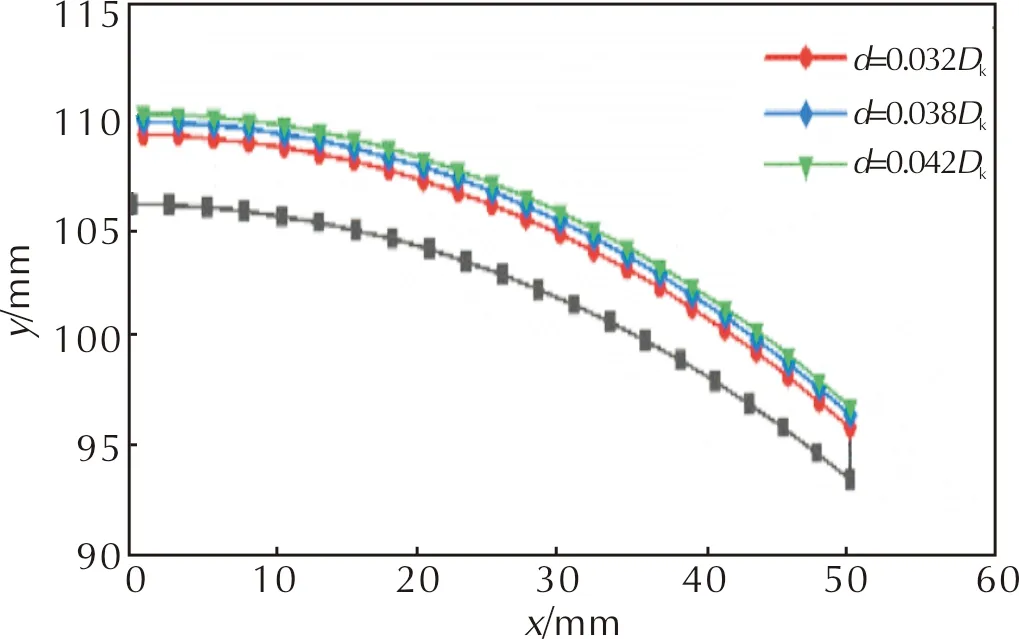
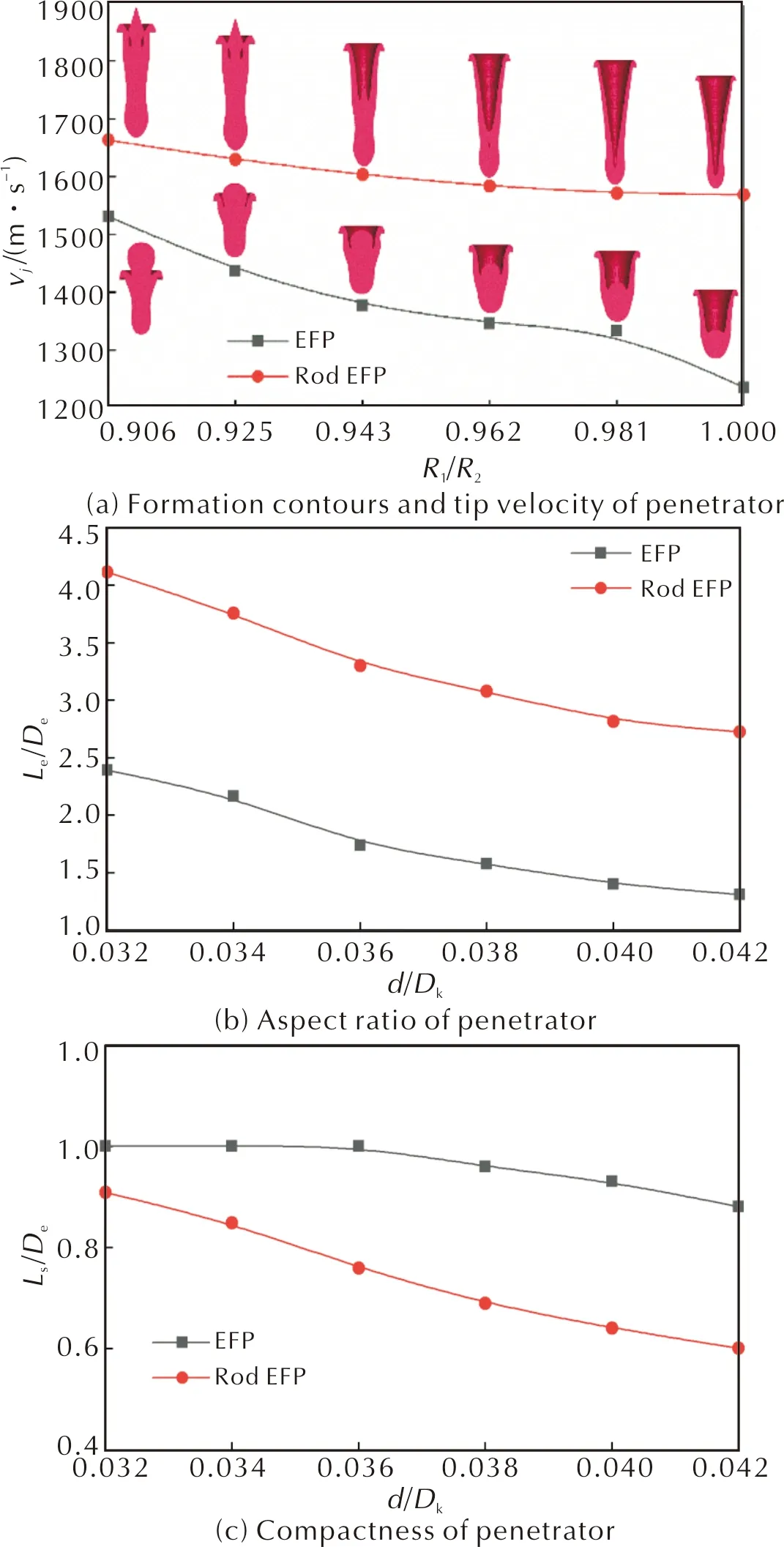
3.4 两种毁伤元侵彻能力对比

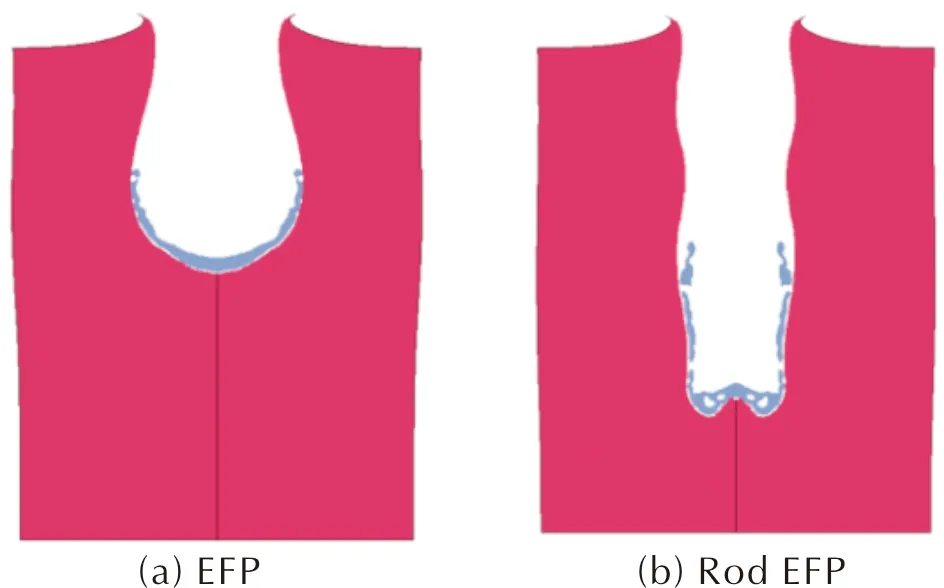
4 结 论

