一种含扰动项的非线性系统执行器故障估计方法*

孙延修

（沈阳工学院基础课部，辽宁 抚顺 113122）

0 引言

目前，控制系统对稳定性及可靠性的要求越来越高。如飞行控制系统，系统故障在飞行控制系统中会导致性能降低，甚至出现灾难性的后果［1］。因此，针对系统故障诊断进行研究具有重要的实际意义与应用价值。故障诊断及估计的方法已经取得了丰富的研究成果，过去几十年基于观测器对故障进行诊断与估计的方法有很多，如未知输入观测器、自适应观测器、滑模观测器和奇异观测器的方法［2-4］等。

近年来，基于观测器对故障诊断的研究中，针对不同类型的系统故障进行诊断也取得了一些积极的成果，如线性系统［5-6］、随机系统［7］、非线性系统［8-10］、广义系统［11］等。其中文献［5］考虑到系统干扰，针对含干扰项线性系统故障的估计进行了研究，提出了一种快速估计方法；文献［8］针对一类非线性系统研究了故障诊断观测器的设计问题，通过设计故障诊断观测器，利用线性矩阵不等式方法给出了系统渐近稳定的条件，使故障闭环系统满足一定的性能指标；文献［10］针对汽车稳定控制系统，利用李雅普诺夫理论设计了观测器，获得原系统状态与虚拟执行器故障的渐近估计；文献［11］针对含有执行器故障的广义系统，利用区间观测器实现了故障检测；文献［12］针对系统故障导数及系统干扰项上界未知的情形下进行了研究，提出一种故障诊断观测器，达到了良好的估计效果。

基于上述分析，本文针对一类含干扰项的非线性系统进行了研究，提出了一种执行器故障鲁棒估计方法。通过构造增广状态向量并设计增广状态观测器，对原系统中的执行器故障进行估计，在构造增广观测器的过程中考虑到原系统中的干扰项，通过借助技术消除了外部干扰对执行器故障估计的影响，达到了对原系统中执行器故障进行鲁棒估计的目的。

1 系统描述

考虑如下非线性系统：

通过观测器对原系统中的执行器故障进行估计。

2 增广观测器的存在性判据

2.1 系统不含外部扰动项Dω（t）的情况下观测器存在性判据

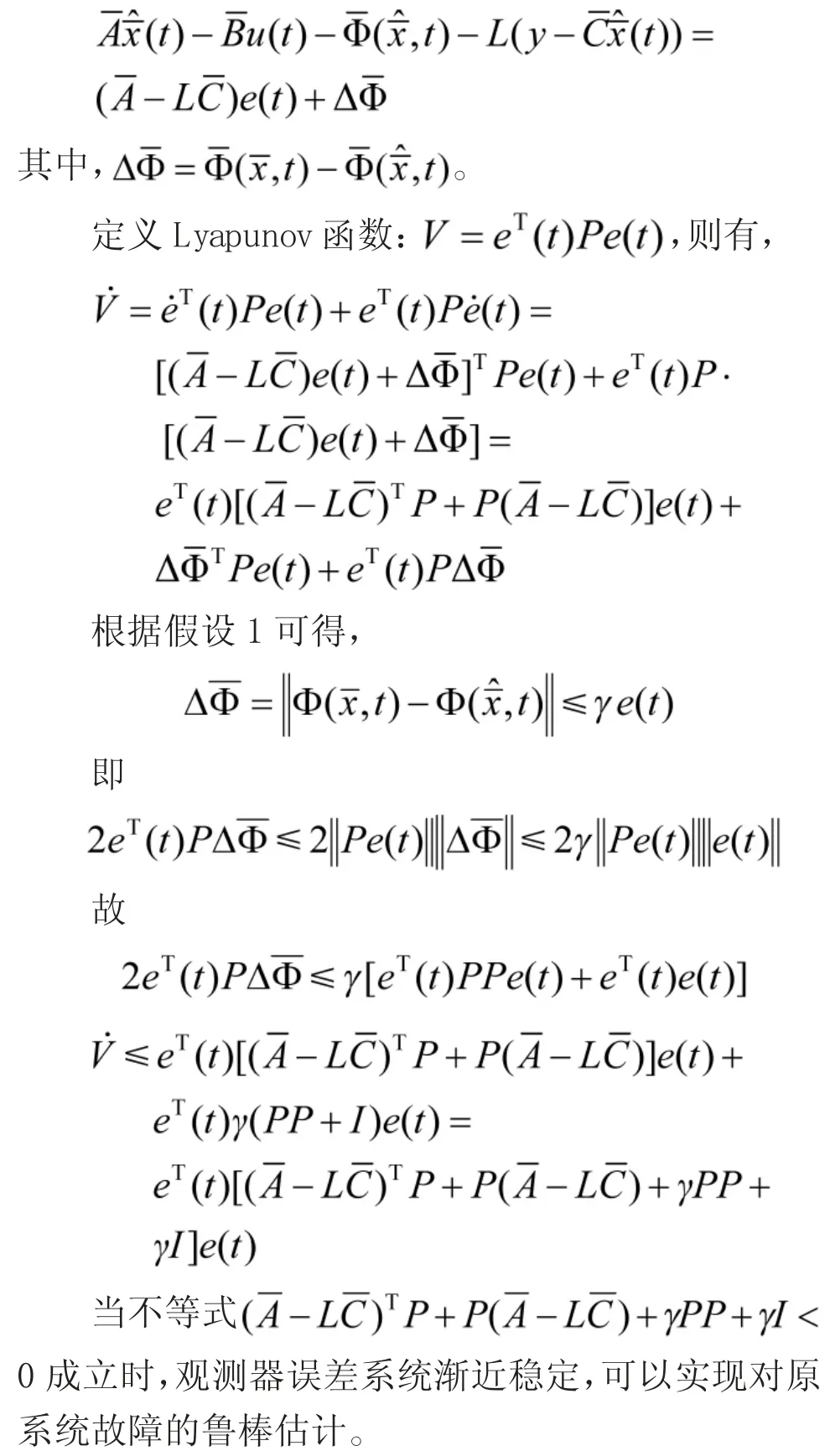
由Schur补引理1 知，不等式（4）成立时观测器误差系统渐近稳定，命题得证。

2.2 含有外部扰动项Dω（t）的情况下观测器存在性判据

定理2 针对非线性系统（1），若存在正定矩阵P 和增益矩阵L 使得如下线性矩阵不等式成立，

其中

由上述可知，当M＜0 时误差动态方程渐近稳定，可以实现对执行器故障的鲁棒估计。利用Schur补引理M＜0 等价于不等式（5），命题得证。

3 执行器故障的渐近估计

4 仿真算例

1）当系统不含扰动项时，应用MATLAB中的LMI工具箱求解线性矩阵不等式（4），计算出正定矩阵P 和观测器增广矩阵L 分别为：

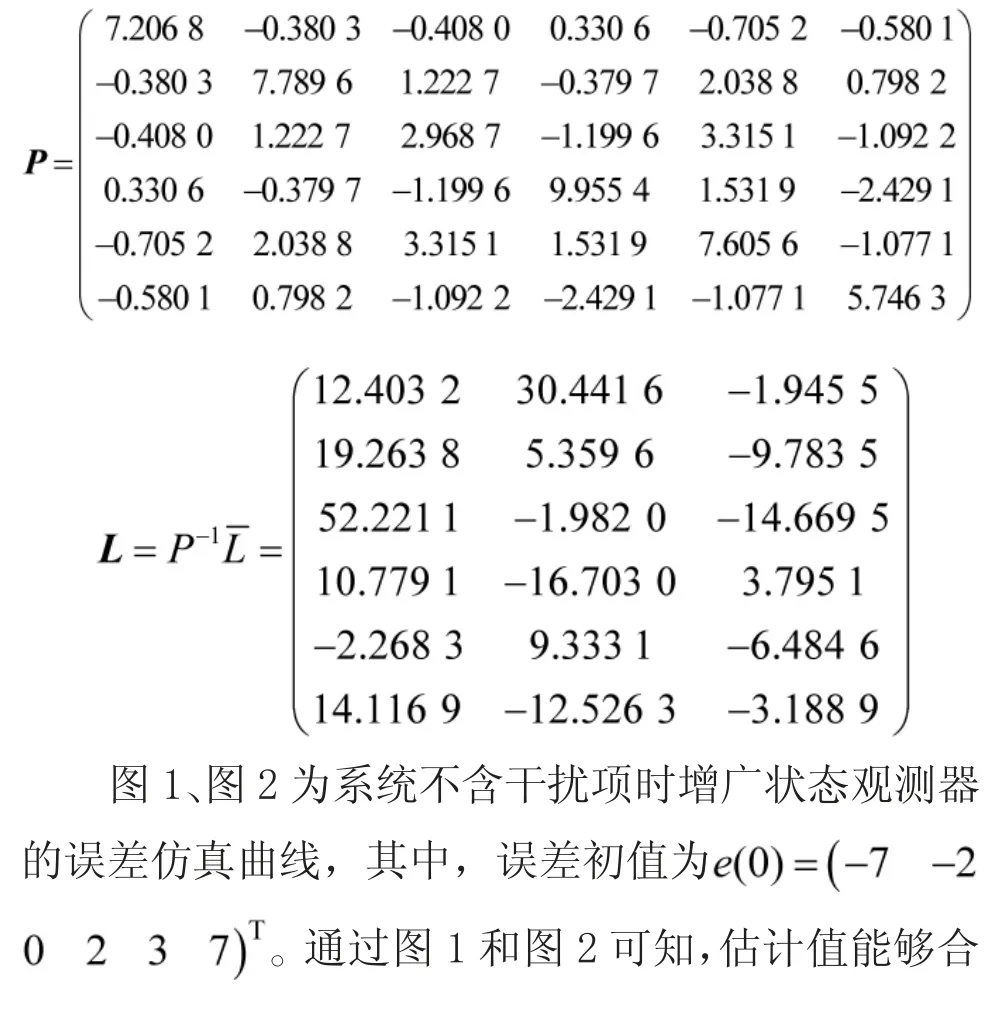
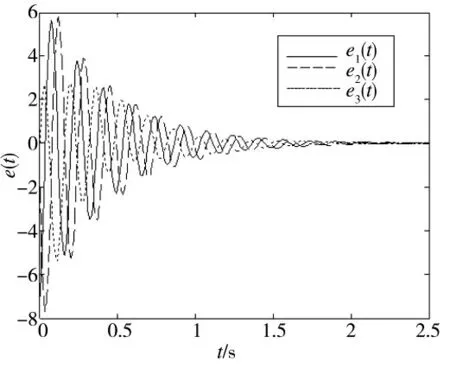
图1 无干扰时误差系统仿真

图2 无干扰时误差系统仿真

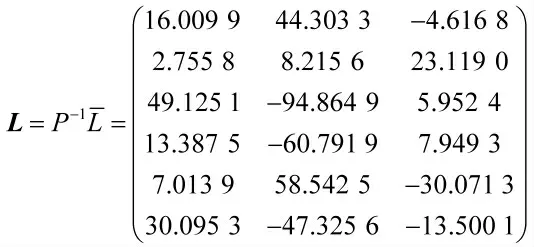
2）当系统中含有干扰项时，应用MATLAB中的LMI工具箱求解线性矩阵不等式（5），计算出正定矩阵P 和观测器增广矩阵L 分别为：

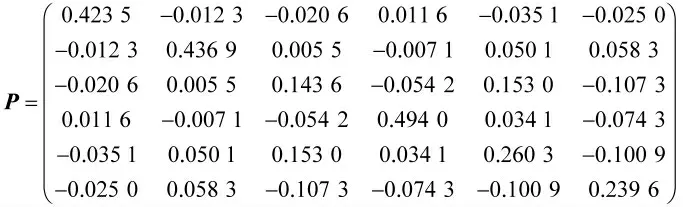
5 结论

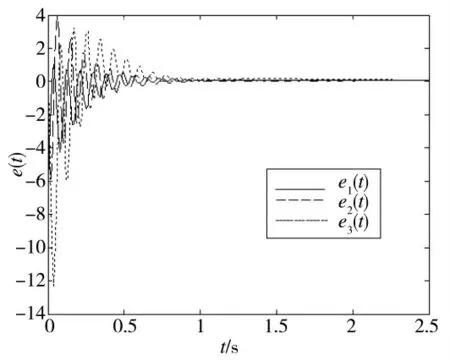
图3 系统含干扰项时误差系统仿真

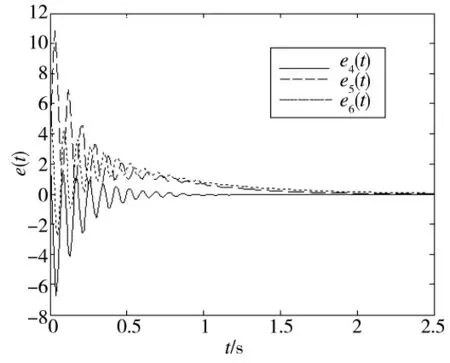
图4 系统含干扰项时误差系统仿真

本文针对一类存在干扰项的非线性系统，提出了一种基于增广状态观测器的执行器故障估计方法。通过Schur补引理以线性矩阵不等式的形式给出了观测器存在的充分条件，从而使观测器误差系统渐近稳定，可实现对执行器故障的鲁棒估计。针对非线性系统存在的干扰项，通过设定性能指标降低了系统扰动对执行器故障估计的影响，保证了执行器故障估计的有效性。