改进遗传变邻域算法求解飞机装配线调度问题

蔡 玮，赵 轶，陈浩杰，张 剑

（1.西南交通大学 先进设计与制造技术研究所；2.成都飞机工业（集团）有限责任公司成都，610000）

0 引言

飞机装配具有作业数量大、装配关系复杂等特点，且驾驶舱等部段区域可容纳资源的空间有限，所以飞机装配线作业调度问题可看作是一类具有特殊空间约束的资源受限项目调度问题[1]（Resource Constrained Project Scheduling Problem，RCPSP），该类问题已被证明为一类复杂的强NP-hard问题[2]，针对不同约束和目标的RCPSP建模及求解技术，国内外学者展开了大量的研究。

建模中，Elmaghraby和Kamburowski[3]对活动紧前紧后约束进行了归纳并提出了相应的建模方法，Slowinski[4]则从资源约束的角度对RCPSP建模，杨红光[5]等对双边装配线模型进行了研究，曹阳华[6]等考虑了U型装配线的生产效率模型并对该问题进行了求解，孙宝凤[7]等建立了混流装配线的双目标投产排序模型。从求解角度来看，解决RCPSP及其扩展问题的算法可分为三大类：精确算法、启发式算法和元启发式算法（智能算法），其中精确算法虽然能得到理论最优解，但仅适用于小规模求解，由此近似算法开始被应用于求解大规模RCPSP问题[8]。自1963年，Kelley[9]提出了调度生成方案后，在此基础之上各种启发式算法相继被提出，但其不具备优化能力，往往受到问题本身的影响而得不到满意解。元启发式算法和智能算法的应用使问题的求解得到了新的发展，如喻小光[10]等引入局部搜索中的模拟退火算法（Simulated Annealing，SA）来求解RCPSP，进化算法（如遗传算法[11]，Genetic Algorithm，GA）和群体智能算法（如蚁群优化算法[12]，Ant Colony Optimization，ACO）都在求解RCPSP问题上得到了广泛的应用。

飞机装配线调度问题属于传统RCPSP的扩展问题，其中作业活动除了受到紧前紧后约束和资源的约束外，在飞机的某些部段，众多满足资源的并行活动，常因空间的限制而无法同时进行，从而增加了问题空间和计算求解的复杂度。本文综合考虑作业活动紧前紧后、资源约束和空间约束，以最小化装配总工期为目标，建立了飞机装配线作业调度的数学模型，并针对遗传算法容易过早收敛的缺陷，提出了一种改进的遗传变邻域算法（Improved Genetic Algorithm Variable Neighborhood Search，IGA-VNS）用以求解模型。该算法采用RCPSP中两种较优的启发式规则，即最晚开工时间最小（EDDF）和最晚完工时间最小（MINLFT）[13]进行初始化以改善初始种群，结合考虑接受阈值的变邻域局部搜索来提高遗传算法全局搜索能力，设计了交叉、变异策略和三种邻域结构以避免在算法搜索过程中产生非法解，通过PSPLIB中的标准算例验证了算法的有效性。

1 问题描述及数学模型构建

1.1 问题描述

飞机装配过程是指飞机进入装配线到装配完成的一系列装配与测试活动，其调度问题可描述如下。一项飞机装配作业项目由活动集合J（J={0，1，2，…，n+1}）组成，其中活动0和n+1为虚活动，仅代表项目的开始和结束，不占用时间和资源。活动j（j∈J）的紧前作业集合用Pj表示，j的紧后作业集合用Sj表示。tj表示活动j的持续时间，sj表示活动j的作业开始时间。一项装配作业项目中的活动分属于飞机的不同部段，定义M为部段集合，M={1，2，…，z}，m∈M为部段号，Cm表示在部段m中的活动集合，ej表示作业活动j的空间占用量，各部段的最大空间容量为Nm。R（R={r1，r2，…，rq，…，rk}）表示装配过程中的k种资源集合，用rjq表示活动j对第q种资源单位时间的需求量，bq为资源q单位时间的最大供应量。对时间进行离散化处理，d={1，2，…，T}为离散的时间节点，T表示装配作业总工期，Ad={j|stj＜d stj+tj}为d时刻正在执行的作业活动集合。

1.2 数学模型构建

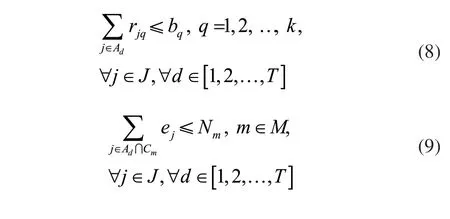
其中：式(1)为目标函数，即最小化装配作业总工期；式(2)为决策变量；式(3)表示每项作业活动必须在其规定持续时间完成；式(4)表示活动j一旦开始则在完成之前不能中断；式(5)和(6)表示虚活动0和n+1的持续时间和资源需求量都为0；式(7)为活动紧前紧后约束，活动j必须在其全部紧前活动完成后才能开始；式(8)为资源约束，d时刻正在执行的所有活动对某种资源的需求量不大于该资源单位时间的最大供应量；式(9)为各部段的空间约束，d时刻在部段m中正在执行的所有活动对空间的需求量不大于部段m的最大空间容量。

2 遗传变邻域算法设计

2.1 遗传变邻域算法策略及流程

由于遗传算法存在容易陷入局部最优的缺陷，本文设计了一种结合接受阈值的变邻域算法进行局部搜索，并设计交叉、变异策略和三种产生合法解的邻域结构以确保算法的进行和提高搜索能力，其主要算法步骤如下：

步骤1：参数设置。设最大代次数为maxGen；种群规模为popSize；交叉概率为Pc；变异概率为Pm。

步骤2：种群初始化。采用整数编码的方式产生popSize个染色体，并采用优先级规则对部分个体进行初始化。

步骤3：计算个体适应度值，并判断当前迭代次数gen是否达到最大迭代次数maxGen，若达到最大迭代次数则输出最优解；否则转步骤4。

步骤4：选择。采用锦标赛选择的策略从初始种群中选择部分个体。

步骤5：交叉。根据交叉概率Pc采用一种考虑紧前紧后的交叉策略对选择过后的染色体随机进行交叉操作。

步骤6：变异。根据变异概率Pm采用一种右移变异的策略对选中的个体进行变异操作产生新的种群newPop。

步骤7：变邻域操作。从newPop中选择适应度值前20%的个体作为变邻域操作的初始解集S，变邻域操作后生成局部最优解集。

步骤8：将局部最优解集重插入到原种群中，转步骤3。

图1 IGA-VNS算法流程

算法流程图如图1所示。

2.2 算法设计

1）编码设计与种群的初始化

该方法采用整数编码的方式进行编码，考虑每个活动的紧前紧后关系，例如染色体A=（0，1，2，…，n+1）中共包含n+2个活动，其中0和n+1代表开始和结束的虚活动，1，2，…，n代表了活动的调度顺序且满足紧前紧后关系。由于考虑到求解目标为最小化项目工期，本文选择两种较优的优先级规则（EDDF和MINLFT）初始化部分个体，其余个体采用随机初始化以提高初始种群的多样性，采用优先级规则进行初始化有效的提高了初始解的质量，从而缩小解空间。

2）解码设计

解码则为将编码基因转化为一个可行的调度，由此在解码过程中则需要考虑资源与空间约束的限制，即根据基因的顺序以及每个基因对应的活动对资源与空间的需求量，校验以保证在活动持续时间内每一时刻均满足资源的供应和空间限制，从而计算每项活动的开始时间和完工时间，而最后一项虚活动的开始时间即为装配作业总工期。

3）适应度函数设计

选用目标函数的倒数1/T乘以系数C作为适应度函数，既Fitness=C/T（C为常常数），则适应度函数值越大的个体在群体中其解越优。

4）选择

采用锦标赛选择策略对个体进行选择，每次从种群中随机选择一定数量的个体，根据其适应度函数值选择其中最优的个体进入新种群，并重复此操作直至选择出的新种群规模达到初始种群的90%。

5）交叉

在单点交叉的基础上进行了改进，形成了考虑紧前紧后关系的交叉策略。从父代取两个个体进行交叉，分别为M1和M2，取随机整数m作为断点，1≤m＜n，则可以得到两个子代C1和C2。子代C1的活动序列中，i=1，…，m的部分来自于父代M1，而i=m+1，…，n的部分来自于父代M2，但在这部分序列中，已经从父代M1中选择的活动将不再被考虑，这样的操作保证了父代中的活动优先顺序得以被保留且每个活动只出现一次，所产生的子代个体不会出现非法个体，子代C2的产生同理可得，便得到了两个新的子代个体。按照交叉概率pc进行以上的交叉操作得到与原种群规模相同的新种群。

6）变异

以变异概率pm对遗传算子的基因型做变动，采用了一种右移变异的策略，考虑某一个体的活动序列λ={1，2，…，i，…，n}，i为随机选择的活动，现将i所在位点右移到某一位置产生新一代个体，为了使新个体的活动序列仍然符合活动的优先级循序而不产生非法解，在右移之前需要判断该活动最小的可右移位置，即不破坏原有的紧后关系，而由于是将活动右移，所以其紧前活动仍然有效，从而得到新的个体λ’={1，…，i-1，i+1，…，h-1，i，h，…，n}，h所在位置即为i最小的可右移位置。以上的变异操作按照变异概率pm进行产生下一代的种群。

7）变邻域搜索操作

变邻域搜索的关键在于邻域结构的设计，但由于本问题中个体编码受到活动间优先级顺序的约束，常用邻域动作如插入、交叉等不适用于该问题的求解，会产生不满足优先级顺序的非法解，对非法解进行修正不仅增加了算法的复杂程度，而且影响运行效率。本方法借鉴之前所述的变异操作中右移变异的策略，设计了3种不会产生非法解的邻域结构，具体如下：

随机选择个体基因中的某一位点，根据活动的紧前紧后关系，记录该位点上对应活动的所有紧前活动在该项目列表中最大的下标位置，及该活动的所有紧后活动在该项目列表中最小的下标位置。1）将该基因右移插入到紧后活动最小下标位置前一位，构成第一种邻域结构；2）将该基因左移插入到紧前活动最大下标位置后一位，构成第二种邻域结构；3）将该基因随机插入到最小下标位置与最大下标位置之间，构成第三种邻域结构。

三种邻域结构具体示例如图2所示。在染色体F中随机选择基因位点G，G对应活动5的所有紧前活动中最大的下标位置为G1，其所有紧后活动中最大的下标位置为G2，则邻域结构1将活动5插入到P1位置得到新个体F1，邻域结构2将活动5插入到P2位置得到新个体F2，邻域结构3将活动5随机插入到P1和P2的中间位置P3或P4，得到新个体F3或F3’。

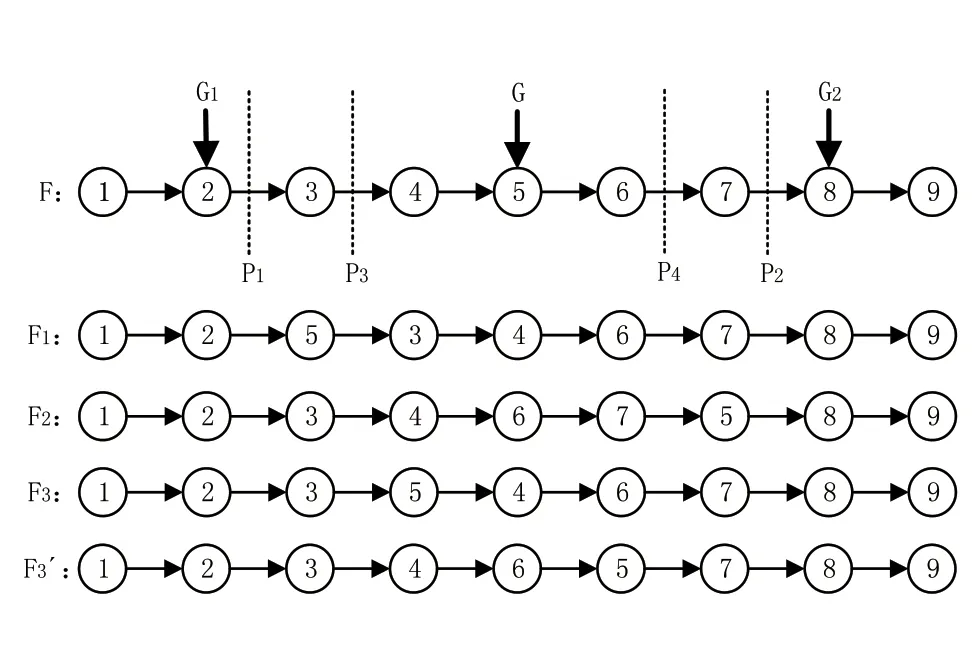
图2 邻域操作示例

除了邻域结构的设计，考虑到邻域搜索这种基于精英保留的策略仍然有陷入局部最优的风险，提出一种接受阈值的计算方法，即在接受阈值内考虑是否接受变邻域搜索得到的最优解，设变邻域搜索的初始解为s，目标函数值为f（s），经过邻域搜索后得到的新解为s’，目标函数值为f（s’）。当得到的新解优于初始解，即f（s’）-f（s）＜0时，以概率p=1接受新解，令s=s’进入下一步迭代；当得到的新解劣与初始解时，即f（s’）-f（s）＞0时，以概率p=exp{-[f（s’）-f（s）]/f（s）}接受劣解，令s=s’进入下一步迭代。

3 数值实验设计与结果分析

3.1 实验设计

为验证本文提出算法的可行性与有效性，采用标准算例库PSPLIB中的算例进行，即分别在活动数量为30、60、90的3种工况下随机选取5组初始输入数据。每种规模下的作业项目共享4种资源，每种资源设有单位时间最大的供应量，每项活动需要到一种或多种资源。随机选择某一种资源作为空间需求量，对于每种工况随机生成部段数[1，z]，并将活动随机分配到各部段中，部段的最大空间容量Nm为在该部段执行的活动中对空间需求量的最大值与作为空间需求量的资源的单位时间最大供应量之间的随机整数。通过Matlab2014b平台进行数值实验，采用IGA-VNS与传统遗传算法（GA），变邻域算法（VNS）和遗传模拟退火算法（GASA）进行对比，在每种工况下运算5次，得到的实验结果如表1所示，其中Duration表示装配总工期的均值，GAP为差值百分比。

式(5)中，T1为其他算法得到的总工期均值，T2为IGA-VNS算法的到的总工期均值。

3.2 结果分析

数值实验结果如表1和图3所示。实验结果表明，在不同作业规模下，基于IGA-VNS算法求解的飞机装配线调度问题的结果均优于其他三种算法，在活动数量为30的规模下，IGA-VNS比其他算法的目标值在精度上平均提高4.69%。当活动规模增大后，IGA-VNS的优势也不断扩大，在活动数量为60的规模下，IGA-VNS与其他算法的目标值在精度上平均提高4.89%，在活动数量为90的规模下，IGA-VNS比其他算法的目标值在精度上平均提高9.84%。且IGA-VNS较GA与VNS的求解能力具有明显优势，对于同样具有全局与局部搜索能力的GASA也有一定的优势。

5 结语

本文考虑飞机装配线受到空间限制的实际工程背景，同时考虑活动紧前紧后关系、资源约束与空间限制，建立了以最小化装配作业总工期为目标函数的飞机装配线作业调度数学模型，并设计了一种改进的遗传变邻域算法对该问题进行求解。数据实验表明，本文中所提出的算法比其他三种智能算法的求解结果更加优异，且随着规模的增加其优势更加明显，由此说明了该算法的有效性。为了更贴近飞机装配线实际调度，下一步将考虑将此算法应用至多工程项目调度问题和考虑资源和人员的动态变化所带来的影响。

表1 3种规模下的实验结果

图3 不同算法完工时间比较