基于多几何特性的产品质量综合评定方法研究

杜福洲，郭瑞振，李 群，官 威

（1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.沪东重机有限公司，上海 200129）

0 引言

几何特性是一组与产品几何状态相关的特性，是质量评定的重要内容，对产品功能、可靠性等有直接影响，可用来分析质量波动及追溯质量问题源头，以及为产品验收提供依据。

目前，国内外已建立了较为完善的产品几何公差设计与检验规范，细化了产品质量保证的具体要求。新一代GPSISO/TS 213针对产品设计与制造而制定了一系列几何技术规范，从源头上实现设计、制造、检测之间的协调与统一[1]。ISO9000[2]系列国际标准建立了质量管理体系，ISO9001标准是对质量要求、质量管理的具体和细分，并提出了相应的指标[3]。随着GPS的发展，国内外针对产品的形位误差评定体系也不断取得进展。英国的泰勒 霍普森参与了ISO标准的制定，并将相关技术应用于圆柱度仪检测产品的设计[4]。江平宇[5]基于模块化设计思想和优化算法，设计了几何公差评定系统，研究了几何数据分析与CAD系统的集成方法，实现了对误差评定结果的可视化。张玉[6]等基于最小二乘方法完成了对平面度和直线度的误差评定，并通过正交化处理简化了求解过程。卓兴仁[7]研究了圆度误差评定的4种方法，并进行了对比。

随着CAD/CAM/CAQ技术的发展与深入应用，设计、制造理论及应用技术也发生了诸多变化，对产品几何特性的检测与质量评定提出了新的要求。膝裕昌[8]基于系统工程理念，将模糊数学方法应用在了工程产品质量评定问题中，构建了综合评定数学模型，并针对推土机进行了质量评定体系的验证。谭健[9]采用定量与定性评定相结合的方法，针对转向架的装配工艺质量，建立了优化数学模型，形成了基于人因仿真的装配工艺质量评定体系。宋芒果[10]将模糊评定思想应用于DLG数字产品质量评定中，确定了评定指标及其重要系数。

综上所述，目前国内外产品质量评定研究与几何特性质量研究相对独立，较少将几何特性与产品质量要求建立关联，难以从综合的角度对产品质量进行评定，用于评定几何状态复杂且质量要求多样化的产品，有一定的局限性，未能考虑几何特性与产品质量的联系，也难以定量描述产品质量满足要求的程度。因此迫切需要合理的评定方法，既能够充分体现各几何特性对产品质量的影响，又能以定量的形式描述产品整体质量。本文从多几何特性出发，对产品的综合质量评定方法进行研究，构建了基于多几何特性的质量综合评定框架，在基于MBD的质量评定数据集构建、评定指标体系与权重设计、模糊评定数学模型建立等方面进行了研究，并讨论了其中的关键技术。

1 基于多几何特性的质量综合评定框架

构建基于多几何特性的质量评定总体框架，对质量评定数据集、基于模糊理论的质量评定体系、单件与批次产品质量评定进行研究。基于多几何特性的质量综合评定总体框架如图1所示。总体框架自下而上分为三个层次：基于模型定义层、质量评定指标体系层、综合评定层。基于MBD模型实现对产品数据的统一管理，包括几何信息和非几何信息，同时基于结构规范树实现数据存储与应用，产品几何特性以三维标注及其关联的几何特征进行表达[11]。

质量评定指标体系层中，包括评定指标体系和模糊评定数学模型。基于实际生产过程、生产经验、市场需求等因素，赋予评定指标相应的权重系数。构建质量综合评定数学模型，解算产品质量评定结果，同时根据多件产品质量评定结果，可以查看质量波动情况，映射到相应的生产过程中，判断产品生产过程是否可控、稳定，从而发现问题、追根溯源，进行优化和调整以达到最优状态。

2 关键技术与方法

2.1 质量评定数据集构建

本节构建了基于模型定义的质量评定数据集，包括关键产品特性集、关键控制特性集、产品实测数据集三类数据集，如图2所示。其中，关键产品特性是一组与产品功能相关的特性，包括机械特性、几何特性、物理特性、化学特性等；关键控制特性是对关键产品特性起到重要影响作用的一组特性，包含工艺、制造等过程中的数据。关键产品特性中，几何特性是对产品质量影响最大的一项，反映了产品的几何状态。尺寸精度、位置精度、形状精度、表面粗糙度[12]等共同构成了产品的几何特性，对产品使用性能和可靠性寿命等有着重要影响，本文以几何特性作为主要研究对象。

产品实测数据集包含测量实例信息、测量坐标系、实测点数据等，表征了每一个产品的实际状态，通过分析产品实测数据集来反应该产品整体的质量好坏，进一步分析某一关键质量特性的波动，来分析其关联的关键控制特性，提前对可能出现的质量问题进行预判。

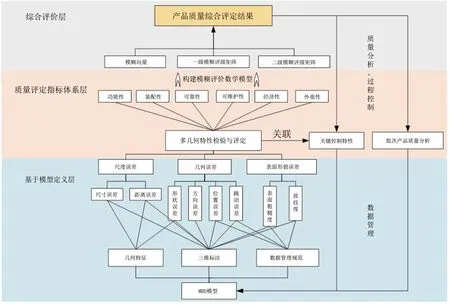
图1 基于多几何特性的质量综合评定总体框架

图2 质量评定数据集构成

2.2 几何要素拟合

构建典型几何要素的参数模型，包括直线度、平面度、圆柱度、圆度等，采用最小二乘法使偏移误差的平方和达到最小，其核心是基于已有的数学知识，构建元素的偏移误差，通过实现理论模型与测量值误差最小来求解问题[13]。其中，偏移误差包括代数偏移误差和几何偏移误差，其中代数偏移误差是点到代数方程的偏差；几何误差是指点到理论几何形状的法向距离偏差。

本文采用RANSAC算法（随机采样一致）来进行几何要素的拟合，相对于最小二乘拟合，RANSAC算法是一种用于数据处理的常用算法，能够在大量干扰数据存在的情况下，提取出需要的信息，在模型确定以及最大迭代次数允许的情况下，找到问题的最优解，相比较于最小二乘法，RANSAC适用于更多种测量方法获取到的实测点云数据，能够应用于更多的测量场景。其中，点云分割是提取出拟合所需点的过程，是几何要素拟合的重要环节，通过提取出点云中的不同物体，从而实现分而治之，突出重点。本文将该算法应用于实测点云的几何特征拟合中，结合本节构建的几何要素参数模型，求解各个参数。

2.3 基于模糊理论的质量评定方法

本文采用模糊综合评定法作为产品质量综合评定的方法，该方法通过将影响评定目标的所有因素进行综合考虑而得到评定结果。模糊综合评定法主要步骤包括：

1）评定目的。评定任务最终所要得到的结果。产品质量综合评定的评定目的是求解产品质量综合的、定量的描述。

2）评定指标体系。确定评定目的之后，构建评定指标体系。由影响评定目的的各项指标所构成，本文将评定因素分为一级评定指标层和二级评定指标层。

3）权重系数。权重系数表达了每一项评定因素对于评定目的的重要程度，可以基于一级指标层对其影响程度进行分析，从而计算权重值。4）评语集。评语集用于描述每一项评定要素及产品综合质量的评定等级，本文采用的评语集为：

5）评定模型。是评定目的、评定指标体系和评语集的集合。

评定框架如图3所示。

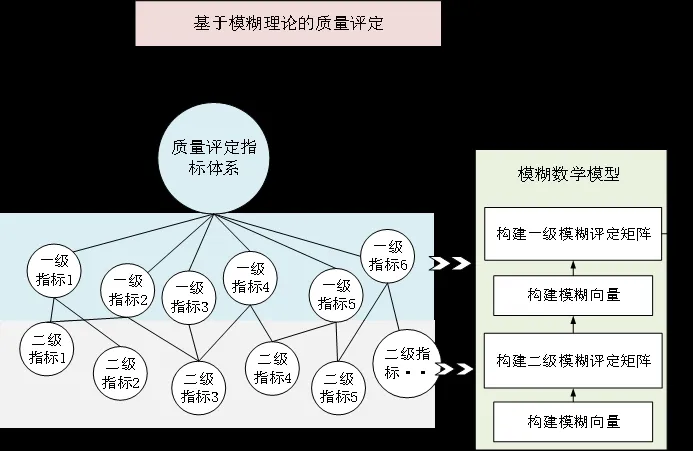
图3 基于模糊理论的质量评定框架

2.3.1 设计评定指标

将评定指标体系划分为三个层次：目标层、一级指标层、二级指标层：目标层为评定目的，即产品综合质量；一级指标的确定参考了《JB/T 8627-2006，机械工业产品质量特性重要度分级导则》中的产品质量特性分级内容，提炼出6类要求作为一级评定指标，包括：功能性要求、装配质量要求、可靠性要求、可维护性要求、经济性要求、外观性要求，具体内容如表1所示。

二级评定指标是一级评定指标的具体实现方式，本文二级评定指标为多几何特性，包括尺度误差、几何误差、表面形貌误差三类，一项或多项二级指标的表现情况决定了一级指标，存在着一对一或多对一的耦合关系，建立多级评定指标如图4所示。

图4 多级评定指标

表1 一级评定指标

通过对评定指标赋予权重值来保证评定结果的准确性与有效性。设一级评定指标集V={v1，v2，v3，v4，v5，v6}，对应的一级评定指标权重集A={a1，a2，a3，a4，a5，a6}，其中ai为vi的权重系数。对应于v1，v2，v3，v4，v5，v6的二级评定指标集为V1={v11，v12，…v1n}、V2={v21，v22，…v2m}…，其中v1i为一级评定指标v1的第i个二级评定指标，对应于二级评定指标集的权重系数为：A1={a11，a12，a13，…}、A2={a21，a22，a23，…}…

需要对各项二级评定指标进行权重分配，根据该指标相对于每一项一级评定指标进行权重分配，如表2所示为评定指标权重值设计表。基于实际生产过程、生产经验、市场需求等因素确定权重值。

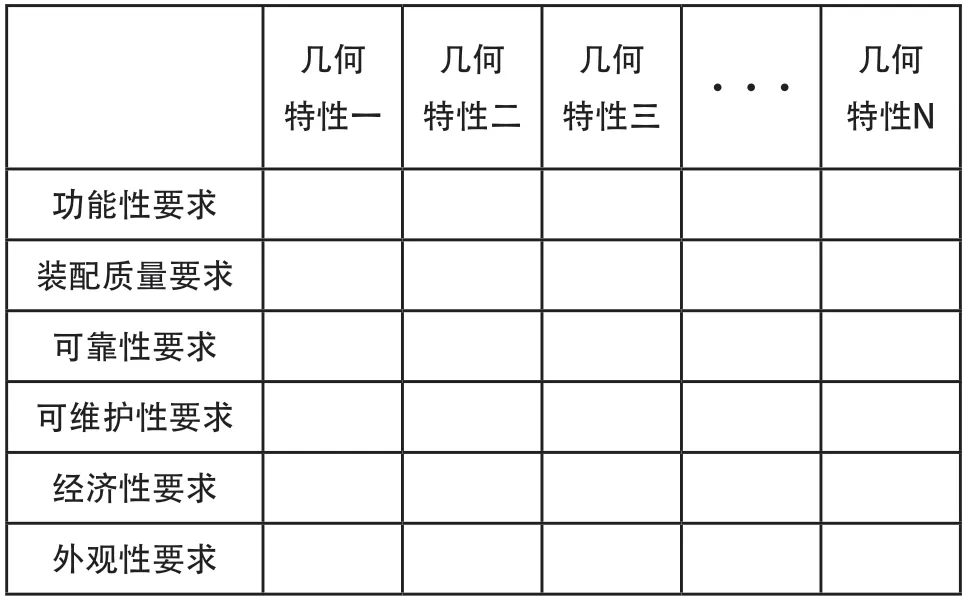
表2 评定指标权重值设计表

2.3.2 构建评定数学模型

模糊评定向量、模糊评定矩阵构成了模糊评定数学模型，其中，对应于一级评定指标和二级评定指标分别为一级评定矩阵和二级评定矩阵，通过求解一级模糊评定向量，基于最大隶属度原理求解产品质量的综合评定结果。

1）构建模糊向量

模糊向量（rij2，rij3，rij4）是对Vi中的第j个二级指标的评定向量，rijk是该指标关于评语集U中uk的隶属度，其中，本文设定评语集U为：

针对每一项二级评定指标进行打分X，按照模糊映射关系得出各因素的评定矩阵。设计模糊映射关系如下：

2）进行二级评定

Ri表示第i个一级指标vi对应的二级模糊评定矩阵。每个二级评定指标有着相对应的一个模糊向量，具体内容如式(5)所示：

[rj1，rj2，…rjm]表示第j个二级评定指标的模糊向量；

n该一级评定指标对应有n个二级评定指标；

m表示评语集因子的个数，本文设定评语集因子个数为4。

得到权重集Ai和二级模糊评定矩阵Ri后，便可进行模糊算子合成。以第一个一级指标为例，计算模糊算子。

3）进行一级评定

通过权重设计，可以获得一级指标的权重集A={a1，a2，a3，a4，a5，a6}，其中ai为vi的权重系数。设一级模糊评定矩阵为B，则：

其中，Bi对应第i个一级评定指标vi的评定结果向量，则：

其中，R为一级模糊评定矩阵，对R进行归一化处理后的R'，用于描述产品综合质量对于评语集中每一项因子的隶属度，r1对应“优”，r2对应“良”，r3对应“合格”，r4对应“不合格”，根据最大隶属度原则可知，P的数值对应评定集中的因子则是最终评定结果。

P数值越高，则对该评语的隶属度越高。在整个综合评定过程中，权重集的确定收到人为因素的影响，具有一定的主观性，需要根据实际情况和专业经验，根据零件功能和具体要求来确定权重集，对齐进行一致性检验，最终获得可靠正确的评定结果。

2.4 单件与批次产品质量评定

针对单件产品的质量评定和批次产品的质量分析问题，提出产品质量综合评定的四个维度，如图5所示。

图5 产品质量多维度评定

维度一：几何特性的合格性评定。将测量不确定度考虑在测量结果中，以分数的形式描述几何特性满足要求的程度，以60分作为合格分界线，低于60分为不合格，分数越高说明该几何特性质量越好。

维度二：产品质量综合评定。得到产品的多项几何特性质量评定得分之后，运用2.3.2节中提到的基于模糊理论的质量评定方法，计算产品整体的质量评定结果，该结果也是量化的分数形式，是一个综合了几何特性重要程度、实际测量结果和测量不确定度的评定结果。

维度三：批次产品某一几何特性合格性分析。针对批次产品的某一几何特性的质量评定分数进行分析，利用预控图等质量工具对该几何特性的质量波动情况进行查看，实现质量问题的及时发现和问题溯源。

维度四：批次产品的质量综合评定结果分析。针对批次性产品，每一个产品的质量综合评定结果的波动性进行分析。由于设计改变、生产加工工艺的变化等因素，产品质量也具有波动性，通过对批次产品质量波动情况的分析，可以判断生产过程是否受控，预测可能出现的质量问题。

综上所示，维度一和维度二是面向单件产品，侧重点是质量评定；维度三和维度四是面向批次产品，侧重点是在质量评定的基础上，对批次产品质量进行分析，发现其中的质量问题，实现质量控制。

3 应用验证

基于多几何特性的产品质量综合评定系统的设计思路是模型几何信息及非几何信息管理功能基于CAA应用框架对CATIA进行二次开发，数据处理及界面设计基于MFC（Microsoft Foundation Classes）应用程序框架完成。软件的技术体系架构自下而上可以分为数据层、应用层和表现层。数据层提供各类数据来源，包括产品管理信息、关键产品特性数据、关键过程控制数据、几何信息等；应用层实现系统的相关业务逻辑；表现层主要用于显示评定结果及各类数据的分层管理，如图6所示。

1）数据层：数据层包含了产品的管理信息（零件号、实例号等）、关键几何特性数据、关键控制特性数据、以几何特征表达的几何信息等，是整个质量评定系统的数据源；

2）应用层：应用层主要是实现系统的相关业务逻辑，包括功能界面实现层、算法服务层和相关的软件开发平台。其中，基于CAA应用框架实现基于模型的数据管理及可视化，包括CATIA工作空间创建、对话框设计、工具条封装、创建特征原型等[14]；基于MFC的应用程序框架发挥了MFC技术中创建对话框的便捷性，同时便于集成PCL的相关算法，包括基于随机采样一致算法的几何特征几何、几何误差评定、评定结果可信度分析等。在CATIA软件内部可以直接调用MFC界面实现相关的算法实现，同时两个平台基于中间文件可以实现数据的双向传递。

3）表现层：表现层基于CATIA环境，以结构规范树的形式对产品数据进行分层管理，可以方便的查询及导出数据，以及结合CATIA强大的建模能力，将实测数据关联到模型中，实现测量数据的可视化，以及在软件界面中查看各项评定要素。

本文选取柴油发动机关键件—连杆作为产品质量评定的实例分析对象。连杆是活塞与曲轴连接部件，是影响柴油发动机质量的关键部件之一，连杆的质量情况直接决定了发动机的性能、寿命、可靠性等，如图7所示为连杆三维模型。

图6 原型系统技术体系架构图

图7 连杆三维模型

连杆的质量检测内容为多类几何特性检测，包括几何误差、尺寸误差、表面形貌误差。确保几何特性满足质量要求是连杆质量保证的重要内容。通过构建质量评定数据集，确定需要检验的几何特性及关键控制特性，并基于MBD模型实现以上信息的统一建模，同时建立几何特性与控制特性的关联关系，为实现质量问题的追根溯源奠定基础。基于质量评定数据集构建出综合评定数学模型，可定量求解连杆质量综合评定结果。

在实现了单个连杆综合质量评定的基础上，从两个维度上对批次连杆质量进行分析：

1）针对批次连杆中某几何特性的质量波动情况，基于该波动情况映射到相应的加工工艺参数，实现质量控制的闭环过程；

2）针对每一个连杆的质量综合评定结果，构建其波动图，用于直观展示连杆质量是否稳定，以及可能出现问题的趋势。

3.1 产品质量评定数据集构建

将产品数据定义在MBD模型中，实现同一数据管理。如图8所示为几何特性信息的定义过程，通过选取需要定义的三维标注，将相关信息集成在结构规范数中，以便后续质量评定过程提取相应的信息。

图8 几何特性定义信息

3.2 几何要素拟合与误差评定

利用导入模型的实测点数据，利用随机采样一致方法进行几何元素拟合，进而求解几何误差值。从而对几何特性进行合格性的判定。

图9 几何特性数据集与质量评定界面

如图9所示软件界面为几何特性数据集集成在结构规范树与质量评定功能模块，通过选取需要评定的几何特性，计算质量评定得分，并显示在软件界面中，最终基于各项几何特性的评定得分，求得产品质量的综合评定结果。

图10 基于几何特性质量波动追溯控制特性问题

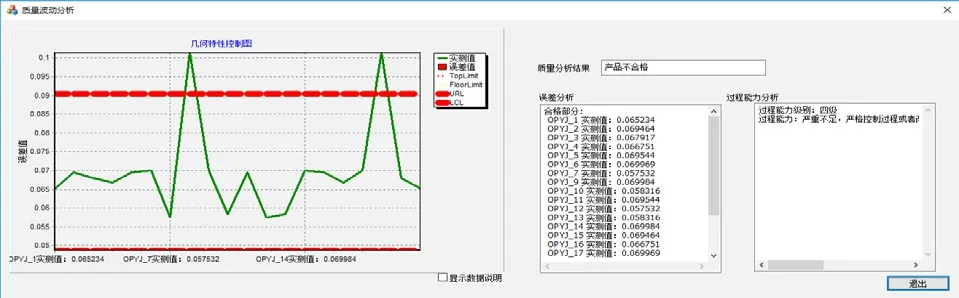
图11 产品质量综合评定得分波动图

如图10所示，针对某一项几何特性出现问题时，可将与其关联的加工工艺参数进行提取，帮助质量分析人员追溯质量问题源头。如图11所示，将该产品的多个实例的质量评定结果绘制成波动图，可以直观反映产品波动情况，及时发现可能出现的质量问题，实现质量控制和问题预警。

4 结语

本文从质量评定数据集构建、基于模糊理论的质量评定、基于三维模型的数据管理、几何误差拟合及评定等进行了研究，提出了基于多几何特性的质量综合评定总体框架，研究了基于模型定义的质量评定数据集，基于CAA二次开发技术和MFC应用程序框架实现了产品质量综合评定系统的设计与开发，并给出了具体的应用场景及原型系统应用示例。