基于滑模控制方法的光伏系统MPPT策略

王仁明，胡梦帆，张赟宁

(三峡大学电气与新能源学院，湖北宜昌 443000)

光伏系统利用光伏电池的光生伏特效应将太阳辐射能转化为电能，因其输出特性受外界环境的影响较大，使得其光电能转换效率较低。在环境温度和光照强度变化时，为了维持光伏电池的最大输出功率，最大功率点跟踪(MPPT)技术成为了光伏系统研究不可或缺的内容。

MPPT 控制是使光伏发电系统在复杂的工作环境中获得较好的性能的主要手段。MPPT 通过控制Boost 电路的占空比来使系统的工作点稳定在MPP 处。本文分析了孤立光伏电池(PV)系统的MPPT 控制问题，该系统结构如图1 所示，其主要组件有：PVG(将太阳能转换成电能)、Boost 电路(将PVG产生的电压提升为负荷需要的电压)和MPPT 控制器。

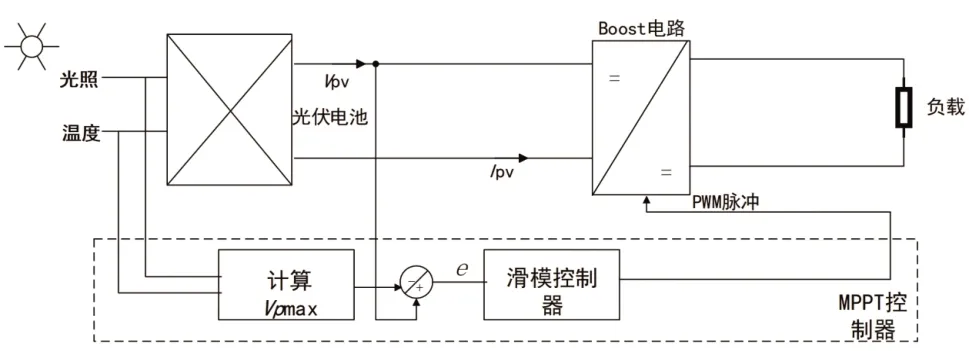
图1 光伏发电MPPT控制系统原理图

常用的MPPT 控制算法有恒电压法[1]、扰动观察法[2]、电导增量法[3]、改进型电导增量法[4]和模糊逻辑控制方法[5]等。这些算法虽然结构简单，在标准工况下控制精度高，但当天气条件快速变化时，跟踪速度和跟踪可靠性之间存在缺陷。由于滑模控制(SMC)对非线性系统具有较好的鲁棒性和较快的收敛速度，也被用于光伏系统的MPPT[6-8]，以便克服传统MPPT 控制算法的不足。文献[6]提出的滑模控制方法将幂次趋近律和等效控制结合，改善了系统的动态性能。文献[7]提出的神经网络-滑模算法利用神经网络逼近控制器的不确定部分，有效消去了非线性不确定因素对控制系统的影响。文献[8]提出的SMC 策略达到了预期控制效果，结果优于扰动观察法等传统方法。基于此，本文提出了一种用于光伏系统MPPT 的滑模控制方法，该方法适用于在光照强度和电池温度变化时调节系统的最大输出功率。首先，对系统的最大功率点处电压值进行估计，然后将实际输出电压值与计算得到电压估计值之间的差值作为滑模控制器的输入信号，通过滑模控制器的输出来调节占空比，以实现最大功率点跟踪。

1 光伏发电系统

1.1 光伏电池数学模型

在光伏电池模型里，光伏电池的输出电流I与输出电压V之间的数学关系式[9]为：

式中：Iph是光生电流；I0是饱和电流；n为理想因子，1＜n＜5；k是玻尔兹曼常数，其值为1.38×10－23J/K；q是电子电荷量，其值为1.6×10－19C；θ 是电池温度。

式(1)可表示为：

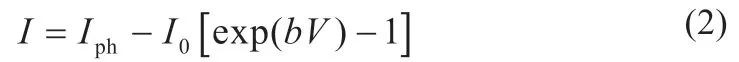
式中：b=q/(nkθ)。

当光伏电池处于短路时，短路电流Isc=Iph。当光伏电池处于开路时，式(2)简化为：

式中：Voc是光伏电池的开路电压。

当光伏电池在最大功率点时，I=Im，V=Vm，由式(2)可得：

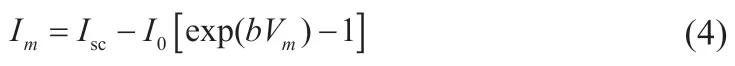
式中：Im是最大功率点处电流值；Vm是最大功率点处电压值。因此，光伏电池的数学模型为：

其中，参数Isc、Voc、Im、Vm和b均为标准工况(S=1 000 W/m2，θ=25 ℃)下的值，均为常数。

1.2 Boost 变换器模型

DC-DC 升压电路用于连接光伏电池与负载，以便控制直流输出电压，同时，也可以调节光伏电池的最大功率点。Boost 电路如图2 所示。

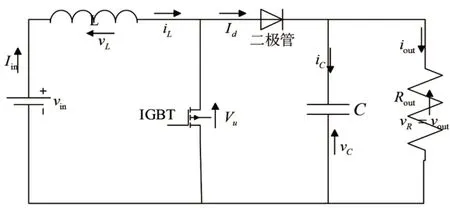
图2 Boost电路图

根据其IGBT 开关管的不同状态，Boost 变换器可包括两个阶段。

阶段一：当IGBT 合上，二极管断开，电感L从电源vin获得能量，负载R从电容C得到能量。此时，由基尔霍夫定律可得如下状态方程：

阶段二：IGBT 断开，二极管形成通路，电源vin和电感L一起对电路的其他元件充电。此时，电路动态方程为：

式(10)的静态解[10]可表示为：

式中：D表示占空比。

假设Boost 电路的所有原件均是理想元件，即它的转换效率为100%，则可以推出：

式中：Rpv为光伏电池的等效电阻。

2 MPPT 控制器

为了便于SMC 设计，需要首先估计出MPP 处的电压Vpmax，然后用光伏电池的实际输出电压Vpv与估计值Vpmax的差值e=Vpv－Vpmax作为SMC 控制器的输入，使之控制Boost 电路的占空比，从而控制MPP。

2.1 最大功率点电压Vpmax的估计

由于式(5)是在标准条件下的光伏电池数学模型，但光伏系统通常工作在可变的环境中，即Voc、Vm、Isc、Im和b均随S和θ的变化而变化。于是，用另一组与S和θ 有关的变量Voc'、Vm'、Isc'、Im'和b'分别替代Voc、Vm、Isc、Im和b，则式(5)修正为：

式中：Δθ=θ－θref；ΔS=S/Sref－1。

其中，θref=25 ℃，Sref=1 000 W/m2，α=0.002 5 ℃，β=0.5，γ=0.002 88/℃。S和θ 的值可以由光照传感器和温度传感器测量。

式(22)即为MPP 光伏电池的电压。它与电池的工作环境S和θ 有关。取参数值Voc=66 V，Vm=54.2 V，Isc=25.44 A，Im=23.25 A，代入式(22)可得Vpmax与环境参数S和θ 的关系如图3所示。

2.2 滑模控制器设计

在获得了Vpmax之后，便可以利用Vpmax来设计滑模控制器。取滑模面为s=e=Vpv－Vpmax，令控制律为

图3 Vpmax与环境参数S和θ 的关系图

为了证明系统符合滑动模态的可达性条件，取Lyapunov函数为，所以，当s＞0，即开关闭合时，意味着占空比将增加。由式(12)可知，Rpv将会下降，通过分析如图4 所示的光伏系统动态I-V特性曲线可知，光伏电池的输出电流I将会增加，从而由式(1)可知光伏电池的输出电压将减小；于是可以推出当输出电压增大/减小时，相对应的输出电流I减小/增大。因此在s＞0 时，有和同理，当s＜0，即开关打开时，意味着占空比将减小，Rpv将会增加；由光伏系统的动态I-V特性图可知，光伏电池的输出电流I将会减小，相反光伏电池的输出电压Vpv将会增加。假如负载Rout变大，则电压Vpv增加以及电流I减少，得到

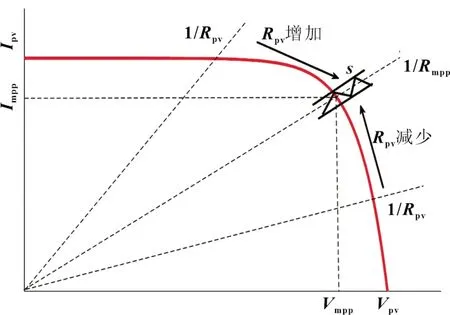
图4 I-V特性曲线和MPPT跟踪过程

由Lyapunov 稳定性理论得到s可以达到s=0 以上，这意味着系统可以到达期望的最大功率点处的电压值。

3 仿真结果分析与讨论

本文采用Matlab/Simulink 平台搭建系统的仿真模型，如图5 所示。仿真参数设置如下：Voc=66 V，Vm=54.2 V，Isc=25.44 A，Im=23.25 A；电容C1和C2的电容值均为2 mF，电感为0.01 H，纯电阻负载R=500 Ω。

图5 基于Simulink的光伏系统仿真模型

为了研究本文提出的基于最大功率点电压计算与滑模控制的算法的效果，将采用对比组，对两种方法在温度不变、光照强度改变，光照强度不变、温度改变以及在温度不变、光照强度改变且负载变化这三种情况下进行跟踪仿真。

3.1 温度不变而光照强度改变

假设θ=25 ℃不变，光照强度S在0 s 时是400 W/m2，0.3 s降为300 W/m2。图6 是利用本文的设计方法仿真的系统输出功率随光照强度S改变时的变化情况。由图6 可知，在仿真试验的初始阶段，光照强度为400 W/m2，光伏系统在0.03 s 左右跟踪到了最大功率点，其光伏系统的输出功率维持在445.2 W 左右，且达到稳态时系统处于非振荡状态。

图6 基于滑模控制算法的系统输出功率

为了表明本文设计方法的优越性，在同样条件下，基于传统的扰动观察法的仿真曲线如图7 所示，其输出功率变化曲线在0.04 s 达到最大功率点，存在明显的振荡。在0.3 s 时，光照强度由400 W/m2下降到300 W/m2，基于滑模控制的光伏系统约在0.01 s 后再次处于稳态，该系统的输出功率变化曲线较平稳；而传统的扰动观察法在约为0.02 s 后再次处于稳态，且输出功率曲线波动较大。基于滑模控制方法的光伏系统平均跟踪时长分别约是0.02 s，而基于传统的扰动观察法的光伏系统平均跟踪时长约为0.03 s；从功率曲线的平稳程度看，基于滑模控制方法的光伏系统也优于基于传统的扰动观察法的光伏系统。

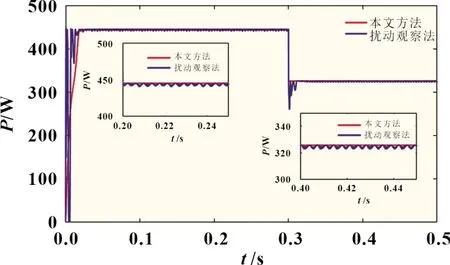
图7 两种方法在温度不变光照强度改变时的输出功率

3.2 光照强度不变而温度逐渐上升

考虑到实际环境中光伏电池的温度在光照强度不变时都存在一个缓慢上升的过程，假设S=1 000 W/m2恒定，温度θ在0 s 时是－5 ℃，0.1～0.4 s 缓慢上升到45 ℃，温度的变化如图8 所示。

图9 是利用本文的设计方法仿真的系统输出功率随温度θ 改变时的变化情况。由图9 可知，在起始温度为－5 ℃的条件下，系统跟踪到最大功率值并达到稳态的时间约为0.03 s，稳态时，系统功率曲线的平稳程度较好。

图8 光照强度不变时的温度上升情况

图9 基于滑模控制算法的系统输出功率

在同样条件下，基于传统的扰动观察法的仿真曲线如图10 所示，其输出功率曲线在0.05 s 达到最大功率点并存在明显的振荡。在0.1～0.4 s，光伏电池的温度缓慢上升，在此过程中，基于滑模控制方法的功率曲线的平稳程度较好，而传统的扰动观察法输出功率曲线波动明显。基于滑模控制方法的光伏系统跟踪速度快于传统的扰动观察法，从功率曲线的平稳程度看，基于滑模控制方法的光伏系统功率曲线振荡不明显，而基于传统的扰动观察法的功率曲线有明显的振荡。

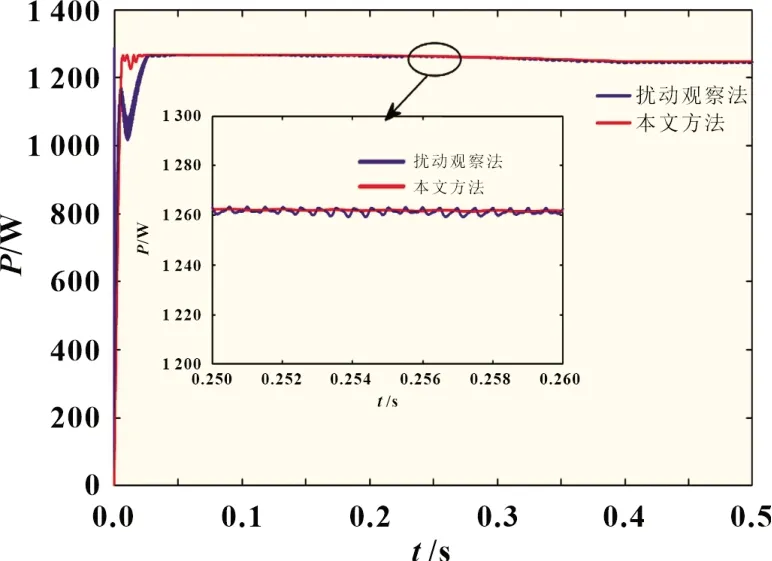
图10 两种方法在光照强度不变而温度改变时的输出功率

3.3 温度不变而光照强度改变且负载改变

当θ=25 ℃不变，光照强度S在0 s 时是400 W/m2，0.3 s 时降为300 W/m2，负载在0.4 s 时从500 Ω 增加到700 Ω 时，两种方法的仿真曲线如图11 所示，在光伏电池的光照强度为400 W/m2时，基于滑模控制算法的系统跟踪到最大功率值并达到稳态的时间是传统扰动观察法的一半，为0.03 s；在光伏电池的外界光照强度减弱至300 W/m2时，基于滑模控制的光伏系统约在0.01 s 后再次处于稳态，而传统的扰动观察法在约为0.03 s 后再次处于稳态；在负载突然增加至700 Ω 时，本文的方法没有出现任何功率曲线突变，而扰动观察法在负载变化时功率曲线有波动，恢复到之前的稳态所需的时间是0.03 s左右。所以本文方法抗外界扰动的能力较强。

图11 两种方法在温度不变光照和负载改变下的输出功率

4 结论

本文研究了光伏发电系统如何有效地通过Boost 变换器供电于负载的问题。为了改善系统的供电效率和性能，提出了基于滑模控制方法对最大功率点进行跟踪与升压DC-DC变换电路相结合的综合策略。首先计算在任意光照条件和电池温度环境下的光伏系统的最大功率点电压估计值，然后将实际输出电压与计算得到电压估计值的差值作为滑模控制器的输入信号来实现MPPT。仿真结果显示该方法比传统的扰动观察法具有追踪速度快、稳态精度高、抗扰动能力强等优点。