陶瓷基复合材料基体唇形裂纹失效规律研究

2021-04-30 01:42李湘萍王小峰

计算力学学报 2021年2期

李湘萍，陈希，张鸿，王小峰

(中国民航大学中欧航空工程师学院，天津 300300)

1 引言

陶瓷基复合材料具有重量轻、强度高以及耐高温、耐腐蚀等优点，是航空发动机和火箭发动机热端部件的理想材料。在陶瓷基复合材料的制备过程中，基体内部会生成一些缺陷，如裂纹、孔洞和位错等[1]；在受载状态下，基体开裂也是陶瓷基复合材料最早出现的一种损伤形式。由于陶瓷基复合材料基体为脆性材料，对缺陷或裂纹十分敏感，故其失效机理和失效过程变得更为复杂。

由于基体裂纹的存在，陶瓷基复合材料在使用过程中很容易发生性能退化和失效[2]。建立基体裂纹失效准则是建立陶瓷基复合材料失效模型的基础，也是研究其细观损伤演化的前提，很多学者对此开展了研究。脆性基体材料在应力集中处的裂纹萌生是复合材料失效开始的重要判据之一，Henningera等[3]采用内聚力区模型准则预测脆性基体材料中V型裂纹的不稳定扩展；之后为考虑更为复杂的环境条件，Deng等[4]基于能量失效准则，得到了高温环境下非稳态第一基体开裂应力(FMCS)；Farrokhabadi等[5]则采用摩尔-库伦准则作为基体初始裂纹的判据，从局部失效出发，进一步研究层合板渐进损伤问题。同时，不少学者探究了基体裂纹扩展、裂纹偏转、裂纹穿透与界面脱粘之间的失效准则问题，如Pompidou[6]基于Cook等[7]的研究结果，分析了陶瓷基复合材料内椭圆形裂纹尖端的应力分布，建立了基体裂纹偏转的应力失效判据；Parmigiani等[8]以临界位移为失效标准，结合了强度和韧性参数的内聚力区准则研究了脆性基体材料的基体裂纹在界面处的偏转判据；更加全面地考虑多种失效机制，Martin等[9,10]通过建立能量释放率准则研究了基体裂纹向界面扩展、界面脱粘、裂纹偏转以及裂纹穿过纤维多种失效机制的发生判据；Yan[11]基于正向周应力准则研究了颗粒增强陶瓷基复合材料的裂纹偏转准则。针对陶瓷基复合材料失效行为的预测，Dassios[12]基于裂纹尖端应力强度因子研究了陶瓷基复合材料的力学行为；Tracy等[13,14]使用J积分和来自数字图像相关(DIC)的全场变形数据来表征连续纤维陶瓷基复合材料韧性；Gao等[15]以基体应变能准则作为基体损伤准则，分析了加载和卸载过程中纤维滑移区分布，进一步得到了单向纤维增强陶瓷基复合材料的本构关系；Becher等[16]建立了威布尔随机失效准则来预测CMCs的失效过程；与文献[16]以基体应变为失效参数标准不同，Higuchi等[17]则基于强度参数，建立威布尔统计强度模型，建立了CMCs失效准则，用于模拟3D编织陶瓷基复合材料失效过程；Zhang等[18]建立了应力强度模型预测基体开裂过程来预测SiC/SiC复合材料的拉伸失效行为，结果表明该模型优于以临界基体应变能准则建立的模型和以概率统计方法建立的模型；Li[19,20]以基体临界应变能准则作为基体多裂纹扩展判据，研究了纤维泊松收缩对CMCs基体多裂纹扩展演化的影响，该准则也适用于高温环境中对基体多裂纹开裂的裂纹密度预测；Skinner等[21]以能量释放率为基础，通过应力强度因子与能量释放率之间的关系，得到了基体裂纹尖端应力强度因子准则，进一步研究了CMCs的损伤演化行为。

以上准则的建立都是针对直线型、三角形或者椭圆形这类规则形裂纹，实际陶瓷基复合材料的基体裂纹要复杂得多。试验表明[22],陶瓷基复合材料的基体内部存在着中间大两头小的曲边多角形裂纹。很多学者采用唇形裂纹模型来表征这种带尖角的裂纹[23]。此外，不同于脆性材料，陶瓷基复合材料的基体由于纤维的增韧，表现出一种准脆性的特性,其力学行为具有明显的非线性[24]，这种特性是与裂纹尖端的应力场和位移场密切相关的[25]。本文建立唇形裂纹数学模型，采用复变函数的方法，通过保角映射得到在横向拉伸载荷下唇形裂纹尖端应力场和位移场的解析解；在此基础上分别推导了唇形裂纹的应力强度因子准则和最大能量释放率准则，结合算例分析陶瓷基复合材料唇形裂纹的几何参数、外载荷以及纤维分布对失效准则的影响规律。

2 唇形裂纹应力场和位移场求解

2.1 建立基体唇形裂纹模型

假设陶瓷基复合材料基体内存在任一唇形裂纹，将陶瓷基复合材料基体看作无限大平面，a为唇形裂纹半长，h为唇形裂纹半宽，唇形裂纹关于x和y轴对称分布，β=h/a为唇形裂纹的半宽与半长的比值，如图1所示，本文认为β相同的唇形裂纹具有相同的几何特征，半长a和半宽h则表示

图1 受到横向载荷的唇形裂纹模型

唇形裂纹具有不同的尺寸。假设陶瓷基复合材料受到横向拉伸载荷的作用，唇形裂纹位于面内并且裂纹边界是自由边界，受到无穷远处沿y轴的均布拉应力σ∞作用。

(1)

在横向拉伸载荷下，在图1所示平面内应力σy(x,y)和位移Xy(x,y)的表达式为

(2)

(3)

式中μ=E/2(1+ν),κ=(3-ν)/(1+ν)，E为陶瓷基体的弹性模量，ν为泊松比。

假设唇形裂纹边界用L表示，且在边界L上不受力，即边界L上的面力Tx=Ty=0，唇形裂纹边界的应力边界条件表示为

(4)

2.2 复势函数求解

(5)

该保角映射将z=x+iy裂纹平面上的唇形裂纹内部映射成了ζ=ξ+iη平面上的单位圆内部，唇形裂纹的边界映射为单位圆的边界。并且有w(i)=-a,w(-i)=a,w(1)=hi,w(-1)=-hi。

在受到无穷远处拉应力σ∞的作用下，自由界面唇形裂纹的复势函数φ(ζ)和Ψ(ζ)通式可表示为

(6)

取单位圆周上的任一点p，则有p=ei θ，θ为该点幅值。将保角映射Z=w(ζ)代入式(4)，并对其取共轭，得到单位圆周上任意点的应力边界条件为

(7)

(8)

(9)

(10)

为了便于计算，记

(11)

式中

F(ζ)=-J1-J2

(12)

式中J1和J2分别为积分函数的主值，具体表达式为

同样的方法可以得到J(ζ)的解析解，可表示为

(13)

(14)

同理，也可以得到式(10)的解析解,

(15)

将式(14,15)代入式(6)可得两个复势函数的解析解，

(16)

(17)

2.3 唇形裂纹尖端应力场和位移场求解

根据保角映射，式(2)应力场σ(x,y)的表达式可以改写为

(18)

同理，位移场X(x,y)的表达式也可写为

(19)

将式(5，16，17)代入式(18，19)，可得应力场和位移场关于单位圆平面上映射点的解析解。采用逆映射，即可得到在(x,y)平面内的应力场和位移场σ(x,y)和X(x,y)。

图3分别给出在横向载荷σ∞=100 MPa 下，三种不同形状(β不同)或者不同尺寸(β相同)裂纹尖端应力场和位移场的理论计算与有限元数值模拟的结果对比，其中基体的弹性模量Em=300 GPa，泊松比ν=0.25。有限元计算采用Abaqus中的扩展有限元法实现，有限元模型及其网格划分结果如图2所示，上下端面分别施加对称的均匀分布拉伸载荷σ∞=100 MPa。从图3可以看出，除了裂纹尖端的奇异性造成的有限元计算结果与理论计算结果相差较大以外，其他部分理论计算结果与有限元计算结果相差不大；此外，当唇形裂纹比较小时，有限元受网格的影响，其计算结果与理论结果有一定偏差。图3结果证明基于唇形裂纹模型计算得到的应力应变场是有效的。相较于有限元计算方法，本文通过参数化方法更快速地得到了唇形裂纹的横向拉伸应力应变场，避免了因为划分网格而造成的计算误差，既体现了唇形裂纹尖端的应力集中现象，又保持了唇形尖端的应力奇异性。

图2 唇形裂纹有限元模型

图3 有限元计算结果与本文计算结果对比(σ∞=100 MPa)

3 唇形基体裂纹失效准则

应力强度因子准则作为裂纹失效的判断依据是传统的断裂力学方法，是更多关注于裂纹尖端的一种局部准则。能量释放率准则更多地关注于裂纹开裂面，同时考虑了材料性能的作用效果。本文进一步推导出两种失效准则的表达式。

3.1 应力强度因子准则

裂纹左端点x=a处的应力强度因子定义[28]为

(20)

式中ζ1为裂纹尖端点，即点(a,0)。

将式(5,16)代入式(20)，可得唇形裂纹尖端的应力强度因子的表达式

(21)

受到无穷远处沿y轴均布拉应力σ∞作用的唇形裂纹仅存在I型裂纹扩展，此时，裂纹扩展方向为沿着唇形裂纹尖端的方向，并且当满足K>KI C，基体裂纹将会发生扩展。

3.2 最大能量释放率准则

对于脆性材料，通常是在得到裂纹尖端应力强度因子后，通过经验公式换算得到裂纹尖端能量释放率[29]，优点是不考虑裂纹尖端复杂的应力应变场，便于计算。但是陶瓷基复合材料由于纤维的增韧，基体表现出一种准脆性的特性，这种特性与裂纹尖端的应力应变场密切相关。因此为考虑复杂裂纹造成的裂纹尖端应力应变场变化，在图1所示y轴拉伸载荷作用下，假设裂纹的初始长度为a，扩展后的裂纹长度为a+Δa，在裂纹扩展的过程中，裂纹扩展段上面力消失的同时，产生了新的张开位移2Xy(x,y)，因此势能Π的变化为

(22)

由此，裂纹尖端最大能量释放率可表示为

(Δa-x,π)dx

(23)

为简化计算，将积分改写为黎曼和的形式，

(24)

由于图1仅存在I型裂纹扩展，当裂纹尖端的最大能量释放率满足G>GI C，基体裂纹将会沿着唇形裂纹尖端的方向失稳扩展。

4 算例分析

以连续纤维增强C/SiC陶瓷基复合材料为例，SiC基体的弹性模量Em=300 GPa，泊松比ν=0.25，C纤维的弹性模量Ef=200 GPa，泊松比ν=0.3，受到如图1所示横向载荷的作用。

4.1 几种模型的比较

图5分别给出了相同半长的唇形裂纹、Gri-ffith 裂纹和椭圆裂纹计算得到的裂纹尖端应力强度因子K和最大能量释放率G随裂纹半长a的变化结果，其中假设唇形裂纹和椭圆裂纹的宽长比β=0.5不变，Griffith裂纹的宽度趋于0，但是长度与唇形裂纹和椭圆裂纹的长度相同。可以看出，基于唇形裂纹计算得到的应力强度因子准则和最大能量释放率准则的预测规律与Griffith裂纹和椭圆裂纹的预测规律相同,即随着裂纹半长的增加，三种裂纹的应力强度因子和最大能量释放率都逐渐增加。在相同半长情况下，唇形裂纹计算得到的应力强度因子和最大能量释放率都是三种裂纹中最大的。这是因为唇形裂纹在计算裂纹尖端应力强度因子时，能够考虑裂纹复杂几何形貌的影响；在计算最大能量释放率时，还能够考虑裂纹尖端应力场和应变场的变化情况。因此，基于唇形裂纹的失效准则对裂纹尖端敏感性更高，又考虑到实际陶瓷基复合材料的基体裂纹多为中间大，两头小的曲边多角形，唇形裂纹更适合作为陶瓷基复合材料基体裂纹模型，对唇形裂纹失效准则规律的探究也是十分必要的。

图5 相同半长的唇形裂纹、Griffith裂纹和椭圆裂纹(β =0.5)

4.2 几何参数的影响

图6为基体内存在相同形状不同大小的唇形裂纹，即宽长比β为定值，半长a或半宽h变化。可以看出，随着唇形裂纹半长a的增加，半宽h也随之成比例增加，不同大小唇形裂纹尖端应力强度因子K呈1/2幂指数增加，最大能量释放率G呈线性增加。说明基体内存在相同形状的裂纹时，裂纹尺寸越大，依据应力强度因子准则，裂纹越容易起裂，而依据最大能量释放率准则，裂纹则越容易发生失稳扩展。

图6 相同形状不同大小的唇形裂纹

图7为基体内存在开口宽度相同长度不同的唇形裂纹。即半宽h为定值时，唇形裂纹在受载情况下沿着裂纹尖端的方向发生扩展，半长a不断增加的情况。可以看出，随着唇形裂纹半长a的增加，宽长比β不断降低，唇形裂纹尖端应力强度因子K呈非线性增加，最大能量释放率G呈线性增加。说明基体开裂后，基体裂纹更容易起裂和失稳扩展。

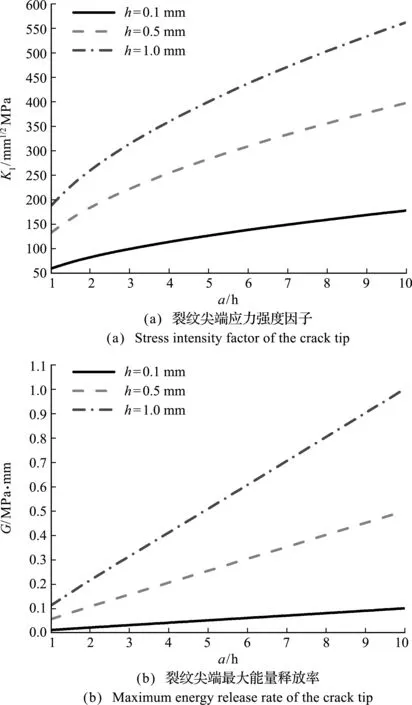
图7 开口宽度相同长度不同的唇形裂纹

图8为基体内存在裂纹长度相同开口宽度不同的唇形裂纹。即半长a为定值时，唇形裂纹在受载情况下产生了变形，半宽h发生变化的情况。可以看出，随着唇形裂纹半宽h的增加，宽长比β不断增加，裂纹尖端应力强度因子K和最大能量释放率G呈较为平缓的增加。说明当基体内存在相同长度的裂纹时，开口宽度越大，越容易起裂和失稳扩展。但是当宽长比β接近1时，即唇形半宽h逐渐等于唇形半长a时，裂纹尖端应力强度因子K和最大能量释放率G会随着半宽h的增加而略有下降，从图9可以看出，裂纹尖端应力强度因子K和最大能量释放率G在0.8≤β≤1时先增加后下降。根据于静等[30]的研究，当半宽h大于半长a，即宽长比β>1时，唇形半宽的增加会抑制裂纹的扩展。本文只研究唇形裂纹宽长比β<1的情况。在相同宽长比β情况下，基体裂纹越长，越容易起裂和失稳扩展。

相比于图6和图7，半宽h的影响程度要远小于半长a，即在横向拉伸载荷下，裂纹变形的影响要小于裂纹扩展的影响。

图8 长度相同开口宽度不同的唇形裂纹

图6～图8表明,对于不同几何参数的唇形裂纹，裂纹尖端应力强度因子K呈非线性变化，最大能量释放率G呈线性变化，即采用最大能量释放率准则的基体裂纹的扩展速率要大于采用应力强度因子准则的。

4.3 外载荷对最大能量释放率的影响

由式(22)，外载荷与裂纹尖端应力强度因子成正比关系；由式(23)，外载荷影响了唇形裂纹尖端的应力场和位移场分布，继而对最大能量释放率产生了更为复杂的影响。图10给出唇形裂纹尖端最大能量释放率随不同拉应力σ∞的变化曲线。可以看出，对于不同形状不同大小的唇形裂纹，随着外载荷的不断增加，裂纹尖端最大能量释放率呈抛物线增加，外载荷越大，增加的速率越快。相同外载荷条件下，基体裂纹越长，越容易失稳扩展；基体裂纹变形越大，越容易失稳扩展；基体裂纹尺寸越大，越容易失稳扩展。这也与图6～图8的结论一致，符合陶瓷基复合材料基体失效特征。