结合旋变误差补偿的轴角数字转换器研究
杜春洋,张小乐,罗 毅
联创汽车电子有限公司,上海 201206)
0 引 言
在电机驱动系统中,实时的电机转子角位置信息是一个关键的量,需要得到高精度的转子位置信息才能提高电机驱动控制的精确性和快速性。在众多位置传感器中,旋转变压器的抗干扰、抗振能力强,对环境的要求低,能够应用于环境恶劣的场合,因而得到了广泛应用。但是,轴角数字转换器(RDC)的性能制约着旋转变压器测角系统的精度和可靠性。专用RDC芯片虽然能实现高精度解码,但是其规格有限、价格昂贵、接口电路复杂[1-3]。
随着数字化的不断发展,面对传统RDC芯片存在的缺陷,为了能将旋转变压器输出的模拟信号更便捷地转换为数字信号,数字RDC应运而生。数字RDC摒弃了原有的专用芯片,通过AD采样将旋转变压器输出信号转化为数字信号,再利用单片机、DSP或FPGA等处理器对信号进行解码,进而得到准确位置信息[4-5]。
对于RDC系统的研究,一般是针对绝对理想的旋转变压器进行的。然而在实际应用中,由于多种因素影响,旋转变压器的输出往往包含多种误差的非理想信号[6-7]。其中,模拟电路和A/D转换器的零点偏移会引起零位误差,旋转变压器2个输出端的灵敏度或模拟处理电路中的两路放大倍数不同会引起幅值误差,旋转变压器两相输出绕组非完全正交会引起正交误差,同时气隙磁场的非正弦分布则会引起谐波误差[8]。为了消除这些误差,有必要对RDC数字补偿进行研究,以提高系统的测量精度。文献[9]采用改进加权最小二乘法实时计算误差参数并进行抑制,利用参数辨别与校正环节重构旋转变压器输出信号。文献[10]通过积分运算消除振幅不平衡和不完全正交误差,提高了计算角度的准确性。文献[11]采用自适应神经网络的误差校正方法,其非线性处理效果明显,计算精度高,但是迭代运算次数多,计算过程复杂,响应速度慢。上述文献均只考虑零位、幅值和正交误差,并未考虑谐波影响。文献[12]采用谐波抑制提高绝对磁编码器精度的方法,通过梯度下降法不断学习,其结果精度高,但迭代次数多,响应时间较长。本文针对旋转变压器输出信号中的零位误差、正交误差和幅值误差采用椭圆假设算法进行消除,并研究采用谐波分离法实现对信号中谐波误差进行补偿。通过仿真和试验进行了分析验证,证明了该方法的有效性。
1 旋转变压器测角组成及原理
旋转变压器从原理上看是一种可以旋转的变压器,一次侧和二次侧绕组分别在定子和转子上。一、二次侧绕组之间的电磁耦合程度与电机转子实时位置角有关。因此,输出电压也与转子角度有关。旋转变压器的结构及信号关系图如图1所示。旋转变压器工作时,在激励绕组上施加高频的正弦或余弦信号,通过特殊的转子结构,使得正交的正、余弦两相绕组输出包含转子位置信息的调制信号。
设激励电压为ve=uecosωet,当转子转过一定角度θ后,旋转变压器两相绕组上输出的调制信号分别为
(1)
式中:k为旋转变压器的变比;ue为激励信号的幅值;θ为旋转变压器转子的位置信息;ωe为激励信号的角频率。

图1 旋转变压器的结构及信号关系图
角度测量系统中,旋转变压器两相输出调制信号被输入到DSP的A/D转换单元,当cosωet=1时,对传感器的两路输出信号进行同步采样可得:
(2)
为了得到高精度的转子位置角信息,采用了三相同步参考坐标系锁相环(SRF-PLL),其具体结构框图如图2所示。
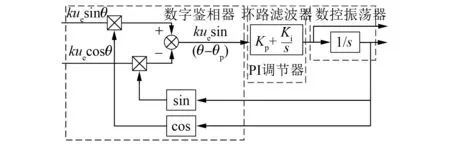
图2 SRF-PLL原理图
将采样得到的旋转变压器正、余弦输出信号用一个矢量v表示:
(3)
图2中的鉴相器是通过同步旋转坐标系(SRF)变换来实现的。SRF如图3所示,由一个两相静止坐标系αβ和一个以角速度ωp逆时针旋转的坐标系dq组成,dq坐标系与α轴的夹角为θp。
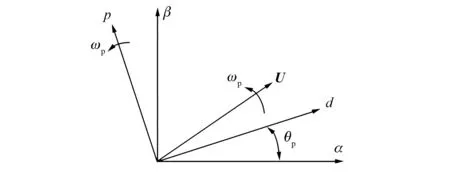
图3 SRF
矢量v在SRF下进行变换得到:
(4)
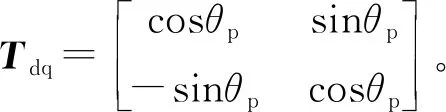
令:uerr=uq=kuesin(θ-θp),uerr表示跟踪误差,当sin(θ-θp)≈θ-θp,即角度误差较小时,则有:
uerr=kuesin(θ-θp)≈kue(θ-θp)
(5)
经过反馈闭环,跟踪误差uerr最终趋近于零,可以近似认为角度误差θ-θp趋近于零,通过积分和角度翻转即可得到旋转变压器转子位置角估计信号。
根据上述分析,当跟踪误差较小时,可以得到系统的闭环传递函数为
(6)
式中:Kp、Ki分别为PI调节器的比例系数和积分系数。
从SRF-PLL解码算法的闭环传递函数可知该算法具有低通滤波特性,因此可以滤除旋转变压器两相输出信号中的高频抖动分量,得到高精度的转子位置信息。
2 旋转变压器误差分析与补偿
在实际应用中,受旋转变压器的自身缺陷、安装问题以及RDC系统外围电路的影响,其输出的两相调制信号中一般会存在各种误差分量,表现为两相输出信号幅值不平衡、两相输出信号相位非完全正交、包含直流分量等。此外,旋转变压器的传感器易受到磁场的影响,比如,旋转变压器磁场非完全正弦化、定子磁场干扰(电枢反应)和气隙磁场随温度而变化的干扰等。这种情况下,旋转变压器输出信号会包含各次谐波,会发生畸变,进而影响转子角度估算精度。
2.1 基于椭圆假设算法的误差补偿
理想情况下,旋转变压器输出信号是一组理想正交信号,分解到横轴为正弦,纵轴为余弦的平面上,轨迹为一个完美的圆。当存在幅值不平衡、相位非正交、直流分量误差时,轨迹将会变成一个椭圆,此时研究采用基于最小二乘法的椭圆假设算法进行补偿。设理想旋转变压器输出信号分别为Ss和Sc,合成矢量轨迹圆的半径为H0,圆周方程为
(7)
考虑上述3种误差后得出两相信号表达式:
(8)
式中:Ks、Kc表示正余弦信号增益系数;φp为非正交偏差角;b1、b2为正余弦信号的直流偏置。
结合式(7)和式(8)可得包含误差信号的椭圆方程:
(9)
假设由A/D采样得到m个样本数据点(Ss1i,Sc1i),其中i=1,2,…,m。拟合曲线选取椭圆一般式作为拟合函数,则椭圆的一般方程展开式为
(10)
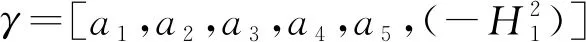
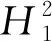
(11)
因为旋转变压器所采集的数据点不可避免地会散落在实际椭圆的边界周围,难以保证每个采样点均恰好落在实际椭圆曲线上,所以f(γ,S1i)在采样点(Ss1i,Sc1i)处的取值并不为零,而是带有一定程度的误差含量。为了改善采样数据的拟合偏差,可以将采样点(Ss1i,Sc1i)到拟合曲线f(γ,S1i)间的代数距离最小化,以达到最优的拟合效果。由最小二乘法原理可知,曲线拟合误差最小时,两者代数距离的平方和最小,即求解以下目标函数的最小值:
(12)
根据多元函数的极值原理,要使函数f(a1,a2,a3,a4,a5)最小,其必要条件为
(13)
通过式(13)求取极值可以得到一个关于椭圆系数的多元函数线性方程组:
S′4i·Ai=H′i
(14)
又有:
(15)
(16)
(17)
由上述方程组可得拟合椭圆的系数向量Ai,则正余弦信号的误差补偿参数与椭圆系数向量Ai之间的关系可以表示为
(18)
式(18)中,M是由具体采样数据决定的常数,且:
(19)
在得到椭圆系数的唯一解之后,根据式(18)可以求出校正椭圆的全部误差参数,则由式(18)的关系式进一步推导可知,椭圆校正的误差参数可以用椭圆系数(a1,a2,a3,a4,a5)表示为
(20)
根据式(20)求得的误差参数Kx、Ky、b1、b2和φp,即可对存在幅值偏差、正交偏差和直流偏差的输出信号进行补偿,得到理想输出信号。
2.2 基于谐波分离算法的误差补偿
对于谐波误差,采用谐波分离的方法,通过交叉反馈网络分离基波分量和谐波分量,得到没有谐波污染的输出信号,从而计算出准确的角位置信息。
以只含有3次谐波为例,谐波分离法结构如图4所示。含谐波的输入信号可表示为
(21)
式中:u1、u3为基波和谐波的幅值;θ为转子位置角。
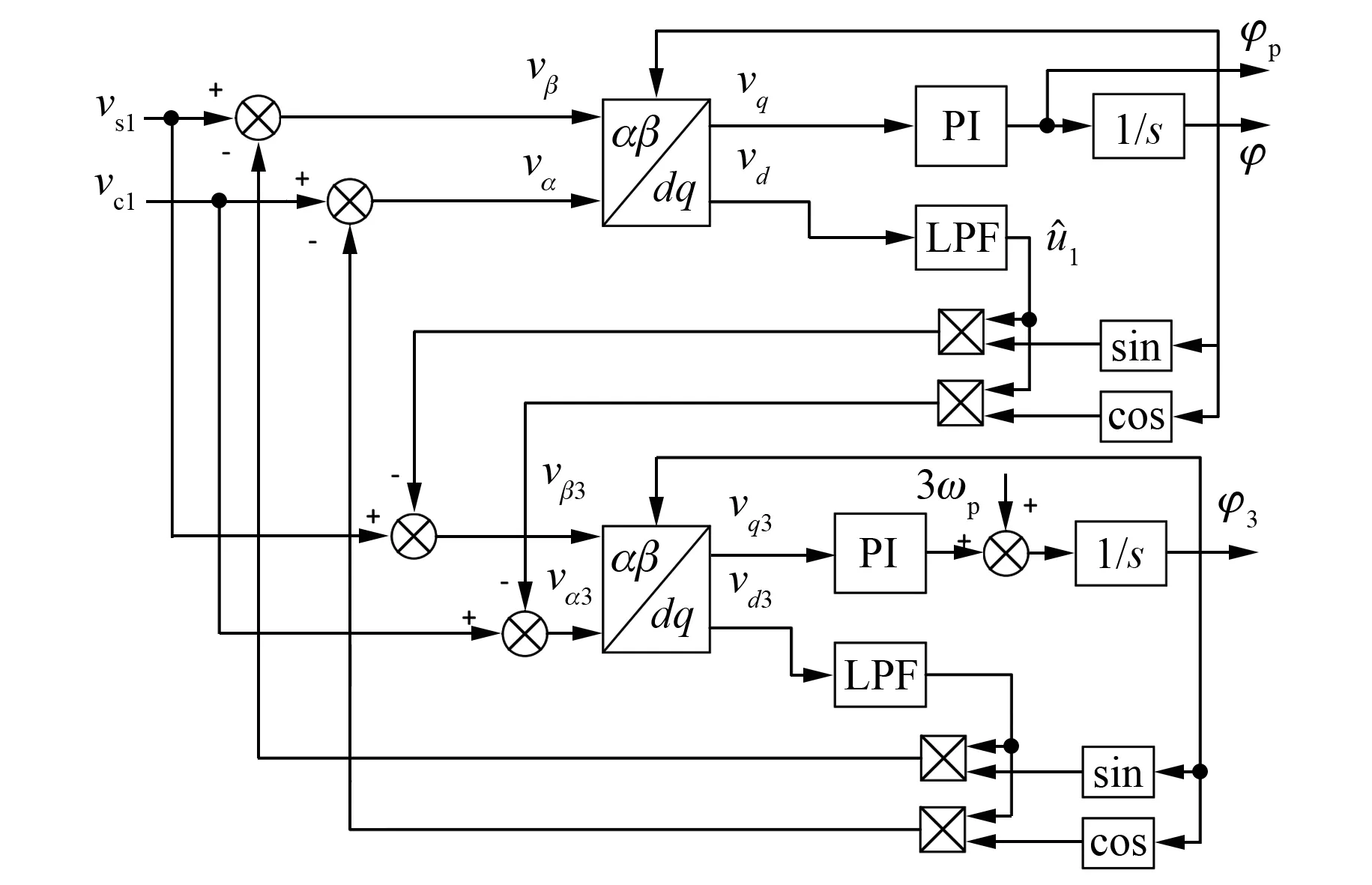
图4 谐波分离法结构框图
对输入信号进行Park变换,输出的d轴分量vd为信号的幅值,当经过低通滤波器以后,与锁相环(PLL)输出的转子角φ正余弦值相乘,即可得到基波分量。输入信号再减去基波分量,即可得到3次谐波分量,实现了3次谐波的分离。将3次谐波通过PLL输出角度φ3,使用同样的方法在输入信号中减去3次谐波分量而分离出基波分量:
(22)
(23)
在式(18)和式(19)中,通过谐波分离的方法使得每个PLL的输入信号均只含一个阶次的分量。若要同时去除3次谐波和5次谐波,只需要再增加5次谐波对应的PLL对其进行分离。
3 仿真与试验
3.1 仿真验证椭圆算法和谐波分离法
对上述基于最小二乘法的椭圆假设算法进行仿真分析,设定电机转速为1 500 r/min,给定正弦信号幅值误差α=0.1,直流偏置误差β=0.2,非正交的相位差弧度σ=0.2。根据椭圆假设算法估算所得结果如表1所示。
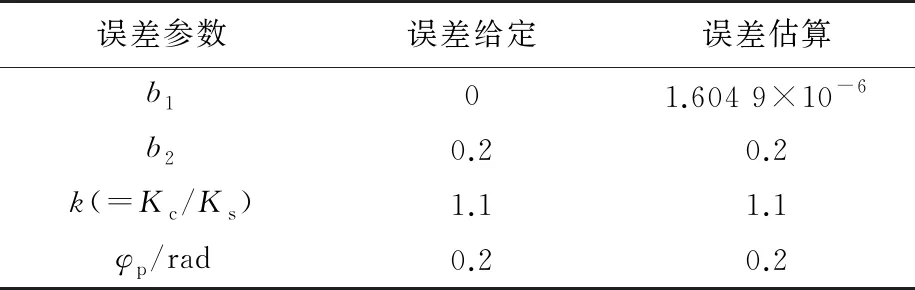
表1 1 500 r/min时误差系数估算前后对比
根据估算的误差值对输入正余弦信号进行补偿,补偿前后输入信号的Lissajou图形如图5所示。
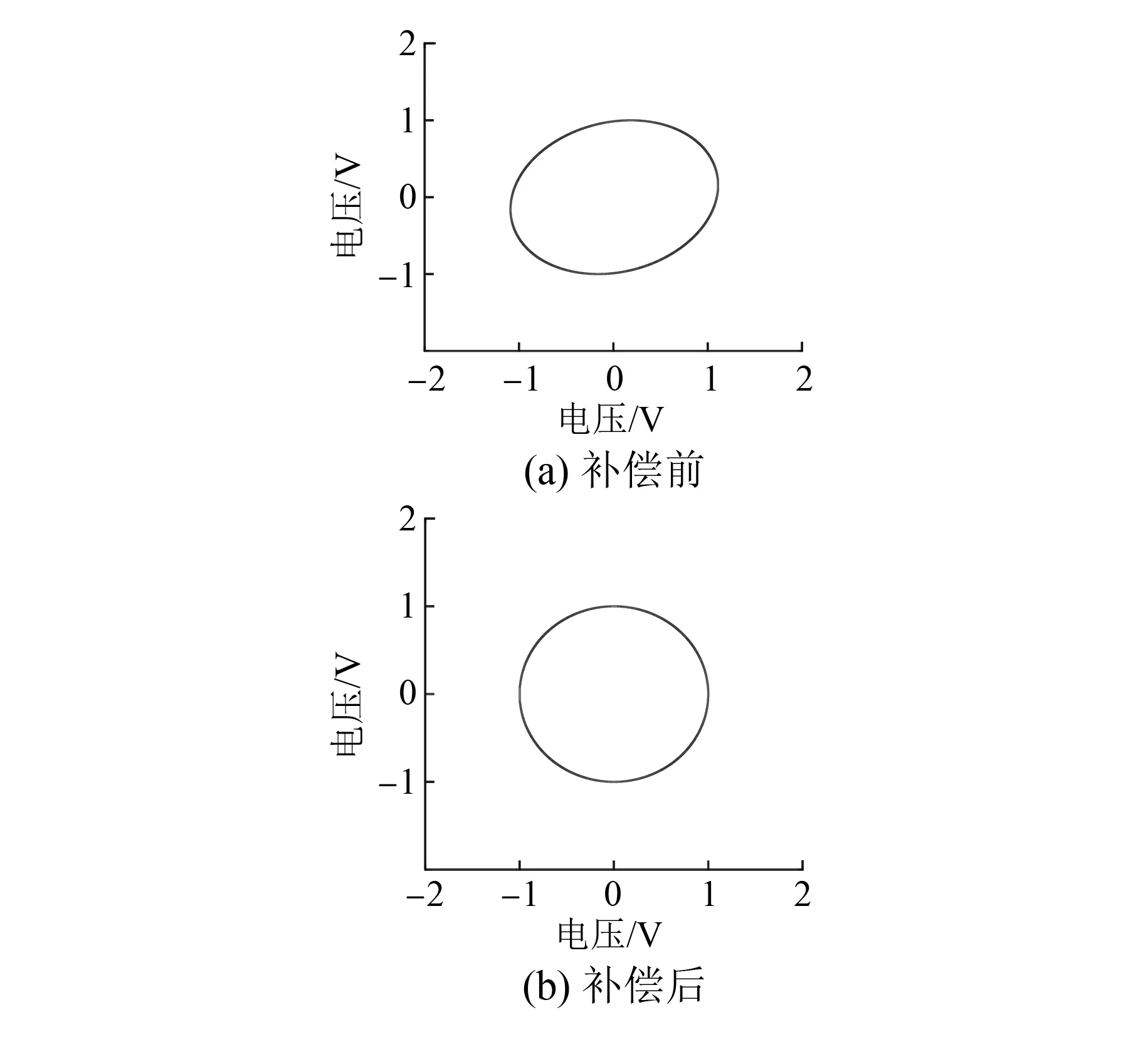
图5 输入信号Lissajou图
从仿真结果可知,采用最小二乘法的椭圆假设算法在电机恒速状态可达到精确的误差解算结果。
对谐波分离法进行仿真分析,假设旋转变压器输出信号只含有基波和5次谐波,基波幅值为10 V,角频率为1 000 π rad/s,5次谐波幅值为1 V,进行仿真分析。
基波经过Park变换,d轴分量通过滤波器后波形如图6所示。稳定时,基波幅值为10 V,与设定基波幅值相等。5次谐波经过Park变换,d轴分量通过滤波器所得波形如图7所示。稳定后幅值为1 V,与设定谐波幅值相等。
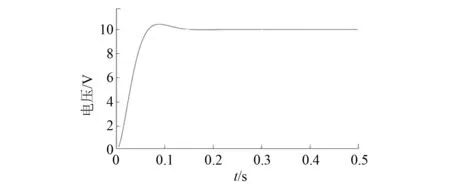
图6 基波幅值波形图
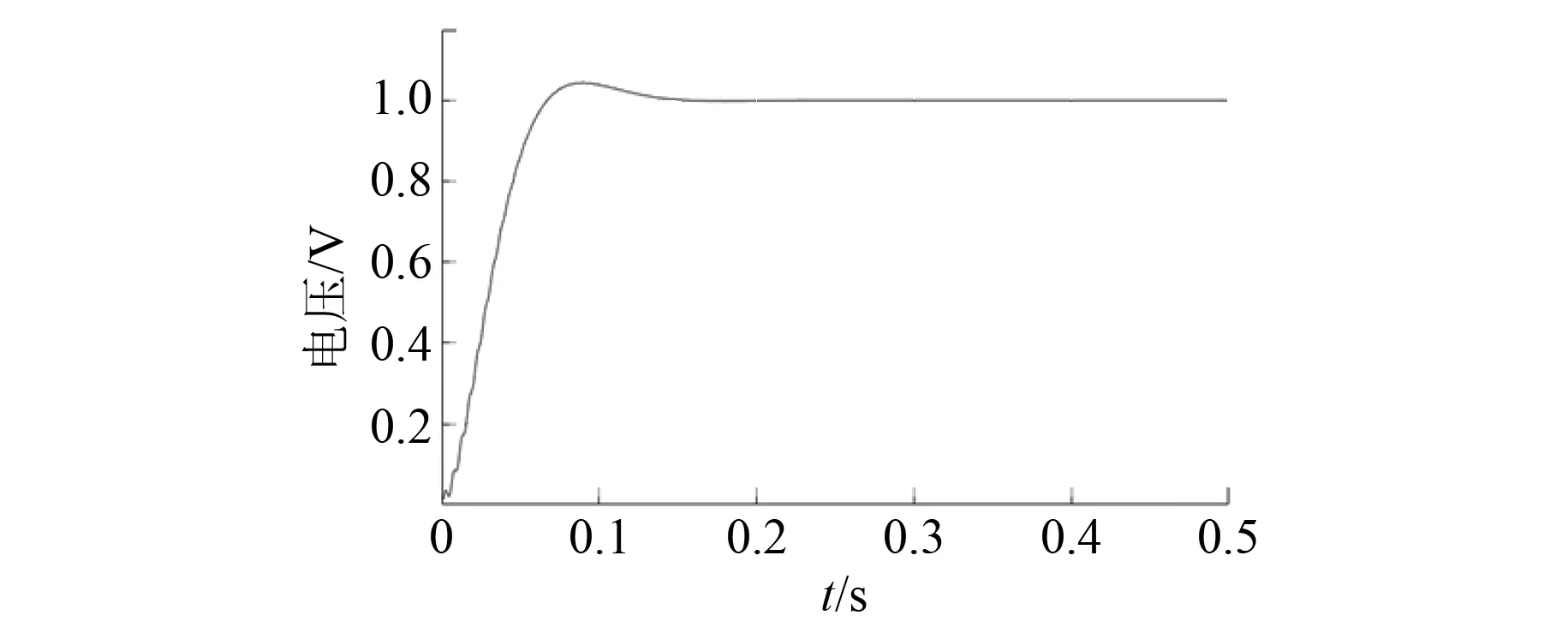
图7 五次谐波幅值波形图
补偿前和补偿后的正余弦信号波形如图8和图9所示。分离出的5次谐波波形如图10所示。由图8~图10可知,谐波分离法能够提取出谐波分量对输入信号进行补偿。
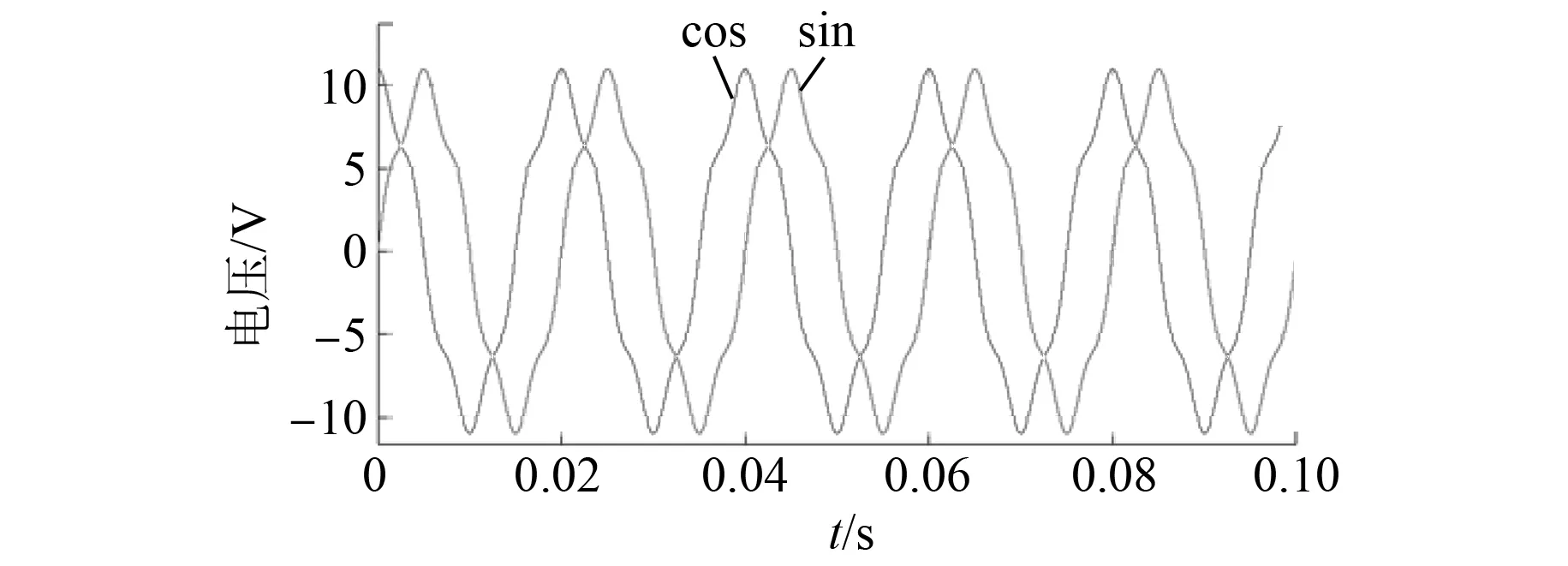
图8 补偿前正余弦信号波形图
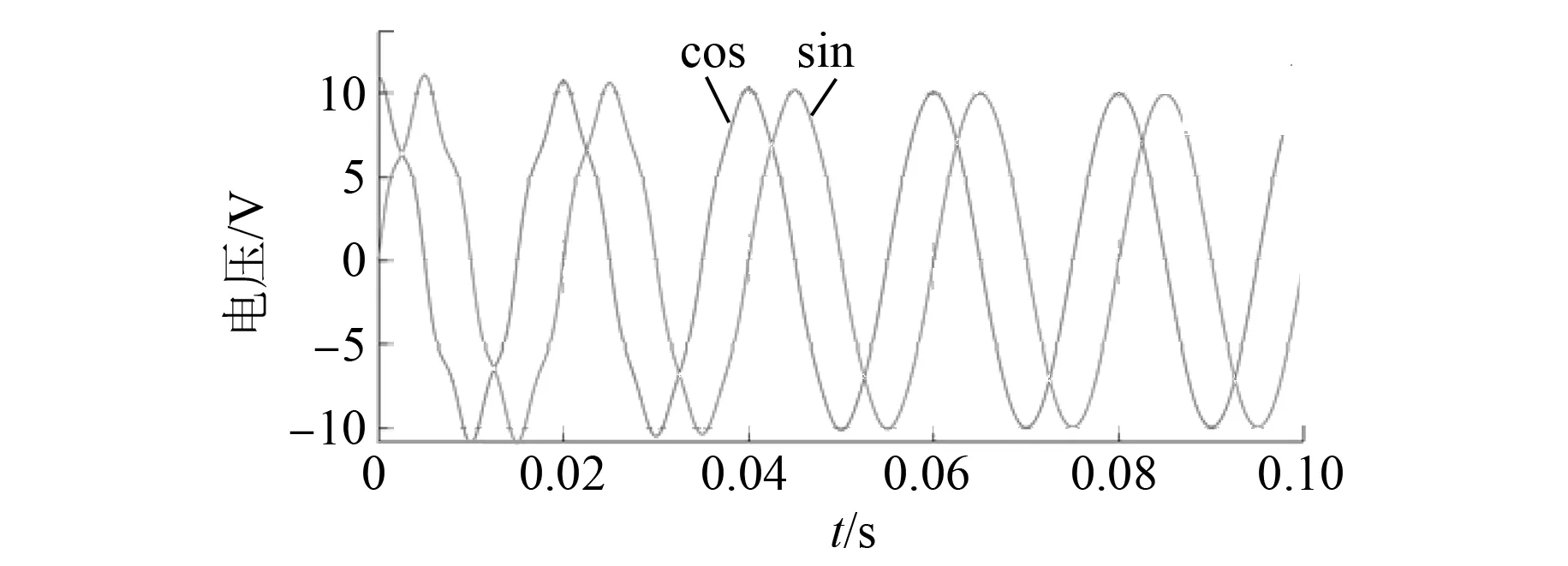
图9 补偿后正余弦信号波形图
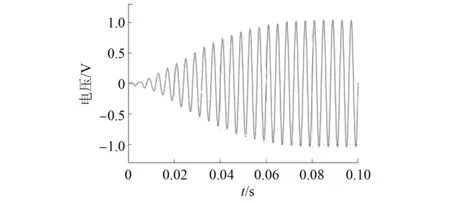
图10 分离出的5次谐波波形图
对信号中含有3次谐波和5次谐波进行仿真分析,基波幅值为10 V,角频率为1 000 πrad/s,3次谐波幅值为1 V,5次谐波幅值为0.5 V,在Simulink中搭建仿真模型。
基波经过Park变换,d轴分量通过滤波器所得波形如图11所示。稳定后为10 V,与设定幅值相等。3次谐波经过Park变换,d轴分量通过滤波器所得波形如图12所示。稳定后为1 V,与所设定3次谐波幅值相等。5次谐波经过Park变换,d轴分量通过滤波器所得波形如图13所示。稳定后为0.5 V,与所设定5次谐波幅值相等。
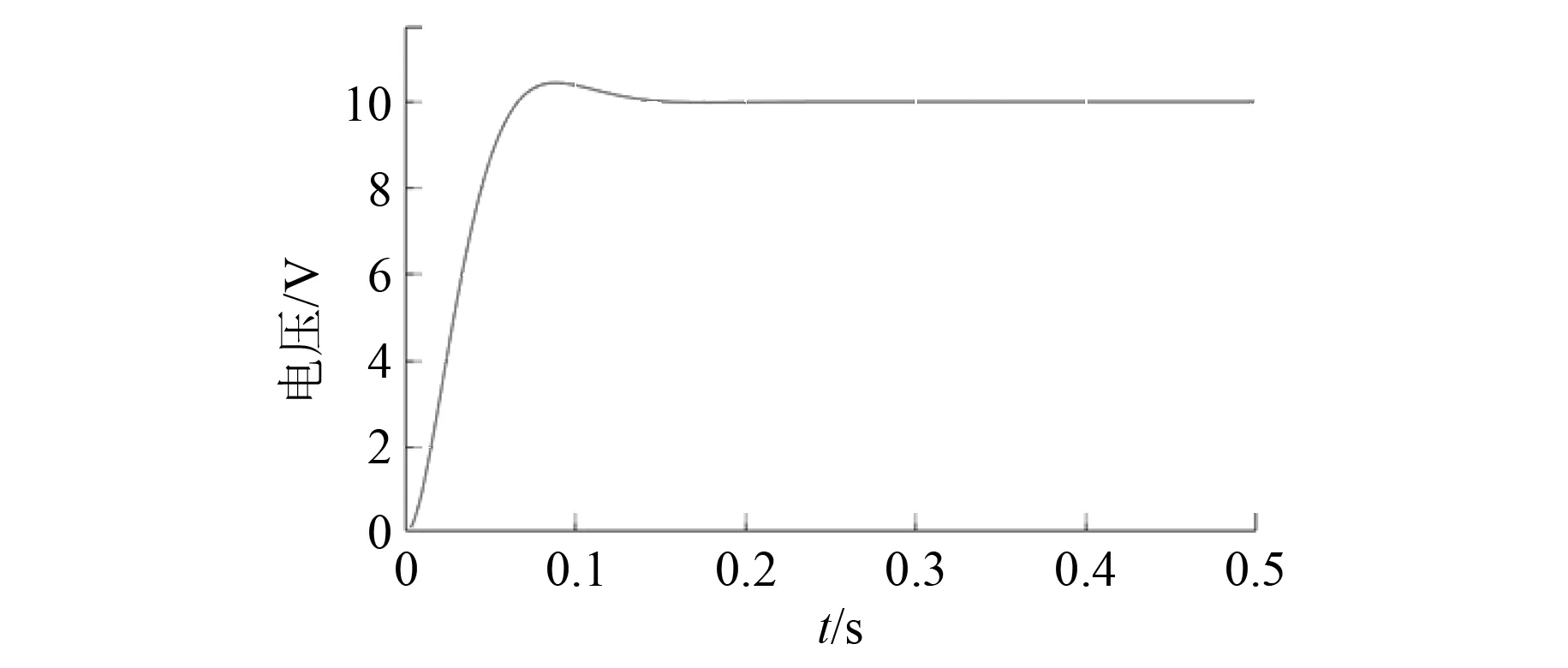
图11 基波幅值波形图
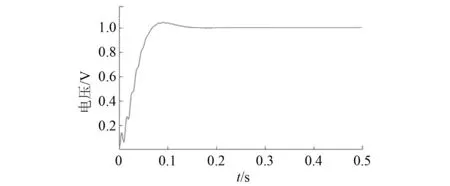
图12 3次谐波幅值波形图
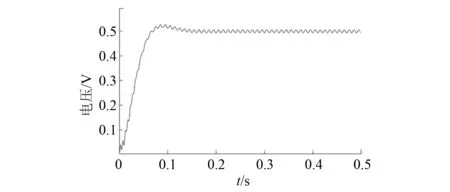
图13 5次谐波幅值波形图
补偿前后的正余弦信号波形如图14和图15所示,分离出的3次谐波波形和5次谐波波形如图16和图17所示。由图14~图17可知,在存在多个谐波分量的情况下,谐波分离法能够提取出谐波分量对输入信号进行补偿。
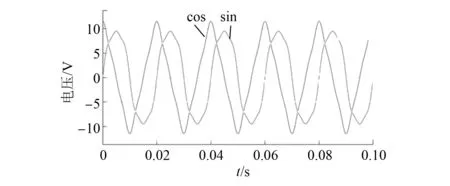
图14 补偿前正余弦信号波形图
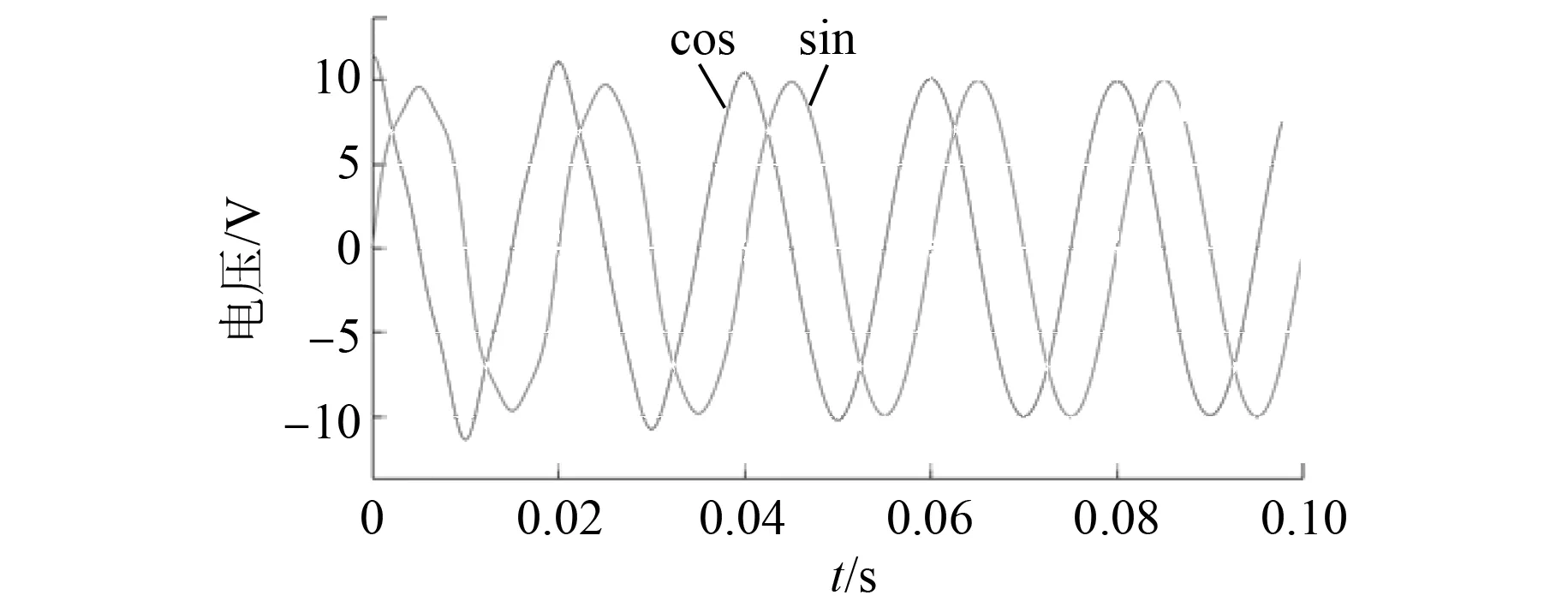
图15 补偿后正余弦信号波形图
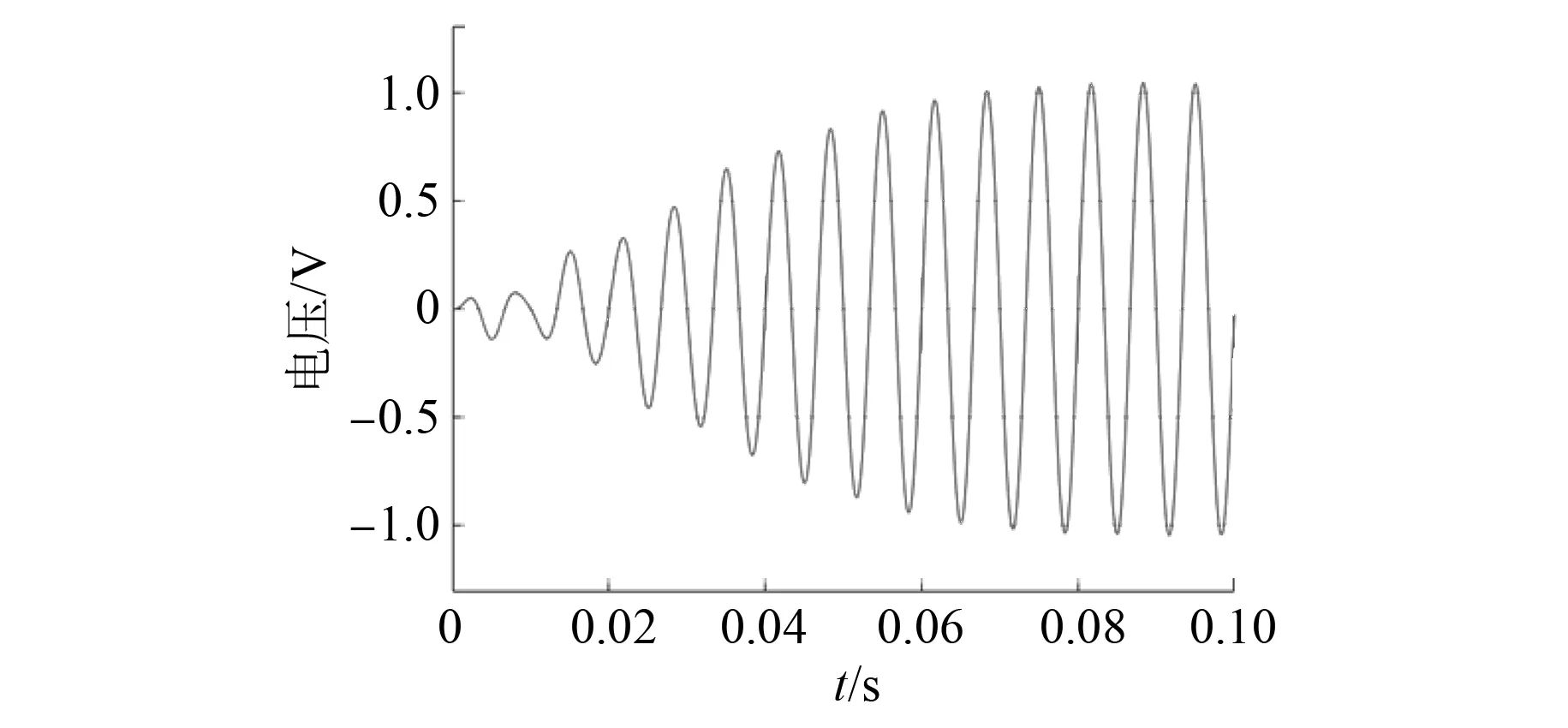
图16 分离出的3次谐波波形图
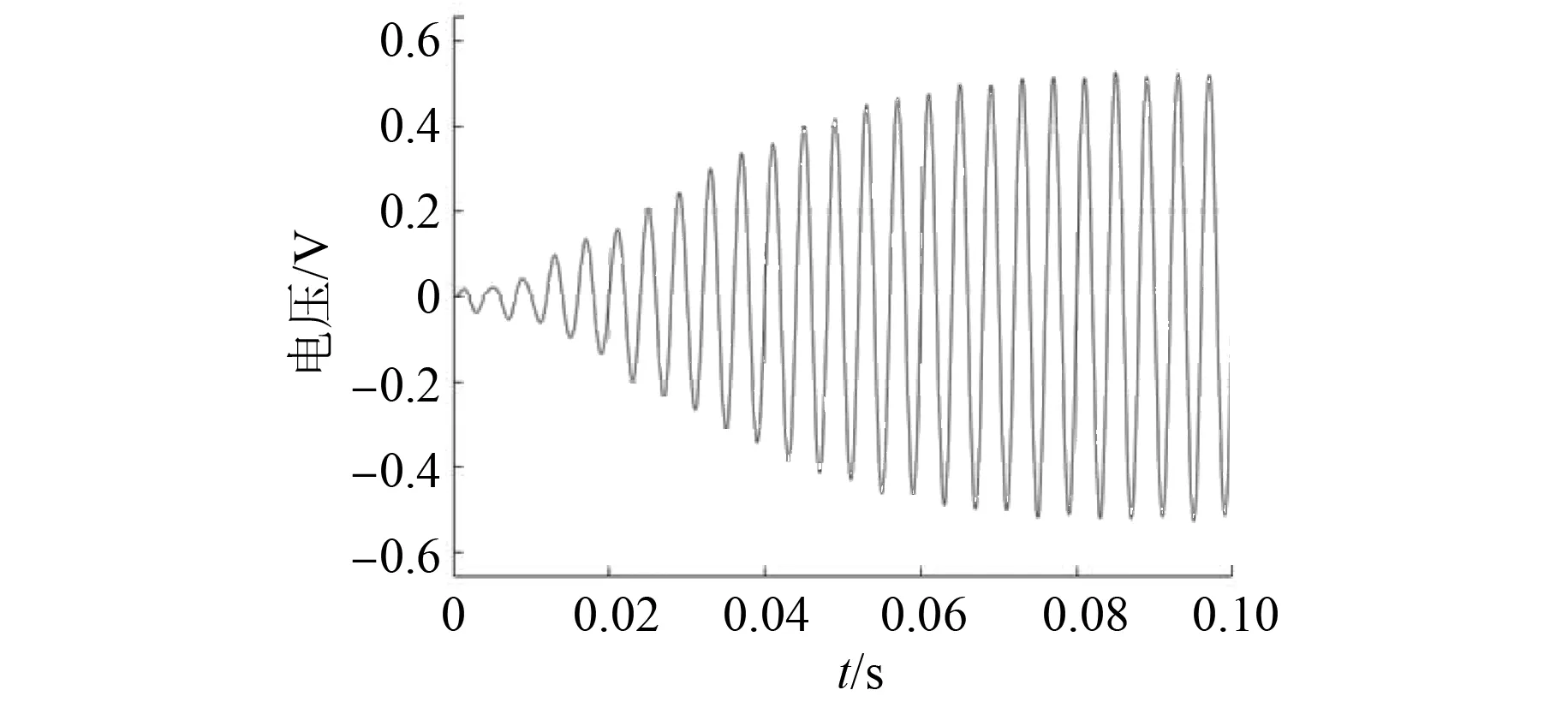
图17 分离出的5次谐波波形图
图18为未对谐波误差进行补偿和对谐波误差进行补偿时所得的转子位置波形图。可见,当对谐波误差进行补偿时,能够有效改善转子角测量精度。
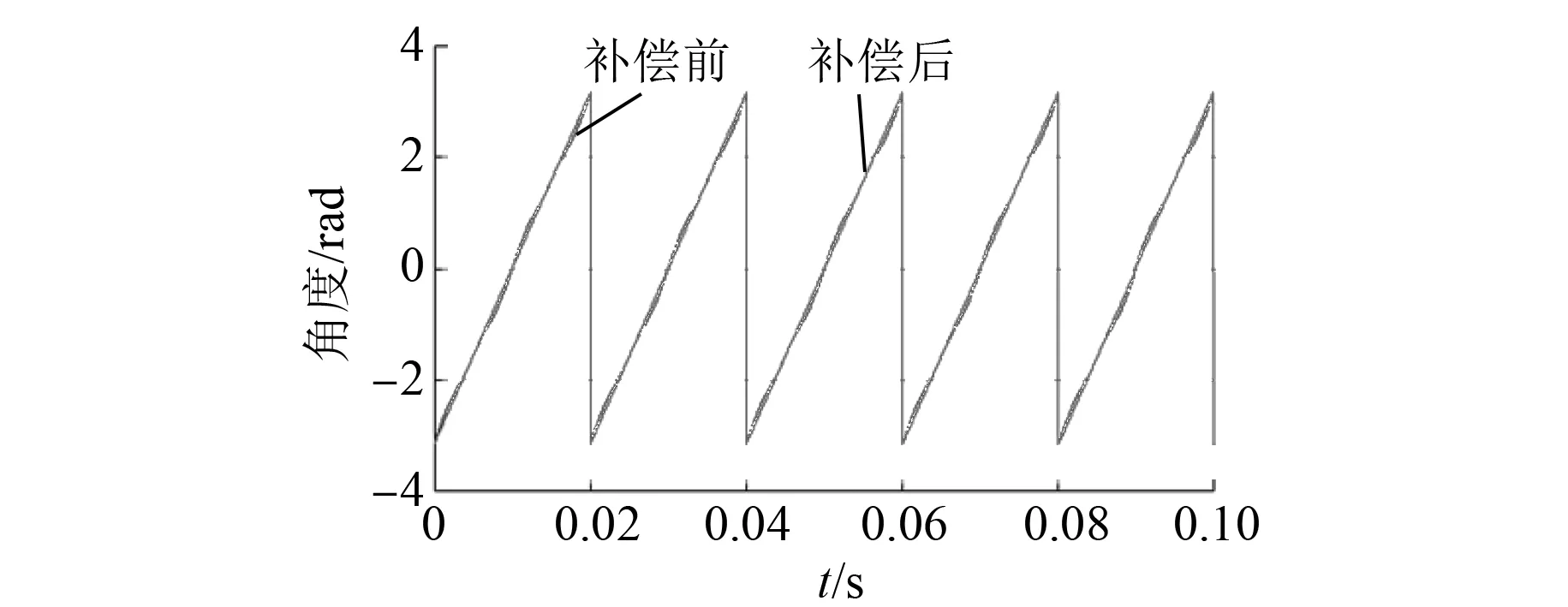
图18 补偿前后转子位置波形图
3.2 试验验证
对上述椭圆假设算法和谐波分离算法进行试验验证。图19为采用Vector公司高速测试工具VX1000记录的补偿前后的信号对比。当信号存在偏差时,幅度并不稳定,采用上述方法进行补偿以后,矢量幅度接近直线,由此验证了补偿方法的有效性。
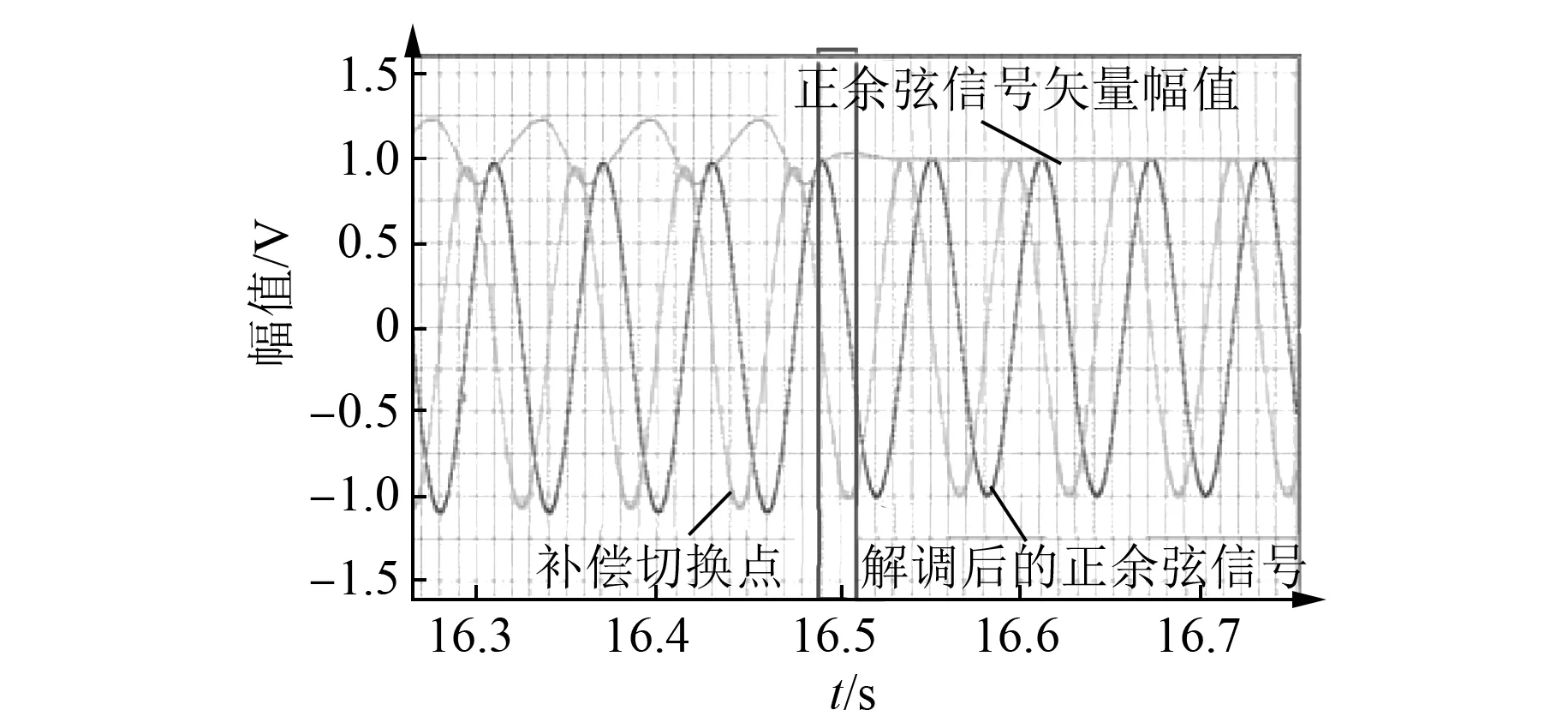
图19 原始信号与补偿后的信号对比
图20为实测带有信号补偿功能的RDC稳态误差,通过对比同轴的高精度编码器,可以得到RDC在50 r/min的稳态误差为1电角度(电机为4对极,旋转变压器为一对极),达到10位以上的角度测量精度。
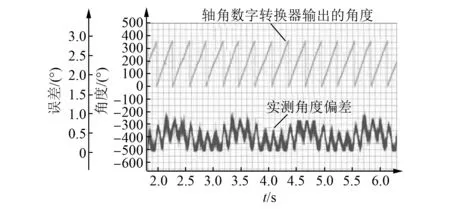
图20 补偿后RDC的稳态误差测试结果
图21为轴角数字转换器变化动态测试。可以看出,系统在2.3 s内从500 r/min到2 000 r/min加速过程,所有信号无畸变,速度采集超调较小,可以满足电机控制角度及速度测量的需求。
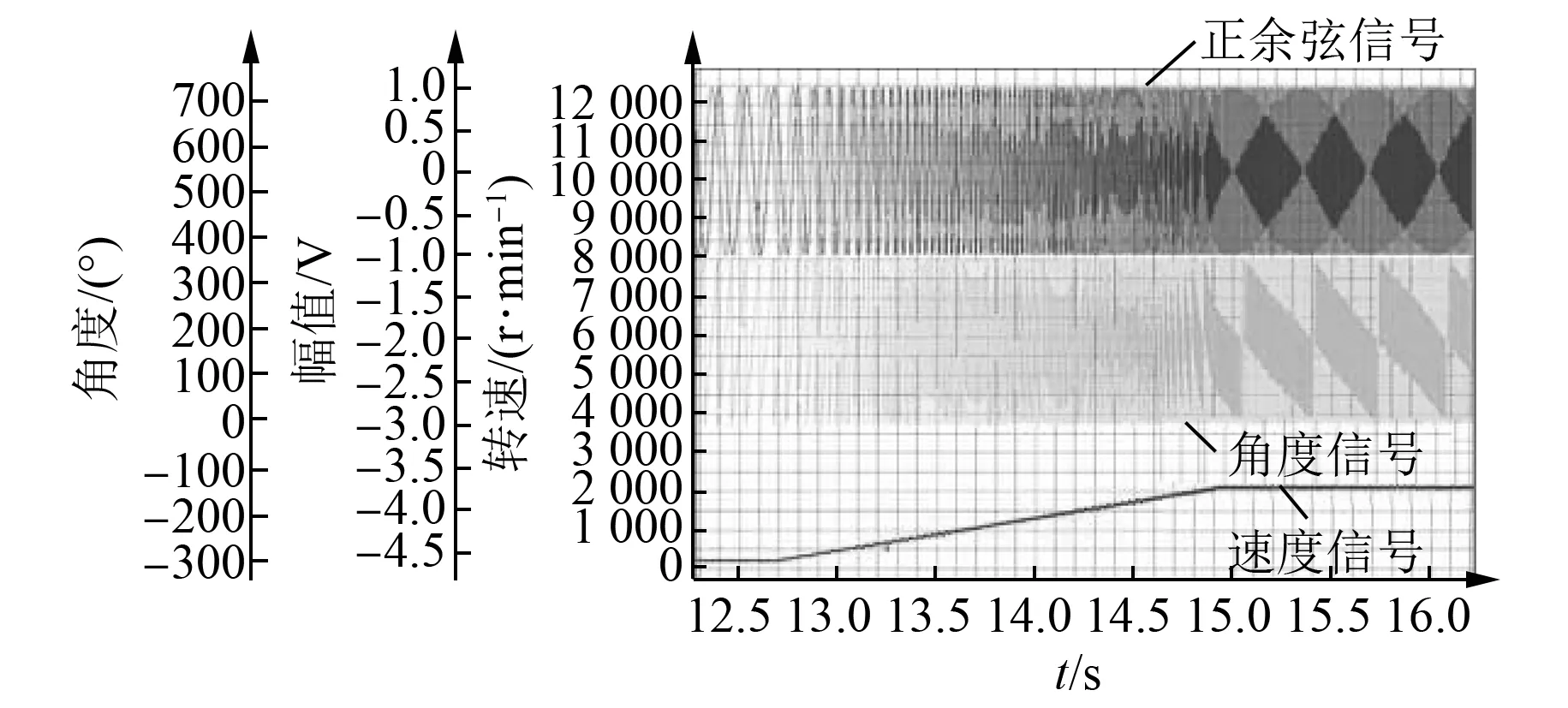
图21 RDC动态测试
4 结 语
本文研究了采用微处理器构成的数字RDC,采用基于SRF-PLL的位置角求解方法,滤除旋转变压器输出信号中的高频抖动分量。考虑了测角系统存在的误差,针对旋转变压器输出信号中的零位误差、正交误差和幅值误差的影响研究采用椭圆假设算法进行消除,并研究了谐波分离法来实现对信号中谐波误差的补偿。最后,搭建仿真模型和试验平台进行了分析验证。结果证明所提方法能够较为准确地在线检测到设备误差,对误差补偿后,能够改善系统的测角精度。

