分数槽永磁同步直线电机空载气隙磁密解析
刘文奇, 崔皆凡, 李柏昕, 郝景申
沈阳工业大学 电气工程学院, 辽宁 沈阳 110000)
0 引 言
永磁同步直线电机(PMSLM)发展迅速,因其质量轻、体积小、结构简单、无中间驱动装置、推力密度大、响应速度快等优势在机床进给系统、机器人,航空航天等领域得到广泛应用。其中,特别是分数槽永磁同步直线电机(FPMSLM),具有端部绕组短、铜耗小、转矩波动小等优点[1-3]。准确计算出PMSLM的气隙磁密是对其进行优化设计和性能分析的前提条件,国内外的许多学者利用多种方法对其进行了较为深入的研究。
目前广泛采用的方法有传统磁路法、有限元法、解析计算法[4-6]。文献[7]基于许克变换,借助许克变换工具箱分析了电机定子绕组产生的气隙磁场和永磁体产生的气隙磁场,该方法需要设计者精通许克变换工具箱的使用。文献[8]运用解析法获得电机磁场,但气隙磁导函数采用了相应的替代函数。文献[9]用傅氏级数法推导出FPMSLM的气隙磁场,虽然解析法和有限元法具有良好的拟合度,但利用分布卡氏系数计算铁心开槽对分数槽电机磁场的影响,增加了计算的复杂度。文献[10]将电机细分成多个求解区域,进而获得整个电机的磁场分布情况,此类方法可获得较高计算精度,但其求解过程较为复杂,不利于电机性能的快速分析。
对于FPMSLM,每个磁极下气隙磁场并不相同,因此不能只计算一对极下的气隙磁场。本文以单元电机整体为研究对象,对定子不开槽下的气隙磁场进行计算,再考虑定子开槽影响下的气隙磁密,推导了FPMSLM定转子整体耦合长度下任意位置的空载气隙磁场解析式,最后以2台单元电机,即10极 9槽、10极12槽FPMSLM为例,对其空载气隙磁场进行有限元仿真。将有限元法结果与解析法结果进行对比分析,验证了解析法计算空载气隙磁密的可行性,节约了时间成本,为FPMSLM空载气隙磁场的优化提供了理论支持。
1 PMSLM的气隙磁场分析
1.1 单元电机的基本概念
分数槽绕组产生的磁动势波形不是以每对极为一个重复周期,而是以一个单元电机为一个重复周期,因此在一个周期内每极所占槽数不同。对FPMSLM来说,其每极每相槽数q如下:
(1)
式中:Z为槽数;p为极对数;m为相数;F、d为经计算化简之后,所得最简分式的分子与分母。
当d为偶数时,单元电机的磁极数为d;当d为奇数时,单元电机的磁极数为2d。
1.2 气隙磁场基本关系式
本文对FPMSLM空载气隙磁场的解析表达式进行推导计算定子不开槽情况下永磁体磁密方波的解析式。
在定子不开槽的时候,气隙是均匀分布的,因此气隙中单位面积的磁导为
(2)
式中:δ为定子不开槽时永磁体磁化方向长度与气隙长度之和。
又有:
δ=hm+δ0
(3)
式中:hm为永磁体磁化方向长度;δ0为气隙长度。
在定子开槽的情况下,气隙是周期性均匀变化的,此时气隙中单位面积的磁导为
Λ(x)=μ0/δ(x)
(4)
式中:δ(x)为定子开槽时随位置周期变化的气隙长度。
定子开槽情况下,永磁体产生的气隙磁密表达式为
(5)
式中:B(x)为定子开槽下的空载气隙磁密;Bδ(x)为定子不开槽下的空载气隙磁密。
1.3 定子不开槽时的气隙磁场分布
在进行气隙磁密解析式推导前,需要作以下3点假设:
(1) 铁心冲片材料各向同性, 且磁化曲线是单值的;
(2) 忽略铁心的涡流效应以及磁滞效应;
(3) 永磁体的磁导率与空气磁导率相同。
以单元电机为例,因为每极下气隙磁场不同,不能单独推导一对磁极下的气隙磁场,所以把整个磁极看作一个整体,分成极对数为奇数或偶数2种情况。图1为极对数为奇数时FPMSLM气隙磁密分布图。坐标原点选在单元电机的极中心点。
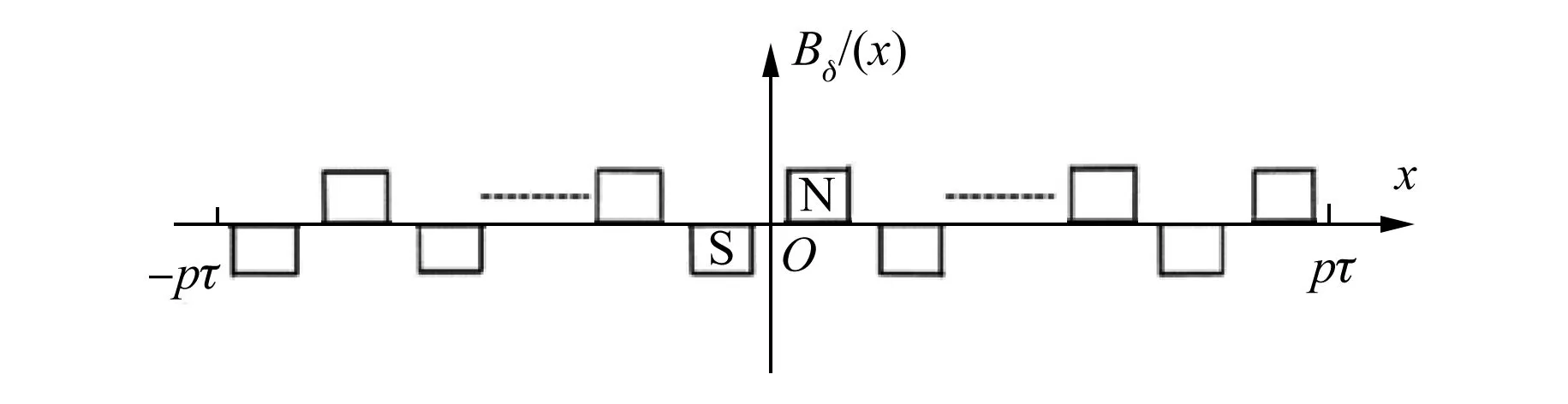
图1 极对数为奇数时定子不开槽气隙磁密分布
在x∈[-pτ,pτ]区间内,气隙磁密的表达式如下:
Bδ(x)=
(6)
式中:τ为极距;αi是计算极弧系数,k=0,±1,…,±[p/2]。
Bδ永磁体产生的方波气隙磁密的幅值:
Bδ=Brhm/δ
(7)
式中:Br为永磁体剩磁。
由于Bδ(x)为奇函数,表示成傅里叶级数形式如下:
(8)
(9)
可得:
x∈[-pτ,pτ]
(10)
图2为极对数为偶数时FPMSLM气隙磁密分布图。坐标原点选在单元电机的极中心点。
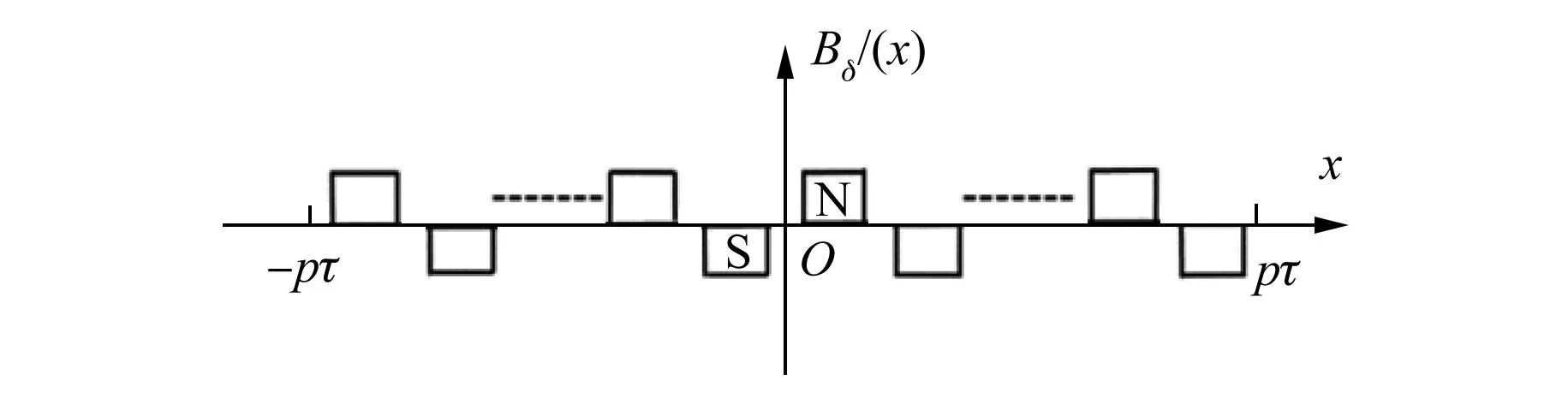
图2 极对数为偶数时定子不开槽气隙磁密分布
在x∈[0,Zt/2]区间内,气隙磁密表达式为
Bδ(x)=
(11)
其中,k=0,±1,…,±[p/2]。
对其进行傅里叶变换,得定子不开槽,则极对数为偶数时永磁体产生的气隙磁密如下:
x∈[-pτ,pτ]
(12)
对比式(10)和式(12)可以看出,极对数为奇数与极对数为偶数的单元电机,在定子不开槽情况下,其表达形式相同。由此可得,单元电机定子不开槽情况下,气隙磁密表达式为
x∈[-pτ,pτ]
(13)
2 定子开槽空载气隙磁场分布
定子开槽后,由永磁体产生的气隙磁场会发生变化。把整个槽数看作一个整体,分成槽数为奇数或偶数2种情况。图3为定子开槽后,单元电机槽数为奇数时等效气隙长度随x的变化情况。坐标原点选在整个单元电机的槽中心点。
(14)
式中:hs为槽深;t为齿距;b为槽宽。
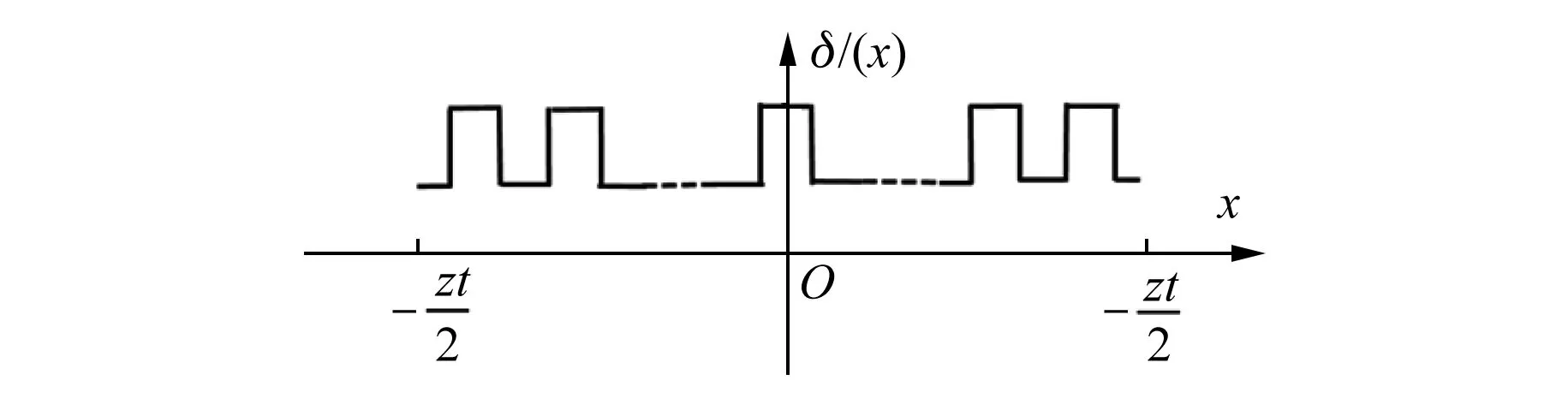
图3 槽数为奇数时气隙长度分布图
式(14)气隙长度随x的变化规律如下:
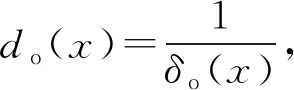
(15)
式中:w为齿宽,k=0,±1,…,[Z/2]。
其傅里叶分解表达式为
(16)
其中,
(17)
(18)
(19)
由Bo(x)=δBδ(x)do(x)可得,奇数槽FPMLSM的气隙磁密表达式为
x∈[-Zt/2,Zt/2]
(20)
单元电机的槽数为奇数时任意位置下的定转子耦合部分气隙磁密解析式为
x∈[-Zt/2,Zt/2]
(21)
式中:l1为极中心线相对于齿中心线向左偏移的距离。
图4为定子开槽后,单元电机槽数为偶数时等效气隙长度随x的变化情况。坐标原点选在整个单元电机的槽中心点。
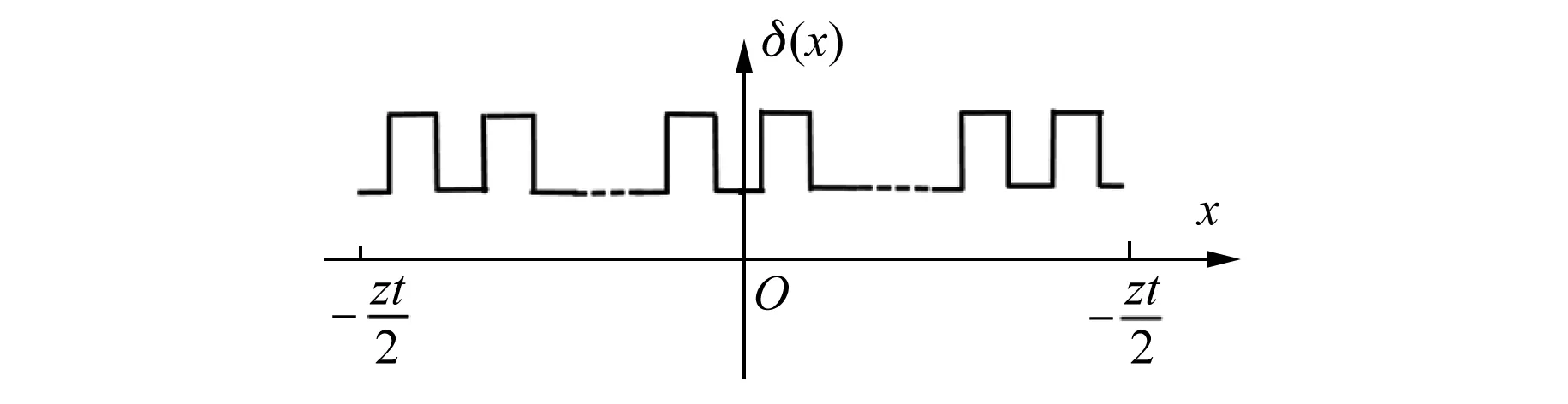
图4 槽数为偶数时气隙长度分布图
槽数为偶数时d(x)的求解同理于槽数为奇数时d(x)的求解,得:
(22)
当槽数为偶数时,FPMSLM的空载气隙磁密表达式为
x∈[-Zt/2,Zt/2]
(23)
单元电机的槽数为偶数时任意位置下定转子耦合部分的气隙磁密解析式为
x∈[-Zt/2,Zt/2]
(24)
式中:l2为极中心线相对于齿中心线向右偏移的距离。
由此可以看出,定子开槽后,改变了原本定子不开槽下的气隙磁密次数和幅值。
3 解析法与有限元法对比
为了验证气隙磁场解析式推导的有效性, 选取2台FPMSLM,即10极12槽FPMSLM、10极9槽FPMSLM,进行气隙磁场解析计算。
10极12槽FPMSLM的永磁体磁化方向长度hm=7 mm,极弧系数αi=0.858,齿距t=17 mm,槽宽b=9 mm,极距τ=20.4 mm,气隙长度δ0=1 mm。同时利用解析法与有限元法对其气隙磁场进行计算。
图5为开口槽结构10极12槽FPMSLM结构图。 该FPMSLM的极中心线相对于齿中心线右移18.4 mm。

图5 开口槽结构10极12槽FPMSLM结构图(单位:mm)
图6为电机处于图5位置时,电机空载气隙磁密解析法与有限元法结果对比。
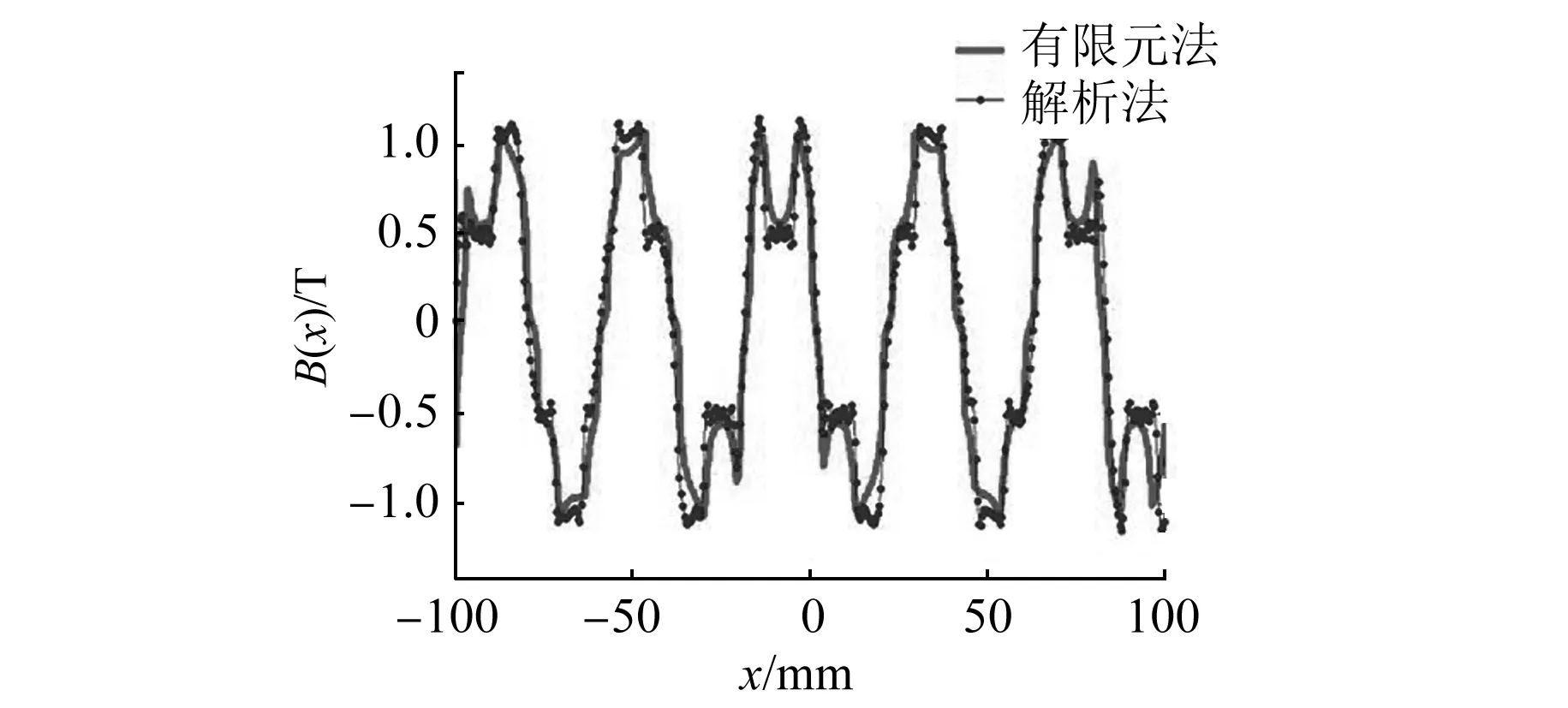
图6 电机处于图5位置时,电机空载气隙磁密解析法与有限元法结果对比
由图6可得,解析法可以较为准确地反映FPMSLM的空载气隙磁场。2种方法也反映了开口槽结构FPMSLM气隙磁场谐波含量大的问题。因此,在实际工程应用中一般采用闭口槽结构。
利用解析法和有限元法同时对半闭口槽结构的10极12槽FPMSLM空载气隙磁密进行计算。
图7为半闭口槽结构10极12槽FPMSLM结构图,极中心线与齿中心线对齐。
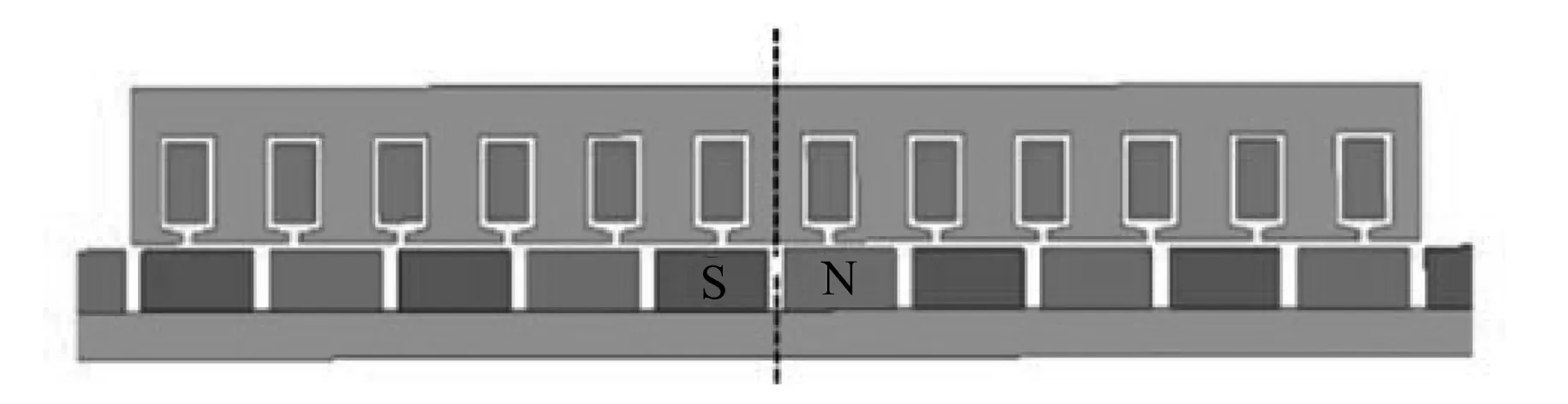
图7 半闭口槽结构10极12槽FPMSLM结构图
图8为半闭口槽10极12槽FPMSLM空载气隙磁密解析法与有限元法计算结果对比。
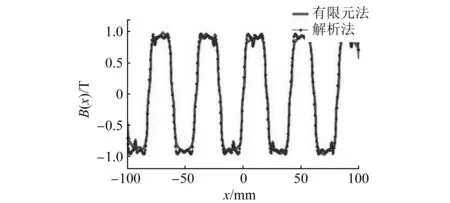
图8 半闭口槽10极12槽FPMSLM空载气隙磁密解析法与有限元法计算结果对比
由图8可得,解析法计算同样可以反映半闭口槽10极12槽FPMSLM的空载气隙磁密。
10极9槽FPMSLM的永磁体磁化方向长度hm=7 mm,极弧系数αi=0.858,齿距t=22 mm,槽宽b=14.03 mm,极距τ=20.4 mm,气隙长度δ0=1 mm。同时利用解析法与有限元法对其气隙磁场进行计算。
图9为开口槽结构10极9槽FPMSLM结构图。该FPMSLM的极中心线相对于齿中心线右移10 mm。
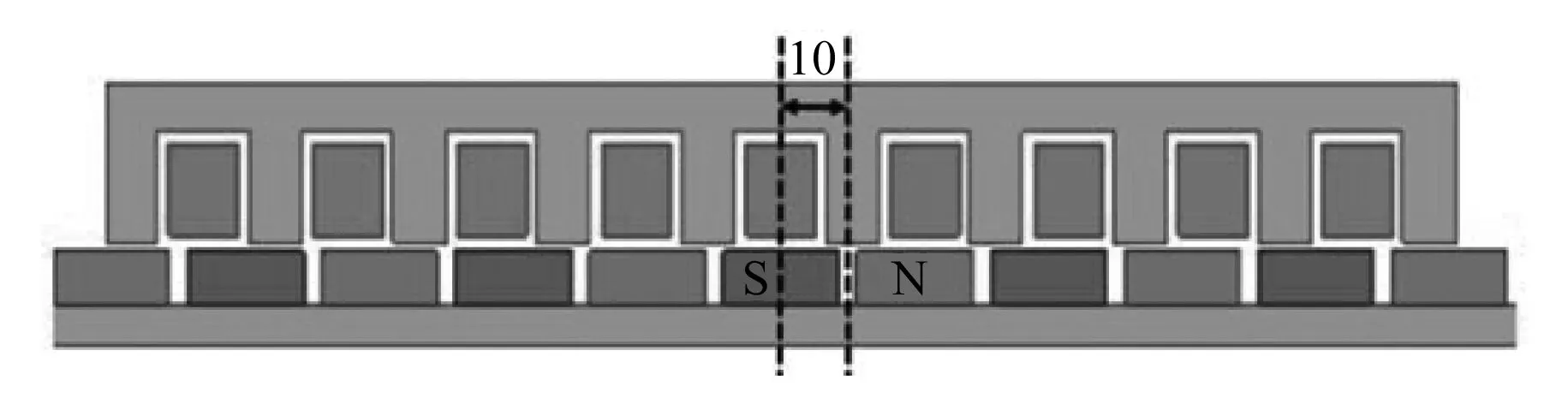
图9 开口槽结构10极9槽FPMSLM结构图(单位:mm)
图10为电机处于图9位置时,电机空载气隙磁密解析法与有限元法结果对比图。

图10 电机处于图9位置时,电机空载气隙磁密解析法与有限元法结果对比
图11为半闭口槽结构10极9槽FPMSLM结构图,极中心线与齿中心线对齐。
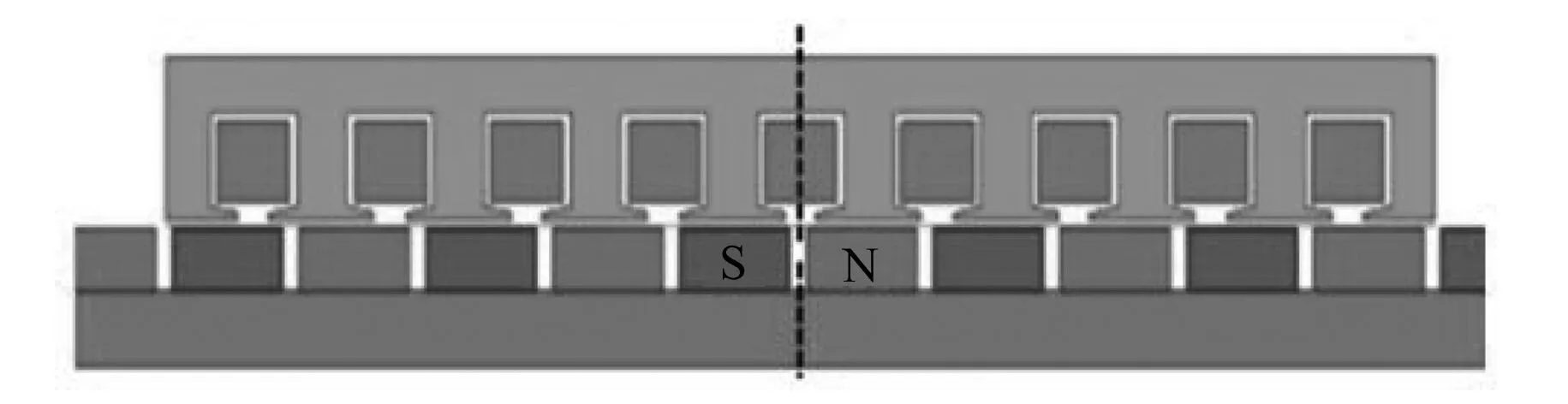
图11 半闭口槽结构10极9槽FPMSLM结构图
图12为半闭口槽10极9槽FPMSLM空载气隙磁密解析法与有限元法计算结果对比。

图12 半闭口槽10极9槽FPMSLM空载气隙磁密解析法与有限元法计算结果对比
表1为解析法与有限元法的基波幅值及其误差对比。表2为解析法与有限元法的3次谐波幅值及其误差对比。

表1 解析法与有限元法基波幅值对比
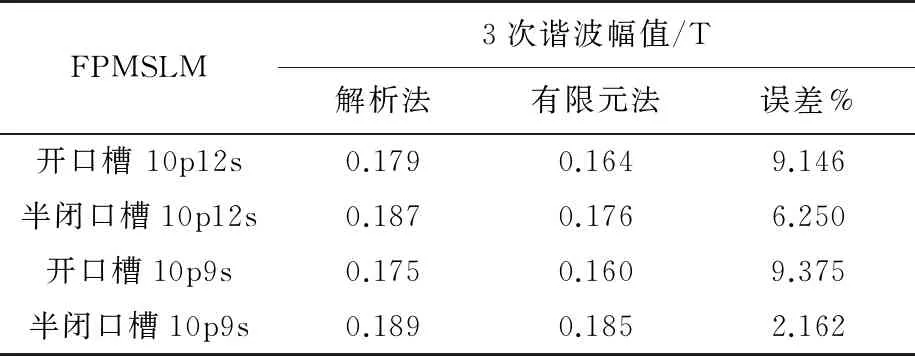
表2 解析法与有限元法3次谐波幅值对比
由表2的数据可知,解析法与有限元法存在误差。在实际情况中,由于铁心磁导率远大于气隙,受媒质突变和边缘效应的影响在槽口边沿处磁密会出现短距离的激增现象,而解析法不存在磁密突增的情况;解析法在计算过程中,磁力线垂直槽底,而有限元法中,磁力线在槽中转向槽壁,这2点均是解析法比有限元法存在误差的原因。
4 结 语
本文采用解析计算的方法,对FPMSLM的空载气隙磁密进行了分析和计算,得出FPMSLM的空载气隙磁密解析式。并以2单元电机, 即10极12槽、10极9槽FPMSLM为例,分别用解析法和有限元法对电机的空载气隙磁密进行计算,计算了解析法与有限元法所得结果的误差。误差的主要原因为,当解析法计算时,槽深为实际槽深,而实际情况下,磁力线并不会垂直指向槽底,可通过经验系数来计算等效槽深,以此减小误差。解析法给出了FPMSLM空载气隙磁场与电机结构尺寸的直接关系式,与有限元方法相比,解析法提高了计算速度,降低了计算的规模,节约了时间成本,为进一步分析FPMSLM的工作特性提供了参考。

