基于ASAPSO的火炮随动系统模糊控制策略
王继超, 冷育明, 戚延辉, 王 磊
中国人民解放军31696部队,辽宁 锦州 121000)
0 引 言
进入21世纪以来,交流伺服技术与智能控制相结合,使得永磁同步电机(PMSM)在各个领域得到了广泛的应用。在速度控制和位置控制上,以PMSM为主的交流伺服系统已成为主流,在工业领域和军事技术等方面均取得了突出的效益。当前,地面火炮控制系统仍采用直流有刷电机作为执行元件。从控制效果看,不仅响应速度慢,而且定位精度一般。因此,从提高武器装备性能的角度出发,将交流伺服系统应用于火炮随动跟踪控制系统势在必行。
PMSM作为执行元件,应用于火炮随动系统上,必须适应随动系统转动惯量大、位置变化无规律、响应速度快、定位精度高的特点[1]。因此,位置控制器的设计要求必须高。
与常规PID控制方式相比,模糊控制算法并不需要对被控系统建立数学模型。PMSM具有非线性特点,作为火炮随动系统执行元件时,常规的PID 控制方式难以跟随系统变化,对火炮随动跟踪系统的控制达不到要求。而模糊控制器在解决这一问题时,效果大大优于PID控制器。
模糊控制器性能的好坏,主要取决于4个参数,分别为3个量化参数和1个模糊规则权值[2]。因此,为了保证火炮随动跟踪系统的速度和精度,本文采用自适应模拟退火粒子群算法(ASAPSO)对这4个参数进行优化。通过仿真,对比了模糊控制器和传统PID控制器在火炮随动跟踪系统中的控制效果[3]。
1 系统结构
1.1 火炮随动跟踪系统基本模型
火炮随动跟踪系统由视频跟踪器、瞄准线控制器、执行机构和相应的传感器组成。图1为独立稳定的瞄准线控制系统结构图[4]。
图1中,目标位置θi与瞄准线位置θo的差值送给视频跟踪器,x为跟踪误差,M为执行机构的控制力矩。其中,执行机构用来带动火炮身管高低方向运动。系统采用PMSM替代传统直流电机,是本文研究的重点对象。
1.2 控制系统结构和模型的建立
以PMSM替代传统的无刷直流电机作为系统的执行机构,构建空间矢量模型。控制模块采用dsPIC33F来实现空间矢量控制脉宽调制(PWM)[5]。搭建三闭环位置控制系统如图2所示。
该随动控制跟踪系统的模型大致由以下5个模块构成:
(1) 角度偏差传感器模块;
(2) PI调节器;
(3) 坐标变换模块;
(4) 空间矢量PWM(SVPWM)模块;
(5) 模糊控制器。
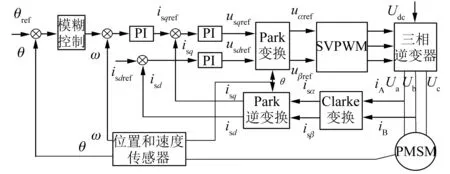
图2 交流伺服系统三闭环矢量控制系统模型
控制过程为:目标位置与瞄准线位置的差值经视频跟踪器处理后得出跟踪误差x。模糊控制器放在系统位置环上,输出速度信号。q轴电流分量由速度PI调节器调节误差信号后得出,d轴电流分量为设定值零。q轴和d轴电流分量经坐标变换后,得到相电压分量并通过SVPWM技术,产生PWM信号。控制IGBT模块,逆变输出可变频率的三相正弦电压输入到电机定子,达到控制的目的[6]。
2 模糊控制器
2.1 模糊控制器的组成和原理
模糊控制系统的基本工作原理可以用图3来表示。控制过程为:单片机对被测对象进行采样并进行A/D转换,与给定值进行比较,从而得到误差e。误差e经过模糊化处理后,代入已经制定好的模糊控制规则,做出模糊决策,输出控制量u。图中虚线框内的模糊控制器是核心部分,模糊控制规律可以通过计算机程序设定[7]。
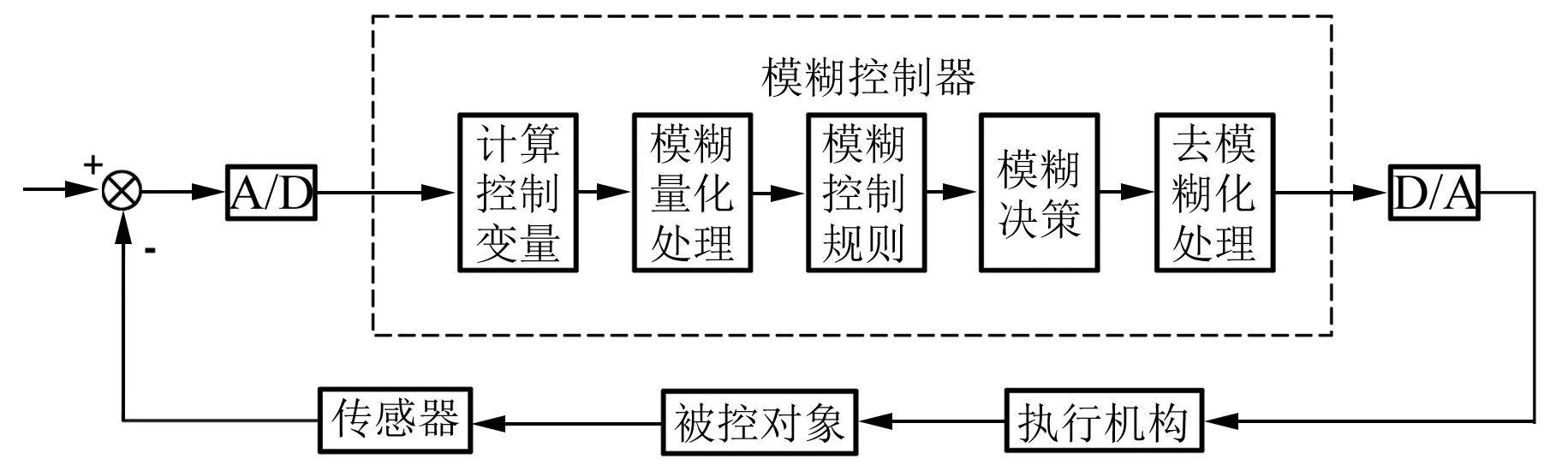
图3 模糊控制系统原理图
对于火炮随动跟踪系统,图3中的被控对象就是火炮身管,执行机构采用PMSM,传感器采用增量式编码器。模糊控制器通过编写程序设定在控制系统中。其主要由4个部分组成:模糊化接口、知识库、模糊推理和去模糊化。
2.2 模糊控制器的设计
2.2.1 模糊化接口
将测得的目标实际位置和火炮瞄准线位置相比较,得到误差信号e。该信号和变化量ec设定为2个输入量,执行机构给出的身管转动速度u作为输出量。将误差e、误差变化率ec和转速u进行尺度变换,统一采用归一化处理,即e∈[-1,1],ec∈[-1,1],u∈[-1,1]。
输入量e、ec和输出量u的隶属度函数选择三角形隶属度函数[8]。隶属度函数形状及配置均按图4所示设置。为了更好地描述三角形分布特点,反映隶属度函数的控制规律,引入间隔参数sp,间隔参数的大小反映的是三角形顶点的分布情况。当sp>1时,三角形向中间聚拢;当sp<1时,三角形向两边聚拢。图4所示为sp=2时隶属度函数的形状。
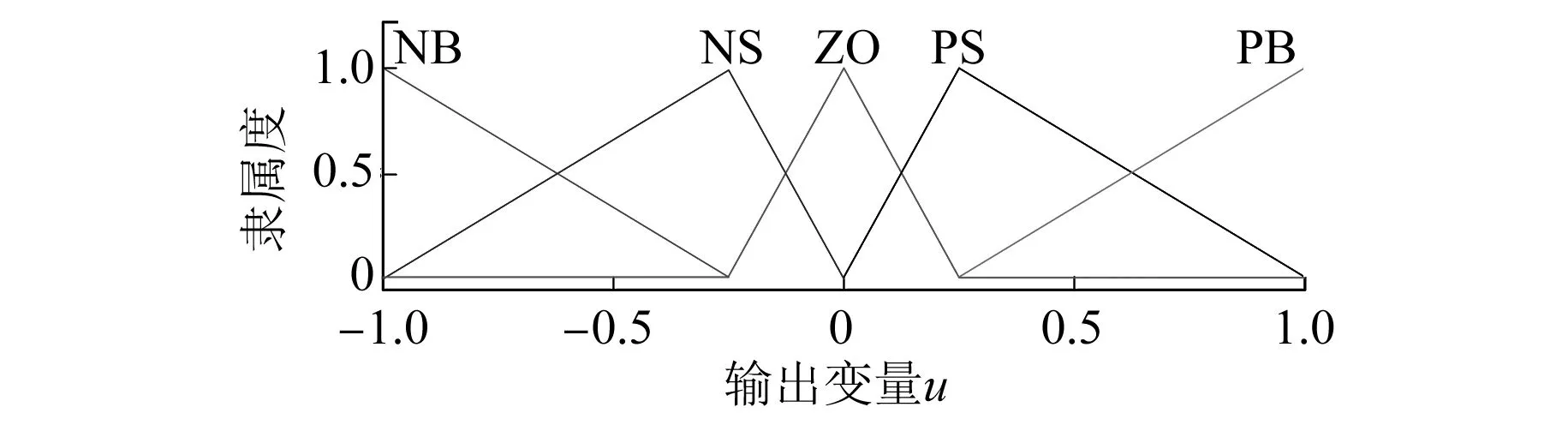
图4 间隔参数为2时的隶属度函数
作为输入量,误差和误差变化率的量化因子分别为ke和kec,电机的转速作为输出其比例因子设定为ku。综合考虑电机控制的精度和响应速度,e和ec均选择了5个模糊子集(NB、NS、ZO、PS、PB),控制量u选择了7个模糊子集(增加了NM-负中和PM-正中2个子集)来覆盖论域。
2.2.2 知识库和模糊推理
知识库当中存放的是各个输入和输出量在进行模糊化时设定的论域映射关系,以及设定的模糊子集个数。知识库当中还应当建立语言规则库,用来设定输入输出之间的关系,从而反映出控制规则。这些规则的制定是通过人的经验和直觉用相应的语言描述出来的[9]。模糊控制规则如表1所示。该控制系统一共有25条模糊规则。
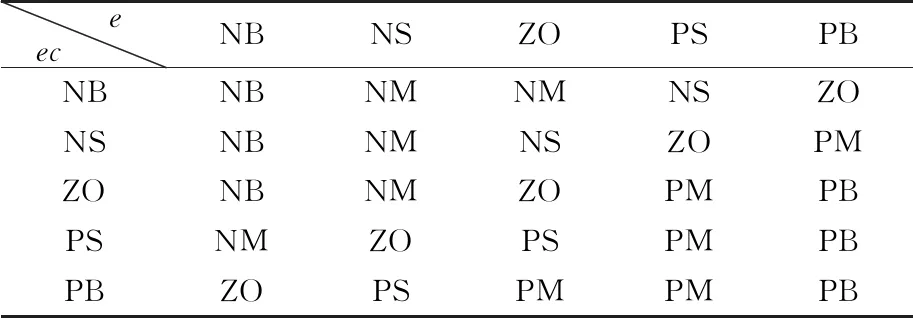
表1 模糊控制规则状态
2.2.3 精确化计算
模糊量需要转换为精确量才可以对系统进行控制。本文运用重心法将模糊量转变成精确量,该方法将面积的重心作为推理结果。运用重心法解模糊的过程类似于加权平均法,其权值为各元素的隶属度[10]。其计算式如下:
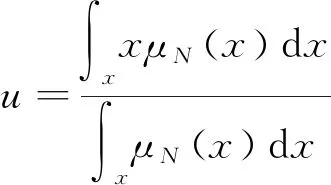
(1)
3 ASAPSO算法
3.1 模拟退火算法
模拟退火算法是受固体退火的原理启发而形成的[11]。固体加温的过程中,由于其内部粒子运动速度加快,内能不断增大,当其达到一定的温度后开始降温,内部粒子由快速运动逐渐减慢,内能也逐步减小,粒子趋于稳定,最后在固体温度达到稳定值常温时,内能保持在稳定状态即最小值。
其基本思想是:目标函数f的设定遵循的原则为寻求固体内能E的最小值,其中E为固体在温度为T时的内能,不同T时内能的改变量为ΔE。算法由初始解i和温度T演化的控制参数t开始,对当前解重复进行“生成新解—算目标函数差值—判断是否接受”的迭代,t值不断衰减,并在终了时得到近似的最优解。退火进程包含了给定初始温度T开始、每个t值时刻的迭代次数k和停止条件S[12]。
基本流程:
(1) 给定初始温度T开始(T充分大)及初始解状态,每个t设定的迭代次数k,最低温度T终止;
(2) 计算该点的适应值E=f(S);
(3) 更新计算当前温度t;
(4) 产生新解S′;
(5) 计算新解的适应值E′=f(S′)以及适应值增量ΔE=f(S′)-f(S),如果满足终止条件则停止算法。
3.2 ASAPSO算法优化模糊控制器原理
与标准PSO相比,自适应模拟退火粒子群算法在算法优化过程中能够根据各个粒子的适应值主动调节学习因子,从而克服了局部收敛的问题[13]。在前一阶段利用标准PSO算法寻求优化,以提高算法的运行速度,后一阶段结合模拟退火算法,不断优化更新参数并寻求最优解。
为了提高PSO算法解决全局优化问题的能力,鉴于ASAPSO 算法的寻优特点和能力,在对模糊控制器4个参数的优化上,运用ASAPSO算法对其进行优化。图5所示为ASAPSO算法对参数寻优的原理图。
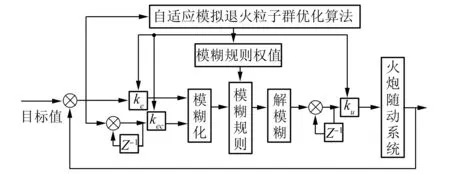
图5 ASAPSO算法对模糊控制器的参数寻优原理图
寻优参数为模糊控制器输入参数量化因子ke和kec、输出参数比例因子ku以及模糊规则权值[14]。其中ke和ku取值范围设定为 1~10,kec和模糊规则权值取值范围为 0~1[15]。适应度函数如下:
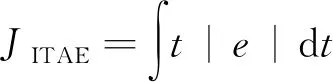
(2)
算法的流程图如图6所示。
4 仿真分析
4.1 仿真模型
基于MATLAB/Simulink建立的火炮随动跟踪系统控制模块和执行机构仿真模型如图7所示[16]。
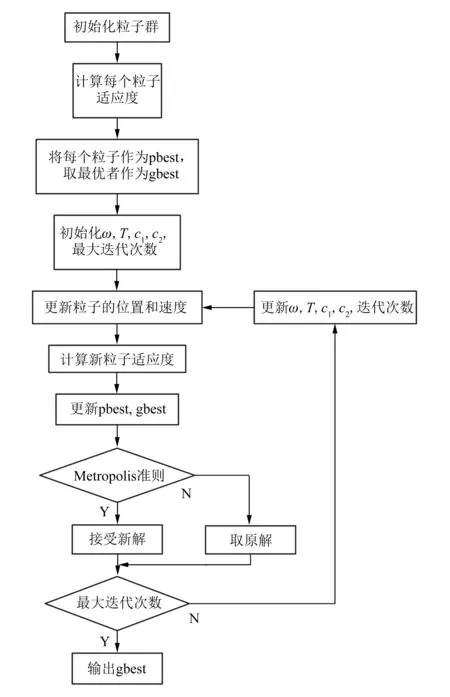
图6 ASAPSO算法对模糊控制器的参数寻优流程图
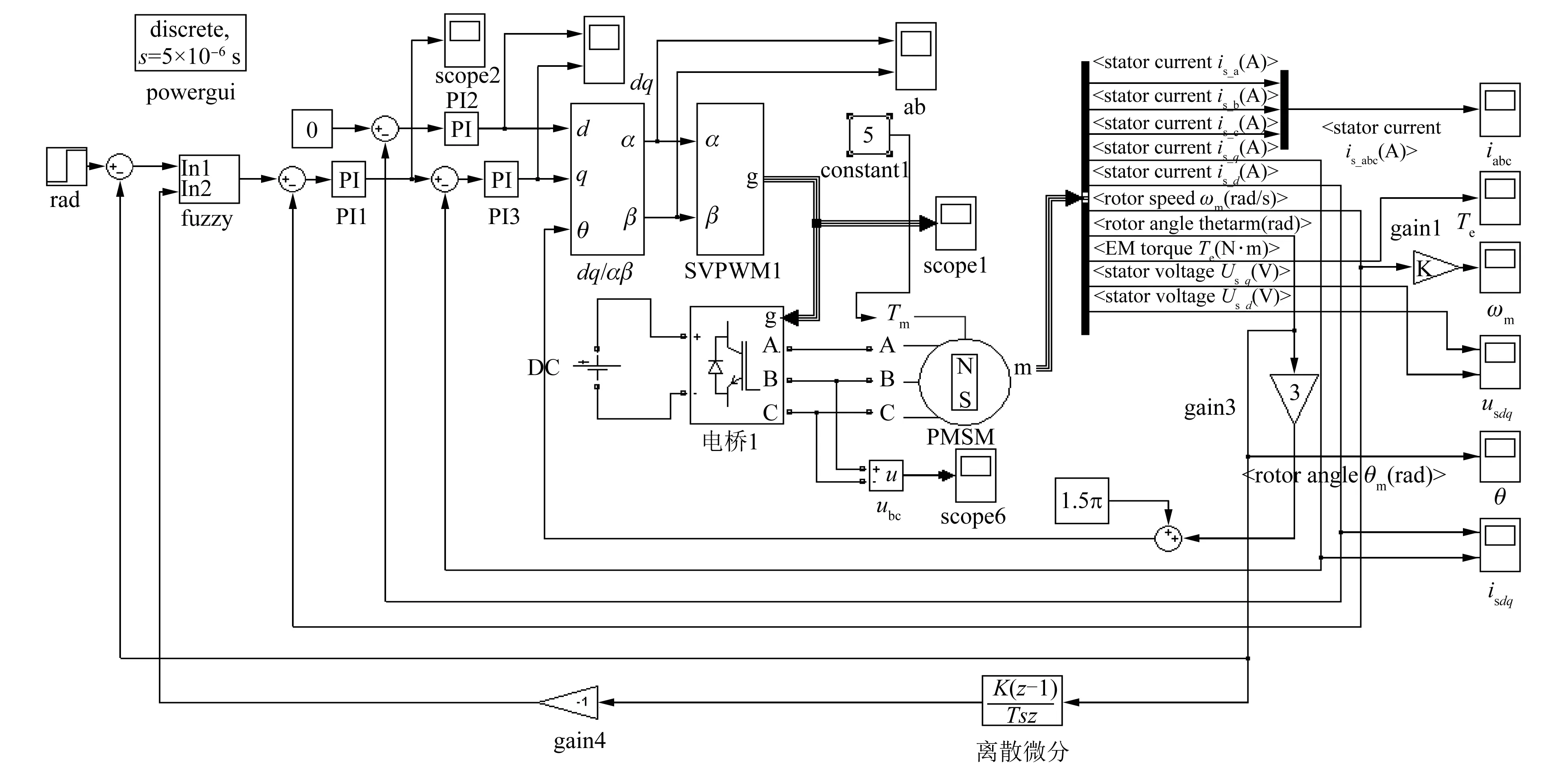
图7 基于ASAPSO的火炮随动系统模糊控制仿真模型
4.2 结果分析
PMSM的参数为:电阻R=3.8 Ω,电感L=8.7 mH,永磁磁链0.185 Wb,转动惯量J=1 kg·m2,摩擦系数f=0.398 2×10-3N·m·s,负载转矩5 N·m,极对数n=3,母线电压值300 V。
将PD控制器加入系统位置环,设定p=6,d=0.3,设置仿真时间0.4 s,给定目标位置角度值设定为阶跃信号。获得的位置响应曲线如图8和图9实线所示。
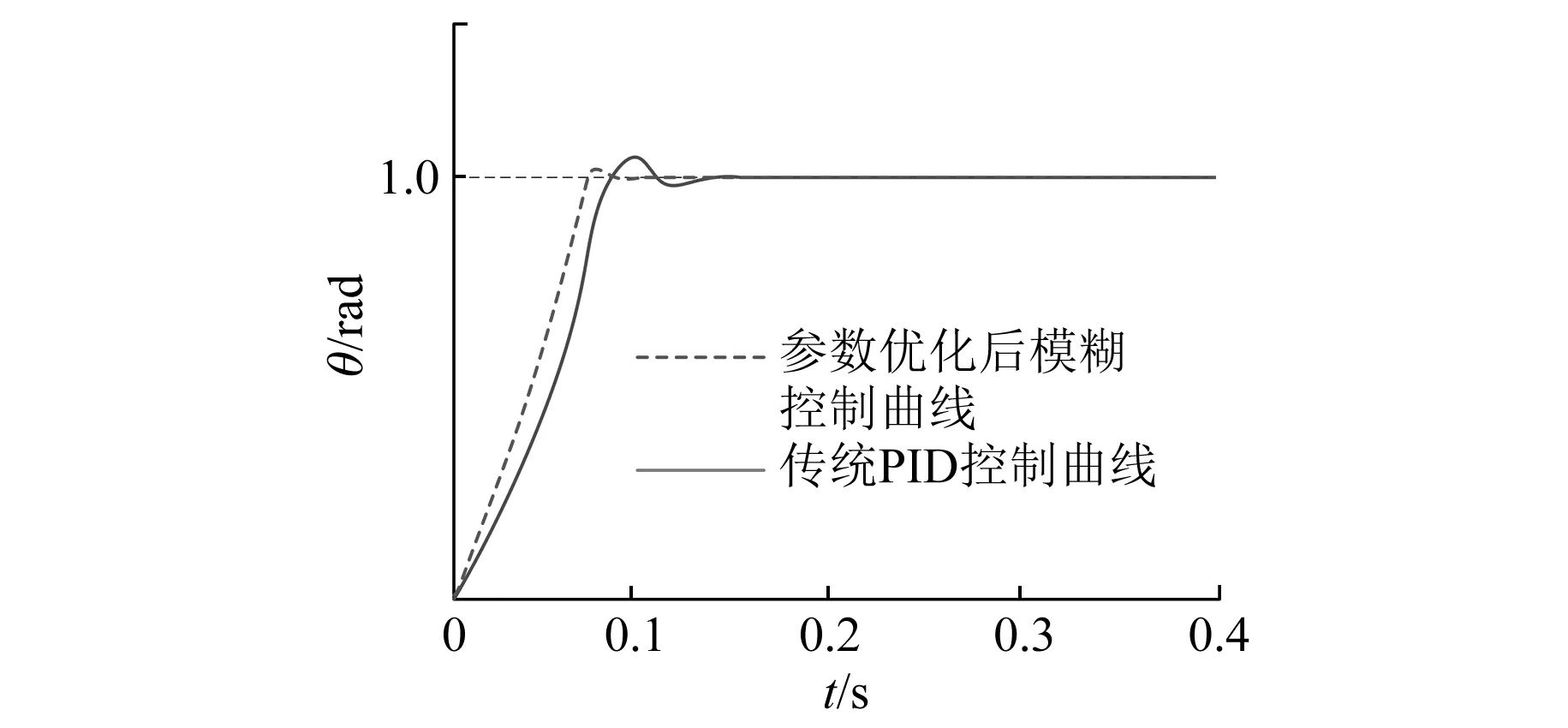
图8 对比两种控制器获得的位置响应仿真波形
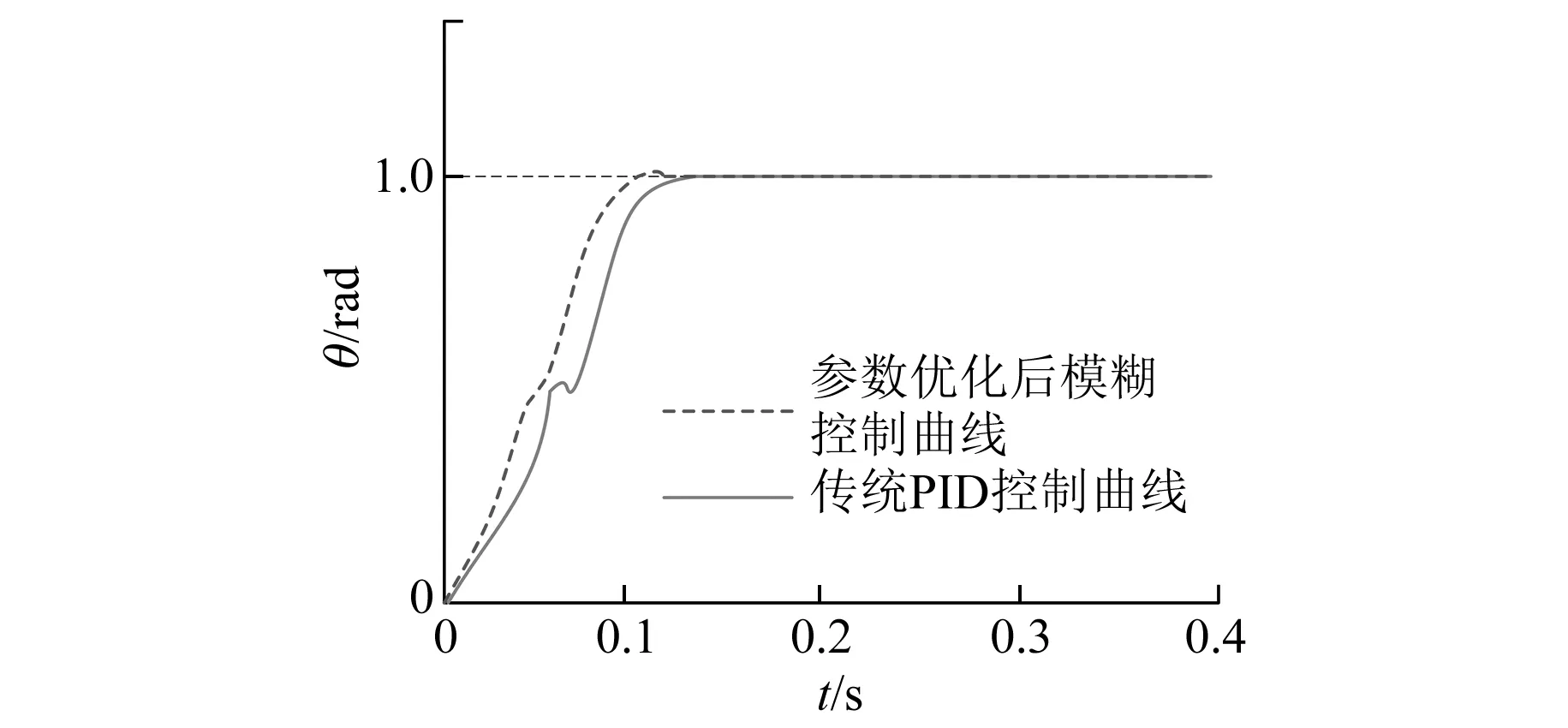
图9 转矩扰动对两种控制器位置响应曲线的影响
量化比例因子分别为ke=5.08,kec=0.12,ku=4.83。将数据代入模糊控制器,替代PD控制器,用图7所示的仿真框图进行仿真试验,仿真结果如图8和图9虚线所示。
图8所示为传统PID控制器和参数优化后的模糊控制器获得的位置响应曲线。图9所示为转矩扰动对2种控制器位置响应曲线的影响。
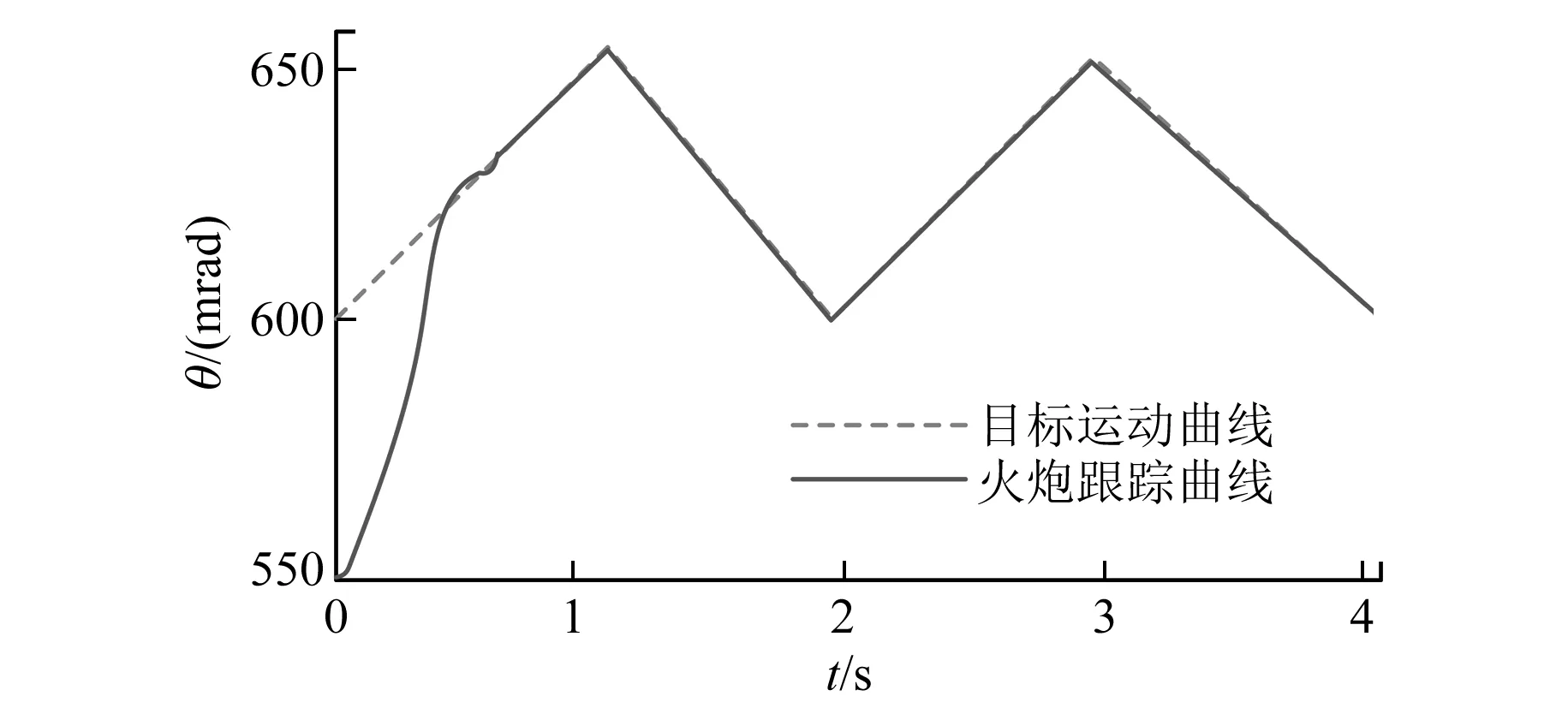
图10 参数优化后模糊控制器的跟踪响应曲线
分析仿真结果可知:参数优化后,模糊控制器的各项性能明显优于传统PID控制器,当给定角度随时间发生变化时,模糊控制器能够更快速稳定地响应,且超调量明显小于PID控制器。图9显示出了2种控制方式在转矩扰动时的控制曲线,从图9可以看出转矩扰动对模糊控制器影响较小。
图10所示为系统的跟踪性能曲线。根据图10的仿真曲线分析,跟踪响应模拟目标运动最大角速度55 mrad/s,目标起始位置600 mrad,火炮身管起始位置0。通过仿真发现,参数优化后的模糊控制器能够快速响应,具有良好的跟踪性能。
5 结 语
本文以改进某型地面火炮随动控制系统跟踪性能为出发点,提出了以PMSM替代传统直流电机作为火炮随动系统高低和方向的执行元件,并在此基础上研究了火炮随动系统的位置环控制策略。通过MATLAB仿真,对比了传统PID控制和经优化参数之后的模糊控制器作为位置控制器的响应曲线。
结果表明,自适应模拟退火粒子群优化算法的优化效果显著,控制效果较好,系统的静态特性和动态特性比传统PID控制更好,能够有效克服转矩扰动等非线性因素的影响,系统具有较好的目标跟踪性能。

