扇形静压转台结构设计与仿真分析

王永柱，戴惠良，冯星鑫，韩凯凯

（1.东华大学机械工程学院，上海201620；2.上海航天控制技术研究所，上海201109）

1 引言

液体静压支承技术是把油垫支承的作用应用在机床导轨的技术，由于具有承载力、油膜刚度高和摩擦系数低等优点，广泛应用在重载、高精密的数控机床等设备中。由于静压油腔支承性能会影响承载能力和加工精度，为保证静压油垫的承载力和油膜刚度符合使用要求，要对静压油腔结构和油腔中流体流动的机理进行深入研究[1]。文献[2]利用流体动力学软件FLUENT 研究了静压轴承内部压力场、温度场的分布，并分析了承载力与偏心率的关系。文献[3]分别模拟了矩形、扇形、椭圆形和工字型油腔中油膜的压力场，得到承载力由大到小分别为椭圆形、扇形、矩形、工字型的结论。文献[4]利用MATLAB 软件对高精度动静压油膜轴承的油膜性能进行了数值解算，实现了压力场的三维仿真。文献[5]以闭式静压导轨为对象，基于力平衡方程和流量方程，建立了功率损失、静态性能、动态性能的数学模型，研究了油膜厚度对静压支承的影响，得到了减小油膜厚度可以降低导轨总功率损失、提高静态性能和动态性能的结论。

2 闭式静压支承原理

闭式静压导轨依靠一定的几何结构使运动件只能沿运动方向移动，结构复杂，但能承受多方向的载荷，油膜刚度大，受偏载和抗倾覆力矩能力强。受到压力的液压油通过节流器后进入导轨开设的上下油腔内，如图1 所示。导轨受到向下的作用力使油膜厚度减小Δh。即导致上油腔因间隙变大而使封油边液阻减小，而此时上油腔的节流器输出流量不变，从而使上油腔内压力减小；下油腔由于载荷F使油膜厚度减小Δh，封油边液阻的增加使油腔中的压力变大，而此时节流器输入流量仍不变，从而产生更大的压力支承动导轨，上下导轨压力此消彼长之下，使动导轨处于平衡位置。

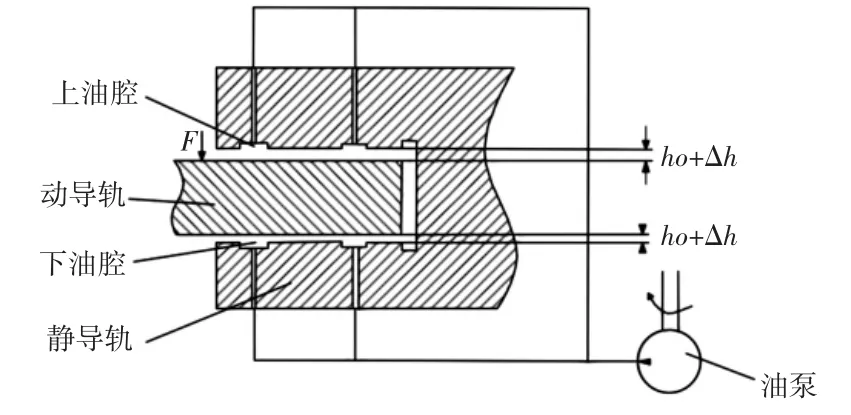
图1 闭式液体静压支承原理Fig.1 Schematic of Closed Hydrostatic Support

3 数控磨床及转台参数要求

平面二次包络环面蜗杆数控磨床对转台要求主要体现在转动精度、油膜刚度、转台转速以及承载能力等参数方面，在磨床设计中，转台所承重部件为工作台、磨头及立柱，初步确定转台参数[6]，如表1 所示。

表1 数控磨床参数Tab.1 CNC Grinding Machine Requirements Parameters

3.1 受力分析

平面二次包络环面蜗杆数控磨床中，由于砂轮、法轮盘和电机等部件在立柱内，立柱用螺栓固定在转台的工作台上，当转台静止时，转台受到立柱部分重力G1和工作台的重力G2之和W1。

当加工时，砂轮的表面有大量磨粒参与到磨削过程中，将产生的磨削力分为三个方向的分力：轴向磨削力Ff、法向磨削力Fp和切向磨削力Fc。

3.2 油膜承载能力

承载能力是指一定油膜厚度下所能承受载荷的能力，通常导轨上的载荷具有一定的变动范围，毛细管节流不等面积对置油垫的承载能力为[7]：

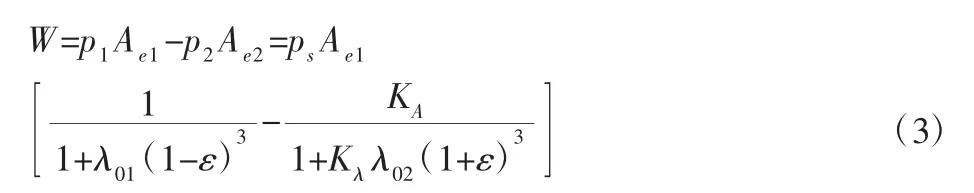
式中：Ae1、Ae2—上下油垫的有效承载面积；λ—油垫在设计状态下的液阻比；ε—油膜位移率；KA—上油垫与下油垫的有效面积之比；Kλ—上油垫与下油垫结构参数之比。

当Kλ=1 时，由公式（3）得到承载能力和位移率、面积比之间的关系，如图2 所示。由图3 可知，当面积比一定时，转台承载力大小随位移率增大而提高；当油膜位移率一定时，转台承载力随面积比增大而减小。

图2 承载能力与位移率关系Fig.2 Relation Between Carrying Capacity and Displacement Ratio and Area Ratio

3.3 油膜刚度

油膜刚度即在外力作用下油膜抵抗外载荷所需要的载荷变动量，对置油垫在主油垫间隙为h1时的油膜刚度为[8]：

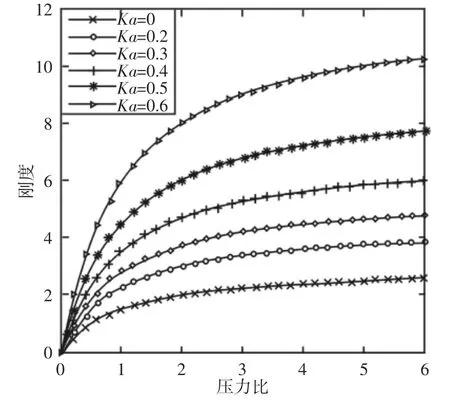
图3 刚度与压力比和面积比关系Fig.3 Relation of Stiffness between Pressure Ratio and Area Ratio

当ps、Ae1和h0为确定值时，由式（5）得到刚度S与压力比λ0和面积比KA关系，如图3 所示。

由图3 可见，当设计载荷和间隙为一定时，刚度随压力比和面积比的增大而提高。对于不等面积对置油垫，通过增大面积比的值提高刚度比增大压力比更为有效。

根据图2 和图3，结合刚度和承载力的综合关系，选择面积比KA=0.6。

3.4 确定油垫尺寸

根据磨床总体结构可以确定扇形液体静压转台远端油垫半径为：R1=600mm，R3=500mm，主导轨径向封油边的宽度取0.25（R1-R3）=25mm，则R2=575mm，R4=525mm，径向回油槽宽10mm，如图4 所示。

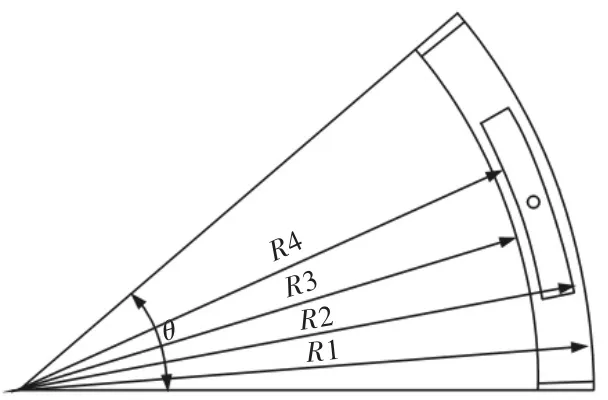
图4 扇形油垫不同半径Fig.4 Different Radius in Fan-Shaped Oil Pad

由于转台径向半径远大于油腔宽度，可将扇形油垫近似折合成矩形油垫，其尺寸为：

封油边长度越长会出油腔内产生的压强和承载力越高[1]，取封油边为100mm，则l1=147mm。

主油垫的有效承载面积为：

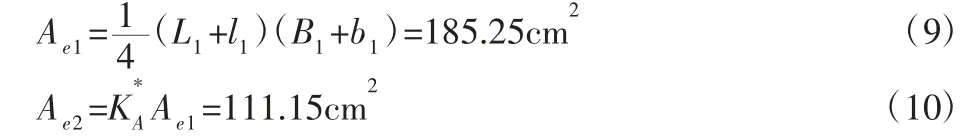
3.5 确定进油压力

在设计载荷W0的作用下，动导轨处于对置油垫的中间位置，由公式：

4 静压转台结构设计

传统环面蜗杆数控磨床加工工件时，由于砂轮的切削点距离回转工作台回转中心的距离过大，导致蜗杆齿面出现形位超差、磨削精度不够等问题，为解决这一问题，设计扇形液体静压回转工作台，磨头及立柱部分利用T型块安装在扇形工作台上，保证转台的回转中心与砂轮中心点在同一竖直位置，由此既避免了转台与工件台的干涉，又减小了对转台回转精度的要求，提高了加工精度。

静压转台截面图，如图5 所示。转台由底座、工作台、导向块、动导轨、节流器等部分组成，工作台与动导轨、导向块与底座之间由螺栓连接固定，节流器安装在工作台面下，在工作台内开有油孔，液压油由节流器通入油孔进入动导轨的上下油腔，油泵供给油液足够压力以支承起工作台及工作载荷，并保持稳定，液压油沿开设在导轨上的回油槽进入出油口流回油箱，经过滤后可循环使用。扇形转台三维模型，如图6 所示。

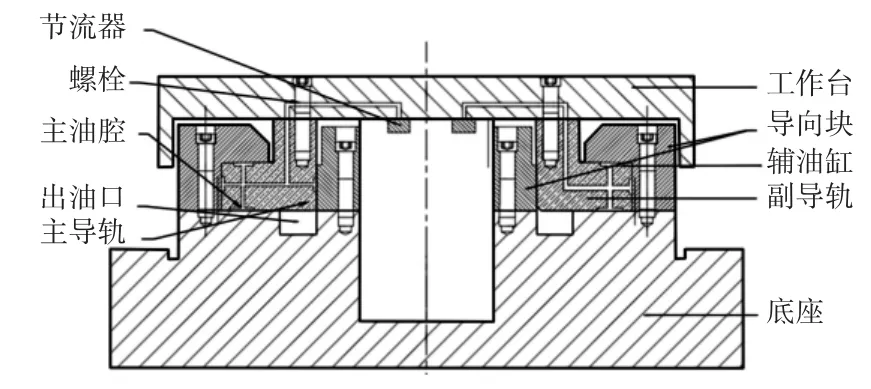
图5 液体静压转台截面图Fig.5 Cross Section of Hydrostatic Table

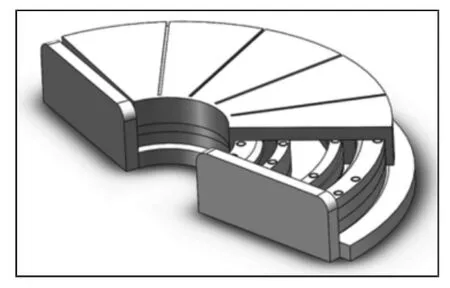
图6 扇形液体静压转台三维模型Fig.6 Three-Dimensional Model of Fan-Shaped Hydrostatic Table

5 静压导轨油膜流体仿真模拟

5.1 假设条件

在对静压油腔内部流体数学建模之前，需要对其提出一定假设条件[9]：

（1）假设在静压油腔内部流场内，流体为不可压缩流体并且其流态为三维定常流动；

（2）润滑油与固体之间无相对滑动；

（3）润滑油的惯性力忽略不计且油膜出口边界压力为零；

（4）润滑油由进油口进入导轨内部，经计算其雷诺数小于2300，可以视为层流，

（5）在工作台转动时，不考虑工作台及底座的热变形。

5.2 FLUENT 计算及分析

设计中的扇形多油腔转台是由六个对置油垫负责支承，考虑其结构对称性特点，选择主导轨中的一个油垫进行模拟分析。油膜模型由三个部分组成：进油管、扇形油腔和油膜薄层，其中油膜薄层两侧为油液出口。

模型的网格划分采用ANSYS ICEM 软件，由于油膜薄层厚度极小，为了获得高质量网格利用拓扑分块进行模型的拓扑构建，将油膜薄层处划分为5 层网格，进油管处为获得高质量网格，采用O型网格切分[10]，并将梯度较大区域的网格细化，然后将拓扑得到的结构网格转化为非结构网格。

边界类型设置为：pressure-inlet、pressure-outlet、wall，计算区域类型为FLUID。计算过程中，流场中流体视为不可压缩流体的三维定常流动。

对于两种不同油腔结构，液压油静态压力分布都呈现为由进油口向出口分阶减小，在矩形油腔内部压力最大且保持恒定状态，在油腔与油膜层交界处压力变化较大，至出口处逐步线性减小至标准大气压，如图7、图8 所示。通过在Fluent 的后处理中对油膜下表面进行压力积分，得到工字型油膜承载力为11612N，口字型油膜承载力为12642N，口字型承载能力相对较高[11]。

图7 口字型油腔压力分布云图Fig.7 Pressure Distribution Cloud Map of Square-Type

图8 工字型油腔压力分布云图Fig.8 Pressure Distribution Vector of H-Type Oil Cavity

两种结构油腔内部的流速分布矢量图，如图9、图10 所示。口字型油腔中在进油口左右两侧流场存在对称分布的涡旋流场，由进油口处向油腔四壁流动，由于油腔四个内壁阻隔而产生回流流场，由图9 可以看出油腔内部液压油在左上部和右下部流速最高，左右两涡旋流场的对称性使油腔内部承载力分布较均匀，且不易产生倾覆。

图9 口字型油腔流速分布矢量图Fig.9 Velocity Distribution Vector of Square-Type Oil Cavity

图10 工字型油腔流速分布矢量图Fig.10 Velocity Distribution Vector of H-Type Oil Cavity

工字型油腔中由于进油口的周围被墙壁阻隔，液压油在流通域内流速变化大且产生多个涡旋，涡旋流体之间剪切力作用产生热量易造成导轨面的热变形，且从图10 可以看出此结油腔结构中左下部存在流速最高点，油腔内部流速差别较大，不利于保持油膜的刚度性能。

6 刚度实验验证

对油垫的静刚度进行检测，验证其是否符合设计要求。通过数字式电感测微仪获得油膜受力而产生的微小位移，利用油垫刚度为油垫受到载荷后发生的与位移成正比的比例关系来获得油垫刚度值[12]。

测试方法：

（1）把测微仪的底座固定在转台水平面。

（2）把测微仪的电感触头安装在动导轨一侧。

（3）调节测微仪触头与转台平面的接触位置，使显示读数在可读范围之内。

（4）恢复默认设置，记录初始值并记为零点。

（5）在转台上施加垂直方向上不同数值的力，分别记录下测微仪显示的数值。

（6）对数据在MATLAB 上处理，获得图像。

搭建的转台直位移测量装置，如图11 所示。施加载荷与油膜位移量关系图，如图12 所示。

图11 转台垂直位移测量装置Fig.11 Rotary Table Vertical Displacement Measuring Device

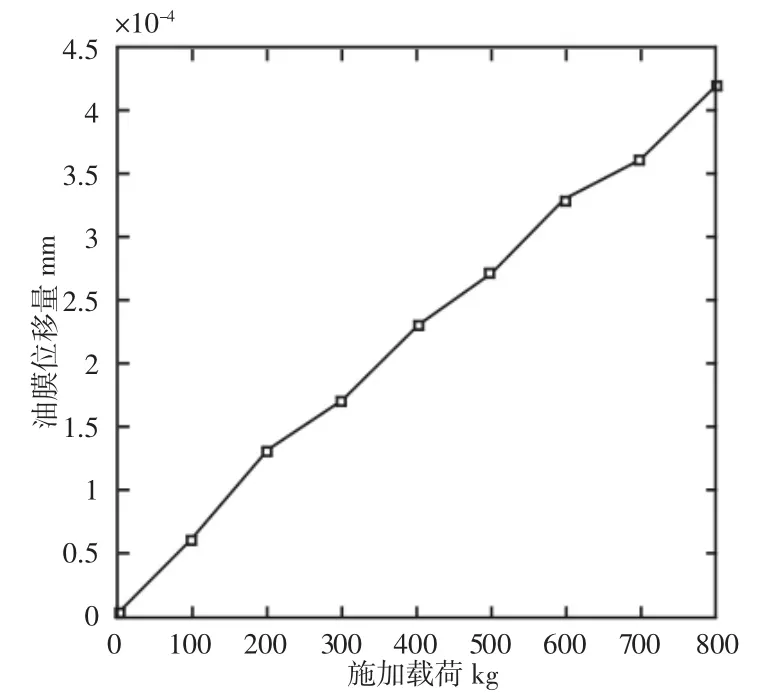
图12 施加载荷与油膜位移量关系图Fig.12 The Relationship Between Loading and Displacement of Oil Film

通过对测量得到的数据将施加载荷与位移量在MATLAB中作出坐标图，通过图12 可以计算到油膜的竖直刚度大约为200N·μm-1，与理论仿真所计算得到的刚度比较符合。

7 结论

（1）针对平面二次包络环面蜗杆数控磨床的结构参数和工况，对扇形静压转台受力分析，建立了油膜承载力和油膜刚度的数学模型，通过理论分析得到：承载能随着面积比的增大而减小，随着位移率的增大而增大、刚度随着压力比和面积比的增大而提高，利用其关系曲线可选取面积比最佳值为（0.5～0.7），提高转台油腔结构设计选择的效率。（2）对矩形油垫的上壁面压强积分得到在垂直方向的支承力为12642N，证明了根据理论计算结果选择油腔尺寸参数符合磨床工作要求。（3）对口字型油腔结构和工字型油腔结构进行流场分析，得到压力分布和流场速度分布，口字型油腔的速度波动范围工字型油腔相对口字型油腔的速度波动大了1.37 倍，证实油腔中没有内壁阻隔承载能力相对更为均衡，且更有利于油垫的整体稳定性。