基于Recurdyn 的某无人平台悬架系统优化设计

吴 天，任志英，刘 岩，郑文彬

（1.福州大学机械工程学院，福建 福州 350000；2.新乡北方车辆仪表有限公司，河南 新乡 453000）

1 引言

无人平台系指无人驾驶的、完全由遥控操作或者按预编程序自主运作的平台。就目前而言，大致包括为无人作战平台与无人运输平台。因无人平台在设计时无需考虑人的因素及其相关的设备，成本低廉，全寿命费用大为减少。无人平台是近几年新出现的概念，国外提出发展无人平台都是有明确的需求背景的，如考虑到未来局部战争等环境十分严峻的战场，各种高新技术武器装备充斥在其中，命中精度高、机动性强、射程远、杀伤威力大等，这对交战双方都构成极大的威胁。如何以最小的损失以及人员伤亡取得最大的战果，这是各国军事作战部门优先关注的问题。此外，各国在发展新武器装备时都面临着预算日趋拮据而装备费用日趋上涨的困境，如何谋求经济上能负担得起的高效费比武器装备也成为各国优先考虑的需要。除此之外抢险救灾上无人平台也可提供强有力的支援，减少人力消耗以及事故中人员伤亡。

底盘悬架对于无人平台是极为重要的组成部分，它具有承载、传力（矩）、缓冲、衰振、散能以及调节平台高度等主要功能，对保护平台中的精密仪器有巨大作用。而悬架空间结构复杂，传统设计分析方法难度大，效率低，通过改变悬架设计硬点参数是一种优化悬架特性的有效方法，但是如果考虑多个定位参数之间的相互影响，通过大量设计参数相互权衡得到理想的特性十分困难，因此悬架的设计是一个复杂的多目标优化问题[1]。Recurdyn/AutoDesign 模块是一个集DOE、元模型（MetaModel）技术和数值优化技术为一体的自动化设计优化工具，几乎采用最小的采样点构建初始元模型，在优化过程中，通过自动地提高元模型的保真度，克服了由于数据不足而引起的数值奇异，从而避免了优化过程的分析失败[2]。基于Recurdyn 对双横臂式悬挂系统进行建模和仿真，分析评价其性能，再对悬架定位参数进行优化，对于悬架设计具有一定指导作用。

2 无人平台以及悬架模型

此次选择的是一吨级6×6 多功能无人平台，采用全电动底盘，六电机分布式驱动，具备全地形通过、多模式人机交互、高可靠通信等性能，可实现目标潜伏侦察、阵地全景观测、物资自主运输等。其中平台质量800kg，载重质量400kg，最大速度30km/h，无人平台实物，如图1 所示。

无人平台在执行特殊任务时所搭载的任务单元需要减振缓冲，且通过性能要好，因此平台对于悬架有较高的要求。综上考虑多方面因素，选择双横臂式悬架，双横臂式独立悬架拥有横向刚度大、抗侧倾性能优异、抓地性能好等特性。按上下横臂是否等长，可分为等长双横臂式和不等长双横臂式两种悬架。等长双横臂式悬架在车轮上下跳动时，能保持主销倾角不变，但轮距变化大，造成轮胎磨损严重，现已很少用。对于不等长双横臂式悬架，只要适当选择、优化上下横臂的长度，并通过合理的布置、就可以使轮距及前轮定位参数变化均在可接受的限定范围内，保证平台具有良好的运动稳定性，从而保护所搭载的任务单元。典型的双横臂悬架系统由5 个部分组成：上摆臂、下摆臂、拉杆、转向节、阻尼减震器和轮胎。上下摆臂为非等长结构，通过转动副与车架相连接，转向节通过球铰与上下摆臂以及转向横拉杆连接，转向横拉杆再与车架通过球铰连接[3]，如图2 所示。

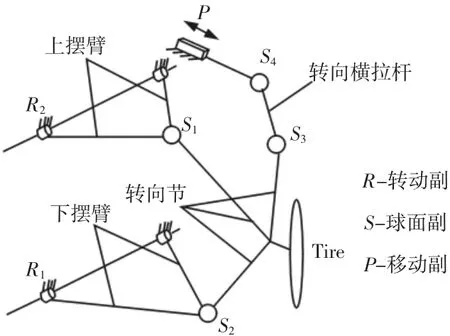
图2 双横臂悬架简图Fig.2 Sketch of Double Wishbone Suspension

双横臂悬架系统模型的自由度F=5×6－4×3－2×5－1×6=2，即车轮绕主销的旋转和车轮垂直跳动两个自由度。硬点的空间位置坐标是建立运动模型的关键，首先在Solidworks 中使用测量工具测量关键硬点的参数，而后在Recurdyn 中建立参数点、设计变量，参数点位置，如图3 所示。A、B、C点分别为下摆臂前、后、外支点；E、F、D分别为上摆臂前、后、外支点，G、H分别为转向横拉杆外、内支点。悬架实物，如图4 所示。

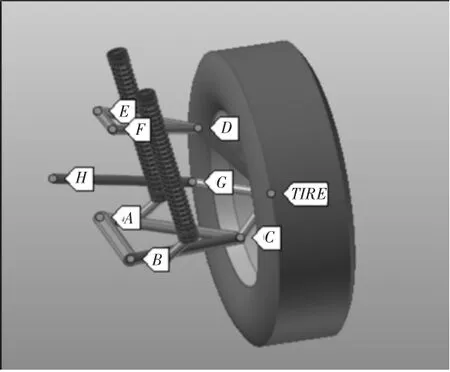
图3 Recurdyn 后悬架仿真模型Fig.3 Rear Suspension Simulation Model in Recurdyn

图4 悬架Fig.4 Suspension

3 设计优化

3.1 设计变量选择

表1 设计变量参数Tab.1 Parameters of Design Variables

综上所知，所选硬点共8 个，以各个硬点的X、Y、Z三个坐标作为设计变量，共得到24 个设计变量，如表1 所示。表1 所提供的坐标数据已坐标变换，下摆臂AB中点为坐标原点[4]。

3.2 目标函数设计

目标函数是为了找出满足其功能性或其他要求的可接受的设计，满足整个设计约束的可接受设计称为可行性设计，优化中会有多个可接受设计，为了找出最优方案，必须通过一个准则进行判别优劣，该准则一般表示为设计变量的函数[5]。此次优化为多目标优化，因为选择的无人平台属于低速平台，转向方式为差速中心转向，且各点变化范围很小，对主销内倾角与主销后倾角影响不会太大，故暂不考虑主销内倾角与主销后倾角，只考虑前束角与轮胎外倾角。我们目的是减小前束角和外倾角振动范围。Recurdyn 不能直接提供这些值，因此要通过使用表达式（Expression）和变量方程（Variable Equation）来进行计算，为此，可以先得到前束角和外倾角的最小值和最大值。这样，最大值与最小值之间的差值就是其振动范围，则优化问题就是要减小前束角（AR1）和外倾角（AR2）在轮胎跳动时的振动幅值。

3.3 设计指标制定

确定目标函数后，设置约束条件，范围要小于优化前的值，默认权重比为1，如图5 所示。设计问题定义为MinF1和MinF2，约束条件为R1≤C1，R2≤C2，因为目标优化的质量取决于初始样本的数量，而这里的问题有24 个设计变量，这需要非常多的采样点，但这两个不等式约束可以避免未成熟收敛。则设计指标的计算方法为：

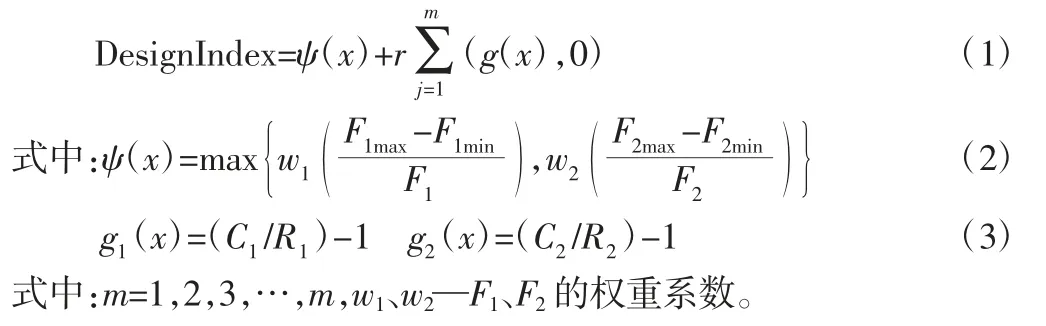
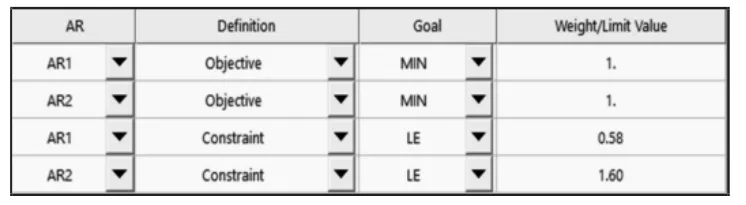
图5 目标函数约束设置Fig.5 Setting of Objective Function Constraint

3.4 DOE 分析

设计研究的主要目的是分析各个设计变量的变化对系统性能的影响、设计变量的最佳取值以及系统性能对设计变量变化的敏感程度。DOE 是安排试验和分析试验数据的数理统计方法，主要是进行合理的安排试验，用很小的试验规模、较短的周期以及较低的试验成本，通过试验设计，能够考虑再多个设计变量同时发生变化时，各个变量对系统目标性能的影响[6]。基于Recurdyn软件环境的设计研究包含了灵敏度分析及设计变量筛选，提供多种试验设计方法，如三水平正交设计等[7]。由于选择变量的个数是24，如果选择3-Level Orthogonal Array 需要进行52 次试验，为减少试验次数，选择2-Level Orthogonal Array，只需要32 次试验，且优化结果相差较小。各个变量分别对目标函数1（前束角变化）与目标函数2（外倾角变化）的敏感程度，如图6 所示。

图6 设计变量DOE 分析图Fig.6 DOE Diagram of Design Variables

由图可知，右边位置的点比左边的点更加敏感，对于目标函数1 设置的截止值（Cutoff Value）是0.26，目标函数2 设置为0.2，最后筛选出的设计变量共12 个，如图7 所示。大多数的有效设计参数是Z轴的值。在Recurdyn 中用于元模型的DOE 方法有FC中心复合设计（CCD）、经典二次响应面模型法（BBD）等5 种，元模型的初始DOE 选择方法，如图8 所示。当前设计在中心位置的50%范围内，建议使用ISCD-1 或ISCD-2，并且此方法还能缩小取样数，其中，ISCD-2 一般用于设计优化，ISCD-1 用于DFSS/稳健设计优化。由此可得此次设计选择的初始DOE 法为ISCD-2（Incomplete Small Composite Design-ll），如图9 所示。

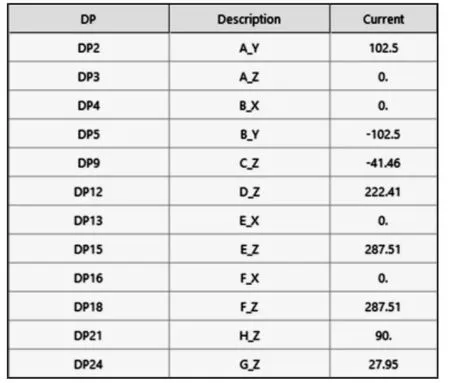
图7 筛选出的设计变量Fig.7 Screened Design Variables

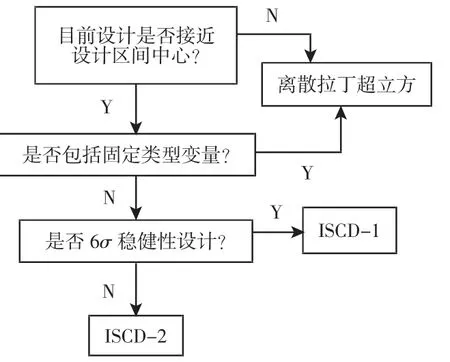
图8 DOE 选择方法Fig.8 The Selection of DOE Method

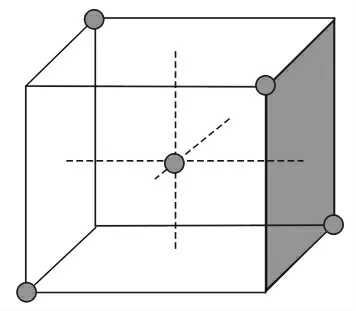
图9 ISCD-2Fig.9 Incomplete Small Composite Design-ll

3.5 元模型（Meta-Model）方法选择

Recurdyn 的元模型方法包括了协同克拉格法、径向基函数法、保守响应面法以及多项式函数法，选择方法，如图10 所示。综上可得，元模型方法选择MQ 径向基函数法。径向基函数（RBF）是用于插值目的的一类函数，其处理多元函数逼近问题具有效率高，运算简单，不依赖于网格，求解精度高等优点。它们的值只取决于一般点和特定函数中心之间的距离[8]。RBF 法利用径向基函数Bi（x）和多项式基函数Xj（x）构造了逼近所有采样点的近似函数y（x）[9]。近似函数y（x）的描述如下：

由于距离是标量值，矩阵B是对称矩阵，因此，如果矩阵B的逆存在，则保证了唯一解[10]。

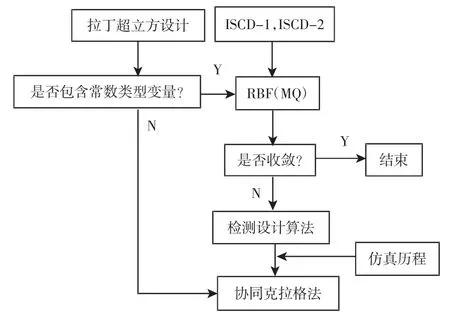
图10 元模型的选择方法Fig.10 The Selection of Meta-Model Method

4 优化结果分析

4.1 优化结果

优化结束后，可得到收敛历程以及优化结果，如图11 所示。优化过程仅在第16 个迭代步便收敛。整个优化过程共32 次计算，包括17 次初始采样点分析。优化后各点取值，如表2 所示。两个响应目标AR1 和AR2 在最优解时取值分别为0.14、0.52，如表3 所示。

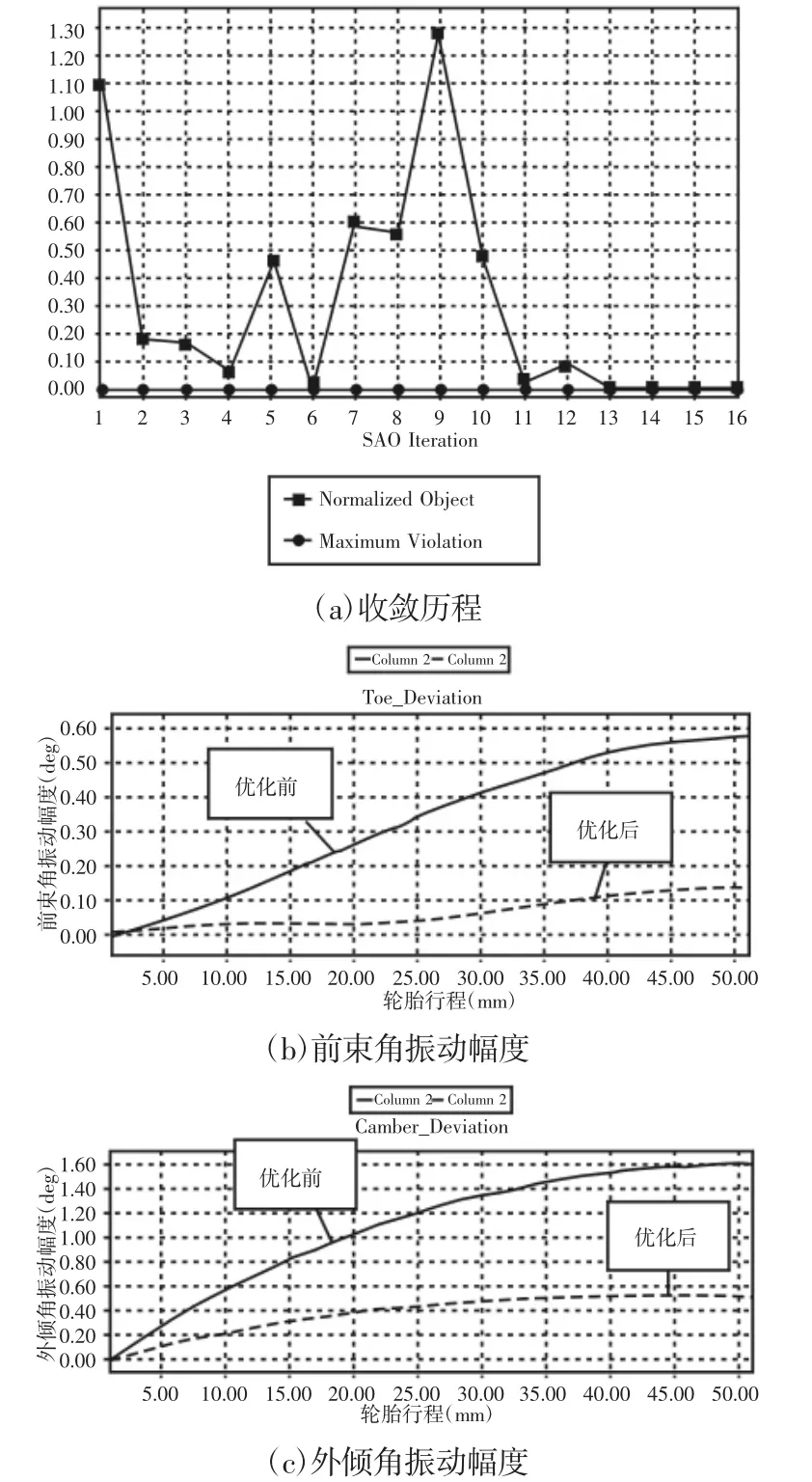
图11 优化结果Fig.11 Optimization Results

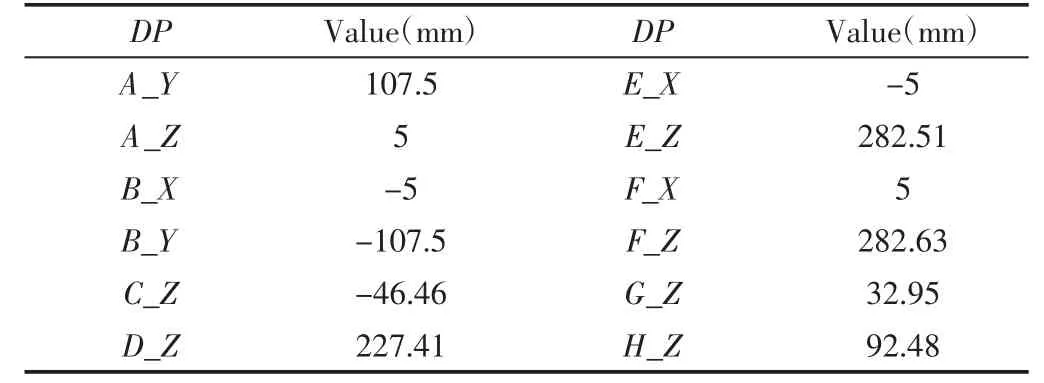
表2 优化后定位参数取值Tab.2 Values of Parameters After Optimization

表3 定位参数优化结果Tab.3 Parameter Optimization Results

4.2 结果分析

由以上结果可知，优化后的数据与优化前的0.58、1.60 相比减少很多，表明在优化后各个车轮在垂直跳动时前束角与外倾角变化数值更小，运动也更加平稳。变化范围，如表4 所示。在车轮的整个跳动范围内。优化后的无人平台过0.1m 起伏路面时车体垂向加速度，如图12 所示。综上所述，优化结果较好地满足了悬架的设计要求，适用于双横臂式悬架系统的结构优化。

表4 定位参数变化范围Tab.4 The Variation Range of the Parameters

图12 过起伏路面时车体垂向加速度Fig.12 Vertical Acceleration of Vehicle Body over Polyline Road

5 结论

经过优化设计使得平台悬架稳定性能与减震缓冲性能有明显的提升，进而也提高了其自主控制过程中的路径跟踪精度与规划能力。应用Recurdyn 仿真软件可以使悬架系统的研发变的更加高效、便捷，大量缩短开发周期，减少研发成本，通过选择适当的优化方法可较好地实现悬架性能的优化。除此之外，提出的方法经过适当改进可用于其他类型的悬架系统优化设计。