二维Otsu拟合线阈值图像分割方法

梁义涛, 孟亚敏, 朱玲艳， 张 猛， 李永刚

(1.河南工业大学粮食信息处理与控制教育部重点实验室， 郑州 450001; 2.河南工业大学信息科学与工程学院， 郑州 450001)

图像分割是图像处理和分析中的关键一环，而阈值分割是图像分割中使用较多的基本和关键技术之一[1]。在阈值分割技术中，Otsu法[2]因其良好的实用化模型特点已被广泛应用在分类识别[3-6]、计算机视觉[7-10]等多个领域。1993年，针对经典Otsu法抗噪能力较差的问题，刘建庄等[11]提出了基于灰度图像的二维Otsu法。此方法考虑了像素本身及其邻域结构信息两方面影响因素，有很好的抗噪声性。但该方法假定了边界区域信息对于图像分割的影响可以忽略。此假设使得经典的二维Otsu法对于边缘信息较为丰富的图像分割效果不佳。因此，后续研究者给出了很多改进算法：范九伦等[12]提出了曲线阈值型Otsu法及其快速算法，经典的二维Otsu法可视为该方法的一种特例。但由于曲线阈值的解析式阶次需要提前人为设定，该文献快速算法依然是基于直线阈值近似地给出。如何针对不同图像自适应获得最优的曲线阈值解析表达依然是一个值得进一步探讨的问题。在直线阈值的求解方面，文献[13-15]结合对二维直方图的先验分析，给出了二维直方图区域斜分方法及改进，同时还将线阈值推广到法线与灰度级轴成任意θ角的直线。但该方法在实际应用时均固定选取θ=45°情况时直线阈值实现分割。且文献[14]指出需根据实际图像的信噪比及结果需求人为介入直线阈值θ角的值，使得该方法的自适应能力降低。受文献[16]的曲线阈值理论的启发，梁义涛等[17]提出了灰度图像二维Otsu折线阈值分割法。该方法本质上是曲线阈值思想在实际应用中的一种近似。仿真结果表明该方法对边界信息丰富的图像也能保持良好的分割效果。但是该方法需要事先针对不同的图像设定二维直方图迭代处理次数的经验值，降低了实际应用中自适应程度，且未对噪声污染图像的适用情况进行分析。

现在折线阈值法迭代思想的基础上进行改进，提出二维Otsu拟合线阈值分割法。改进和拓展主要涉及两方面：一是明确给出迭代停止的量化条件，提高算法的自适应能力；二是针对折线阈值法分类赋值过程烦琐、效率低的局限性，提出使用线阈值完成图像分割的思路。最后选取边界信息较为丰富的图像及含噪图像进行仿真实验，给出实验结果和分析，并从分割结果、抗噪性能和运行时间与相关算法进行比较与分析。

1 二维Otsu曲线阈值分割法

对于一幅M×N的数字图像，用f(x,y)表示图像上坐标为(x,y)的像素点的灰度，g(x,y)表示图像上坐标为(x,y)的像素点的3×3邻域平均灰度，g(x,y)的定义为

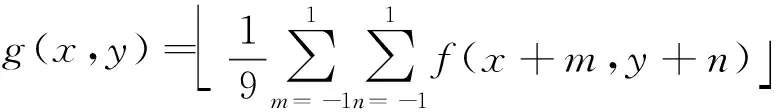
(1)

式(1)中：⎣」为取整；m为像素点左右位置；n为像素点上下位置。从g(x,y)的定义可以看出，如果图像的灰度级为L，那么相应的像素邻域平均灰度的灰度级也为L，f(x,y)和g(x,y)组成的二元组记为(i,j)。在此基础上定义图像的二维直方图，该二维直方图定义在一个L×L大小的正方形区域，其横坐标表示图像像元的灰度值,纵坐标表示像元的邻域平均灰度值。直方图任意一点的值定义为pij，它表示二元组(i,j)发生的频率。pij由式(2)确定，即

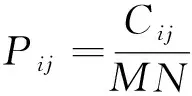
(2)

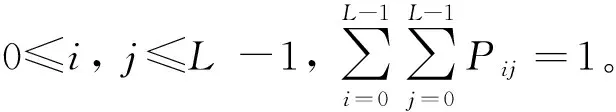
图1中，对角线上的两个区域Ⅰ和Ⅲ分别对应于背景和目标，远离对角线的区域Ⅱ和Ⅳ对应于边缘和噪声。在二维Otsu法中认为区域Ⅱ和Ⅳ的概率值近似为0，这种假设致使二维Otsu法忽略了边界区域的信息，造成了它在某些场合是不适用的。

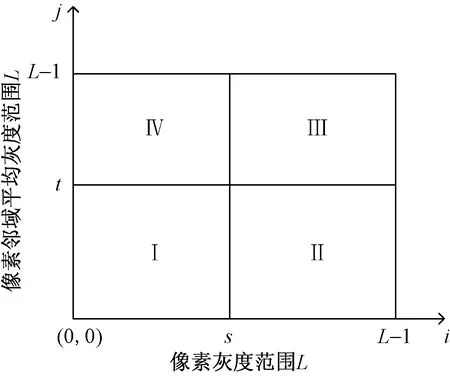
图1 二维直方图平面投影图Fig.1 Plane projection of two-dimensional histogram

文献[12]提出曲线阈值型Otsu方法。在该方法中，如果(s,t)是选取的阈值点，作过(s,t)的曲线r(i,j)将二维区域分成C0(s,t)和C1(s,t)两块，分别表示背景和目标，二维Otsu曲线阈值直方图如图2所示。

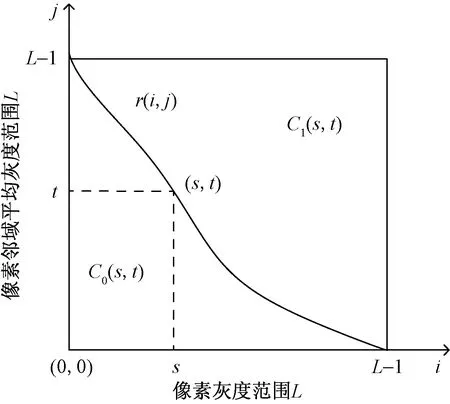
图2 二维Otsu曲线阈值直方图Fig.2 Threshold histogram of two-dimensional Otsu curve

背景和目标出现的概率分别为P0和P1,公式为

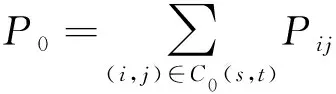
(3)

(4)

背景和目标对应的均值矢量为U0和U1，其表达式分别为

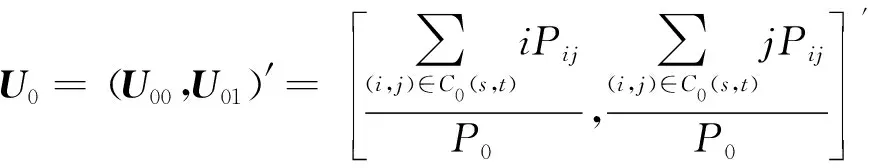
(5)

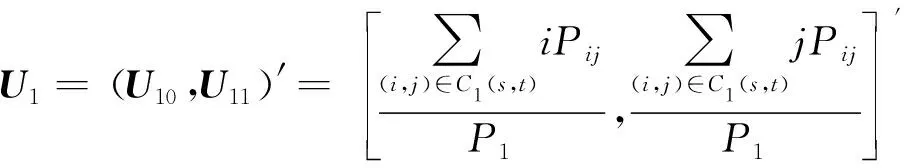
(6)

二维直方图上总的均值矢量为UT

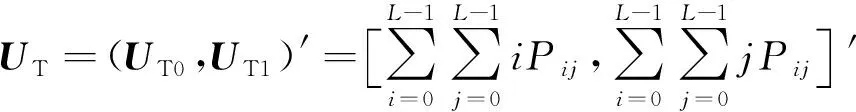
(7)

容易证明

P0+P1=1

(8)

UT=P0U0+P1U1

(9)

定义类间的离差矩阵SB为

SB=P0[(U0-UT)(U0-UT)′]+P1[(U1-UT)(U1-UT)′]=

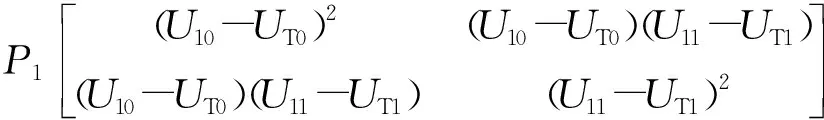
(10)

使用SB的迹作为类间的离散度测度,有

trSB=P0[(U00-UT0)2+(U01-UT1)2]+

P1[(U10-UT0)2+(U11-UT1)2]=

(11)

最佳阈值(s*,t*)由式(12)确定

(12)

由图2可以得出曲线r(i,j)取为(0,t)→(s,t)→(s,0)构成的折线，曲线Otsu选取r(i,j)为过(s,t)且垂直于二维直方图的定义域对角线的直线。通过i+j=s*+t*的直线，对原始图形进行分割，归类方式为

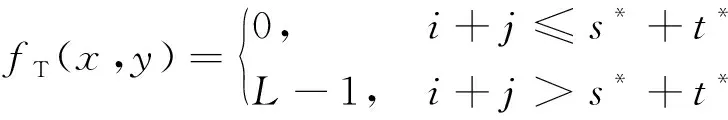
(13)

式(13)称为基于直线进行阈值选取的方法为二维直线阈值型Otsu法。

2 二维Otsu拟合线阈值分割法

2.1 算法思想介绍

在给出曲线Otsu法原理性描述之后，文献[12]指出，如何求解线阈值是一个关键问题。受此启发，基于逼近的思想和前期折线阈值法的研究，在二维Otsu折线阈值算法和曲线拟合方法的基础上，提出了另外一种易于工程实现的近似算法——二维Otsu拟合线阈值法。该方法用原二维Otsu法对边界信息或噪声所属区域的像素点迭代处理，获得多个阈值点；再将多个阈值点拟合成线阈值；以此线阈值作为分割标准实现分割。

假设由二维Otsu法获取最佳阈值点为(s*,t*)，t表示拟合的多项式，也用f(s)表示，a0表示常数项，n表示拟合曲线的阶次，an拟合多项式的系数，则过点(s*,t*)的最佳线阈值解析式可表示为

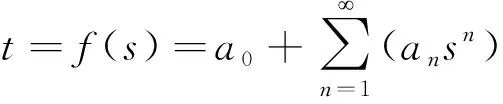
(14)

此时，问题转化为阈值曲线上点的分布区域和阶次的选取问题。由于阈值点(s*,t*)的存在，Ⅰ和Ⅲ区域的像素点是已经明确分类的像素点，而Ⅱ区域和Ⅳ区域包含的像素点为未分类的像素点。进而可知，阈值曲线上的各点必然分布在Ⅱ区域或Ⅳ区域，此时假定最终获取的最佳线阈值如图3所示。

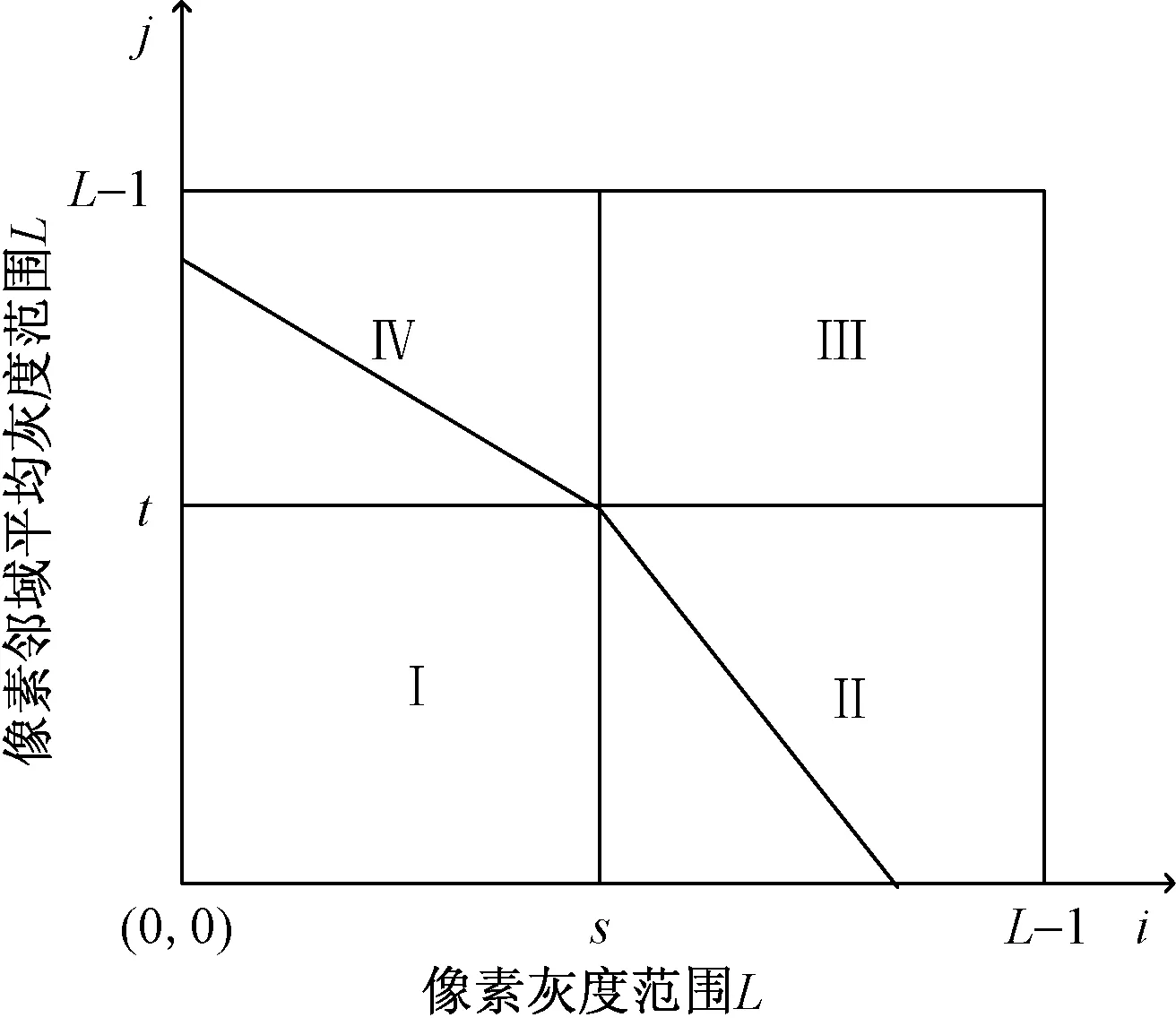
图3 最佳线阈值直方图Fig.3 Best line threshold histogram

任取曲线上一点，以该点为中心可将Ⅱ区域或Ⅳ区域细分为4个子区域。如此遍历曲线上点细分二维直方图，则可实现所有像素点分类。

2.2 算法流程介绍

输入：一幅彩色图像。

输出：分割好的黑白图像。

(1)灰度化并计算其邻域平均灰度值，组成图像二维直方图。

(2)利用原始二维Otsu法，得到阈值点。

(3)判断Ⅱ、Ⅳ区域像素占整幅图像像素的比率是否小于0.02，如果比率和小于0.02，停止处理；如果比率和大于或等于0.02，则Ⅱ、Ⅳ区域成为新的待处理区域，条件不满足则不断迭代处理。

(4)判断阈值个数是否大于1，如果阈值个数大于1，用最小二乘法将这些点拟合成阶次为n的曲线，称为线阈值,以此线阈值作为分割标准，如果阈值个数等于1，以此阈值作为分割标准。

(5)根据分割标准，得到二值化图像，实现分割。算法流程如图4所示。

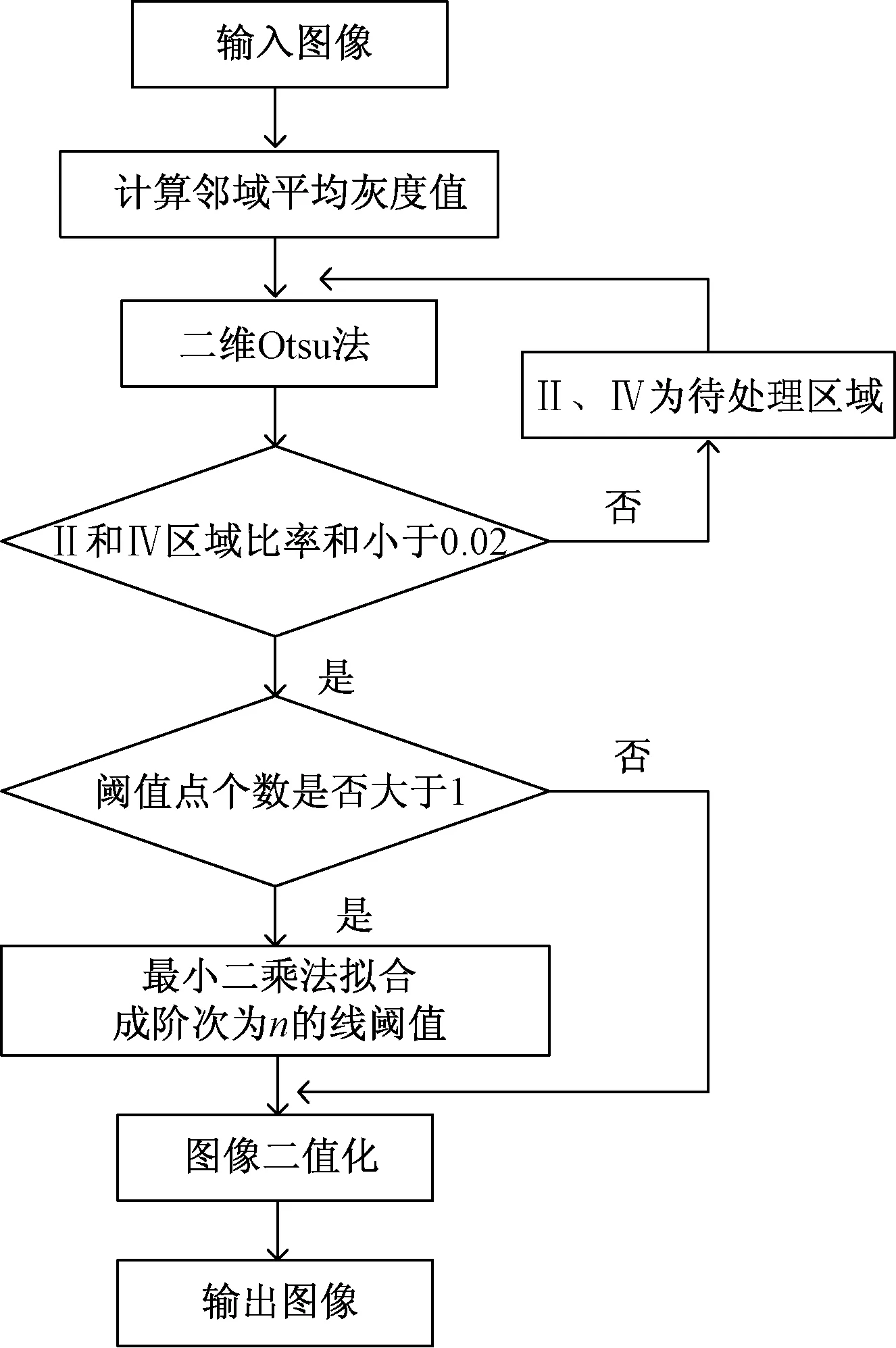
图4 算法流程图Fig.4 Algorithm flow chart

2.3 迭代处理

本文方法在文献[17]折线阈值法的迭代思想基础上提出迭代停止条件为该类像素点概率满足小概率事件的概率标准要求(称为小概率设定值ε)时停止迭代。

具体的过程说明如下：用二维Otsu法处理，获取初次阈值点(s*,t*)，依照点(s*,t*)将坐标系对应区域分为四个子区域：Ⅰ和Ⅲ区域为目标和背景区域，Ⅱ和Ⅳ区域为边缘信息或噪声。统计属于Ⅱ区域和Ⅳ区域灰度像素的概率和，判断Ⅱ和Ⅳ区域的概率和是否小于ε。如果概率和大于或等于ε，则利用二维Otsu法再分别处理区域Ⅱ和Ⅳ区域，再次获取对应阈值点，如图5所示。如果概率和小于ε，则停止迭代。

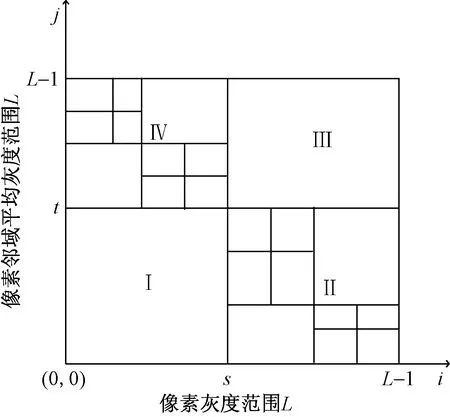
图5 迭代处理图Fig. 5 Iterative processing diagram

利用二维Otsu进行迭代对Ⅱ、Ⅳ区域的像素逐级分类处理，最终达到使得Ⅱ、Ⅳ区域像素数达到可忽略的标准(概率上可以认为Ⅱ、Ⅳ区域未分类像素数占整幅图像总像素的比率满足小概率事件标准)。

从不同设定值ε的运行时间进行分析比较研究。为方便比较起见，其中，拟合曲线选择过点(s*,t*)的两段直线[以点(s*,t*)为界，分别在Ⅱ区域和Ⅳ区域各拟合一条直线],噪声密度标准差设定为20。

通过对6幅图像(图6)进行实验，统计了6幅图像的Ⅱ、Ⅳ区域像素占整幅图像像素的百分比，如表1所示，分别用n(Ⅱ)/N和n(Ⅳ)/N表示；Ⅱ区域和Ⅳ区域的像素占整幅图像像素的百分比，用n(Ⅱ、Ⅳ)/N表示。其中，n表示该区域的像素数，N表示整幅图像的像素数。

图6 输入图像Fig.6 Input image

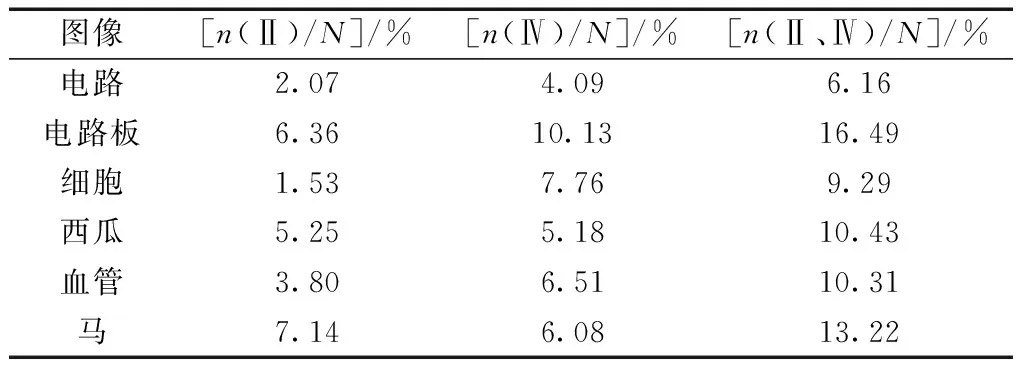
表1 图像直方图未分类区域像素比例

从表1统计的数据可看出，Ⅱ、Ⅳ区域的像素比例远大于可以忽略的条件，所以对其进行处理是必要的。而且如果对边界处理要求较高，Ⅱ、Ⅳ区域的处理结果也很重要。

在概率论中一般将概率在0.01～0.05的事件称为小概率事件，所以表2中ε选取0.01、0.02、0.05做实验，统计了3幅图像的阈值点和运行时间，其中运行时间是取3次实验的平均值。

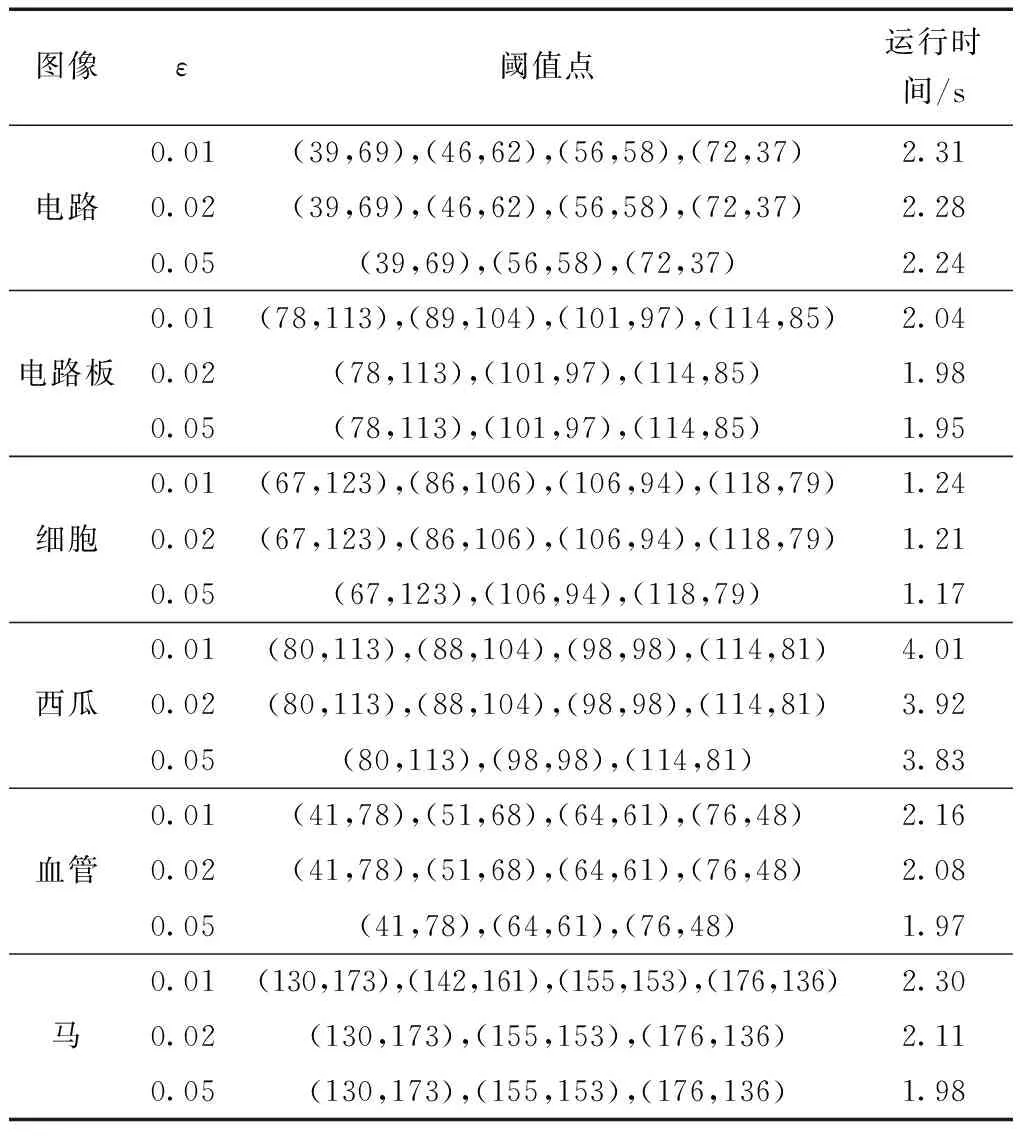
表2 不同小概率设定值ε的影响比较

从表2中阈值点个数的数据可看出，ε为0.01时需要处理像素最多，ε为0.05时需要处理像素最少，随着ε变大，运行的时间变短。比如对于图6的电路，ε选取0.01和0.02得到的阈值点个数相同，但对于ε选0.02来说，ε选0.01会处理像素更多，所以ε选0.01运行时间长，ε选取0.05时迭代次数减少，运行时间短。计算图6的电路的运行时间，ε取0.05比ε取0.01运行速度提高了3%。

由图7的实验结果可得，针对不同要求的实际应用，可以选择不同的ε值。选择设定II、IV区域未分类像素占整幅图像的百分比小于0.02达到可忽略不计的标准，以ε=0.02为例做实验。

图7 不同小概率设定值的实验结果Fig.7 Experimental results of different small probability settings

2.4 拟合线阈值

实际中，拟合曲线的阶次n不可能无限大，且拟合多项式阶数n>5时，其法方程的系数矩阵是病态的。因此，考虑过拟合、实现效率等问题，这里假定n>3时，曲线阈值错分类像素点数可忽略。下面为分别以阶数n=1、2、3进行分割的比较研究实验。仿真结果如图8所示。其中，小概率设定值为0.02，噪声密度标准差设定为20。

图8 不同阶数的实验结果Fig.8 Experimental results of different orders

通过迭代处理得到的多个阈值点，用最小二乘法拟合这些阈值点得到线阈值，作为分割标准，从图8可以看出，拟合曲线阶数n=1处理效果很好，因此设定拟合曲线的阶次为1。

3 实验结果及分析

实验硬件配置为Intel(R) Core(TM) i5-3210MCPU @2.50 GHz 4GB RAM的PC机，软件使用MATLAB R2017b进行实验。实验的算法包括原始二维Otsu法，改进的灰度图像二维Otsu折线阈值分割法，改进的二维直方图区域斜分算法及本文方法。通过实验，验证了本文方法的可行性，通过方法的对比，说明此方法提高了分割质量和普适性。

3.1 分割性能实验

为验证本文方法的可行性，以下给出图像的实验结果，实验图像依次为：电路、电路板、细胞、西瓜、血管和马。实验方法依次为原始二维Otsu法、二维Otsu折线法、二维Otsu斜分法、本文方法。

3.2 抗噪声性能实验

为验证本文方法的抗噪性，用lean图像做实验，在原图加入不同程度的高斯噪声，图10为加入不同高斯噪声不同算法实验结果。图10(a)～图10(d)、图10(e)～图10(h)、图10(i)～图10(l)分别加入标准差为10、20、30的高斯噪声，使用的分割方法分别为原始二维Otsu法、二维Otsu折线法、二维Otsu斜分法、本文方法。

3.3 实验分析

图9(e)～图9(h)和图9(u)～图9(%)是存在较多噪声点的一个典型情况，二维Otsu折线法和二维Otsu斜分法的处理效果比原始二维Otsu法的要好很多但是这两种方法的自适应能力较差，本文方法能自适应处理并且处理效果较好。

由图9(i)～图9(l)可以看出，原始二维Otsu法和二维Otsu折线法处理的结果没有分割出右下的细胞，二维Otsu斜分法和本文方法可以将弱对比度的细胞也分割出来，图9(a)～图9(d)的右上区域，因为光照原因二维Otsu法、二维Otsu折线法和二维Otsu斜分法处理结果不好，区域的线路没有分割出来，本文方法将这部分区域的线路清晰分离出来。由图9(a)～图9(d)、图9(i)～图9(l)可知，对于对比度较弱或者有弱光影响下，本文方法处理效果好且自适应性强。由图9(q)～图9(t)和图9(m)～图9(p)可以直观地看出，本文方法对边缘处理效果更好。

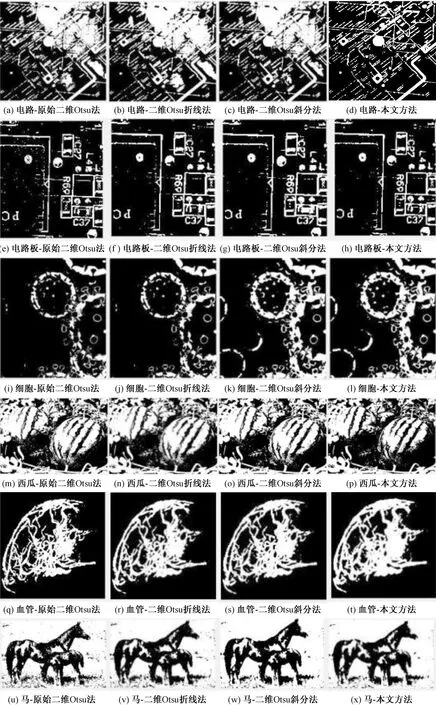
图9 不同算法的实验结果Fig.9 Experimental results of different algorithms

图10为本文方法的抗噪声实验结果，可以看出本文方法比其他方法的抗噪性更好，并且噪声越大越能突出本文方法的抗噪性越强。

图10 加入不同高斯噪声不同算法实验结果Fig.10 Experimental results of different algorithms with different Gaussian noise

与二维Otsu折线阈值法比较，二维Otsu折线阈值法需要自己确定迭代次数，降低了智能自动程度，本文方法的改进主要是确定了迭代分割的次数，保持了原始二维Otsu法的自动性，处理时间也比二维Otsu折线阈值法快。

表3是本文方法得到的阈值点及线阈值，ε设定为0.02，n设定为1，噪声标准是20，x表示像素的灰度，y表示像素的邻域平均灰度。

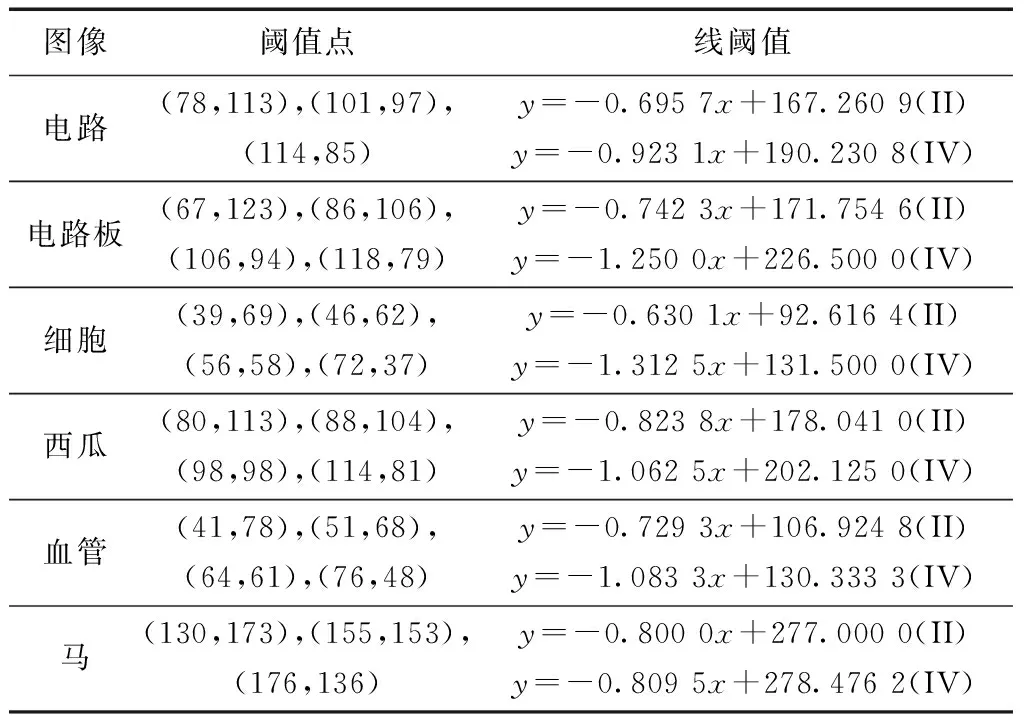
表3 实验图像的分割线阈值

3.4 分割质量评价

主观评价图像分割质量的方法主观性强，因此对图像分割质量的客观评价是必要的。

采用最大相关准则(MCC)作为评价函数[17]。最大相关准则是Yen等[18]基于最大熵准则提的，相关数总量与分割质量成正相关的关系。陈修桥等[19]将一维最大相关准则推广至二维。表4为四种算法分割结果的定量评价，本文算法在主客观上一致，有较好的视觉效果和相关数指标。

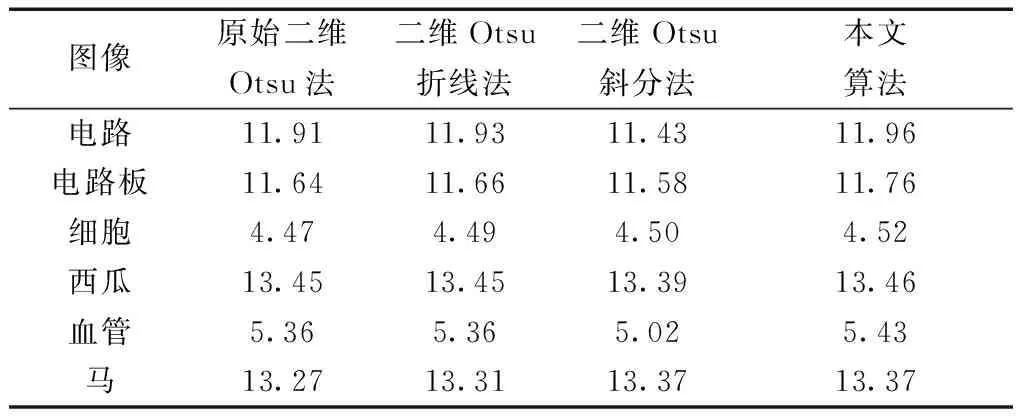
表4 不同算法分割结果的定量评价

峰值信噪比(PSNR)[20]是衡量算法抗噪性能的量化指标，PSNR越大，表示算法的抗噪性能越好。从表5可知，本文算法和二维Otsu折线法随着噪声程度变大，PSNR变大；另外两种算法随着噪声程度变大，PSNR变小。证明了本文算法的抗噪声能力，并噪声程度越大，本文算法效果越好。

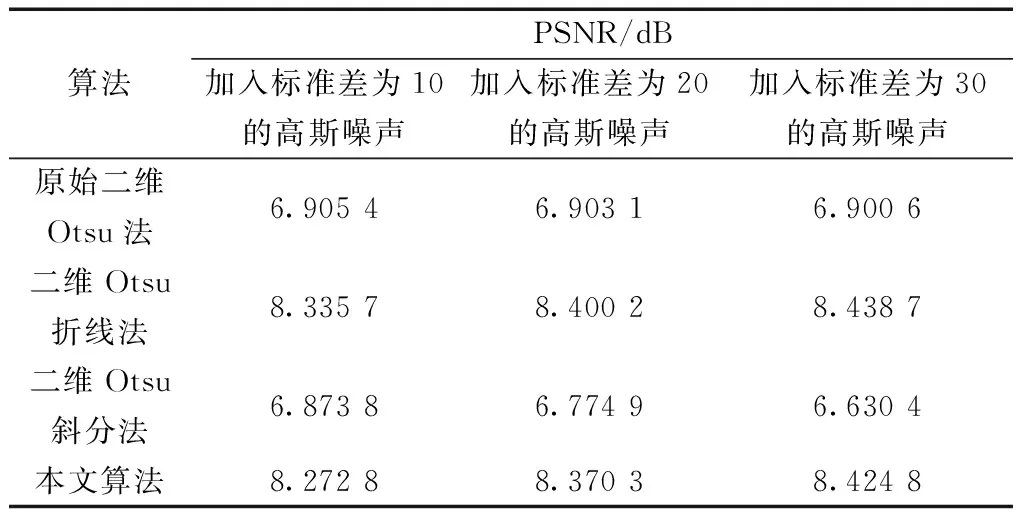
表5 不同算法对噪声图像分割的PSNR数据对比

4 结论

(1)对于二维Otsu法及改进的方法存在的问题：不合理忽略像素和普适性低，提出二维Otsu拟合线阈值图像分割法，通过原始二维Otsu法对二维直方图分区，若边缘信息或噪声区域占整幅图像像素的比率达到在概率上可以忽略的小概率事件，则合适忽略，否则用原始二维Otsu法继续迭代处理边缘信息或噪声区域，解决了经典二维Otsu法在实际应用中可能存在的假设前提不合理的问题；若边缘信息或噪声区域占整幅图像像素的比率本就小于小概率事件概率，则直接用阈值进行分割，解决了普适性低的问题。

(2)拟合阈值是对文献[12]提出的曲线阈值的一种应用近似，且解决了最优阈值为曲线时得到解析式困难的问题。如果最终采用了一次解析式拟合阈值时，针对不同的图像，其自动生成的线阈值斜率是不同的。这就解决了文献[14]中线阈值的斜率需要人为设定的问题。

(3)在迭代处理环节，本文算法基于折线阈值法的思路进行改进，加入量化的迭代停止条件，提高了算法的自适应能力。在分类赋值方式上，引入曲线拟合方法，相对折线阈值法而言，简化实现过程，提高了算法执行效率。

(4)实验结果表明，本文方法对边缘信息丰富并且要求分割质量高的图像处理效果更好。本文方法保持了原始Otsu法的自适应性，提升了算法的普适性。