基于潮汐调和分析的全球定位系统-多路径反射测量技术潮位预报
王 森, 刘立龙, 黄良珂, 周 威
(1.桂林理工大学测绘地理信息学院, 桂林 541004; 2.广西空间信息与测绘重点实验室, 桂林 541004; 3.海军工程大学电气工程学院, 武汉 430079)
潮位的准确监测和预报对于水利工程建设、港口航道设计、潮汐发电和风暴潮预警等具有重要的意义[1]。目前,沿岸潮位的监测、预报多采用验潮站进行监测,存在着验潮站随着固体潮和海洋负荷变化而运动的问题,故难以准确监测潮位的绝对变化[2]。基于全球定位系统的多路径反射(global positioning system-multipath reflection,GPS-MR)测量技术可以有效监测潮位变化,且能克服传统验潮站海陆基准难以统一的问题[3]。因此,GPS-MR可以作为潮汐变化监测的重要补充手段。
GPS-MR技术是全球定位系统反射(global positioning system-reflection,GPS-R)测量的一类[4]。不同于传统的双天线GPS-R,GPS-MR技术不需要特制的接收机和天线,仅采用大地型测量接收机和右旋极化天线,通过分析GPS直反射信号的干涉效应在信噪比(signal-to-noise ratio, SNR)上的变化来反演地表环境参数[5]。该技术相对于传统的双天线GNSS-R来说,节约监测成本,便于推广应用。中外对GPS-MR监测的研究已经取得了一定成果,并将其应用于海平面高度测量[6]、雪深测量[7]、土壤湿度[8]以及植被监测[9]。诸多学者针对GPS-MR潮位反演做了大量有意义的工作,文献[10]采用卡尔曼滤波方法对SNR原始序列进行滤波,削弱了GPS信噪比数据中的粗差对反演的影响;文献[11]考虑了潮位的瞬时变化,构建了顾及海平面变化速率的GPS-MR潮位反演模型;文献[12]采用经验模态分解方法提取SNR反射信号,剔除了部分非海面反射低频信号的影响;文献[13]联合了GLONASS(俄语“全球卫星导航系统”)、BDS系统(北斗卫星导航系统)进行反演,将单系统GPS-MR扩展到多频多模GNSS-MR,提高了潮位反演的时间分辨率。
虽然诸多学者针对GPS-MR开展了广泛的研究,但主要是针对GPS-MR反演模型进行改进,以提高其反演精度及时间分辨率为目的,较少学者关注长周期的GPS-MR潮位反演结果用于潮汐分析和预报应用。而潮位的预报也是验潮站所承担的另一个主要功能,因此现利用一年的GPS-MR潮位反演结果,构建1 h GPS-MR潮位反演序列用于潮汐调和分析和预报,验证GPS-MR反演潮位替代验潮站进行潮位预报的可行性。
1 GPS-MR潮汐预报模型
1.1 GPS-MR潮位监测原理
多路径效应是GPS测量中最重要的误差源之一。由于地表的反射,GPS接收机会同时接收来自GPS卫星的直射信号和地表的反射信号,直反射信号在接收机内部产生干涉,并反映在接收信号功率的变化上[13]。信号的质量通常用SNR来衡量,定义为噪声功率PR与信号功率N的比值,即
SNR=PR/N
(1)
RINEX标准文件里记录的实际载噪比(C/N0)为观测值,其与SNR的关系为C/N0=SNRBn,其中Bn为噪声带宽,为了方便计算,一般假设Bn=1 Hz,即可将载噪比观测值转化为信噪比观测值。
如图1所示为信噪比原始序列,可以看出大地型GPS接收机的SNR观测值呈抛物线趋势,且伴随着不等振幅的震荡。由于直射信号功率远大于反射信号功率,可以认为该SNR震荡由反射信号所引起。采用二次多项式去除该信噪比的趋势项,得到该信噪比的残差序列(SNR震荡),记为dSNR,该残差序列呈现出余弦函数的形式[14]可以表示为
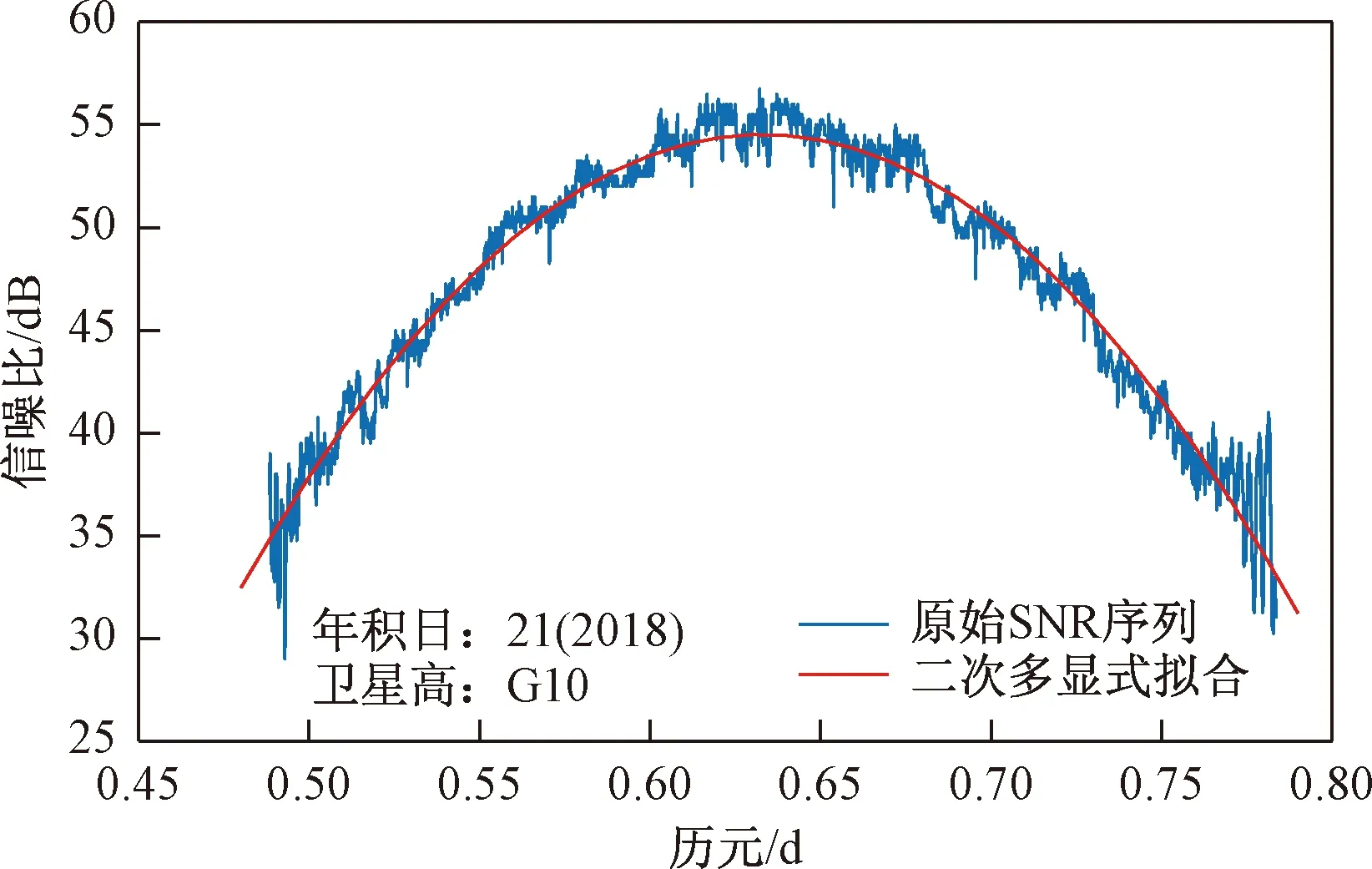
图1 信噪比原始序列Fig.1 Original sequence of SNR
dSNR=Acos(4πhsinθ/λ+φ)
(2)
式(2)中:A为振幅;λ为波长;h为接收机天线中心到反射面的垂直距离;θ为卫星高度角;φ为信噪比残差相位。根据式(1),可以从信噪比残差序列求出垂直反射距离h,并通过式(3)求得潮位高:
hGPS-MR=HGPS-Htide-h
(3)
式(3)中:HGPS为GPS天线处的绝对高程;Htide为验潮站数据起算面的绝对高程。
显然,如式(3)所示,垂直反射距离h的获取是GPS-MR潮位反演的关键。令f=2h/λ,可转化为对信噪比残差序列频率f的计算。现采用Lomb-Scargle(LS)频谱分析方法获取其频率f,进而求得h,达到GPS-MR潮位监测的目的。
1.2 潮汐分析预报原理
海水受到月球和太阳引潮力的作用产生规律性的上升下降运动称之为海洋潮汐。海洋学家提出了平衡潮理论用于解释潮汐现象,但却难以将该理论用于潮汐预报[14]。为解决该问题,将平衡潮分解为一系列分潮,引入潮汐调和常数,得到分潮的表达式,然后将各个分潮叠加起来,可得到实际的潮高公式[式(4)],利用此式即可完成潮汐预报。

(4)
式(4)中:A0为分析期间的平均海平面高;σi为分潮的角速度;fi为交点因子;Hi为分潮的平均振幅,G(V0+u)为分潮的格林威治时初相角;gi为区时迟角。其中,Hi和gi随分潮和地点而变化,但对具体分潮具体地点是常数,称之为潮汐调和常数。
不考虑非天文潮位,又视平均海面A0为σ=0°/h的一个特殊分潮。


(5)
通过潮汐调和分析求出A、B的值,即可求得分潮的调和常数。
1.3 基于GPS-MR的潮位监测和预报
利用式(4)进行潮汐预报时,需要等时间间隔的潮位观测序列。采用三次样条函数对式(3)中GPS-MR反演潮位值进行拟合,并采样成1 h时间分辨率的潮位序列数据,利用该序列数据进行潮汐分析和预测。其主要流程如图2所示。

图2 GPS-MR潮位预测流程Fig.2 Tide prediction based on GPS-MR
2 实验分析
2.1 数据来源
SC02 GPS观测站位于美国西海岸Friday港,由美国大陆板块边缘观测组织(PBO)负责建设维护。PBO官网(https://www.unavco.org)可以提供不同采样间隔的观测数据和导航数据。SC02观测站建设在基岩上,三面临海,天线离海平面高度在5~8 m,可以作为GPS-MR潮位监测站。
Friday验潮站距离SC02观测站300 m处,可以认为验潮站具有与SC02观测站具有相同的水文数据。该验潮站位于美国西海岸维多利亚港,由美国海洋和大气管理局(NOAA)进行维护,使用NG3000水位传感器,精度可达毫米级,可以作为GPS-MR潮位反演及预测的有效验证,数据下载地址为https://tidesandcurrents.noaa.gov/。SC02 GPS测站与验潮站的位置如图3所示。

图3 SC02和验潮站位置图Fig.3 SC02 and tide station location map
2.2 GPS-MR潮位反演实验
选择GPS系统S1信噪比数据进行GPS-MR潮位反演。反演策略为:高度角区间为5°~12°,避免SNR弧段过长海面环境变化导致反演结果异常,又克服了弧段过短LS频谱分析难以得出正确频率的问题[15];方位角区间为50°~240°,选择依据为第一菲涅尔反射区和测站环境[16],如图4所示。

图4 SC02测站有效探测范围Fig.4 Effective detection range of SC02 GNSS station
如图5所示为1 d的GPS-MR潮位反演结果。由图5可见,GPS-MR反演潮位能较好地捕捉到潮位的变化趋势,但仍有部分结果存在偏差。对GPS-MR反演潮位的精度进行统计,其与验潮站潮位参考值的均方根误差(root-mean-square error,RMSE)为0.14 m,平均绝对误差(mean absolute error, MAE)为0.10 m,低于湖面GPS-MR水位反演的精度,原因在于海面易受到风速、海平面变化以及海浪的影响,这也是制约GPS-MR潮位反演精度的主要因素。

图5 GPS-MR反演潮位结果Fig.5 Result of the tide based on GPS-MR
为了进一步说明GPS-MR潮位监测可行性,以 1 a 的数据进行分析。由于2017年2月验潮站数据缺失严重,故选取2017年3月1日—2018年3月1日的数据进行实验,结果如图6所示。显然,GPS-MR反演潮位与验潮站潮位符合性较好,但时间分辨率却不及验潮站实测数据。原因是本文仅采用了经典LS频谱分析方法,加窗LS频谱分析方法虽然可以得到更多的反演个数,但却牺牲了反演精度,故本文不采用该方法[15]。

图6 GPS-MR反演潮位Fig.6 Result of the tide based on GPS-MR
如图7所示为GPS-MR反演潮位与验潮站潮位之间的相关系数图。统计GPS-MR潮位反演的精度,其与验潮站参考潮位的RMSE为0.16 m,MAE为0.11 m,相关系数为0.969 7。显然,采用GPS-MR进行潮位监测是可行的。

图7 GPS-MR反演潮位与验潮站潮位相关性Fig.7 Correlation between GPS-MR inversion and tide station
2.3 GPS-MR潮汐预报
GPS-MR潮位监测受海风、海平面变化等影响,会导致反演结果出现偏差。为了减少粗差对GPS-MR潮汐预测的影响,采用样条函数对GPS-MR潮位结果进行拟合,重采样出1 h时间分辨率的GPS-MR潮位序列,部分结果如图8所示。
由图8可见,显然有部分GPS-MR潮位反演结果出现了较大偏差,而采用样条函数拟合的GPS-MR潮位能“光滑”掉部分离群值,同验潮站的符合性更好。

图8 GPS-MR反演潮位三次样条函数拟合Fig.8 GPS-MR inversion after cubic spline function fitting
GPS-MR反演潮位经样条函数拟合后精度统计结果如表1所示。结果表明,经过样条函数拟合后的MAE和RMSE分别提高了44.1%(0.056 m)和32.2%(0.051 m),相关系数提高到0.991。

表1 GPS-MR样条函数拟合潮位精度
使用T-tide潮汐调和分析工具箱对1 h分辨率的GPS-MR潮位反演序列进行调和分析,共得到67个分潮[17]。潮汐调和分析时,一般考虑11个主要分潮的影响,采用其中的8~11个显著分潮即可取得较好的预报效果[18]。分潮SNR是衡量分潮是否显著的主要依据,通常认为SNR>2的分潮为显著分潮,计算方式为分潮振幅与振幅误差比值的平方[14]。这里计算了10个显著分潮的调和常数,并与验潮站潮位的调和常数作为对比,结果如表2所示。
如表2所示,GPS-MR潮位序列的潮波系数和验潮站实测潮波系数相差不大。其中,除P1和K2分潮外,所有分潮的振幅偏差都在1 cm左右,相位迟角偏差都小于10°,可以满足潮汐预测的要求。
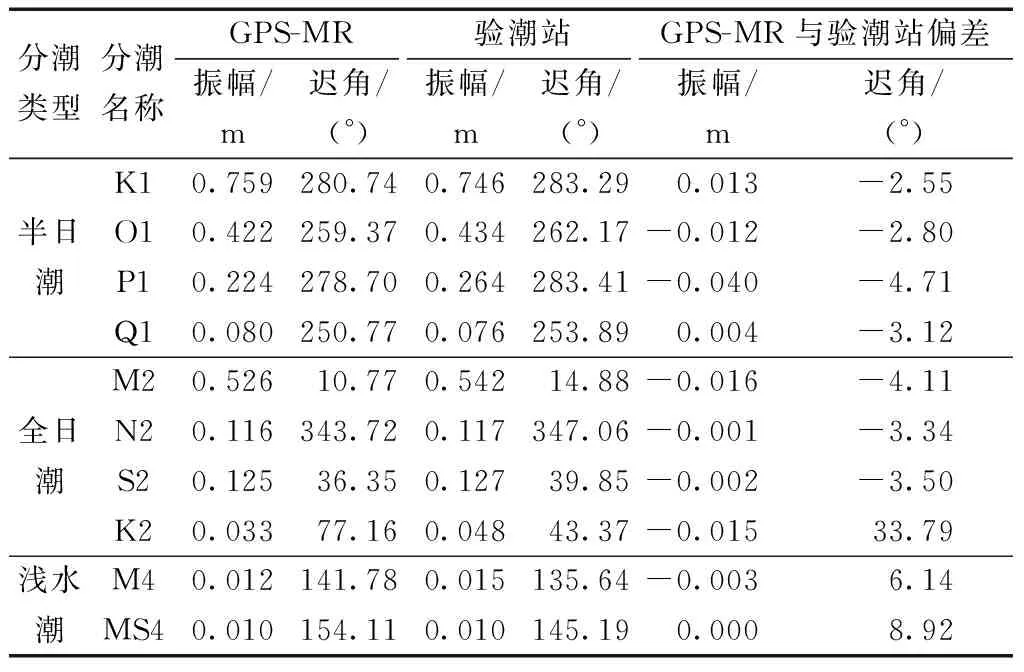
表2 GPS-MR潮位序列和验潮站潮位调和常数
分别利用GPS-MR潮位调和常数和验潮站潮位调和常数预报2018年3月3日—4月1日的潮位,并与验潮站实测潮位进行对比,结果如图9所示。

图9 GPS-MR潮位序列预测结果(2018年)Fig.9 The results of tide level series prediction based on GPS-MR(2018)
由图9可知,GPS-MR以及验潮站潮位预报值与验潮站潮位实测值总体较为一致,能较好地捕获潮汐的峰值和谷值。GPS-MR潮位预报和验潮站潮位预报出现了一致的余差,原因是采用潮波调和分析方法预报潮位主要考虑了天文潮因素的影响,针对大洋潮汐精度较高,而SC02测站和验潮站都位于海湾内部,四周分布着密集的海岛,且有河流汇入,外界环境的变化导致分潮之间产生了非线性的干涉,这就导致了潮汐预测的困难。
为进一步说明GPS-MR潮位序列的预测效果,统计了GPS-MR潮位预测的结果如表3所示。由表3可见,GPS-MR预测与验潮站实测潮位的相关系数为0.97,平均绝对误差(MAE)为0.11 m,均方根误差(RMSE)为0.14 m,与采用验潮站数据预测精度相当。受限于潮汐调和分析潮位预报法的精度限制,虽然对某些非线性潮波没能达到很好的精度,但采用GPS-MR反演潮位进行潮位预报仍是可行的。
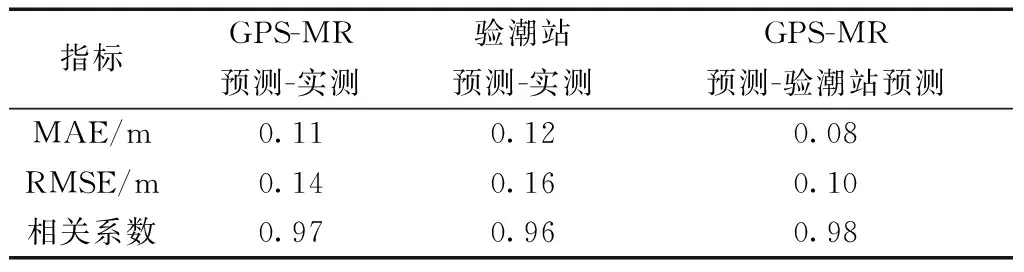
表3 GPS-MR潮位预测值与验潮站实测值的相关性
3 结论
针对传统验潮站功能单一的问题,采用GPS-MR方法进行潮位反演,并利用等间隔的GPS-MR反演潮位序列进行潮汐预报。结果表明:
(1)GPS-MR潮位反演可以较好地监测潮汐的周期变化,精度可以达到分米级。
(2)利用GPS-MR反演潮位结果进行潮汐调和分析预报与利用验潮站潮位预报结果相差不大,与验潮站实测潮位的均方根误差在0.14 m左右,采用GPS-MR进行潮汐预报是可行的。
由于海风、陆地以及气象因素等的影响,真实的潮汐往往是非线性、复杂的,后续将对高精度GPS-MR潮位预报方法展开进一步研究。

