装载机工作装置载荷数据模型与载荷谱编制∗

万一品，宋绪丁，员征文，田维波

（1.长安大学道路施工技术与装备教育部重点实验室 西安，710061）

（2.徐工集团江苏徐州工程机械研究院 徐州，221004）

引言

装载机工作装置抗疲劳设计和疲劳试验时须确定与实际作业工况相符的载荷谱，常利用程序载荷谱在试验台上再现机械结构所承受的随机载荷［1-2］。

Yan等［3］借助当量寿命概率分布，在保持载荷时间历程与状态参数一致的前提下编制了飞机结构的疲劳载荷谱。文献［4-5］运用轮心位移反求汽车车身的当量外载荷，结合多体动力学编制了汽车车身载荷谱。于佳伟等［6］在汽车室内模拟实验中，将汽车实测载荷时间历程编制成试验用载荷谱，应用于耐久性试验中。文献［7-8］研究了铁路货车车钩与车体的载荷谱编制与疲劳寿命预测方法，编制的加速试验谱减少了车钩疲劳试验次数。高云凯等［9］则利用外载荷编制的程序载荷谱实现了汽车车身的疲劳台架试验和寿命预测。装载机载荷谱的研究多集中在传动系，张英爽等［10］测试了装载机传动系载荷，编制了疲劳试验载荷谱。装载机结构件的研究多集中在静强度分析、动力学仿真以及基于仿真的结构优化分析［11］，对载荷谱的相关研究很少。

文献［12］给出了装载机斗尖载荷水平、竖直等不同分量的载荷谱，然而在疲劳台架试验加载时很难保持不同分量载荷谱之间的相位关系。笔者确定了装载机工作装置固定姿态下的外载荷与动臂铰点载荷当量关系，建立了核密度估计和参数分布估计两种外载荷数据模型，编制载荷谱并通过损伤试验分析了两种载荷数据模型编谱结果的差异。

1 装载机工作装置外载荷当量

装载机工作装置由铲斗、连杆、动臂、摇臂、动臂油缸和摇臂油缸铰接组成，在油缸作用下实现物料铲装和卸载。工作装置在一个作业循环内测得的载荷对应不同作业姿态，获得固定姿态下的当量载荷是编制疲劳试验载荷谱的基础。实测大载荷出现在铲掘时刻，选择铲掘作业姿态为外载荷当量姿态，保证对结构损伤影响大的载荷与实际一致［13］。将装载机所受外载荷简化为作用在铲斗的集中载荷，固定姿态下的装载机当量外力如图1所示。图中：A，B，C，D，E，H，J，K，L分别为各结构铰接点；O点为当量外力作用点；FO装载机当量外力；θ1为力FO与水平方向的夹角；l和h分别为O点到点A水平和竖直方向的距离；FE和FL分别为摇臂油缸和动臂油缸支反力。

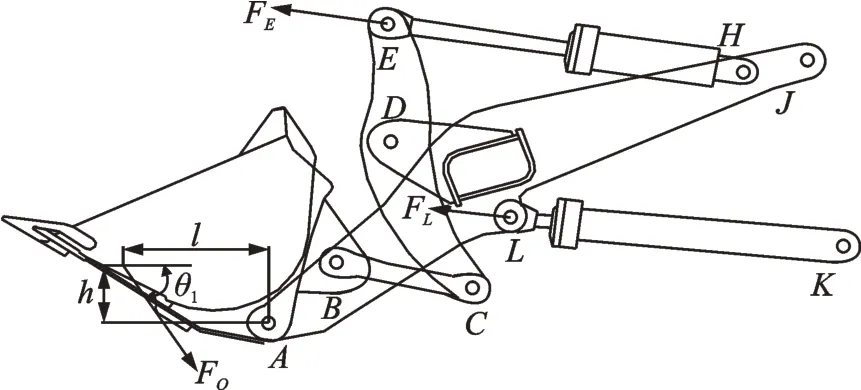
图1 固定姿态装载机外力当量Fig.1 External force equivalent indication of fixed attitude

装载机在铲装物料时，动臂油缸为支点，视动臂结构为悬臂梁，选取动臂板上弯矩作为外力当量的中间变量，保证动臂结构在实际作业过程中，不同作业姿态下的截面弯矩与疲劳台架试验时保持一致，从而确保疲劳台架上动臂的整体受力状态与实际铲装作业状态一致。

装载机当量外力FO及其作用于铲斗的位置参数l，h和θ1是未知量，以动臂铰点AJ连线为x'方向建立动臂局部坐标系x'Jy'，已知动臂局部坐标系下各铰点受力，便可求得动臂截面弯矩。动臂局部坐标系下动臂截面弯矩如图2所示。

图 中：FAx'，FAy'，FDx'，FDy'，FLx'和FLy'分 别 为动 臂铰点A，D，L上受力在动臂局部坐标系x'和y'方向的分力；O1，O2，O3和O4为动臂不同截面处的弯矩计算点；O5为动臂最大弯矩截面弯矩点。

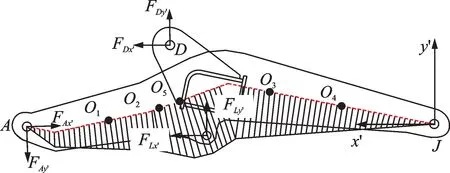
图2 装载机动臂截面弯矩示意图Fig.2 Sketch diagram of cross-section bending moment of loader boom

利用文献［14］中载荷测试系统，实测LW900K装载机在大石方、黏土、铁矿粉和小石方物料下铲斗铰点力和动臂、摇臂油缸位移数据，求得固定姿态时当量外力FO作用位置和方向参数h为176 mm，l为818 mm，θ1为65°。由文献［15］中弯矩当量计算公式得到4种物料下当量外力时间历程如图3所示。

2 参数分布估计载荷模型与载荷谱

参数分布估计外载荷数据模型是利用联合概率密度函数的相关分布参数，计算对应载荷均幅值不同分级下的频次数，编制载荷谱。由正态分布和三参数威布尔分布得到确定载荷谱各级频次的均幅值联合概率密度函数［10］如式（1）所示

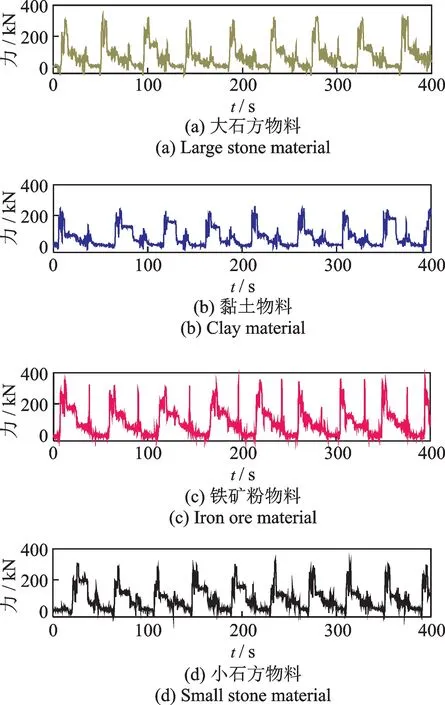
图3 不同物料下外载荷当量结果Fig.3 External load equivalent results for different materials

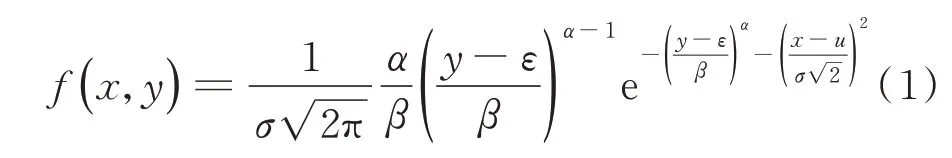
其中：x和y分别为载荷均值和幅值；u和σ分别为正态分布的均值和标准差；α，β和ε分别为威布尔分布的形状、尺度和位置参数。

第a级均值和第b级幅值的载荷循环数Nkab由均幅值联合概率密度函数的积分求得，外载荷数据的数学模型为

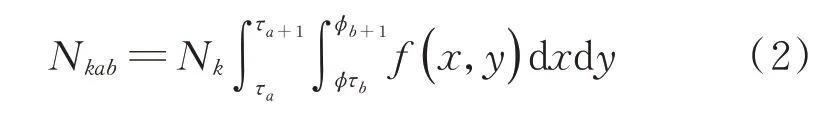
其中：Nk为工况k的扩展频次，k取1，2，3，4；τa和τa+1分别为第a级均值的下限和上限；φb和φb+1分别为第b级幅值的下限和上限。

将一个载荷循环总频次为106次的完整谱块的载荷总频次按照式（3）分配给4种作业物料工况

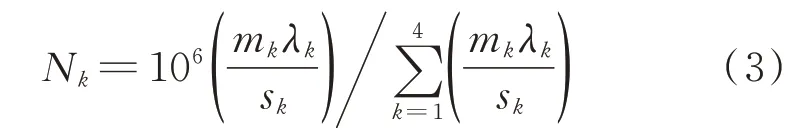
其 中：mk，λk和sk分 别 为 工 况k对 应 物料 雨 流 计 数 所得循环数、所占时间比例与实测作业斗数。

多物料工况合成后的二维载荷谱第a级均值和第b级幅值的循环数Nab由式（4）求得

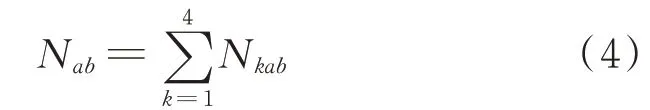
用正态分布和三参数威布尔分布得到4种物料参数分布估计外载荷数据模型中均幅值联合概率密度函数的未知参数拟合结果如表1所示。

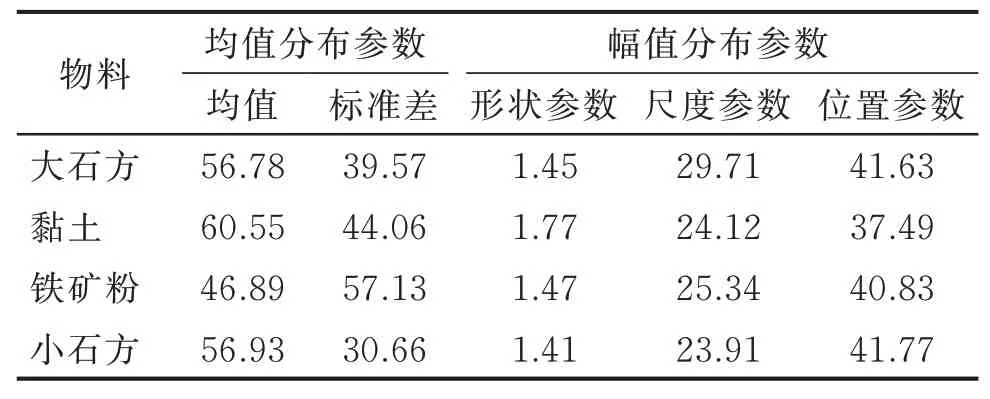
表1 参数分布估计载荷数据模型参数Tab.1 Parameters of parameter estimation model

试验样机4种物料调研所得的各工况时间比例和按照式（3）所得载荷扩展频次如表2所示。

表2 载荷扩展频次数据Tab.2 Expansion frequency data of load

联立式（1）～式（4）并代入表1和表2中数据，均值采用等区间划分，幅值采用Cover系数非等区间划分，所得8级二维载荷谱如表3所示。

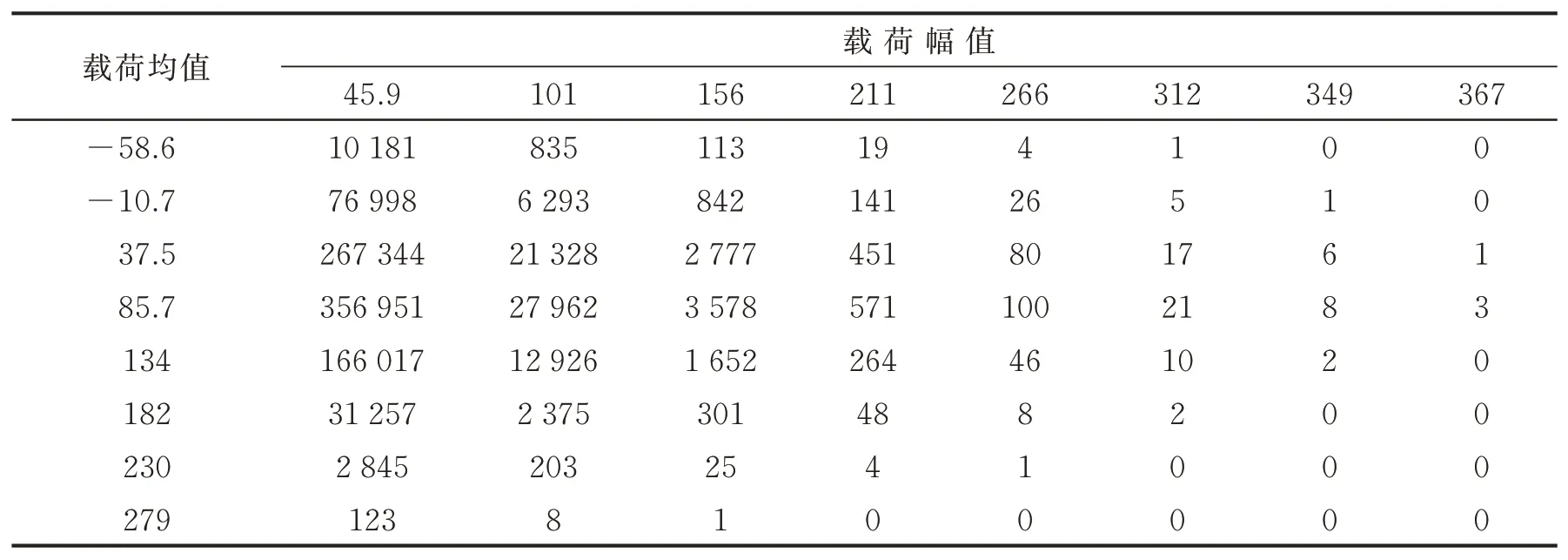
表3 参数分布估计模型所得二维载荷谱Tab.3 2‑D load spectrum based on parameter distribution kN

3 核密度估计载荷模型与载荷谱

核密度估计外载荷数据模型是利用雨流矩阵和核函数，获得对应均幅值不同分级下的载荷频次，建立外载荷数据的数学模型并编制载荷谱。工作装置当量外力如式（5）所示

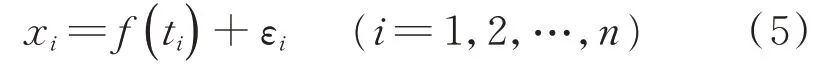
其中：xi为时刻ti时的载荷测量值；εi为随机测量误差；f（ti）为非参数模型。

对f（t）进行非参数估计，xi对f（t）的影响大小与ti和t的距离成正比，f（t）的估计应取t点的邻域内的均值加权修正值，如式（6）所示

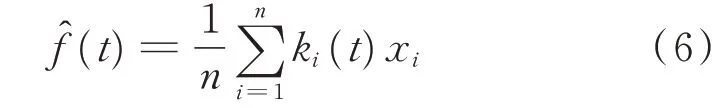
其中：ki（t）为不同时刻权重值，权重值总和为1。

用核函数g（t）代替权重函数ki（t）的方法［16］实现了非参数估计中概率密度的光滑性，避免了非连续权函数信息丢失。高斯核函数g1（t）和Epanechnikov核函数g2（t）分别如式（7）和式（8）所示

载荷数据保存为From-to形式的雨流矩阵，雨流计数得到的载荷循环与应力应变迟滞回环一一对应，所得结果不会破坏与损伤对应的应力应变迟滞回环完整结构。采用Epanechnikov核函数进行载荷数据模型建立，二维核密度估计如式（9）所示

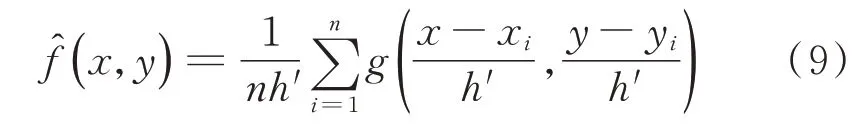
其中：n为数据个数；h'为带宽。

核函数光滑程度由其带宽决定，Epanechnikov核函数的最优带宽h'如式（10）所示

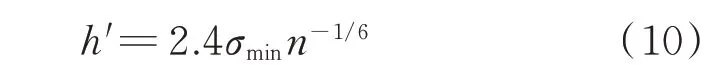
其中：σmin为二维样本标准差较小值。

装载机外载荷不同均幅值的载荷频次是动态变化的，需要确定动态最优带宽。根据随机数据点（xi，yi）引入自适应修正系数ψi如式（11）所示

将式（10），（11）代入式（9）中，得到具有自适应带宽的核密度估计数学模型如式（12）所示

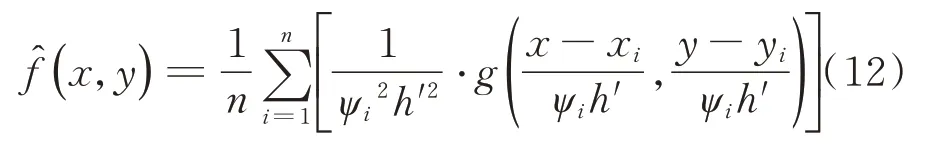
采用雨流编辑技术将图3所示4种物料的当量外载荷转化为From-to矩阵，按照表2中物料样本实测斗数和雨流频次合成为1 000斗目标样本，如图4所示。

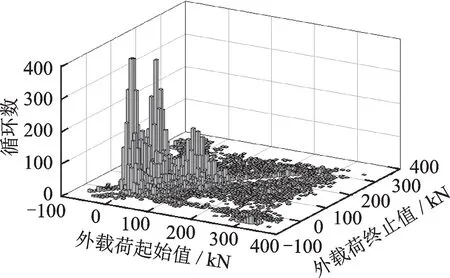
图4 不同物料合成1 000斗样本的From-to雨流矩阵Fig.4 From-to rainfall flow matrix of 1 000 bucket samples synthesized from different materials

合成目标样本数据中载荷总频次为27 570，外推至总频次106的外推倍数为36.27。根据式（12）建立核密度估计数学模型，并将外推后的From-to矩阵重构转换为Rang-mean雨流矩阵如图5所示。

得到LW900K装载机外载荷采用核密度估计模型所得8级二维载荷谱如表4所示，均值仍采用等区间划分，幅值仍采用Cover系数非等区间划分。

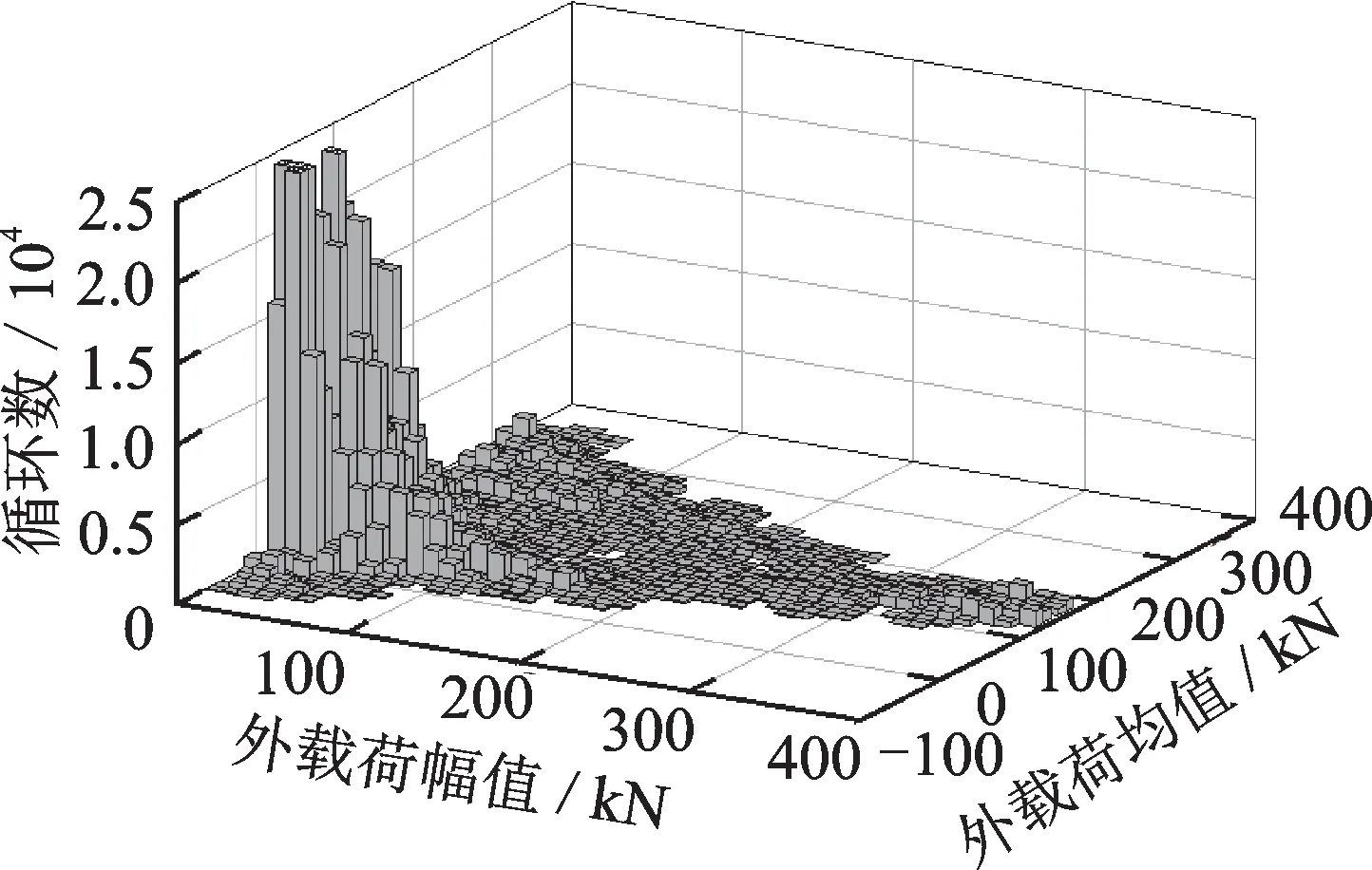
图5 核密度估计总频次106的Rang-mean雨流矩阵Fig.5 Rang-mean rainfall flow matrix with total frequency 106 estimated by kernel density

4 疲劳损伤验证试验与分析

为了验证两种载荷数据模型编制的载荷谱的合理性，按照图1所示的当量姿态载荷加载方式，搭建工作装置疲劳试验台。选择作动器施加外载荷，根据铲斗和作动器结构尺寸，确定龙门架的宽度和高度，并安装在刚性地面上。用圆形钢柱代替油缸，用刚性墙代替车架。刚性墙上安装有与动臂和钢柱连接的连接座，刚性墙固定在刚性地面上。搭建的工作装置疲劳台架实物如图6所示。

LW900K装载机动臂焊接位置主要是动臂板与横梁、铰孔衬套与动臂板处。在上述焊接大应力区域选择L-1，L-2和L-3共3个点进行载荷谱的疲劳损伤验证，如图7所示。

图6 LW900K装载机工作装置应力标定试验台Fig.6 Stress calibration test bench of LW900K loader

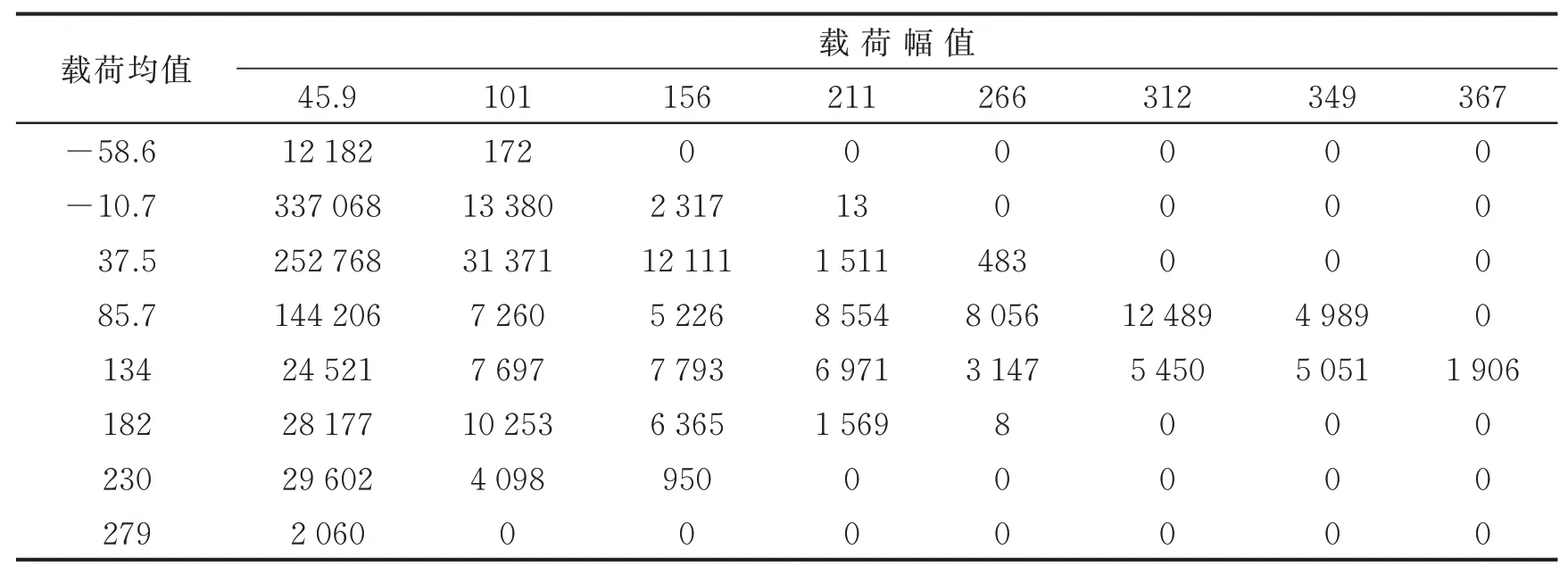
表4 核密度估计模型所得二维载荷谱Tab.4 2‑D load spectrum based on kernel density method kN

图7 疲劳损伤验证点Fig.7 Fatigue damage verification points

采用名义应力法进行疲劳损伤计算，焊接结构处在避开应力非线性增大区域后，选择焊缝应力方向上板厚2.2倍处与焊缝垂直方向的表面粘贴应变片，测得的应力作为名义应力［17］，如图8所示。

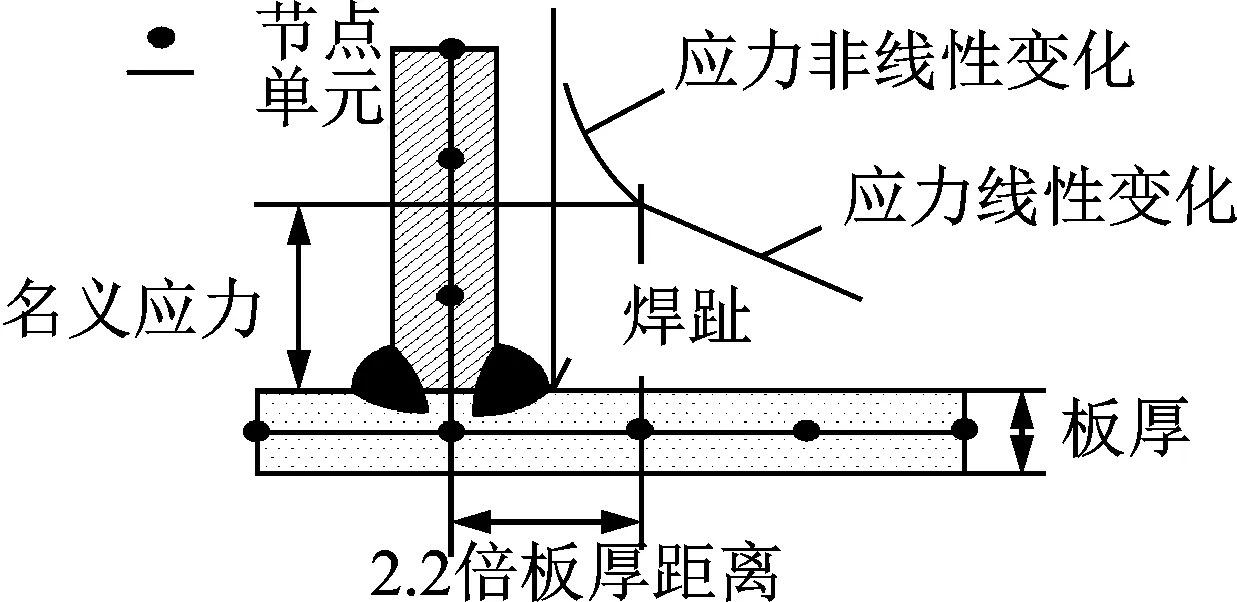
图8 焊接结构名义应力确定Fig.8 Nominal stress determination of welded structures

利用作动器多次施加200 kN的外载荷，测得结构名义应力和计算得到的传递系数如表5所示。

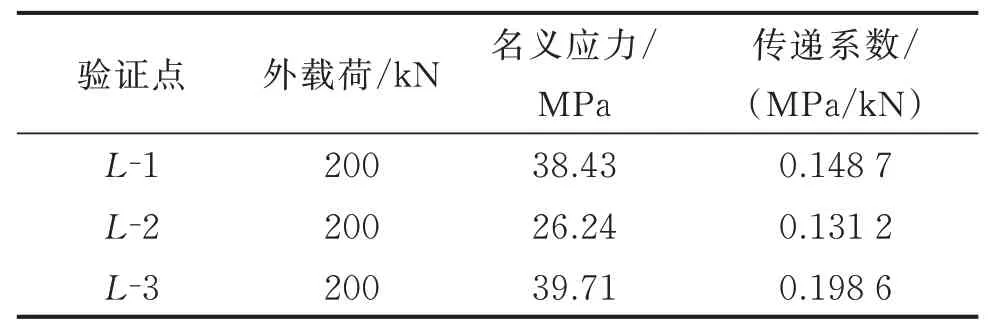
表5 疲劳损伤验证点的传递系数Tab.5 Transfer coefficients of fatigue damage verifi‑cation points

焊接结构S-N曲线在应力范围为ΔSi时疲劳损坏的循环次数Ni如式（13）所示

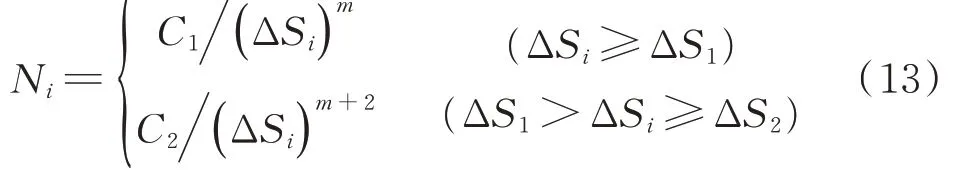
其中：ΔS1和ΔS2为焊接接头S-N曲线两个拐点对应的疲劳强度值；m取常数3；C1和C2为常数。

应力范围ΔSi的作用频次为ni时，对应的疲劳损伤Di如式（14）所示

根据验证点处焊接细部特征，选择BS7608：2014标准提供的F2等级作为疲劳损伤评估的依据，对应的疲劳损伤计算参数如表6所示。

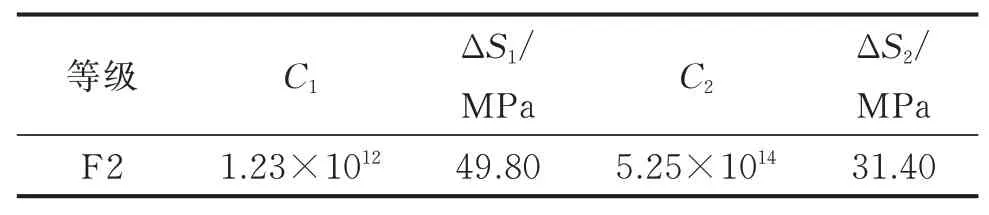
表6 BS标准计算疲劳损伤的参数值Tab.6 Parameter values for calculating fatigue dam‑age in BS standard

由参数分布估计模型中的表2和核密度估计模型中的外推倍数可知，表3和表4所示载荷谱当量装载机连续作业斗数分别为39 054斗和36 270斗。LW900K装载机完成1斗作业的平均时间为40 s，即表3和表4所示载荷谱当量装载机连续作业时间分别为434和403 h。根据表5中的传递系数将表3和表4的载荷谱转换为幅值应力频次谱，得到参数分布模型和核密度估计模型载荷谱损伤和疲劳寿命结果如表7所示。

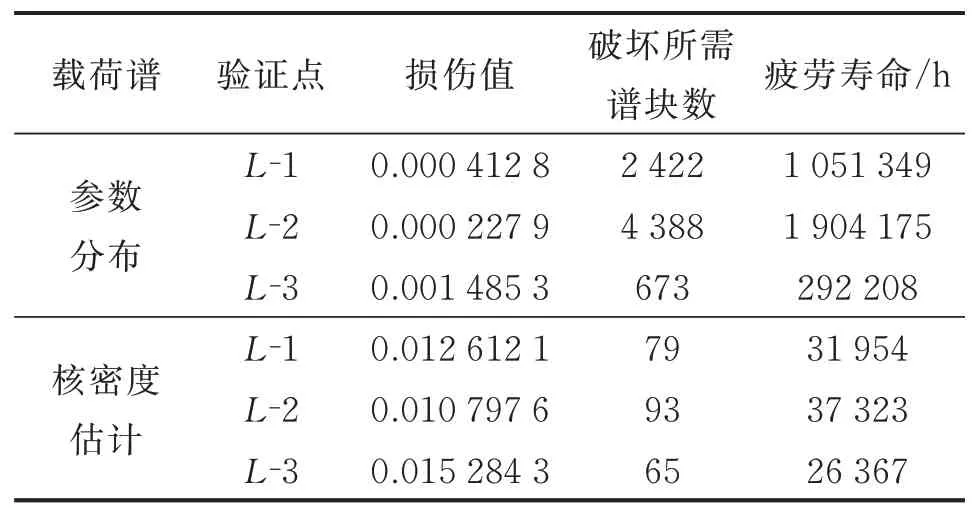
表7 载荷谱损伤计算结果Tab.7 Damage calculation results load spectrum and fatigue life results of load spectrum

由表7可知，参数分布模型获得的载荷谱损伤计算结果明显小于核密度估计模型获得的载荷谱。参数分布模型载荷谱计算的焊接结构疲劳寿命最小为29×104h，按照装载机每天24 h连续作业，至少需要33年时间才发生疲劳破坏，近似于无限寿命。核密度估计模型载荷谱计算的焊接疲劳寿命最小为2.6×104h，更接近恒幅极值载荷下的疲劳设计寿命3.0×104h。两种数据模型编制的载荷谱存在明显差异，参数分布模型所得损伤结果偏小，核密度估计模型所得损伤结果更接近实际。

通过影响疲劳损伤结果的幅值频次关系变化来分析两种数据模型编制载荷谱产生差异的原因，各物料工况实测载荷的幅值-累积频次与载荷谱编制完成后的幅值-累积频次关系变化如图9所示。

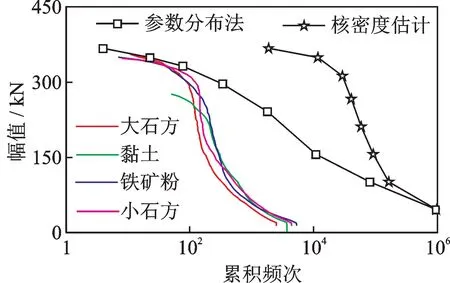
图9 幅值-累积频次关系Fig.9 Relation between amplitude range and cumulative frequency

两种数据模型编制的载荷谱都实现了载荷幅值和频次的双向外推扩展，参数分布估计数据模型编制的载荷谱中幅值-累积频次在大载荷区域内的载荷频次数没有得到扩展反而降低了，这是由于样本中的小载荷循环频次多，对均幅值载荷分布拟合参数的结果影响大。虽然载荷分布拟合满足检验要求，但是参数分布规律对小载荷的拟合度要明显高于大载荷，幅值较小的载荷频数大，对载荷统计分布影响权重高，使得满足一定可靠度的分布并不能完全反应载荷雨流计数中均幅值频次谱形，在幅值载荷分布拟合中体现的尤为明显。

核密度估计模型以雨流矩阵为基础，具有自适应带宽特性的二维核密度函数与工作装置当量外载荷均幅值同步对应。疲劳损伤验证试验结果表明，在进行装载机疲劳试验载荷谱编制时核密度估计数据模型无需假定载荷均值和幅值的分布类型，所得载荷谱的幅值-累积频次关系曲线实现了对大载荷和小载荷的同步频次扩展，核密度估计模型获得的载荷谱结果能够弥补参数分布模型中分布拟合对低频数大载荷影响弱化的不足。

5 结束语

核密度估计模型和参数分布模型都能够获取工作装置载荷谱，疲劳损伤验证试验结果表明，参数分布模型载荷谱损伤结果明显偏小，核密度估计模型载荷谱损伤结果计算得到的焊接位置处的疲劳寿命更接近疲劳设计寿命3×104h；核密度估计模型以雨流矩阵为基础，具有自适应带宽特性的二维核密度函数与工作装置当量外载荷均幅值同步对应，所得载荷谱结果能够弥补参数分布模型中分布拟合对低频次的大载荷影响弱化的不足，且无需对样本做分布假设；建立的参数分布估计和核密度估计数据模型以及编制的载荷谱为装载机结构件的疲劳可靠性分析提供关键依据。下一步将开展装载机结构件疲劳寿命预测和试验研究。