多排耦合变速机构振动特性建模与试验

张 强，许 晋，李洪武，张玉东

（中国北方车辆研究所车辆传动重点实验室 北京，100072）

引言

高速履带车辆要求在复杂多变的外界环境中实现快速部署、快速机动，行星变速机构是实现其灵活性与机动性的核心部件［1］。行星变速机构内部通常由3～4个行星齿轮组构成，通过操纵件对不同行星齿轮组的操控，实现车辆转向、加速、制动等功能［2］。行星变速机构振动加剧会降低车辆的使用寿命，且有可能与发动机等外部激励发生共振，对履带车辆上其他设备的使用造成影响，也会使得履带车辆驾驶人员出现不良反应，从而影响其使用功能的发挥［3］。但是因多排行星变速机构的结构复杂且不同排之间存在耦合作用，导致内部行星排啮合过程与其振动的映射关系仍不清楚［4］。因此，对行星变速机构振动特性的深入研究，从而实现行星变速机构的动力学特性的优化设计，具有重要的理论意义及工程应用价值［5］。

针对行星变速机构的振动特性问题，Parker等［6］利用接触力学和有限元模型，分析具有齿侧间隙和时变刚度的齿轮副的动态响应，并研究了齿轮的接触冲击、齿间载荷分布及齿廓修型。Kahrarman［7］通过建立行星轮系的纯扭转振动模型，研究了行星轮系的固有频率及自由振动特性。张锁怀等［8］建立了4自由度的齿轮系统动力学模型，该模型了考虑齿侧间隙的影响，采用数值仿真求解系统的不平衡响应，但是该模型中假设主动齿轮轴为刚性轴。Sellgren等［9］运用有限元法，研究了齿轮箱动态响应，分析了模型中不同的轴承的刚度及连接形式对动态响应的影响，并分析了工况条件、齿轮啮合、箱体结构刚度对齿轮系统振动特性的影响。Riguad等［10］猜测变速箱产生振动噪声的主要原因是齿轮在加工制造过程中产生的误差，并对该假设进行了验证。Liu等［11］建立了考虑行星轮轴承内部激励的船用行星轮系有限元模型，研究了行星轮轴承内部激励对系统动态响应特性的影响规律。

国内外研究机构虽然对行星变速机构振动特性进行了大量的研究［12-13］，但研究内容仅限于简单行星排及小功率变速机构振动测试，对于高速履带车辆使用的大功率多排耦合行星变速机构，由于振动建模分析复杂，振动数据测量困难，因此建模及试验研究均较少［14］。针对这一问题，基于第2类拉格朗日方程，推导了行星变速机构“平动-转动”耦合激励振动动力学模型，研究了典型工况下行星变速机构的时域和频域振动特征，并将仿真结果与试验测得的行星变速机构的振动特性进行对比分析，验证了“平动-转动”耦合模型及其计算结果的正确性。

1 行星变速机构设计方案及测试系统

1.1 行星变速机构设计方案

依据图1行星变速机构的设计方案，该行星变速机构行星轮系包含3个行星排和6个换挡元件，换挡元件包括3个离合器（C1，C2，C3）、3个制动器（B1，B2，B3），可以实现7种挡位，方案简图如图1所示。

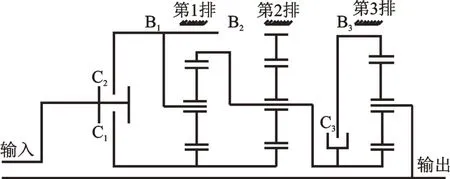
图1 行星变速机构方案简图Fig.1 Schematic diagram of the gearshift mechanism

该行星变速机构具体换挡逻辑见表1，其中“○”表示闭合。1挡时的换挡逻辑见表1中第1行，在1挡时制动器B1，B3与离合器C1闭合，其他换挡原件分离。表1中第2行表示2挡时，制动器B3与C1，C2闭合，其他换挡元件分离。

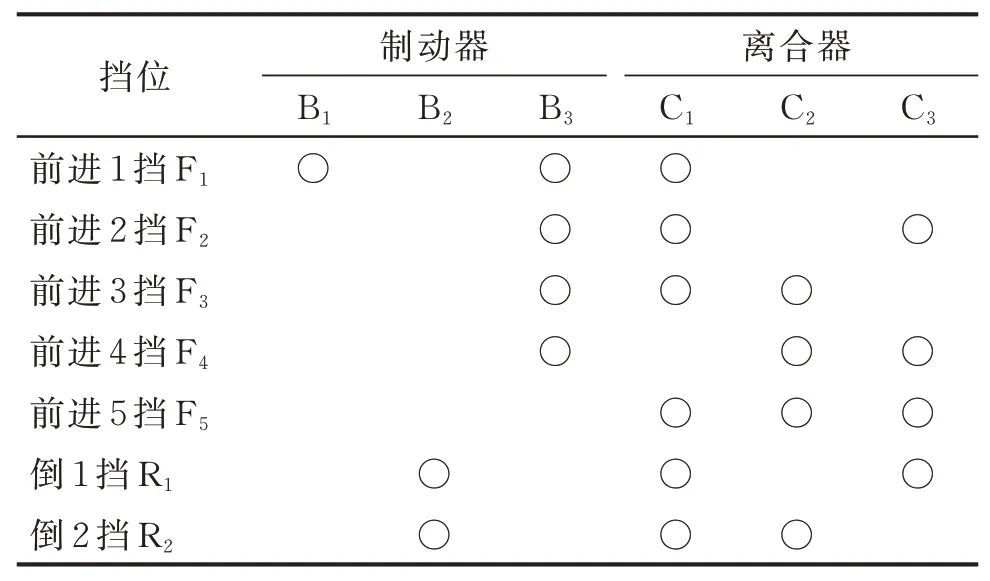
表1 行星变速机构换挡逻辑表Tab.1 Shift logical of gearshift mechanism

1.2 行星变速机构轮系参数

该行星变速机构由3个简单排组成，具体3个行星排齿轮的参数见表2。3排行星齿轮的模数均为4，压力角均为25°，齿顶高系数为1，径向间隙系数为0.2，齿根圆角半径系数为0.25。

1.3 行星变速机构振动测试系统

行星变速机构振动加速度试验测试系统如图2所示，该系统由增速箱、驱动电机、加载电机和行星变速机构包箱等构成，试验台采用驱动电机实现行星变速机构的驱动，用测功机实现加载。在测试过程中，该试验系统可以实时采集转矩、振动加速度、操纵油压及转速等数据。

1.4 行星变速机构振动测试设备及测点布置

试验系统测点布置如图3所示，分别在输入端和输出端安装2个测点，并对其x和y方向的振动加速度进行测量，其中，x方向为垂直振动加速度，y方向为平行振动加速度。图中5#和6#为输出端安装传感器位置，7#和8#为输入端安装传感器位置。

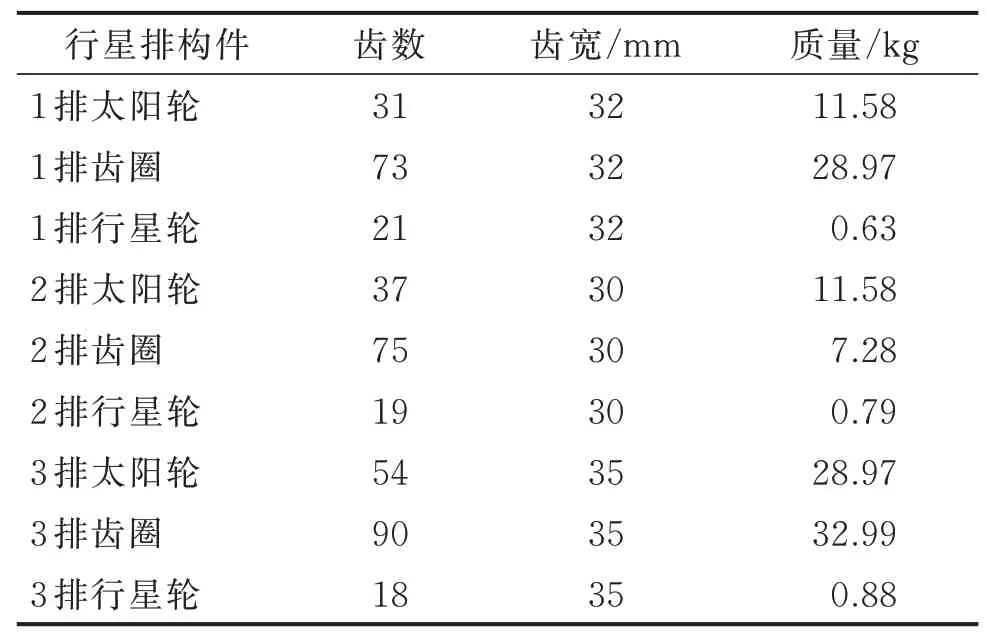
表2 行星变速机构各排齿轮参数Tab.2 Gear parameters of each row of gearshift mechanism

图2 行星变速机构振动加速度试验测试系统Fig.2 Vibration acceleration test system for gearshift mechanism

图3 振动加速度测点布置Fig.3 Vibration acceleration measuring layout

2 行星变速机构振动模型的建立

2.1 基本参数系统运动学分析

根据行星变速机构的各排齿轮参数，通过运动学关系计算可以得到各挡旋转构件频率，1挡时旋转构件的频率见表3。

2.2 振动仿真数学模型

基于第2类拉格朗日方程，推导了行星齿轮“平动-转动”集中质量耦合振动动力学运动微分方程，行星变速机构的集中质量模型中的单排行星轮动力学模型如图4所示。图4中：φ为太阳轮与行星轮位置角度；l，r，c，s分别为行星轮、齿圈、行星架和太阳轮；u为旋转位移；kry，kcy，ksy分别为齿圈、行星架和太阳轮在y方向的支撑刚度；krx，ksx分别为齿圈和太阳轮在x方向的支撑刚度；krt，kst分别为齿圈和太阳轮的扭转刚度；krl1，ksl1分别为第1个行星轮和齿圈及太阳轮的啮合刚度，krl2，ksl2分别为第2个行星轮和齿圈及太阳轮的啮合刚度；klpx，klpy分别为行星轮在x和y方向上的支撑刚度。

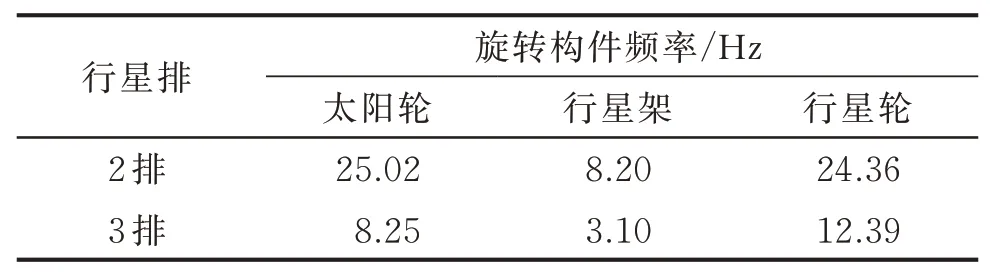
表3 1挡旋转构件频率Tab.3 Frequency of rotating component in first gear

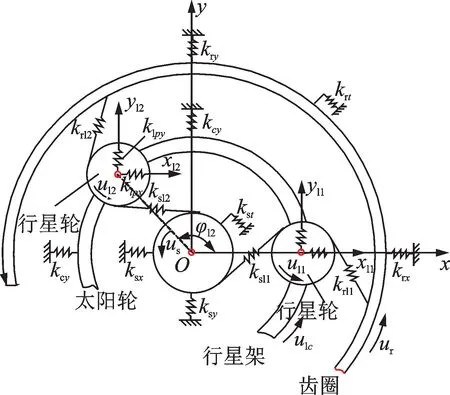
图4 单排行星轮动力学模型Fig.4 Dynamic model of single row planetary gear

由于行星轮系包含3个行星排和7种挡位，为方便计算，建立了通用的多排耦合行星轮系动力学模型，其关系图如图5所示。图中：Krc1为第1排齿圈和行星架之间的刚度；Kss1为第1排太阳轮之间的刚度；Kcs2为第2排行星架和太阳轮之间的刚度。

图5 多排行星轮系耦合关系图Fig.5 Coupling diagram of multi-row planetary gear trains

行星轮与太阳轮、齿圈啮合关系如图6所示，其中：k为构件间刚度；e为啮合误差；φ为太阳轮与行星轮位置角度；xs和ys分别为太阳轮在x方向和y方向的位移；xn和yn则为第n个行星轮在x方向和y方向 的 位移；kct为行星 架 的扭转刚 度；ksn，krn为第n个行星轮和太阳轮、齿圈之间的啮合刚度；esn，ern为第n个行星轮和太阳轮、齿圈之间的啮合误差。

图6 行星轮与太阳轮、齿圈啮合关系图Fig.6 Engagement relationship between planetary gear,solar gear and gear ring

多排耦合行星轮系动力学模型的运动方程的表达式为

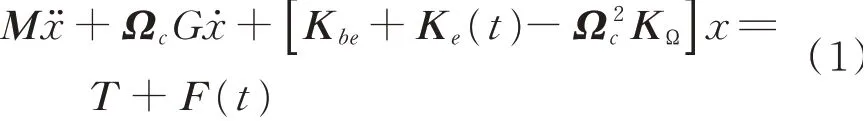
其中：M为质量矩阵；Kbe为支承刚度矩阵；T为外部激励力矩阵；Ωc为角速度矩阵；G为陀螺矩阵；Ke（t）为啮合刚度矩阵；F（t）为轮系内部激励力矩阵。

广义位移矢量为

其中：上标i（i=1，2，3）为第i排行星轮系；r，c，s分别为齿圈，行星架和太阳轮；1，2，…，n表示第n个行星 轮；x和y分别为构件在x和y方 向的位 移；θ为构件在圆周方向的旋转位移。

建立固定坐标系，则

太阳轮线位移沿啮合线方向的x，y以及旋转方向的位移投影为其中：ω为构件的角速度；ris为第i排太阳轮的基圆半径。

行星轮线位移沿啮合线方向的x，y以及旋转方向 的 位 移 投 影 为其中为第i排第n个行星轮圆周方向位移。

太阳轮相对于行星轮沿啮合线上的投影差为

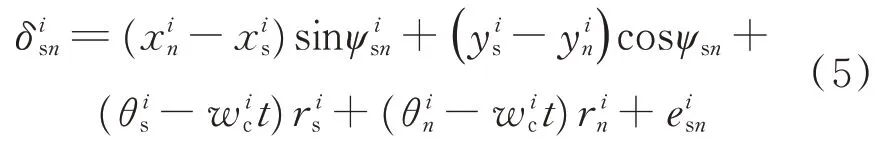
齿圈线位移沿啮合线方向的x，y以及旋转方向的 位 移 投 影 为和

行星轮线位移沿啮合线方向的x，y以及旋转方向的位移投影为

行星轮相对于齿圈沿啮合线上的投影差为

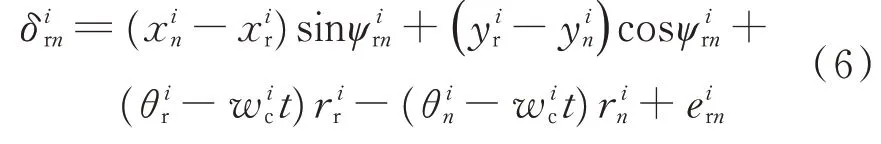
行星架与行星轮的相对位移为

行星架运动方程为

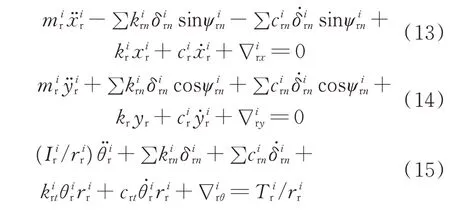
太阳轮运动方程为

行星轮运动方程为

3 仿真模型与试验分析数据对比

采用Runge-Kutta法，求解行星变速机构的动力学响应，可得太阳轮、每个行星轮和齿圈平动加速度、位移、速度、转动加速度、位移、速度的幅值A、频率f和相位φ等信息。以下对该行星变速机构的典型工况第1挡转速1 500 r/min和扭矩1 093 N/m条件下输入输出构件的运动状态进行分析。

3.1 振动时域仿真与试验对比

该行星变速机构在1档1 500 r/min和扭矩1 093 N/m条件下输入x方向加速度时域图如图7所示。

仿真结果显示，1挡时输入构件x方向仿真分析加速度均方根（root mean square，简称RMS）值为0.652 2g，试验测得输入构件x方向加速度RMS值为0.676 2g，理论试验测试值与理论分析值相差3.68%。

1挡输入构件仿真分析获得的y方向加速度的RMS值为0.672 7g，试验获得y方向加速度的RMS值为0.655 3g。仿真分析值与试验测试值相差－2.59%。对于输入构件，仿真分析获得x方向和y方向加速度的RMS值相差-3.09%，试验测试值x方向和y方向加速度的RMS值相差3.14%。结果表明，输入构件x和y方向振动加速度的RMS值相差较小。

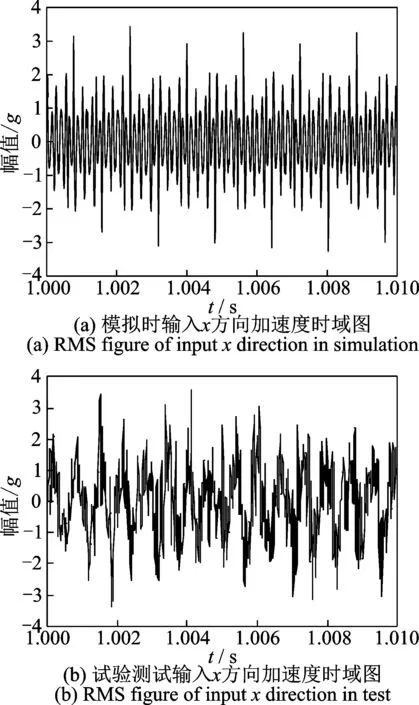
图7 模拟和测试输入x方向加速度时域图Fig.7 RMS figure of input x direction in simulation and test

该行星变速机构在典型工况下输出x方向加速度时域图如图8所示。仿真结果显示，1挡输出构件仿真分析获得的x方向加速度的RMS值为2.099g，试验测得x方向加速度的RMS值为1.84g。仿真分析值与试验测试值相差－12.3%。1挡输出构件仿真分析获得的y方向加速度的RMS值为2.108g，试验测试y方向加速度的RMS值为2.439g。仿真分析值与试验测试值相差13.6%。

对于输入端与输出端加速度的RMS值，输出构件x方向上试验测试值是输入构件的2.72倍，输出构件y方向上试验测试值是输入构件的3.72倍，仿真和分析结果表明，输出端RMS值远大于输入端。

3.2 振动频域仿真与试验对比

在1挡转速1 500 r/min和扭矩1 093 N/m工况下输入构件x方向仿真分析与试验测得加速度频域如图9所示。通过1挡输入构件x方向加速度频域理论分析与试验分析比较，可以得到各阶频率幅值对比结果，具体值如表4所示。

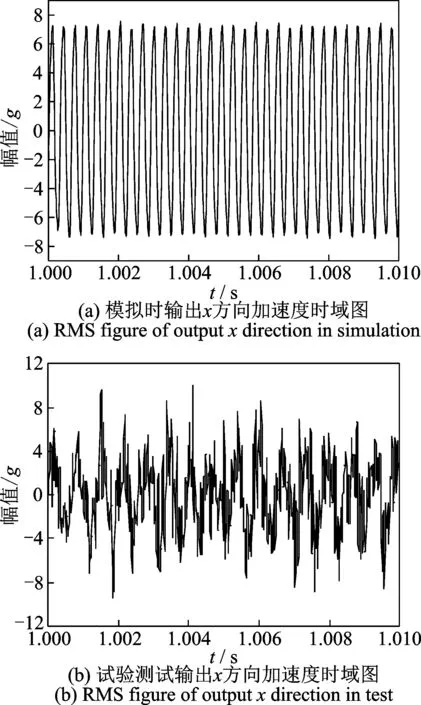
图8 模拟和测试输出x方向加速度时域图Fig.8 RMS figure of output x direction in simulation and test

仿真分析获得的输入构件x方向的第1个波峰频率值为622.6 Hz，经试验测得的第1个波峰频率为627.7 Hz，对比表3中1挡旋转构件的频率，可以得出第1个波峰为第2排行星排太阳轮与行星轮啮频。仿真值第2个波峰为1 233 Hz，振动测试频域值的第2个波峰为1 222 Hz，第2排行星排太阳轮与行星轮啮频的2倍频频率为1 238.8 Hz，与第2个波峰吻合。

对比其余波峰值，其第3～6个波峰均对应于第2排行星排太阳轮与行星轮啮频的倍频处，分别对应着3倍值6倍频。1挡输入构件y方向上的频域值与x方向上类似，其仿真及测试获得的振动波峰峰值均一致。

通过对输入构件x方向的频域仿真分析与测试分析的比较，得出其频域值仿真与测试结果一致，其频域的波峰的峰值主要为第2排行星排太阳轮与行星轮的啮频及倍频处，此处为产生的振动值最大。

1挡输出构件在典型工况下x方向仿真分析与试验测得加速度频域如图10所示。1挡输出构件x方向加速度频域理论分析与试验分析比较结果如表5所示。仿真分析获得的输出构件x方向的第1个波峰频率值为562.4 Hz，经试验测得的第1个波峰频率为561.5 Hz，对比表3中1挡旋转构件的频率，可以得出第1个波峰为第3排行星排太阳轮与行星轮2倍频，2倍频的理论频率为560.2 Hz。仿真分析第2个波峰为842.4 Hz，振动测试频域值的第2个波峰为843.3 Hz，第3排行星排太阳轮与行星轮啮频的3倍频频率为840.3 Hz，与第2个波峰吻合。

图9 模拟和测试输入x方向加速度频域图Fig.9 Frequency domain figure of input x direction in simulation and test

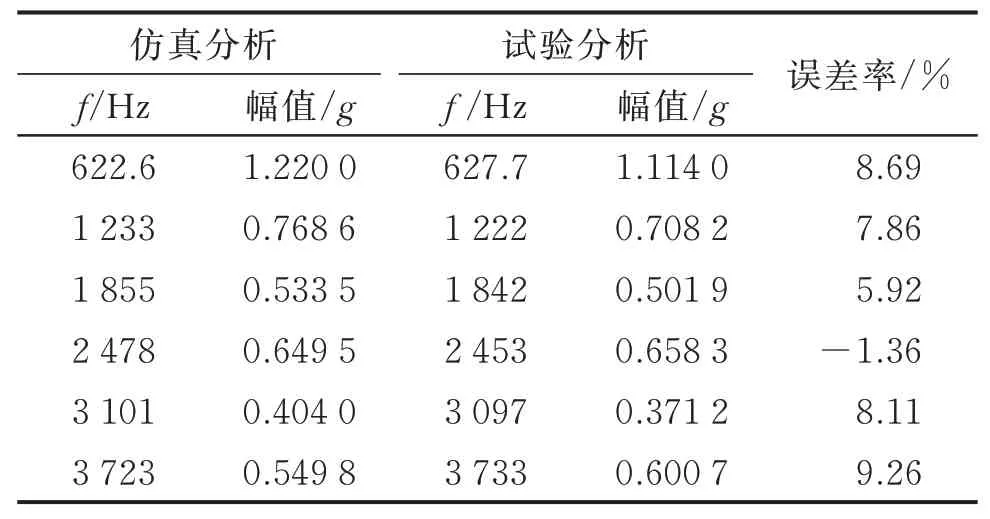
表4 输入构件x方向加速度频域模拟与试验对比Tab.4 Frequency domain of input x in simulation and test

对比其余波峰值，其第3～10个波峰均对应于3排行星排太阳轮与行星轮啮频的倍频处，分别对应着4倍值11倍频。1挡输出构件y方向上的频域值与x方向上类似，仿真及测试获得的振动波峰峰值均一致。输入构件x方向的频域仿真分析与测试对比分析结果显示，其频域值仿真与测试结果一致，频域波峰的峰值主要为第2排行星排太阳轮与行星轮的啮频及倍频处，此处为产生的振动值最大。输出构件x方向的频域仿真分析与测试结果对比分析显示，其频域的波峰值主要为第3排行星排太阳与行星轮的啮频及倍频处。

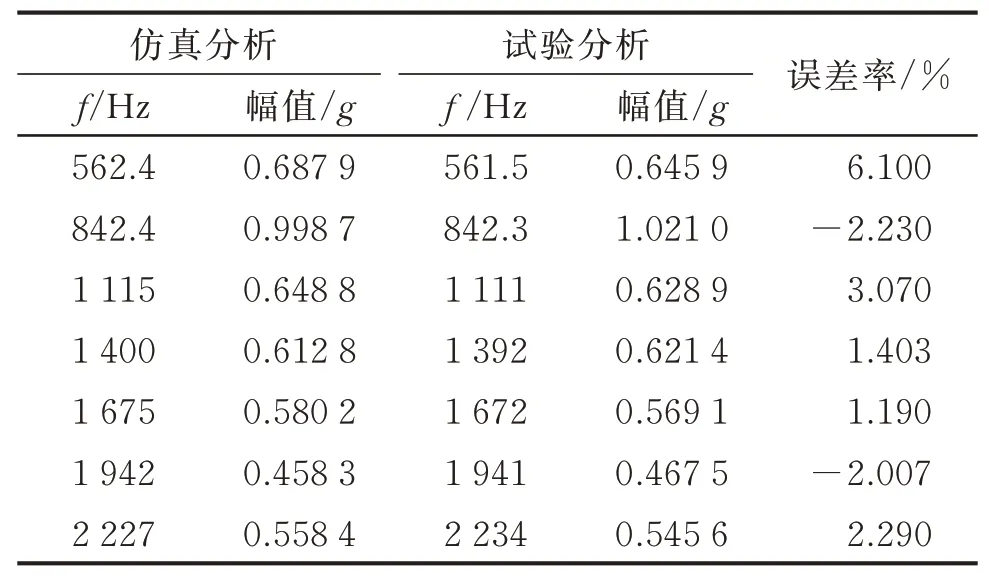
表5 输入构件y方向加速度频域理论与试验对比Tab.5 Frequency domain of input y in simulation and test

输出及输出端频域值结果显示，在一挡下，振动的最大值为第2排及第3排行星轮与太阳轮的啮频及倍频处，针对此问题，可以通过行星轮及太阳轮修型，减少传递误差，提高齿轮加工精度等手段降低其振动。通过振动特性的仿真与试验分析，为行星排的振动优化设计指明了具体的方向。

4 结束语

基于第2类拉格朗日方程，推导获得了多排耦合行星齿轮“平动-转动”耦合振动动力学模型，运用Runge-Kutta法，求解系统动力学响应。通过搭建行星变速机构振动测试系统，对行星变速机构振动加速度数据进行采集，并将建模仿真与试验测得的振动特性进行对比，对典型工况输入输出构件的振动状态进行分析，研究了行星变速机构建模仿真与试验测试下时域、频域等特性。结果表明：①输入和输出构件x和y方向加速度时域仿真值与试验测试值吻合，且输入端或输出端x和y方向上的RMS值相差较小，但输出端RMS值远大于输入端；②输入和输出构件频域仿真值与试验测试值也一致，其振动能量主要集中于第2排及第3排行星轮与太阳轮啮合的啮频及倍频处；③通过行星变速机构振动特性建模与试验对比分析，验证了多排耦合行星齿轮“平动-转动”振动动力学模型的准确性，为行星变速机构的动力学设计优化提供了理论参考。