基于数据挖掘与信息融合的制冷设备故障诊断∗

周旖鋆，武 凯，孙 宇，杨晓燕，楼晓华

（1.南京理工大学机械工程学院 南京，210094） （2.南通四方科技集团股份有限公司 南通，226300）

引言

制冷设备几种故障同时发生时，各单发故障间会相互影响、相互诱导、相互耦合，增加故障诊断系统的误报率和漏报率。因此，开展制冷设备并发故障的诊断具有重要的应用价值。Macalister等［1］基于图论建立了制冷设备的故障诊断模型，但这种模型面对较为复杂的系统时可能给出无效诊断结果。Salvatore等［2］将专家经验的知识库与推理机制相结合对制冷设备故障进行诊断，但这类方法推理过程中存在匹配冲突等问题。Flore等［3］基于主元分析方法在制冷设备故障检测中建立主元模型，通过对比测量数据与正常数据的统计量判断制冷设备是否发生故障，然而这种诊断方法只能执行单一故障诊断。Kumar［4］基于指定元分析（designated cell analysis，简称DCA）方法对制冷系统故障进行了诊断，但由于DCA方法仅在各特征向量相互正交的情况适用，因此当用于并发故障诊断时，诊断结果不够准确。韩 华 等［5］把 支 持 向 量 机（support vector machines，简称SVM）模型用于制冷设备故障诊断研究并得到了较为准确的诊断结果。

为准确检测出制冷设备的并发故障，提出一种基于数据挖掘与信息融合的并发故障诊断方法。首先，采集设备正常工况数据和各类单发故障与并发故障下的数据，并分别建立指定元分析模型和支持向量机模型，为了使指定元分析方法适用于非正交模式，对原来的算法进行改良，提出非完全正交指定元分析方法（non-fully orthogonal designated cell analysis，简称NFODCA）；其次，采用上述两种数据挖掘方法诊断制冷设备故障并进行实验验证；最后，采用加权证据理论对两种方法的诊断结果进行信息融合以提高诊断结果的可信度。

1 故障数据获取

制冷设备可能产生的故障类型较多，根据经验知识对制冷系统的工作原理进入深入分析后，选取了6类较为典型的单发故障，通过故障随机组合形成并发故障进行研究，所选取的6类典型故障如下：①压缩机的吸排气阀片受损，当这类故障发生时，压缩机的实际输气量下降，制冷效果降低；②制冷剂不足，制冷剂短缺的原因通常有两个，一种是制冷剂在出厂前充注不足，另一种是由于阀门或焊点松动导致的制冷剂泄漏；③循环水泵不转，这种故障会造成压缩机吸排气温度迅速上升，同时冷凝器的冷却效果也会急剧下降；④冷却水的流量太小，冷却塔的水垢太大或冷却塔内部布置不当可能导致冷却水流量太小；⑤膨胀阀开度过小，当这种故障发生时会造成制冷设备循环的制冷剂不足；⑥过滤器堵塞，过滤网用于过滤灰尘和金属碎屑等，使用时间过长易被堵住。

实验对象为一台需配冷量为55 kW的制冷机组，在原有设备基础上引入制冷设备故障模拟及参数测试组件，通过实验采集故障数据。各故障的实现方法如下：①压缩机吸排气阀片损坏，在压缩机吸、排气管路之间设旁通通路，并安装针阀或计量阀作为旁通量调节装置；②制冷剂不足，先将系统抽真空，然后通过逐步加注实现不同程度制冷剂不足的故障模拟；③循环水泵不转，断开水泵控制电路即可模拟循环水泵不转的故障；④冷却水流量过小，降低旁通流量或减少冷却水闸阀开度均可改变冷却水量；⑤膨胀阀开度过小，将手动调节阀置于电磁阀与蒸发器之间以模拟膨胀阀开度过小；⑥过滤器堵塞，将一定比例的滤网面积用均布孔洞的厚纸挡住可以模拟过滤器堵塞引起的故障。故障模拟及参数测试组件安装位置如图1所示。

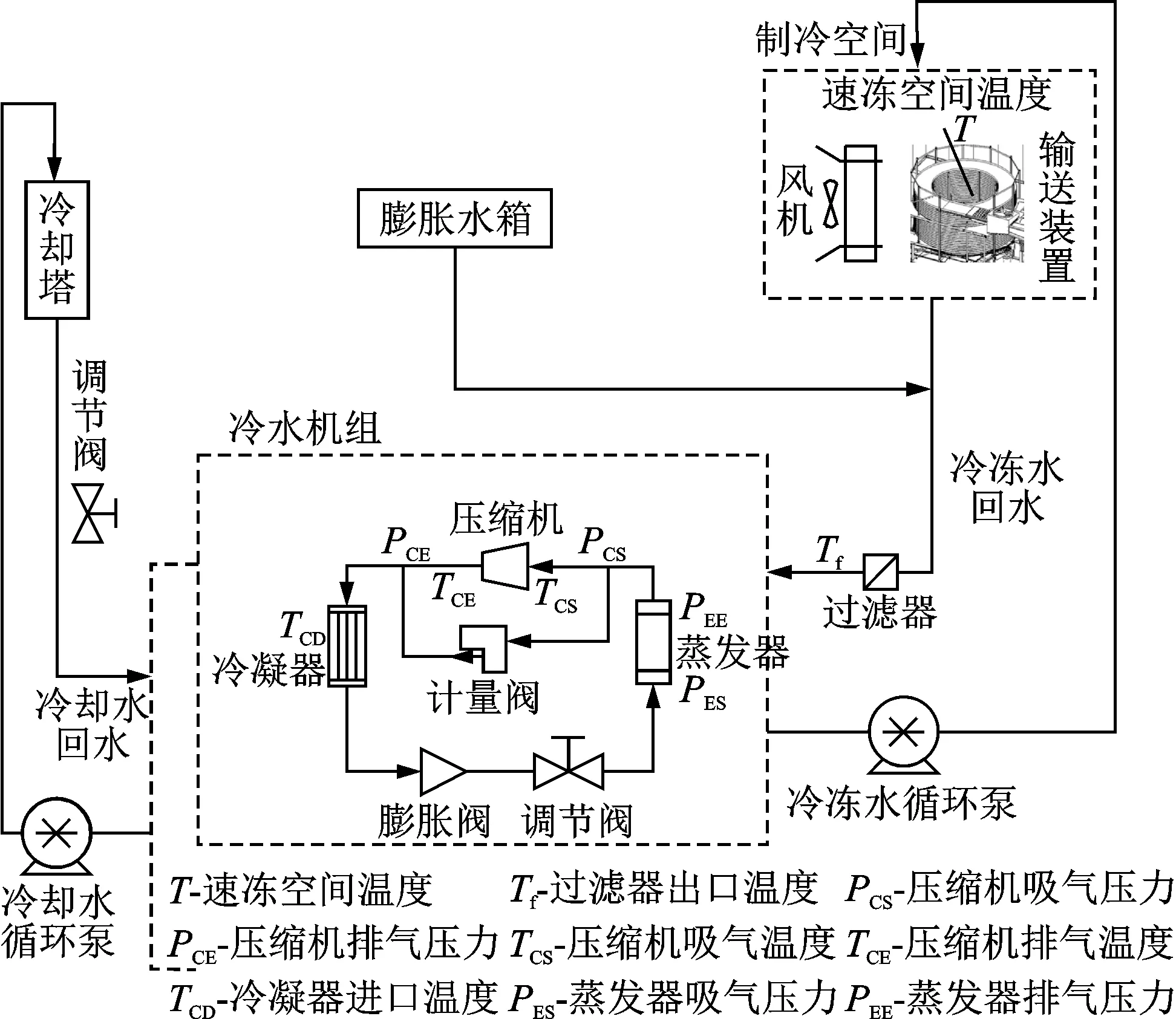
图1 故障模拟及参数测试组件安装位置Fig.1 Fault simulation and parameter test component installation location

2 非完全正交指定元分析

2.1 非完全正交指定元分析模型建立

由于NFODCA模型在建立时无需并发故障数据作为训练集，仅在验证模型阶段需要并发故障的数据。因此，将2/3的单发故障数据和2/3正常工况数据作为训练集用于模型建立，将并发故障数据、剩下的1/3类单发故障数据和1/3正常工况数据作为测试集用于模型验证。

制冷设备的故障现象、故障原因之间的关系可以用故障征兆集描述，征兆用测量值与标称值的偏差度表示。根据实际运行经验和论证分析，在制冷设备系统运行过程中对压缩机吸气压力上升、冷凝器进口温度上升等12种征兆进行监测，则每种征兆ur(r=1，2，…，12)可表示为

将故障种类的数目记为s，则s种故障Ds可定义为论域U中的6种指定模式

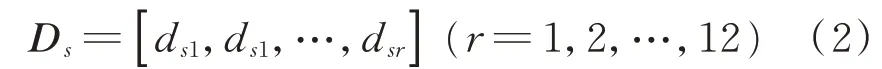
其中

选取6种单发故障：压缩机吸排气阀片损坏d1、制冷剂不足d2、循环水泵不转d3、冷却水流量过小d4、膨胀阀开度过小d5、过滤器堵塞d6；2种单发故障组合成的7类并发故障：d7=d1+d3，d8=d1+d6，d9=d2+d5，d10=d3+d4，d11=d3+d6，d12=d4+d5，d13=d5+d6；3种 单 发 故 障 组 合 而成的3类并发故障d14=d1+d2+d4，d15=d3+d4+d6，d16=d4+d5+d6共 计16种 故 障 和 正 常工况进行实验数据采集。以上故障类型根据经验知识结合实际工况选出，其他类型的单发故障及其他组合形成的并发故障也可采用文中所述的研究方法。

把故障征兆定义为压缩机排气压力上升u1、下降u2，压缩机吸气压力上升u3、下降u4，压缩机排气温度上升u5、下降u6，压缩机吸气温度上升u7、下降u8，冷凝器出口温度上升u9、下降u10，过滤器温度上升u11、下降u12，分析实验结果可得故障与征兆间关系如表1所示。

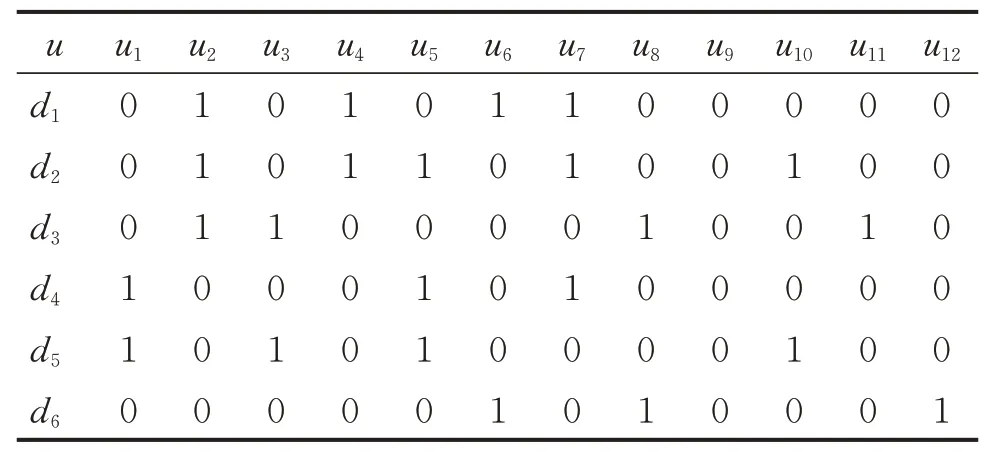
表1 制冷装置故障与征兆间关系Tab.1 The relationship between faults and symptoms of this quick freezing device

由表1可知，按照式（2）定义的故障模式并非全部正交，例如：发生压缩机吸气阀片损坏时会导致压缩机吸气压力下降，而发生循环水泵不转的故障时会间接导致压缩机吸气压力上升；当这两种故障同时发生时，二者的故障特征会相互影响甚至抵消，而传统指定元分析算法仅在正交模式下适用；这两种不相互正交的故障同时发生时，将造成故障漏报。所以对传统指定元分析方法进行改良，使之适用于非完全正交模式。

当样本数据Y处于完全正交模式时，Y具有指定元的分解式［6］

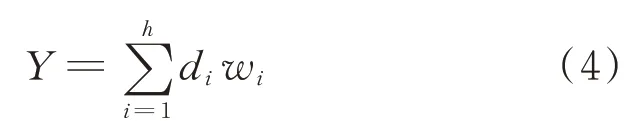
其中：Y由正常子空间和故障子空间组成；di为正交指定模式；wi为相应指定元。

当Y处于非完全正交模式时可以表示为

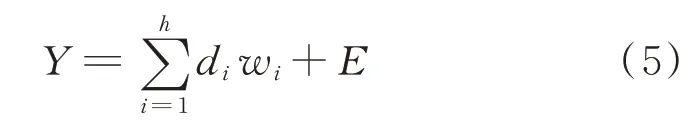
其中：E为残差空间。

以EET最小为原则将指定模式集划分为m个组内正交的子集，样本数据Y就可以表示为组内正交子集与残差阵的和

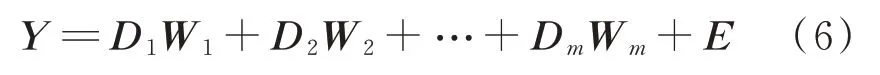
各子集指定元显著性可用式（7）计算得出

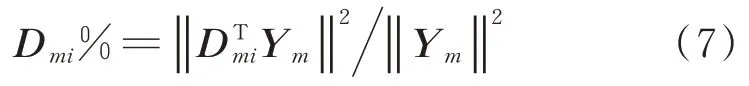
在指定模式di所表示方向上用式（8）将样本数据Y做投影，即可得到相应的指定元wi

其中：n为样本数量。

例如：[y11，y21，…，ym1]T表示第1组样本数据第m个指定模式下的特征向量。计算得到的win表示第i个指定元下第n个样本所对应的映射值，组成如下的特征向量

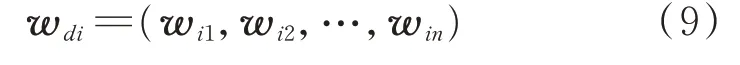
最后，根据正常工况下的数据计算出每个指定元对应特征值的控制上下限并得到Shewhart图，若图中特征值超过了控制限，则认为制冷设备发生了相应故障。

2.2 实例验证

从测试集中随机选取实验数据，用NFODCA模型进行故障诊断，并将诊断结果与故障模拟实验所采集数据的故障记录对比，验证模型的可靠性。

根据表1中的制冷装置故障与征兆间关系和EET最小原则，将非完全正交的模式集D={d1，d2，…，d6}表示成3组组内正交的模式子集，根据式（6），样本数据Y可以表示为

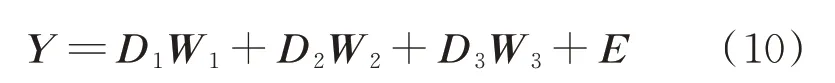
即当非完全正交模式集D划分为3个组内相互正交的模式子集时，Y可由各投影空间完全表示。

随机选取一组实验数据，分别关于D1，D2，D3做指定元分析，根据式（7）计算出该组数据对应的各个指定模式的显著性如表2所示。

表2 对应各指定模式的显著性Tab.2 Corresponding to the saliency of each desig‑nated mode

从表2可以看出，该组数据对应的6种指定模式中，d1，d4，d6对系统的影响较大，据此可以初步判断系统中可能发生了压缩机吸排气阀片损坏、冷却水流量过小、过滤器堵塞三种故障。为了进一步验证该方法的合理性，根据正常工况数据在置信度为95%的条件下计算出各个指定模式d1的控制下限L1及上限U1为

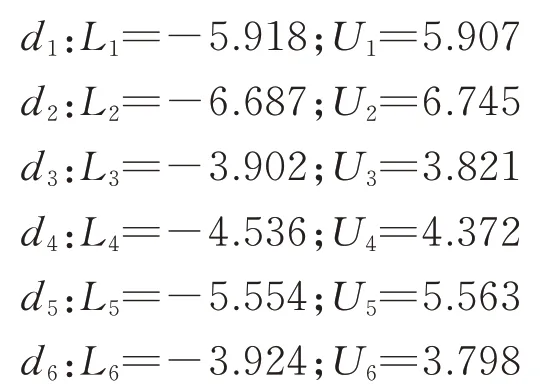
将Y在所有指定元上进行投影，根据上文计算出的控制限在图2中给出各指定元的Shewhart图，图中U，L分别为控制上、下限，横坐标为样本编号，纵坐标表示由式（8），（9）得出的第i个指定元下第n个样本所对应映射值组成的特征向量的特征值，该量无单位。

从 图2可 以 看 出，第1，4，6个 指 定 元 的Shewhart图在第270个采样点以后超出了控制限，而第2，3，5个指定元的特征值仍稳定在控制限以内，证明制冷设备从第270个点开始出现了d1，d4，d63种类型的故障。

将故障诊断结果与故障模拟实验采集数据的故障记录对比，结果表明，诊断结果与采集数据时的记录一致。同理可得到其他测试集数据经NFODCA模型分析后的诊断结果，并与故障模拟实验采集数据的故障记录对比，最终得出NFODCA模型的故障诊断准确率为96.94%，虚警率为0.48%，证明文中提出的非完全正交指定元分析方法能准确判断制冷设备的并发故障，是一种有效的多故障诊断方法。

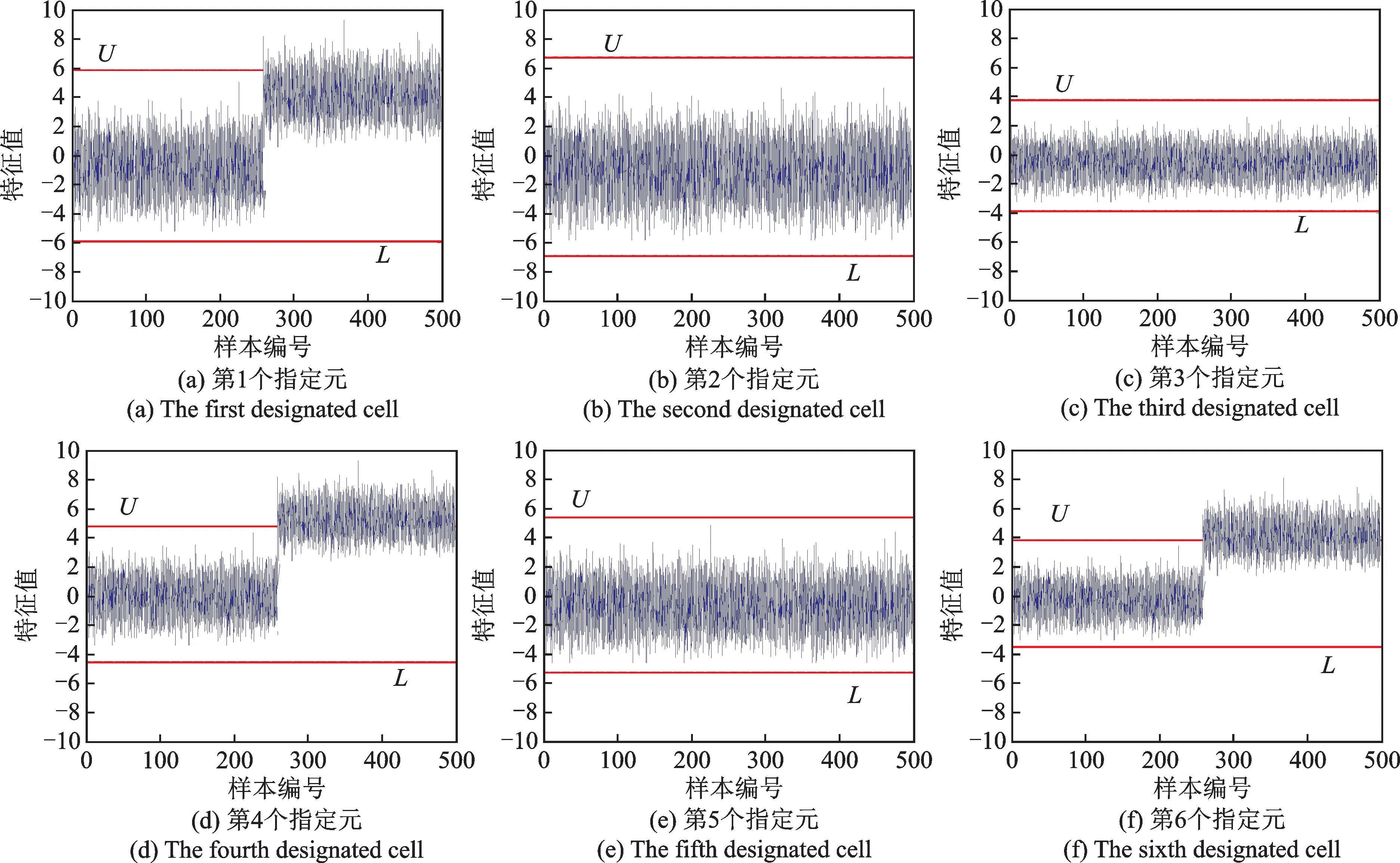
图2 各指定元的Shewhart图Fig.2 Shewhart diagram of each designated cell

3 支持向量机

3.1 SVM模型建立

考虑到SVM模型的诊断效果需要与前面的NFODCA模型对比，仍采用前面的2/3单发故障数据和2/3正常工况数据作为训练集，并发故障数据和剩下的1/3单发故障、1/3正常工况数据作为测试集。通过对训练集进行训练，优化SVM参数，建立模型，并用测试集数据验证SVM模型的可靠性。

SVM的主要参数包含惩罚参数c以及核函数参数g，通常对于这两个参数的选择是经过大量的实验分析得出的［7］，耗时耗力。为了快速得到最佳的参数c和g，使SVM的分类效果更好，采用网格寻优和K-折交叉验证方法。网格寻优即先在一定范围上粗略选择找出c和g，然后在c，g周围进行参数的精细选择［8］。K-折交叉验证方法的主要参数为折叠次数K，文中取K=5，即5折交叉验证方法。首先把制冷设备的数据样本分类成5组子集，将前4组样本作为训练集，最后1组样本用于测试，然后循环4次，每次都得出一个均方误差（mean square error，简称MSE）。将数据进行5次训练，且每次训练后将得到的数据进行整理分析，然后将5次的MSE取平均值。最后以MSE最小原则选取c值和g值作为SVM建模的最优参数［9］。

根据前面得出的最优参数，按照分而治之的原则，总故障样本集Y首先按d1故障分为正样本（含有d1故障样本）Fd1和负样本（不含d1的故障样本）FNd1，然后对这个二值分类问题建立SVM-d1分类器［10］；同理，再将Y分别按故障d2，d3，d4，d5，d6建立二值分类器。如果Y由多个分类器诊断为包含故障，则根据表决原则，判定故障样本Y包含多个故障［11］。

假设样本数据Y为含有d2，d3故障的数据，首先用SVM-d1分类器对其进行诊断，Y通过诊断表现为不含d1故障，则其决策函数R1可以定义为0；然后将Y用SVM-d2分类器诊断，Y通过诊断表现含有d2故障，则其决策函数R2可以定义为1；同理得到决策函数R3，R4，R5，R6的值。这样诊断下来综合的评定决策函数R表现为0/1/1/0/0/0，由此可以得到此时的故障Y同时含有d2，d3故障，同理可以得到其他各类故障所对应的决策函数。

3.2 SVM模型验证

首先找出SVM的主要参数即惩罚参数c和核函数参数g，SVM模型在数据处理过程中自动选择了参数c=10，g=0.1，这是随机得到的结果，具有主观性。因此通过网格寻优的方法优化参数，图3为参数c和g的粗略优化和精细优化过程，横坐标表示log2c的范围，纵坐标表示log2g的范围，均无量纲。

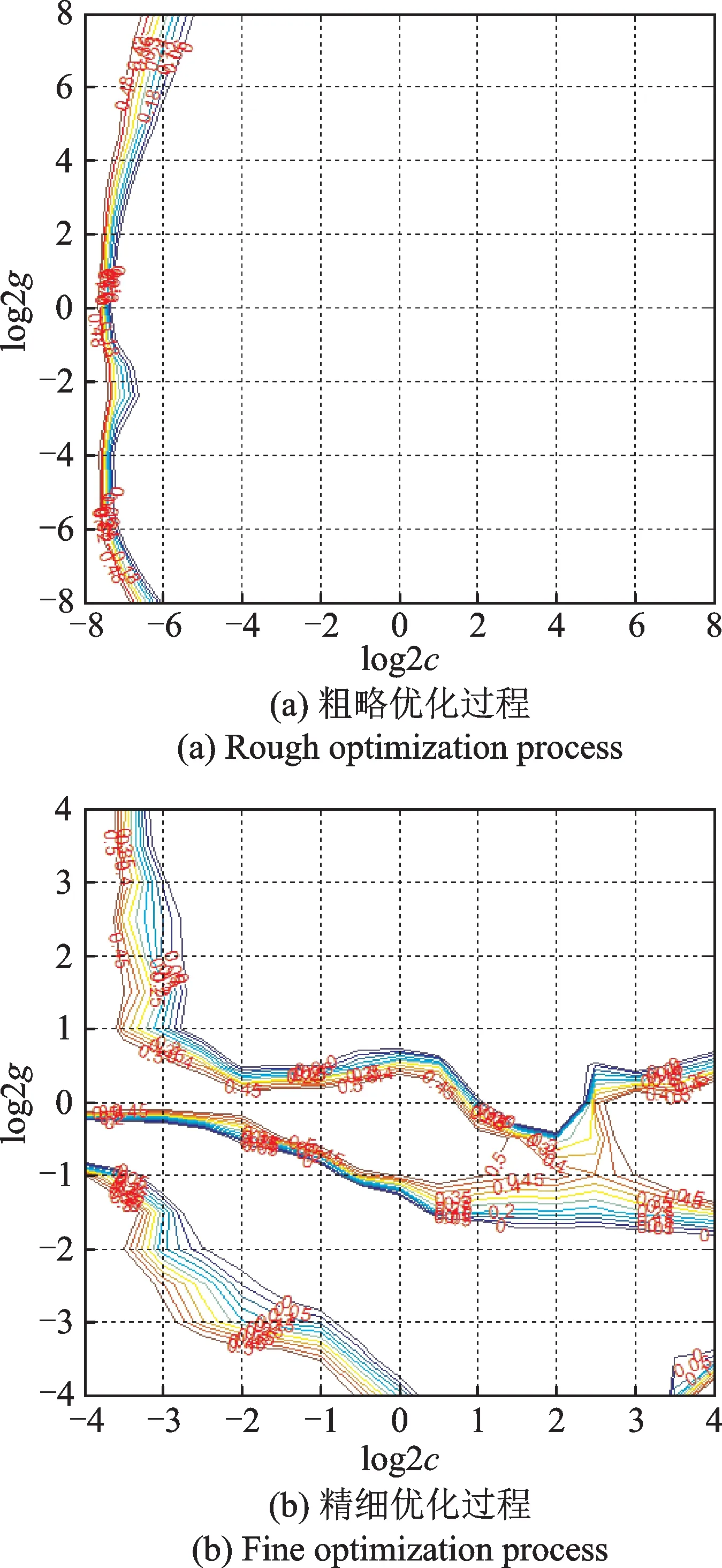
图3 参数粗略和精细优化过程Fig.3 Rough and fine optimization of parameters

图3 （a）为参数c和g的粗略优化过程：在2-8～28中 粗 略 得 出c=8.031 4，g=4.358 97，MSE=0.109 92，粗略确定了c和g的数据范围；图3（b）为精细优化过程：缩小范围在2-4～24中查找c和g，最后 得到最 优的c和g为cb=6.062 9，gb=2.297 4，并将其作为SVM此次运算的参数。使用5折交叉验证方法对并发故障进行诊断，并将故障诊断加过与故障模拟实验采集数据的故障记录对比得出故障命中率和虚警率。表3对比了5折交叉验证下经网格优化后使用的参数优化前后对并发故障的诊断结果。

由表3可知，选择默认设置（c=10，g=0.1）时，制冷设备故障诊断的平均正确率为46.75%，MSE平均值为0.634；而使用优化得到的参数（c=6.062 9，g=2.297 4）后，制冷设备故障诊断的正确率有了明显提高，而且每个折次下都有较高的正确率，平均正确率达到了96.80%，MSE平均值为0.027，证明该SVM模型对制冷设备故障诊断具有较高的准确率。

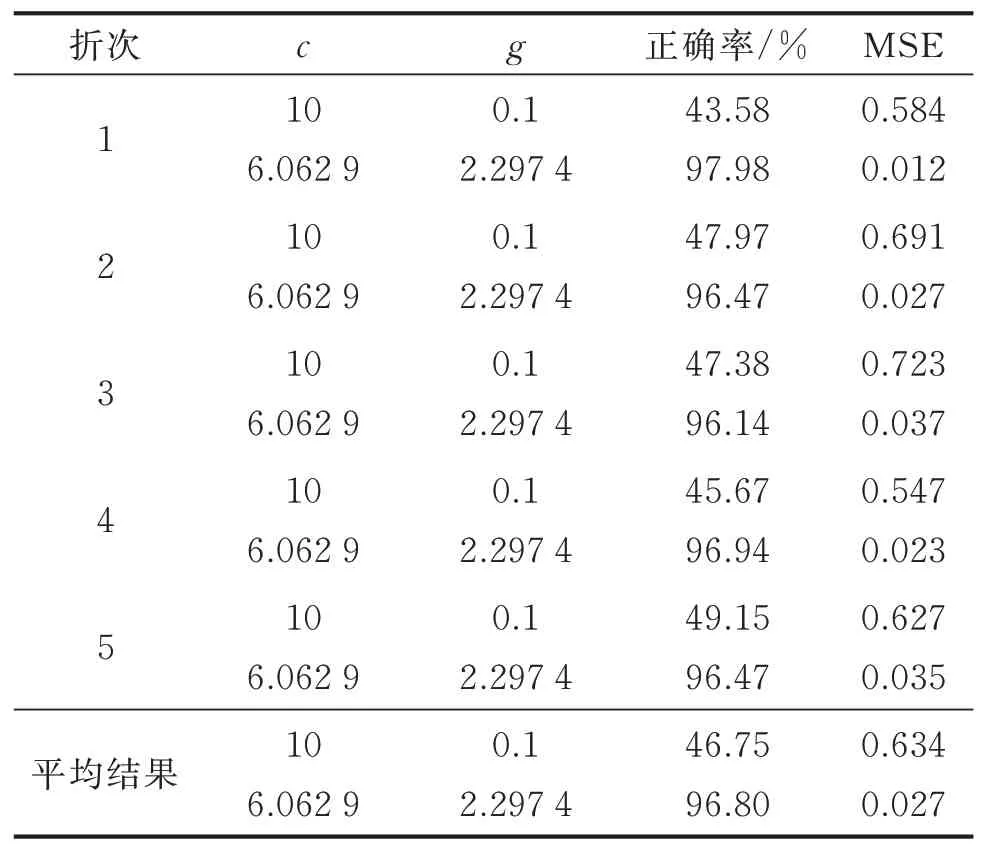
表3 5折交叉验证下参数优化前后故障诊断结果Tab.3 Fault diagnosis results before and after pa‑rameter optimization under 5-fold cross vali‑dation

4 信息融合

4.1 SVM模 型 与NFODCA模 型 对 比

将测试集数据分别用支持向量机（SVM）模型和非完全正交指定元分析（NFODCA）模型诊断，各类故障命中率和虚警率对比如表4所示。

由表4可见，非完全正交指定元分析（NFODCA）和支持向量机（SVM）两种模型对制冷设备的故障均有较高的准确率，且两种方法对不同故障识别度不同，各自在不同类型故障的识别有一定优势。

4.2 加权证据理论信息融合

对于制冷装置的并发故障诊断，如果只采用单一的诊断结论，极易造成误诊。前面分别从非完全正交指定元分析（NFODCA）和支持向量机（SVM）两种模型研究了制冷设备的并发故障，如果采用多专家集成诊断的方式，将不同方法的诊断结论进行融合决策，那么将会大大提高制冷设备故障诊断结论的准确性和全面性［12］。

文献［13］证明基于加权证据理论融合具有较好的聚焦能力，因此采用该方法对非完全正交指定元分析（NFODCA）和支持向量机（SVM）两种模型的诊断结果进行信息融合。将训练集中的每组数据视为一个证据组，将16种不同类型的制冷设备故障定义为一个空间Θ{F1，F2，…，F16}作为辨识框架，Θ是由相互排斥的命题组成的有限完备集。2Θ为Θ的幂集，表示Θ所有子集的集合。在2Θ上定义基本概率分配函数m：2Θ⊆[0，1]，m满足下列条件

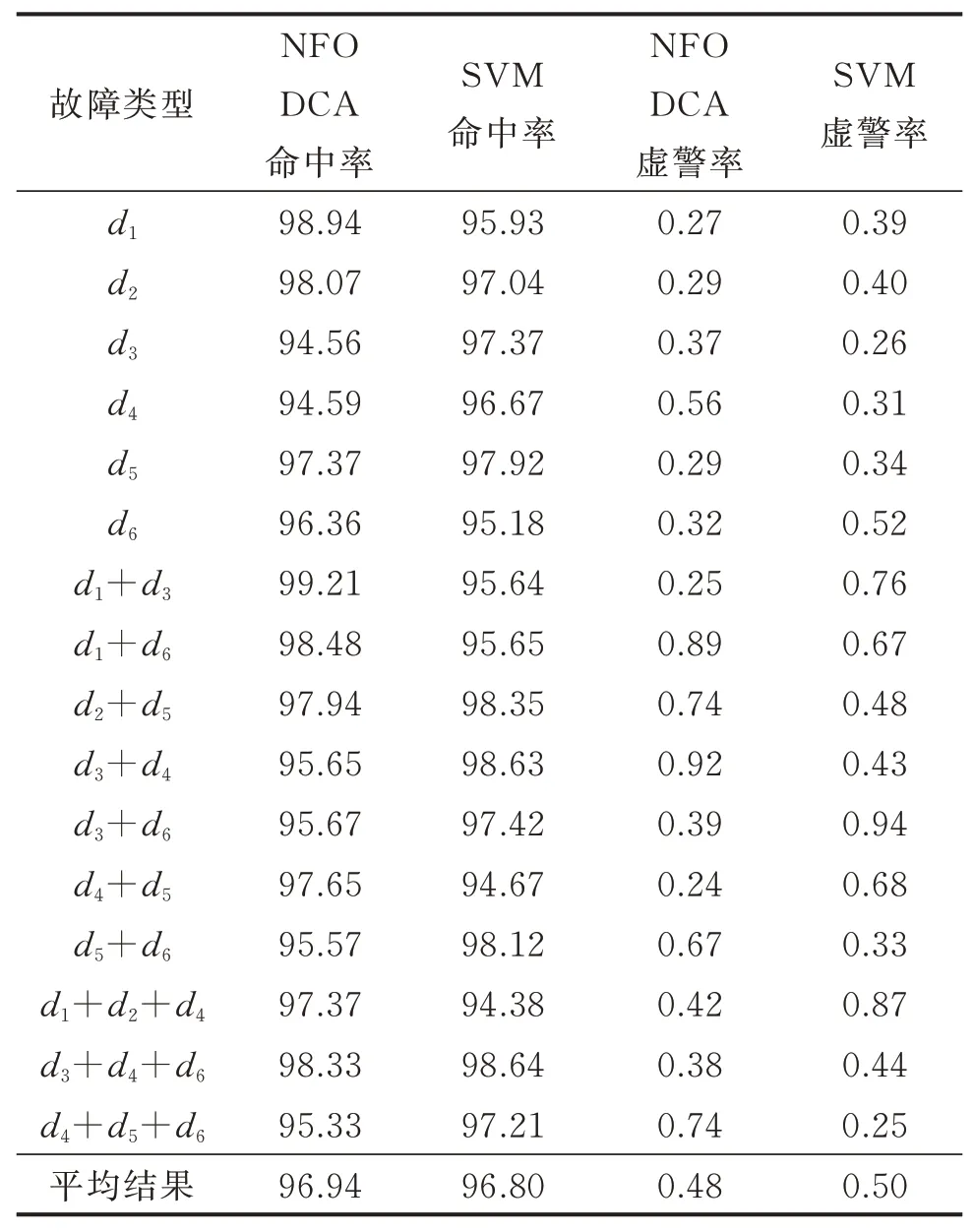
表4 SVM和NFODCA模型对各类故障命中率和虚警率对比Tab.4 Comparison of SVM and NFODCA models for various failure hit ratios and false alarm rates %

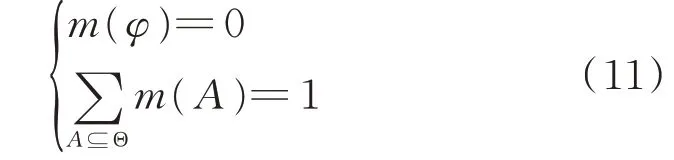
笔者采用了两种故障诊断方法，诊断结果中有两种待组合证据体E1，E2，对应基本概率分配函数分别为m1，m2，对应焦元分别为Ai，Bj，Ai，Bj的公共焦元为Cl，m1，m2之间的冲突程度系数为K。根据不同证据源的可靠程度分配权重系数，对相应故障敏感度较高的证据源赋以较高的权值，另一个模型赋以较低的权值，具体权值由多次实验后对比平均命中率和虚警率择优选出［14］。设E1，E2的权重系数分别为w1，w2，满足w1+w2=1，定义N个证据源对焦元的平均支持程度为

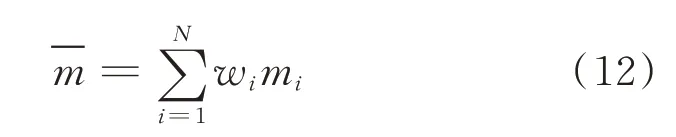
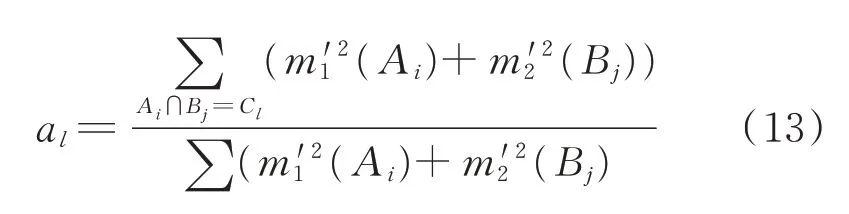
因此，加权证据理论融合公式为

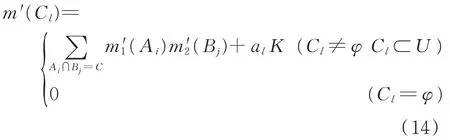
将NFODCA与SVM模型的证据体经上述方法融合后得到的故障诊断结果与故障模拟实验采集数据的故障记录对比，得出故障诊断命中率和虚警率如表5所示。由表5可以看出，制冷设备的故障识别结果经加权证据理论信息融合后更为精确，平均命中率达到了99.10%，平均虚警率降低至0.21%。

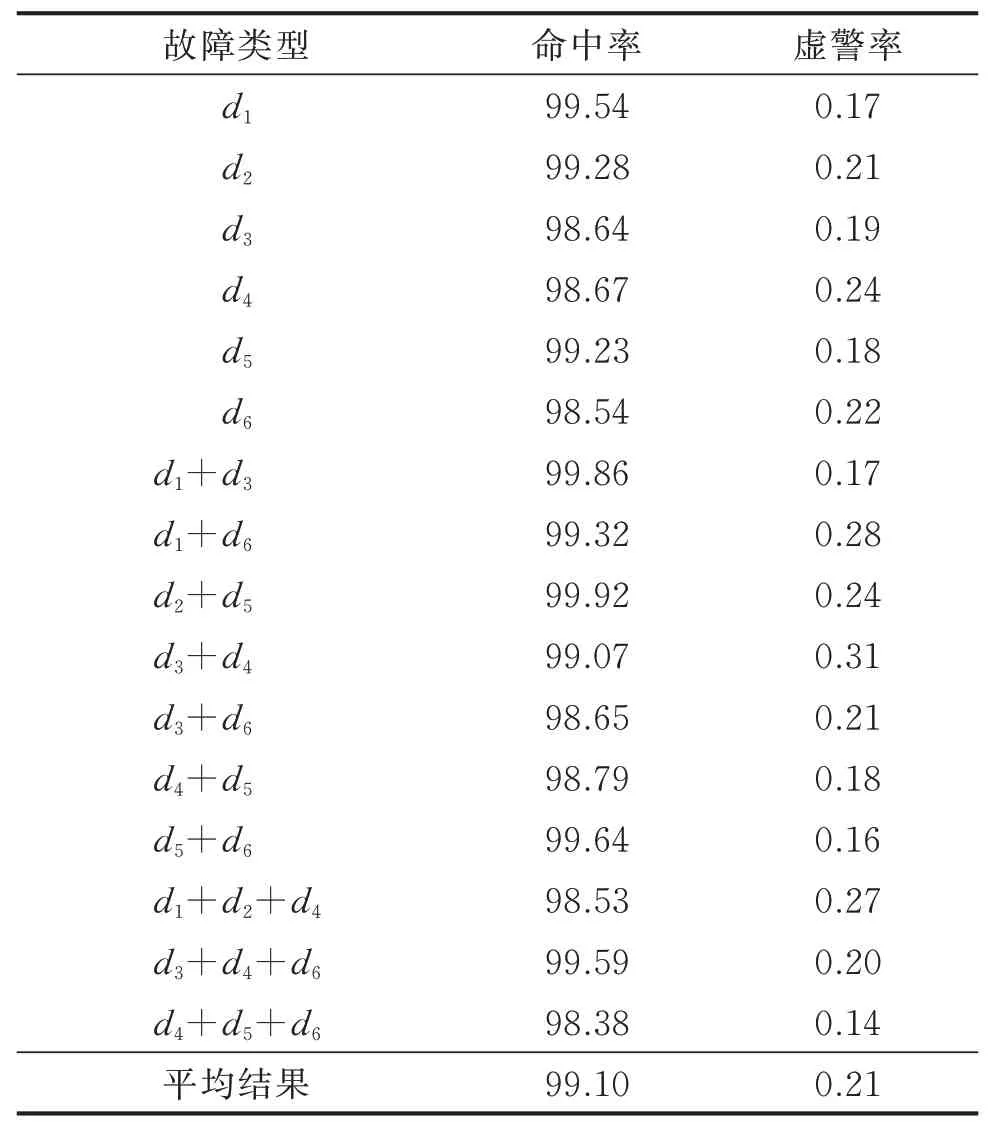
表5 信息融合后各类故障命中率和虚警率Tab.5 Hit rate and false alarm rate of various faults after information fusion %

5 结论

1）非完全指定元分析（NFODCA）和支持向量机（SVM）两种数据挖掘方法在训练集无并发故障数据，仅在测试集中包含并发故障数据的条件下对制冷设备的故障诊断均有较高的准确率，表明这两种方法均具有对未知并发故障类型进行判断的能力。其中非完全正交指定元分析（NFODCA）的平均命中率达到了96.94%，平均虚警率为0.48%；支持向量机（SVM）的平均命中率达到了96.80%，平均虚警率为0.50%。这两种方法对不同故障识别度不同，各自在不同类型故障的识别有一定优势。

2）非完全正交指定元分析（NFODCA）和支持向量机（SVM）两种方法的故障识别结果经加权证据理论信息融合后，平均命中率提高了2.23%，平均虚警率降低了0.28%。说明这两种数据挖掘方法和信息融合技术结合应用后可以对制冷设备的并发故障得到更为准确的判断。