基于协整理论的滚动轴承退化特征提取∗

李耀龙，李洪儒，王 冰，于 贺

（1.陆军工程大学导弹工程系 石家庄，050003）（2.西北核技术研究所 西安，710024）

（3.上海海事大学物流工程学院 上海，201306）

引言

滚动轴承是旋转机械中的重要零部件之一，起到支撑机械旋转体、降低摩擦力的作用，同时也是旋转机械中最为广泛且最易失效的零部件之一。在当前针对滚动轴承的分析研究中，一方面集中在故障诊断领域［1］，另一方面致力于轴承的故障预测研究。通过开展滚动轴承的全寿命试验，提取退化特征，分析其性能退化的规律，最后实现故障预测［2］。

有效的退化特征是实现预测的前提，许多综述对滚动轴承的退化特征进行了分类和总结。Lei等［3］将退化特征分成两类：①具有物理意义的特征，该类特征一般运用统计学和信号处理方法提取，包括常用的统计学特征、时域频域特征等；②虚拟特征，该类特征主要是通过融合算法得到。文献［4-5］将退化特征分为时域特征、频域特征和时频域特征等3类。然而，传统的退化特征缺乏一致性趋势，即不同的全寿命数据由于自身退化过程不同，其特征往往具有个性，不同全寿命数据的相同特征之间往往不具有一致的退化趋势。寻找不同全寿命数据间的相似或一致的变化规律，对建立退化模型具有重要意义［6］，同时也对深入挖掘滚动轴承退化过程的机理具有重要参考价值。

在以往的特征分类中包含了两小类传统的退化特征：①具有上升趋势的能量特征，以RMS为典型，RMS以其良好的性能被广泛应用于轴承的退化状态识别和剩余寿命预测中［7］；②具有下降趋势的复杂度特征，例如近似熵、样本熵及排列熵等。在研究过程中，可以发现能量特征和复杂度特征存在反向同步性，因此，推断二者可能存在协整关系。

基于以上分析，笔者在对能量特征和复杂度特征的分析基础上，拟将协整理论引入到滚动轴承的预测特征提取中。对能量特征和复杂度特征中的特征代表进行协整分析，并提取基于协整理论的滚动轴承退化特征。在此基础上，采用多组全寿命试验数据集，对所提特征的性能进行验证。

1 协整理论

通常，可以采用单位根检验来判断时间序列的平稳性，当存在单位根时，时间序列是非平稳的。ADF（augmented dickey-fuller）检验是常用的单位根检验法［8］。时间序列若经过d-1阶差分仍不平稳，经过d阶差分才平稳，称该序列是d阶单整的，记作I（d）。

Engle等［9］给出了协整的定义：由n组的d阶单整序列组成的向量yt=[y1t，y2t，…，ynt]T，如果存在一 个 向 量β=[β1，β2，…，βn]使 得 线性 组 合βyt=β1y1t+β2y2t+…+βn ynt是d-b阶单整，其中b＞0，那么认为yt=[y1t，y2t，…，ynt]T是（d，b）阶协整，记为yt～CI（d，b），向量β称为协整向量。常见的协整关系为CI（1，1）。协整意味着单整序列之间存在长期稳定的均衡关系，或者说存在特定的内在均衡机制在维持着单整序列间的长期稳定关系。协整检验的常用方法有E-G（engle-granger）检验法和Johansen检验法［8］。E-G检验法较为简单，适用于二组向量的协整检验。笔者采用E-G检验法。在进行E-G检验法之前，首先要确定待检验时间序列的单整阶数，可以通过ADF检验来确定。

2 能量特征与复杂度特征

2.1 能量特征

能量特征反映的是轴承在运行过程中的能量变化，式（1）列举了常见的能量特征。E1～E7分别为方根幅值、均方根值、绝对均值、峰峰值、最大值、最小值和频谱平均值。为了方便，在最小值前加了一个负号，使其为正。

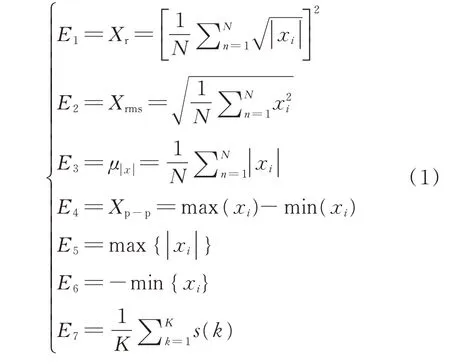
这里给出上述特征是能量特征的原因。简单来说，可以把每一个振动点的振动简化成简谐运动，其位移符合x=Acos（wt+φ），假定振动点的质量为m，那么其动能为

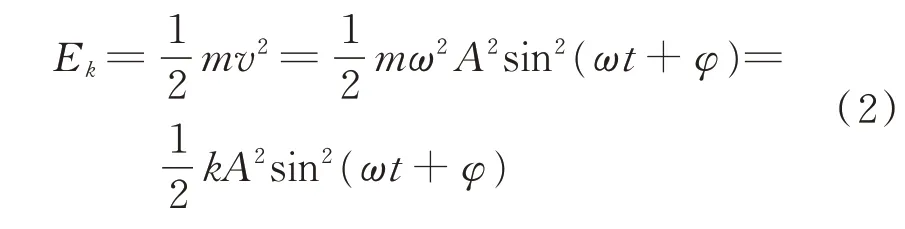
其势能为

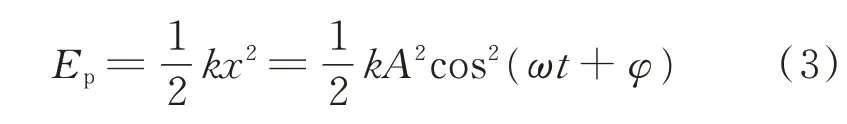
振动点的总能量为

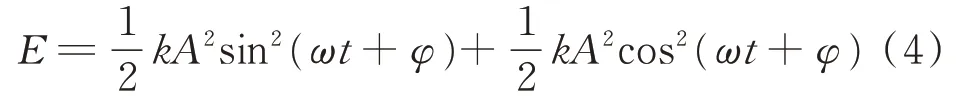
振动点的能量与振幅的平方成正比。不同的振幅反映的是不同的能量。上述7个特征都代表着某种具有物理意义的振幅。以常用的美国IMS中心的全寿命试验数据集中失效模式为外圈故障的Bearing2-1为例，将其能量特征绘制如图1所示。从图1可以看出，几种能量特征的走势相似。通过ADF检验可以得到E1，E2，E3和E7为I（2）；E4，E5，E6为I（1）。根据定义，同阶单整才可以进行E-G协整检验，在显著性水平为0.1的条件下，E1，E2，E3之间具有协整关系；E4，E5，E6之间具有协整关系。也就是说，E1～E3具有相同的变化趋势，E4～E6具有相同的变化趋势。E7虽代表着某种能量特征，但与RMS之间在当前显著水平下不具有协整关系，原因在于E7在求取的过程中存在傅里叶变换，而傅里叶变换本身存在混叠、泄漏等问题。E4～E6表征了每组信号的极值，稳定性较差；而E1～E3表征了每组信号的平均能量，稳定性较强。因此，可以选择E1～E3中的任意一个特征代表能量特征。因RMS在工业上应用广泛，故选择其作为能量特征的代表。

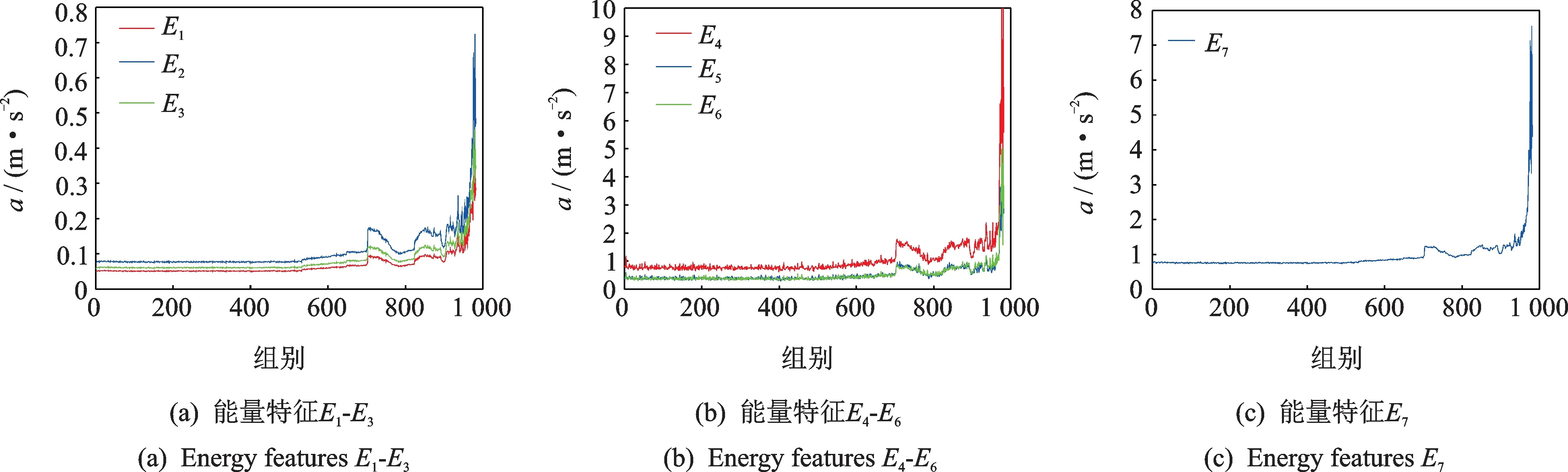
图1 IMS中心数据集Bearing2-1的能量特征Fig.1 The energy features of Bearing2-1 of IMS center

2.2 复杂度特征

复杂度特征能反映信号的复杂程度。常用的复杂度特征有近似熵、样本熵、模糊熵、香农熵、排列熵及L-Z复杂度等。其计算方法及参数设置详见文献［10-15］。为了测试各个复杂度的性能，在其计算过程中，相同的参数将设为一致，以减少参数对结果的影响。表1列出了复杂度的参数选取，其中相似容限均取0.2倍信号标准差。香农熵在计算时要对数据进行划分，设置极值间划分为50个区间。排列熵在计算过程中与香农熵相近，其嵌入维数与样本熵和近似熵不同，排列熵的嵌入维数越大，越准确，但耗时更长，经考虑将排列熵的嵌入维数设置为6。

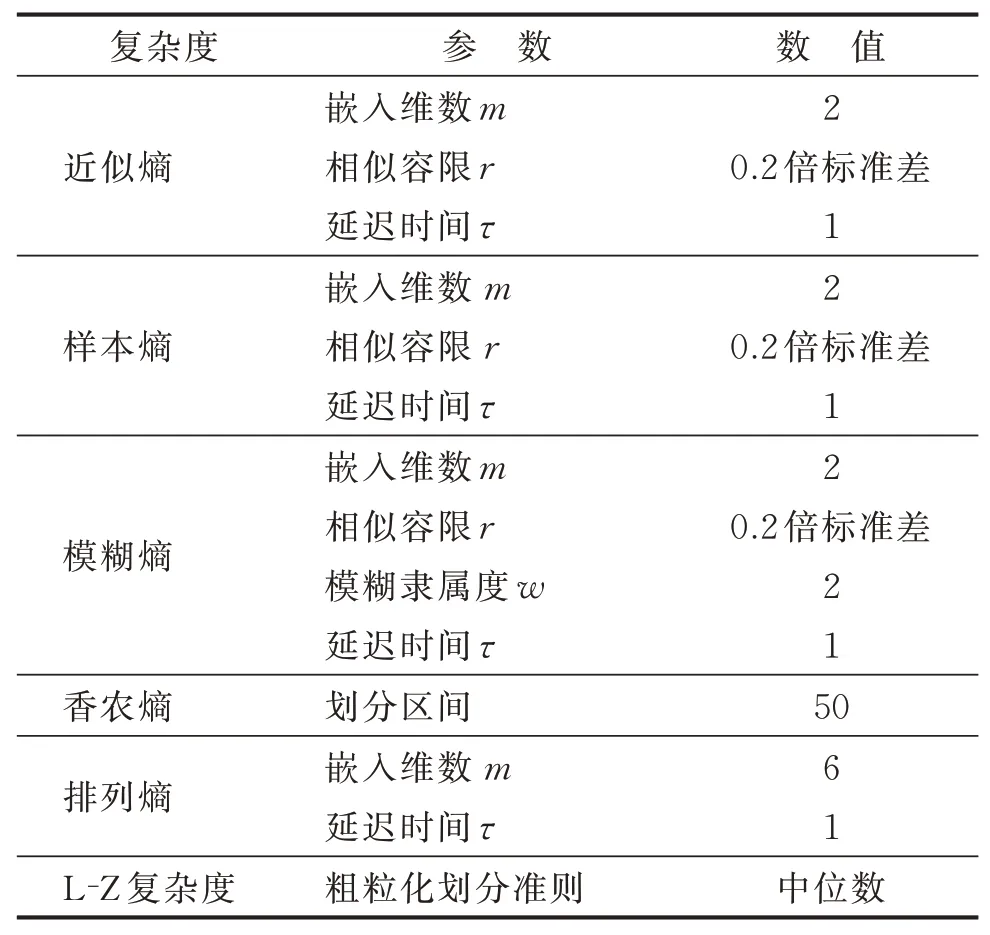
表1 复杂度的参数选取Tab.1 The selection of complexities'parameters

为了测试复杂度的性能，设置一个仿真信号，为S(t)=X(t)+e(t)，其中：X(t)为 正 弦 信 号，有X(t)=sin(2π×10t)；e（t）为附加高斯白噪声。采样频率为10 000 Hz，采样时间1 s。通过改变噪声的强度进而改变信噪比，观察仿真信号复杂度的变化如图2所示。理论上，复杂度随着噪声的增加应该增强。可以看出，香农熵与排列熵并不完全单调，说明二者的性能不太好。

为了进一步测试性能，需采用更一般的信号对复杂度进行测试。Logistic模型是典型的非线性系统，该模型中包含大量的周期和混沌信号，周期信号的复杂度应为0，混沌信号的复杂度应较高。图3给出了2.5＜μ＜4时的Logistic模型结果以及对应的最 大Lyapunov指 数（the largest Lyapunov exponent，简称LLE）。LLE可以反映所出信号的复杂程度，LLE＜0时表明信号是周期信号；LLE=0时为分岔点；LLE＞0时表明信号为混沌信号。将6种复杂度带入Logistic模型中，其结果如图4所示。

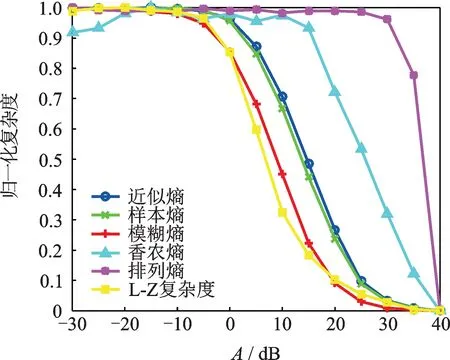
图2 仿真信号的复杂度随SNR变化的曲线Fig.2 The curve of six complexities versus SNRs

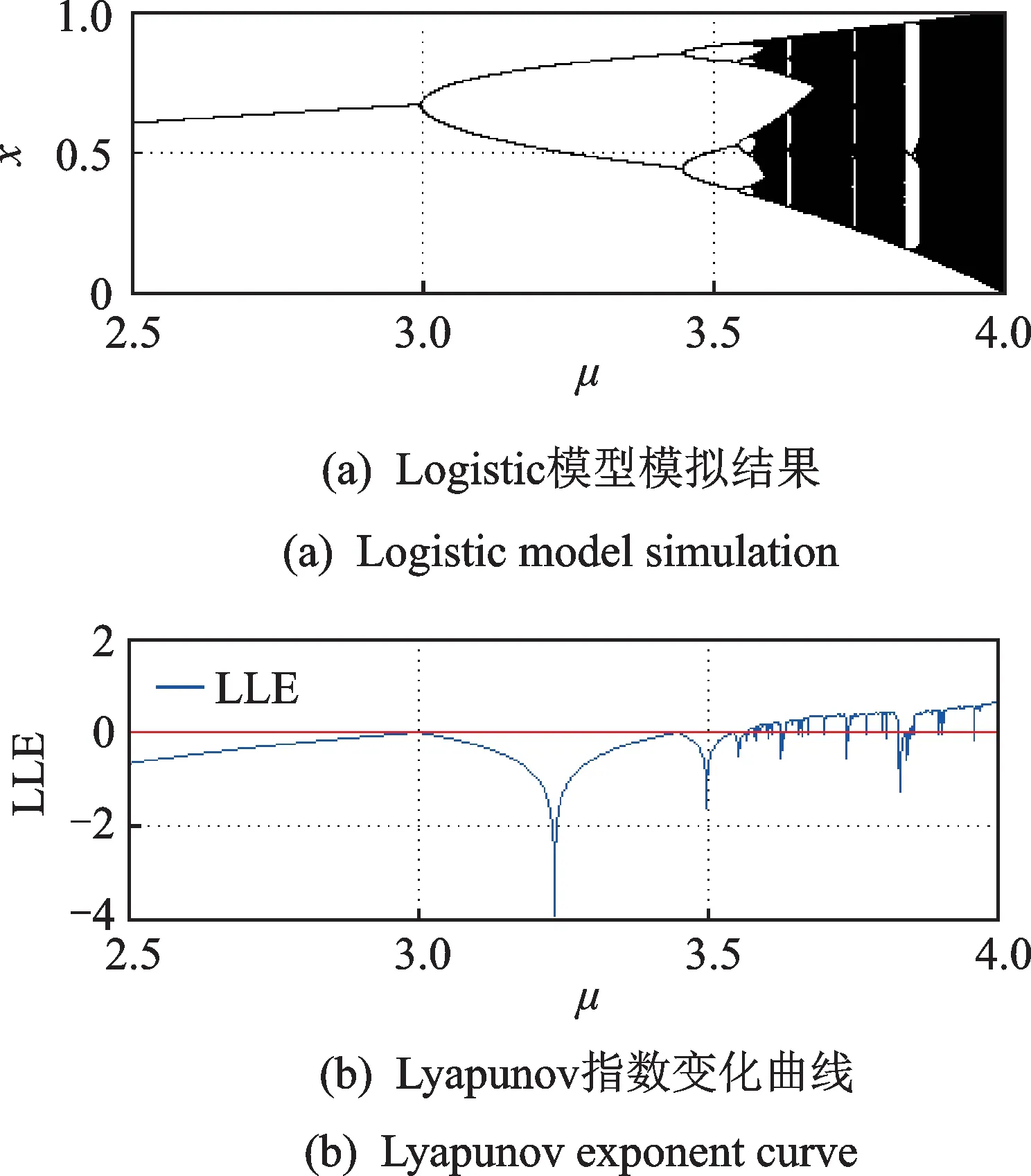
图3 Logistic模型及其LLEFig.3 The Logistic map and its LLE

图4 6种复杂度应用于Logistic模型的曲线Fig.4 The six complexities of the Logistic map

可以看出，香农熵和排列熵对周期信号的衡量存在误差。模糊熵在衡量μ=3.5时出现了偏差，这是由于模糊熵存在模糊隶属度而导致的问题。L-Z复杂度在μ=3.6左右发生了偏差，这是由于L-Z复杂度在计算过程中的粗粒化过程导致的。

综上，近似熵和样本熵在6个复杂度中表现较好。同时，作为近似熵的改进算法，样本熵在计算时不包含自身数据段的比较，其优越性体现在较少地依赖时间序列长度，结果的一致性较好。所以，样本熵在这6个复杂度中的性能最好。这样，就可以把样本熵作为复杂度的代表。

3 基于协整理论的退化特征提取

上文已经确定了能量和复杂度特征的代表分别是RMS和样本熵，同时也说明了能量特征反映了信号的幅值，其平方才反映信号的某种能量。故以RMS2和样本熵为基础，利用二者进行协整融合，其基于协整理论的退化特征提取流程如图5所示。

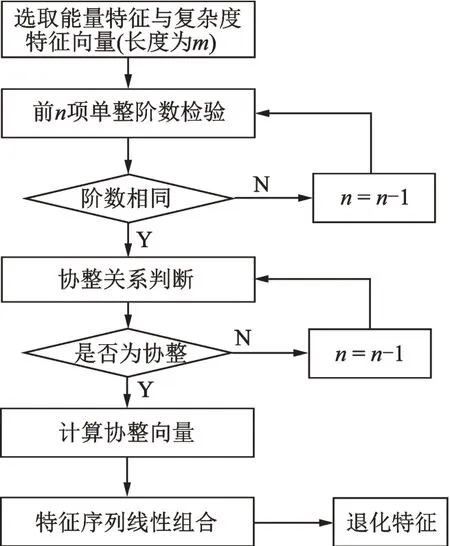
图5 基于协整理论的退化特征的提取流程Fig.5 The extraction procedure of the degradation feature based on cointegration theory

要进行基于协整理论的退化特征提取必须确定二者间是否存在协整关系。首先，二者的单整阶数须一致。以Bearing2-1为例，先要确定RMS2和样本熵的单整阶数，经ADF检验，样本熵为I（1）序列，RMS2为I（2）序列。进一步检验发现，n＜966，RMS2为I（1）序列。此时RMS2和样本熵不具有协整关系。依次减小n，并对RMS2和样本熵进行E-G检验，发现n=914时，二者出现协整关系。定义该点为转变点。在确定协整向量后，按照协整向量绘制RMS2和样本熵的线性组合，如图6所示。

可以看出，基于协整理论的退化特征呈现明显的两段性。914组之前，序列平稳，波动性很小；914组至最后失效，序列呈单调上升趋势。

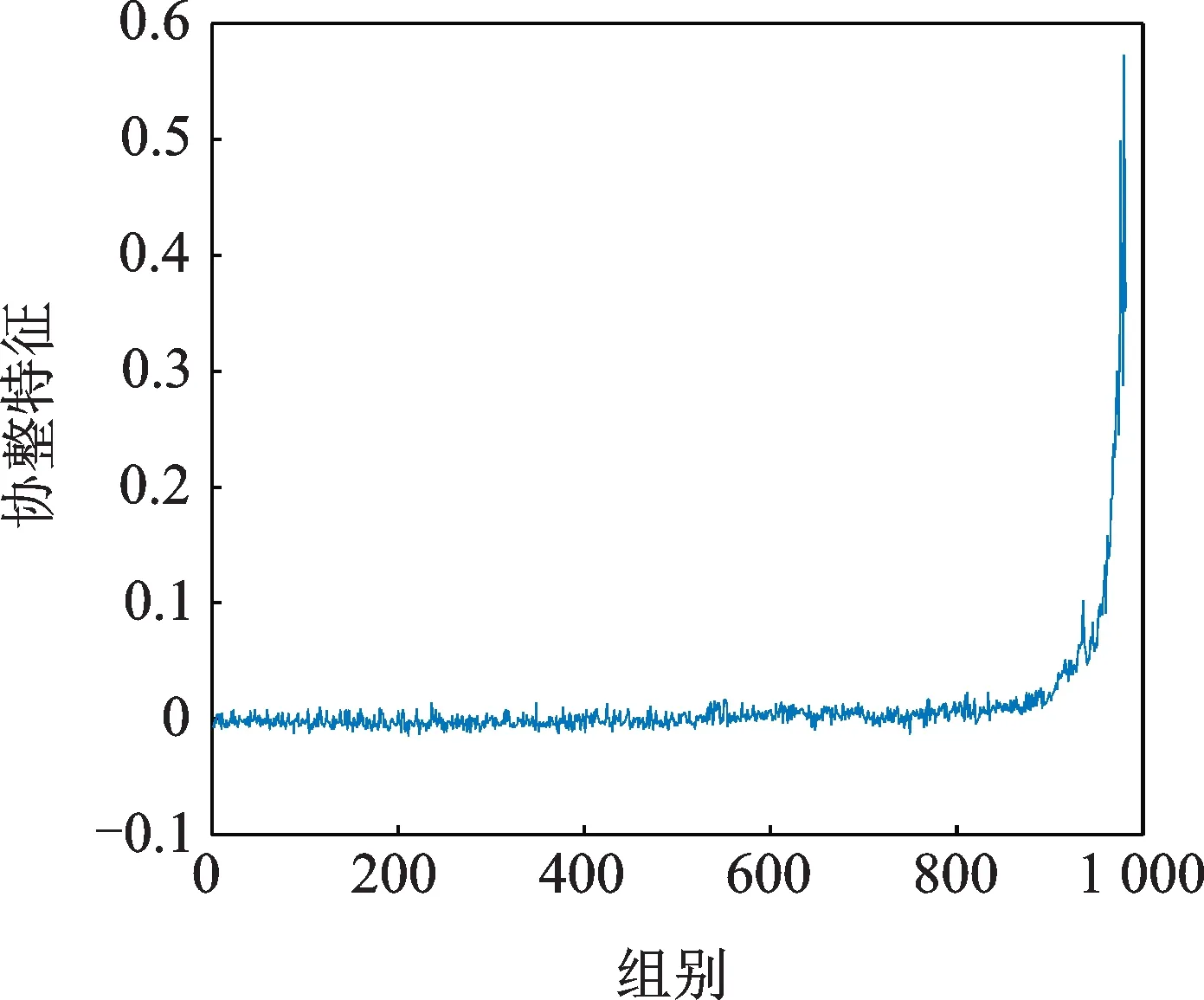
图6 基于协整理论的退化特征Fig.6 The degradation feature based on cointegration theory

4 实例验证

4.1 轴承全寿命数据集

为了验证所提特征的两段性和一致性，文中将选取多组轴承全寿命数据用于支撑。数据来自美国IMS中心的全寿命试验数据集，其试验详情可见文献［16］。笔者选取失效模式为外圈故障所提及的Bearing1-4作为测试集1，以失效模式为内圈故障的Bearing1-3作为测试集2。测试集1，2都包含2 155组数据。选取Bearing2-1为测试集3，包含982组数据。

4.2 基于协整理论的退化特征的有效性验证

首先，将测试集的RMS和样本熵进行提取，其曲线如图7所示。从图7可以看出，各个测试集的退化曲线表现各不相同。具体分析，测试集1表现出了“愈合”现象，RMS先上升后下降。关于滚动轴承中的“愈合”现象可参考文献［17-18］。测试集2的RMS表现出了长时间的平稳，最后快速上升，此时也能观察到“愈合”现象，可以发现在160组左右RMS出现了阶跃，分析原始信号，此处存在关机，说明开关机对工况是有影响的，在进行全寿命试验时应减少开关机频率。测试集3的RMS开始较平稳，而后上升，出现阶跃，而后出现了两次“愈合”现象，表现出了强烈的长期波动性，并不利于预测。对比图6可以看出，通过协整方法可以有效减小退化前、中期的RMS和样本熵的长期波动性。

可以看出不同的测试集其RMS和样本熵各有特点，没有一个统一的变化规律，缺乏一致性。通过E-G检验各测试集的RMS2与样本熵的协整性，可以验证测试集的所有RMS2与样本熵的部分序列间具有协整性。根据所提方法，将测试集1，2基于协整理论的退化特征进行提取，如图8所示。

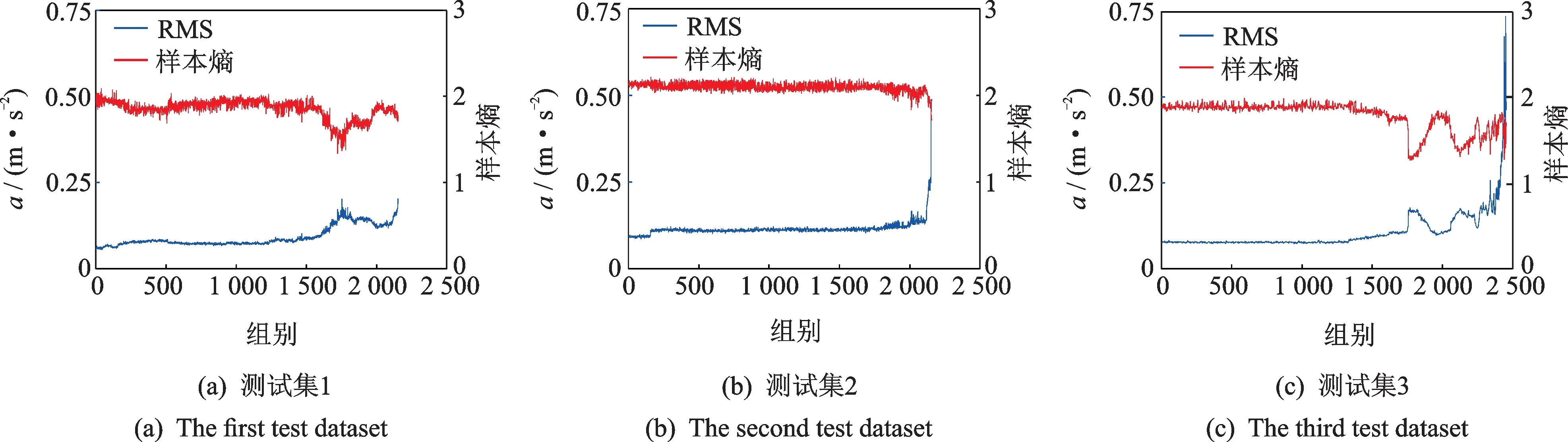
图7 测试集的RMS和样本熵曲线Fig.7 The RMS and sample entropy of the test datasets

从图6，8得知，3个测试集基于协整理论的退化特征具有明显的两段性。在全寿命的前、中期表现出平稳性。当滚动轴承处于失效期，该特征表现出非平稳性，并具有一定的单调性。几个测试集的RMS和样本熵表现出了不同的轴承退化过程，但经协整理论融合后，其融合特征表现出了一致性的演化规律，说明该方法可以统一不同轴承的演化过程，具有一般性。经协整理论融合还降低了RMS和样本熵在全寿命的前、中期的长期趋势性波动。

5 结果分析

现就为何所提取的退化特征具有一致性和两段性进行说明。以Bearing2-1为例，将其RMS2与所提特征放在一起进行对比，为了方便采用RMS代替RMS2，如图9所示。

根据Bearing2-1的RMS曲线可以推断该轴承的退化过程。从开始运行到第510组，RMS保持平稳，可知轴承处于正常状态；从510～700组，RMS持续上升，轴承处于轻微故障阶段；700组时，RMS突增，这可能是摩擦面上产生了凸起造成的，而后运行至823组，RMS经历了下降再上升的阶段，这主要是由于持续的摩擦作用使局部凸起的表面降低，而后RMS又经历了这种下降再上升的过程，此时轴承处于中度故障阶段；从900～982组，RMS持续上升，此时轴承处于重度故障阶段直至失效。

这种下降再上升的过“愈合”现象在轴承中具有普遍性，出现该现象的原因在于持续的摩擦作用使局部凸起的表面降低。而后由于故障加深，摩擦副表面又形成了新的凸起，如此往复。“愈合”现象说明轴承已经进入中度故障状态，它的出现虽有利于退化状态识别，但也会导致RMS的单调性下降，不利于轴承的预测。

反观所提出的基于协整理论的特征，其具有两段性。从开始运行到914组左右，其具有平稳性；从914组到最后失效，其快速上升。对其具有两段性进行分析。当轴承处于正常状态下，RMS平稳，样本熵也平稳。当轴承处于轻微故障阶段，摩擦面上出现凸起，导致能量上升，RMS上升；同时，凸起可导致信号的周期性增加，复杂度降低。当轴承处在“愈合”现象时，持续的摩擦使凸起变得平滑，这样导致能量降低，RMS下降；由于凸起变得平滑，周期性也就相应降低，致使复杂度升高。总之，在914组之前，RMS2与样本熵保持着同步性，这样使两序列的线性组合为平稳序列。

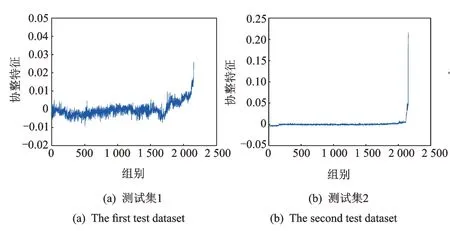
图8 测试集1,2的基于协整理论的退化特征提取Fig.8 The degradation feature based on cointegration of the dataset1 and 2

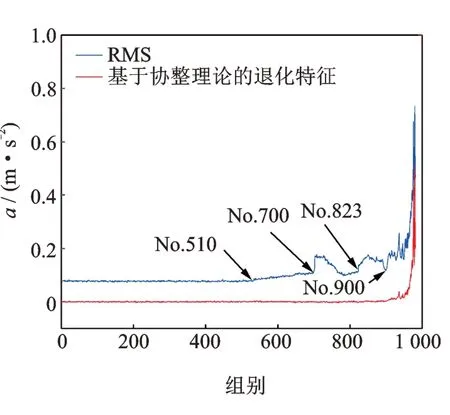
图9 RMS和基于协整理论的退化特征对比Fig.9 The comparation of RMS and theproposed feature

当轴承接近于失效，能量急剧增加，摩擦副表面上的凸起急剧增多，虽有平滑作用，但效果不明显。由于每个凸起都能形成周期性信号，那么整体的振动信号就是各个凸起引起的信号叠加，此时的信号周期性就不显著了，所以复杂度降低得不明显。这时，两序列的协整性消失，所提特征在此阶段明显上升。所以转变点可以看作局部故障向多点故障变化的转折点，当运行到转变点时，轴承距离失效已经不远，应当进行轴承的剩余寿命预测了。

文献［3］综述了特征是否适合于作为预测性能的指标，其中包括单调性、鲁棒性和趋势性。其表达式分别如下，其中count（）为满足要求的个数

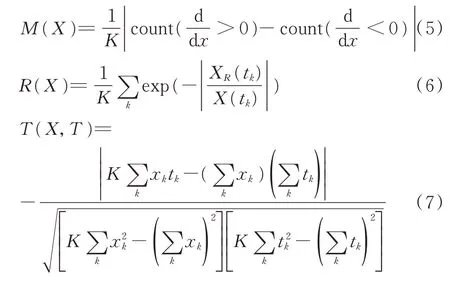
单调性是衡量特征单调的程度，在求取前应该进行平滑处理，降低噪声的影响。鲁棒性衡量的是特征的稳定程度，从而减少预测结果的不确定性，其中X（tk）=XT（tk）+XR（tk），即信号分为确定的趋势信号和平滑后的剩余信号。趋势性是指特征与运行时间的相关程度。3个指标的取值范围都是［0，1］，越接近于1说明特征相应的性能越好。求取3个测试集的预测性能指标，如表2所示。在求取时应当对特征进行归一化处理，在计算单调性和趋势性时忽略各特征平稳阶段带来的影响。平滑方法采用高斯滤波方法，窗口长度20。

从表2看，基于协整理论的退化特征具有明显的非减性特点。相对于RMS和样本熵，其在非平稳阶段的单调性更好。在鲁棒性和趋势性上，所提特征与RMS及样本熵处于同一水平。事实上基于协整理论的退化特征提取是一种融合特征的方法。融合算法包括线性和非线性降维方法，其中以主成分分析法（principal components analysis，简称PCA）和等距特征映射（isometric mapping，简称Isomap）为典型。以Bearing2-1为例，将RMS2与样本熵经PCA和Isomap融合后得到图10的结果。

表2 测试集特征的预测性能指标Tab.2 The prediction performance index of datas‑ets'features

从结果看，PCA与Isomap融合后特征与样本熵很相似。总体上RMS2与样本熵走势相反，经PCA与Isomap融合后的特征保持了其共有的趋势。区别于PCA和Isomap，协整融合是将二者中趋势不相同的地方提取出来，而将共有的趋势进行消除。

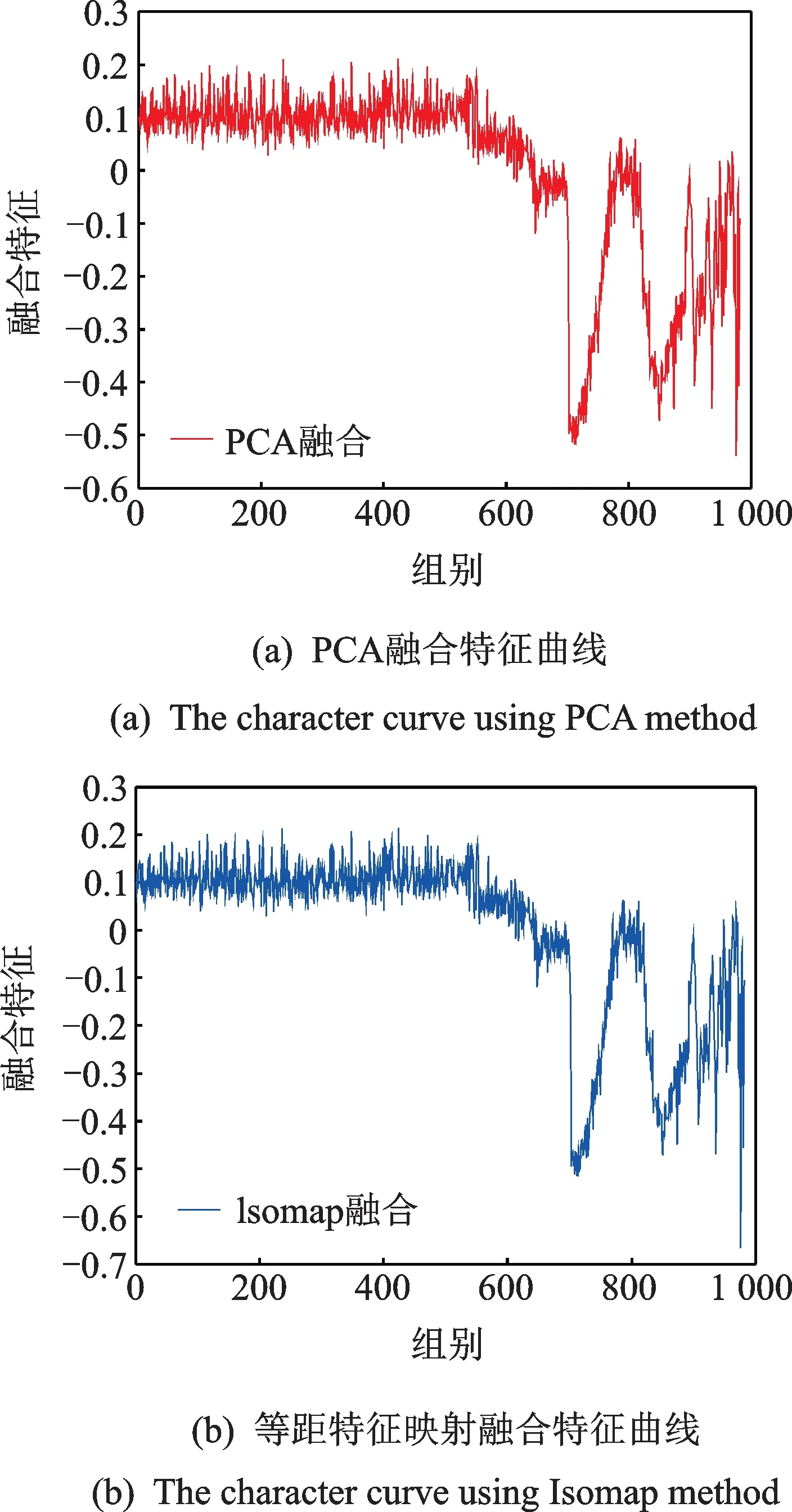
图10 Bearing2-1的RMS2与样本熵经PCA与Isomap融合后的结果Fig.10 The fusion result of Bearing2-1's RMS2 and sample entropy based on PCA and Isomap

6 结束语

笔者发现了滚动轴承全寿命数据中RMS和样本熵存在的协整关系，并提出了一种基于协整理论的滚动轴承退化特征的提取方法。所提取的退化特征有以下特点：具有良好的两段性，能够反映滚动轴承退化的前、中期和失效阶段的不同特性。同时，该特征可以降低RMS、样本熵在退化前、中期时的长期波动性。所提特征具有一般性，能够将不同的滚动轴承全寿命数据统一起来，得到具有一致性的演变过程。相比于RMS和样本熵，所提特征在非平稳阶段的单调性好，故障预测能力更好。