面内纵振复合模态直线超声电机模态识别方法∗

陈紫嫣，王 寅，曹 俊，时运来，黄卫清

（1.华侨大学机电及自动化学院 厦门，361021）（2.南京航空航天大学航空学院 南京，210016）（3.广州大学机械及电气工程学院 广州，510006）

引言

超声电机利用压电陶瓷的逆压电效应以及摩擦耦合将定子自身的微米级往复振动转化为动子宏观直线或旋转运动的执行机构［1-2］。自20世纪80年代至今，其发展日益迅速，它以自身重量轻、输出能量密度高、易于小型化和轻量化等优点，在精密驱动与控制领域应用广泛［3］。

根据超声电机定子振动的波动形式不同，可将超声电机分为行波、驻波和表面波超声电机。其中驻波超声电机以其结构多样化引起了研究人员的广泛关注［4］。为了实现驻波超声电机定子的驻波振动，压电陶瓷与金属基体的装配方式有贴片式和夹心式两种结构。其中贴片式结构紧凑，易于小型化［5-6］；夹心结构能够输入较高功率，在需要大推力的场合具有应用前景［7］。根据波动在定子内的振动方向的不同，驻波超声电机有面外振动式和面内振动式两种［8-9］。其中面内振动结构具有较小的厚度，能够在不增加驱动系统厚度的前提下实现作动。面内模态超声电机从结构特点可分为整体模态复合型和局部模态组合型两类［10-11］：整体模态复合是指利用板结构面内两个纵振或弯振模态进行组合设计定子，这类电机的典型代表有Nanomotion公司的L1B2模式的超声电机和PI公司的产品，这类电机在定子上不设槽结构，对加工精度具有较高要求，且异形模态的频率响应带宽要重叠这一要求难以达成；而局部模态组合型通常由单一低阶弯振或纵振模态的两个压电振子组合而成，通过两个振子振动的相位组合实现摩擦驱动，相对整体模态复合型更易实现响应带宽重叠，且不易受到边界条件的影响［12］。

在超声电机的设计及制造过程中，模态试验是检验电机设计是否合理、样机制作是否合格的重要途径。基于面内纵振模态贴片结构直线超声电机以其紧凑的结构及所选的面内工作模态在给电机带来小尺寸和便于装夹优点的同时，这些特征也使得定子的模态试验难以实施［13］。与同样是扁平结构的方板结构超声电机相比，方板结构定子的工作模态是面外模态［14］，其振型信息可通过测量垂直于结构所在平面的振幅及相位获取；而扁平的板状结构的面内模态则需要获取平行于振动平面的振幅及相位，这给该类结构的模态试验提出了挑战。

随着测量技术的不断进步，超声电机模态试验的方法也逐渐完善。在早期定子模态试验中，研究者借助动态分析仪测量定子导纳曲线［15］，不能获得振型结果。电子散斑激光测振仪可实现振型的测量，但不能定量测出振幅，并且易受外界干扰，使得其应用受限［16-17］。基于激光多普勒效应的多普勒激光测振系统可实现对定子表面振动的全面测量，可通过逐点测试的方式获得较大测量范围的振型。这类系统测试频段宽、精度高，可以快速地得到定子上各测量点的振型分布图。基于面内纵振模态的直线超声电机，其定子的振动模式为面内复合振动，激光扫描多普勒测振仪难以直接测量其面内振动模态，导致面内振动模态电机模态试验的困难［18］。

本研究将在介绍面内纵振复合振动模式直线超声电机的原理基础上，结合面外振动激光多普勒测量原理研究面内纵振复合模态超声电机模态识别方法，并通过样机试验对该方法的有效性进行验证。

1 电机定子模态试验原理

1.1 电机定子与振型

图1 所示为面内纵振复合模态超声电机电机的定子，定子为具有对称面的结构，由一对纵振压电振子、连接纵振压电振子端部的拱形结构以及连接纵振压电振子中部的支撑结构组成。每个压电振子金属基体的两个表面都粘贴有1片矩形压电陶瓷片。拱形结构的顶部设有锥形孔结合面，通过粘接装有氧化铝陶瓷球作为驱动足，用于提高定子的耐磨性。两个对称结构的纵振压电振子之间有一个支撑结构，用来提高定子刚度。压电振子长边外侧为V形结构。

定子上的压电陶瓷为贴片式粘接在金属基体上，陶瓷片的极化方向如图1中箭头所示，4片压电陶瓷片均沿厚度方向极化。位于同一侧的压电陶瓷片施加相同的电压激励信号，位于右侧的两片压电陶瓷片施加A相正弦信号，位于左侧的两片压电陶瓷片施加B相余弦信号，两信号频率振幅均相同。金属基体作为激励电压的参考零点。

为了叙述方便，上述A，B两相电压激励引起定子驱动足的振动响应分别用ua（t），ub（t）表示。定子在工作频率附近有两个工作模态，分别为面内同相振动模态和面内反相振动模态。将定子工作模态所在的平面设为xy平面，如图2所示。

定子在A相电压的激励下，其面内同相振动模态被激发，驱动足处产生沿y轴方向的往复振动，其振动响应可表示为

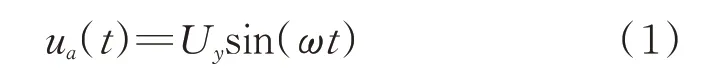
其中：Uy为y轴方向振幅；ω为角频率。

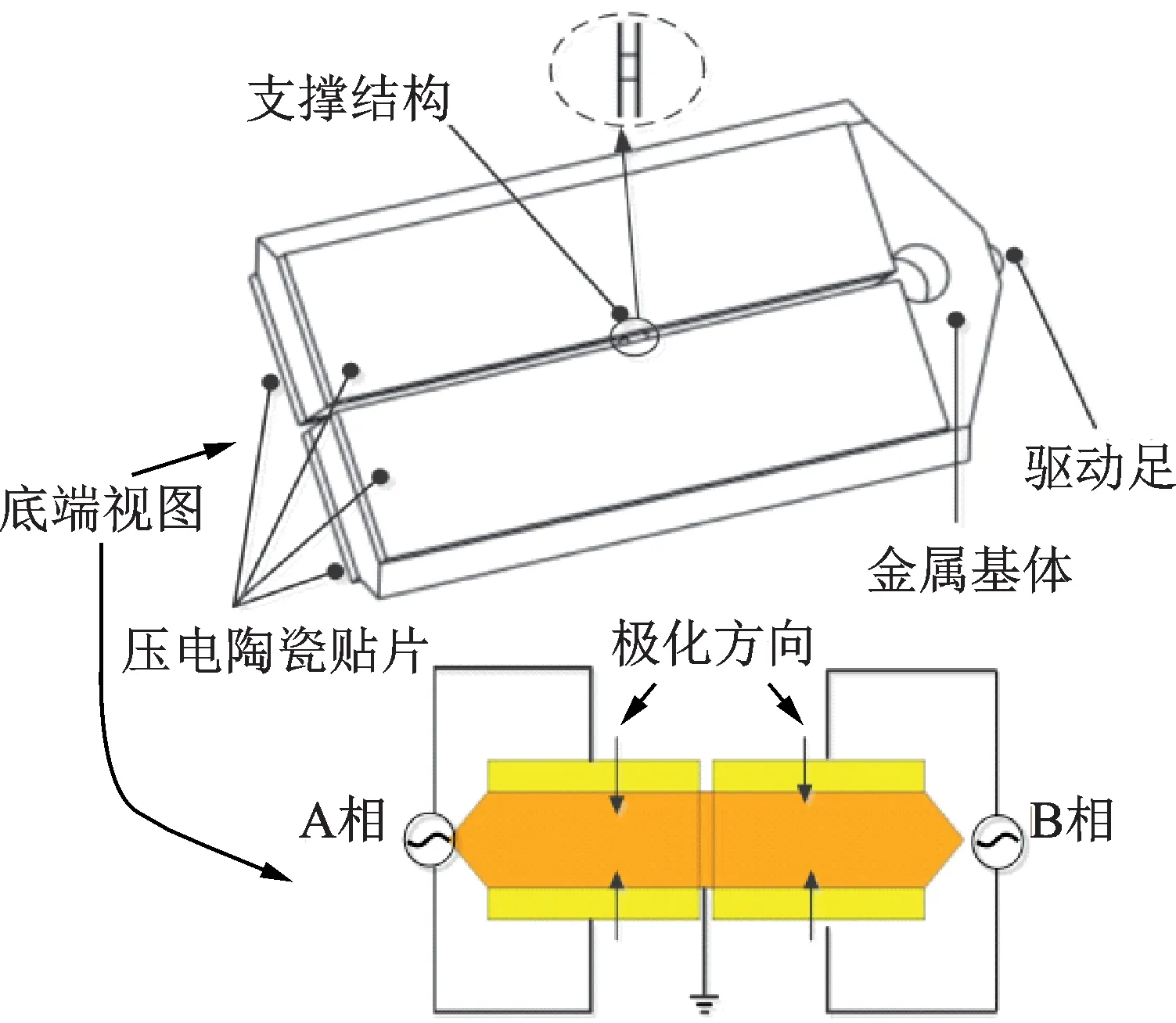
图1 定子结构Fig.1 Stator structure

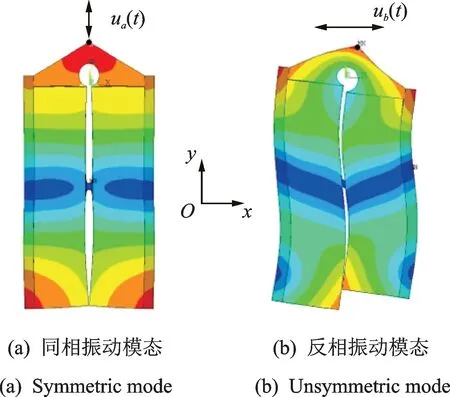
图2 定子的工作模态Fig.2 Two working modes of the stator

定子在B相电压的激励下，其面内反相振动模态被激发，驱动足处产生沿x轴方向的往复振动，其振动响应可表示为

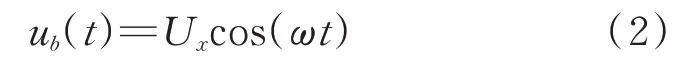
其中：Ux为沿x轴方向振幅；ω为角频率。

当A，B两相电压同时施加，联立上述两式可知，驱动足的振动轨迹为两个方向振动的叠加，其轨迹方程为椭圆方程

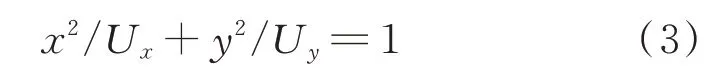
由上述分析可见，定子的工作模态的振型可视为两个纵振的压电振子振动的合成，纵振压电振子的振型为一阶纵振。两个振子在一阶纵振的节面和其中一端相连，两个纵振振型同相振动时驱动足沿y轴方向振动，反相则引起驱动足x轴方向的振动。

1.2 多普勒测量原理

多普勒激光测振系统是以光学多普勒效应为基础的一种非接触式测量系统，其高精度多点测量是由其中的激光干涉仪实现的，该测量系统中的高速摆镜用来实现对被测物体的扫描，测量得到的数据由计算机进行处理与评定，最终得出待测表面的振型。

多普勒测量系统如图3所示。试验时，由PC端产生数字信号，经过D/A转化为模拟信号后经过功率放大器放大成合适的激励驱动信号施加在定子的压电陶瓷元件上，定子在激励信号的作用下将产生振动［17］。定子在振动的同时其被测面接受并反射由扫描激光头内的干涉仪输出的稳频光束，获得的两信号差最后经过解码器进行数据处理输出模拟信号，再通过A/D转换进入PC端处理并显示其幅频曲线［18］。

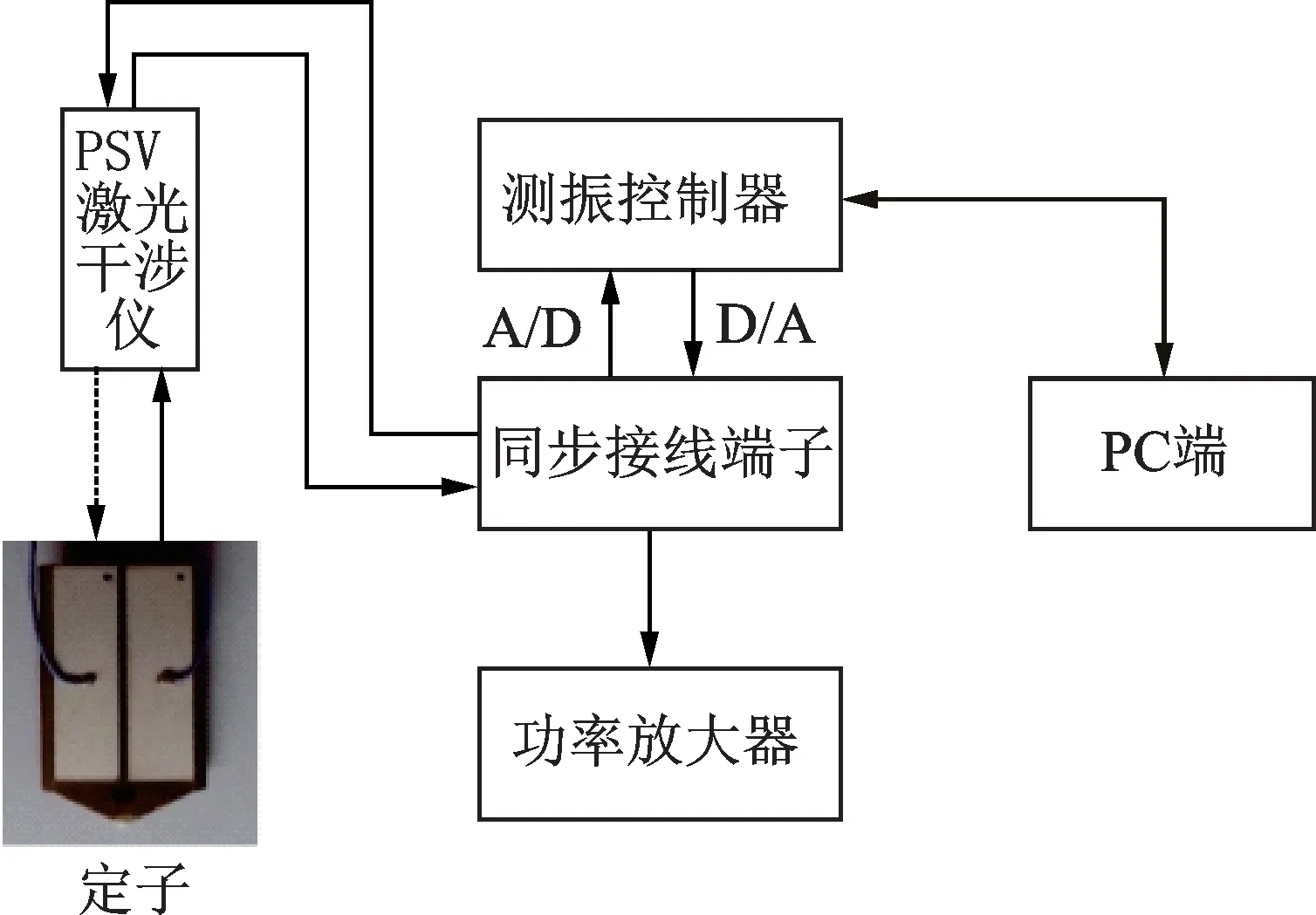
图3 多普勒测量系统原理图Fig.3 Principle diagram of Doppler measuring system

图4 为激光多普勒测振系统信号采集的原理示意图。电机定子在基准激励信号的作用下在振动平面产生振动。扫描激光器通过摆镜调整干涉仪发出的激光束，逐一测量振动平面上设置的测点。从测试点发射的激光束在扫描激光器中与基准激光束发生干涉并通过图像传感器记录干涉图像。该图像由振动测试仪中的解码器解析并输出正比于平行激光束振动速度的电压信号。

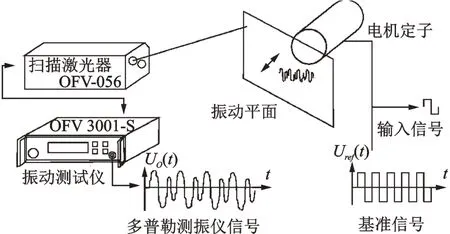
图4 激光多普勒测振系统信号采集原理Fig.4 Principle of data recording with a laser Doppler scanning vibrometer

多普勒激光测振系统测量时有以下要求，测量光束必须照射到被测表面，即只能测量垂直于测量表面的面外振动模态。由于上述电机定子工作在面内模态且结构为一空间多面体，多普勒面外振动测量系统无法直接获得定子整体的振动模态，进而识别其工作模态。下面分析如何在有限元分析的基础上合理地选择测量区域，从而实现该电机定子工作模态识别。

2 工作模态识别方法

2.1 面内纵振复合模态分析

为了分析上述面内纵振复合振动模态定子工作模态的特点，从而为提出工作模态的识别方法提供参考，基于商业有限元软件ANASYS建立了定子的有限元模型。定子各结构参数如图5所示，定子弹性体材料为磷青铜QSn6.5-0.2，压电陶瓷贴片为PZT8（长×宽×高为30 mm×8 mm×1 mm），所用材料性能参数如表1所示。有限元模型对实际定子做了两方面简化：忽略了粘接压电陶瓷和定子基体的胶层；将驱动足处的耐磨陶瓷珠简化为与基体同材质的尖角结构。

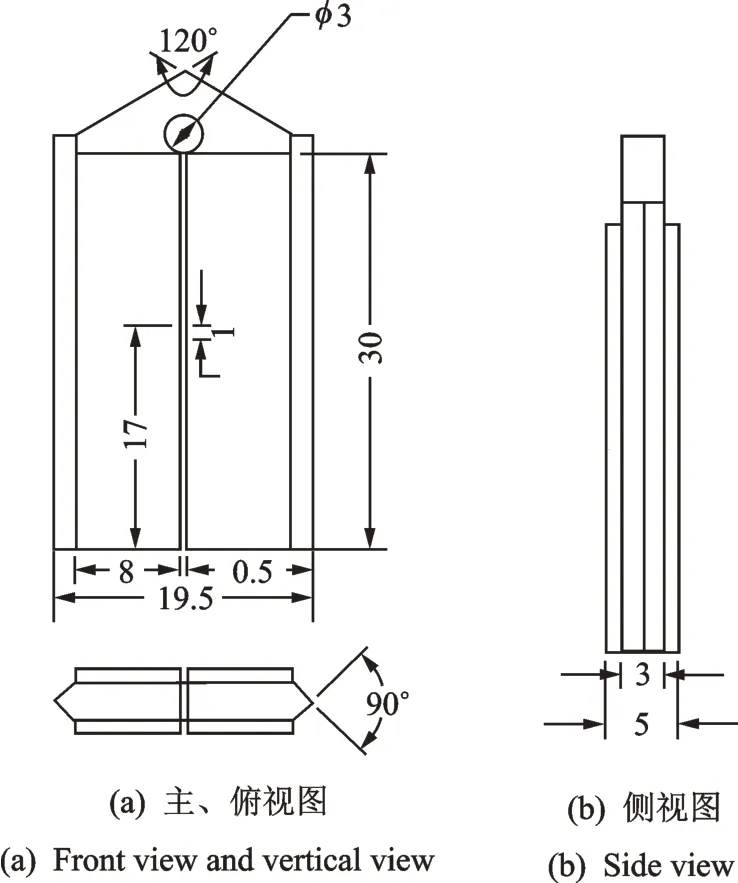
图5 定子结构示意图(单位:mm)Fig.5 Parameter diagram of stator structural(unit:mm)

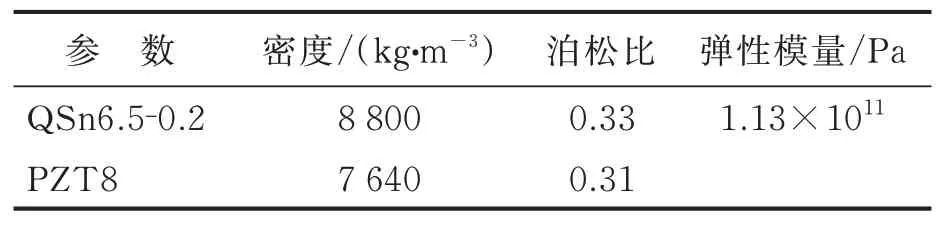
表1 材料参数Tab.1 Material parameters

压电陶瓷的刚度矩阵cE、压电矩阵e和介电矩阵εS如下

定子的结构在空间上具有两个对称面，因此，为了避免有限元模型网格不对称引起的失真，建立定子模型时首先建立了1/4定子的几何体模型，再对1/4定子模型进行网格划分，生成的1/4定子有限元模型通过镜像复制成为完整的定子有限元模型。有限元模型中采用了具有8个节点的三维耦合场单元solid5和映射网格划分了压电陶瓷部分几何体，其余金属体部分几何体采用具有塑性应变单元solid45单元和扫略网格。

根据ANSYS有限元分析软件对定子动力学建模，边界条件为设定为机械自由，压电陶瓷基板电势为零，设定频率范围为40 kHz～60 kHz，得到该定子的6个模态振型，仿真结果如图6所示，其中模态3，4两个工作模态分别为同相振动模态、反相振动模态，模态频率分别为54 456和54 848 Hz，其 余4个模态均不是所需要的工作模态。图中MAX表示振幅最大处，MIN表示振幅最小处。

根据模态分析得到振型云图，图6中模态3和4为工作模态。其中模态3为定子整体伸缩变形，振动的节面位于中部支撑结构处；模态4的振型表现为两侧分别伸长和缩短，由于两侧振子在中间有支撑结构并在端部相连，因变形协调关系，定子在整体上表现为弯曲变形，振动的节面同样也位于中部支撑结构处。因此，两个工作模态的应变最大的位置都位于中部支撑结构处，用于该电机工作模态振型的激励单元也设置在此处，以便获得良好的机电转换效率。

按图1所示的电激励方式给定子的4片压电陶瓷加上峰峰值200 V且相位差为90°的两相正弦和余弦电压信号，金属基体表面电势设置为零，得到其驱动足处的谐响应分析如图7所示。

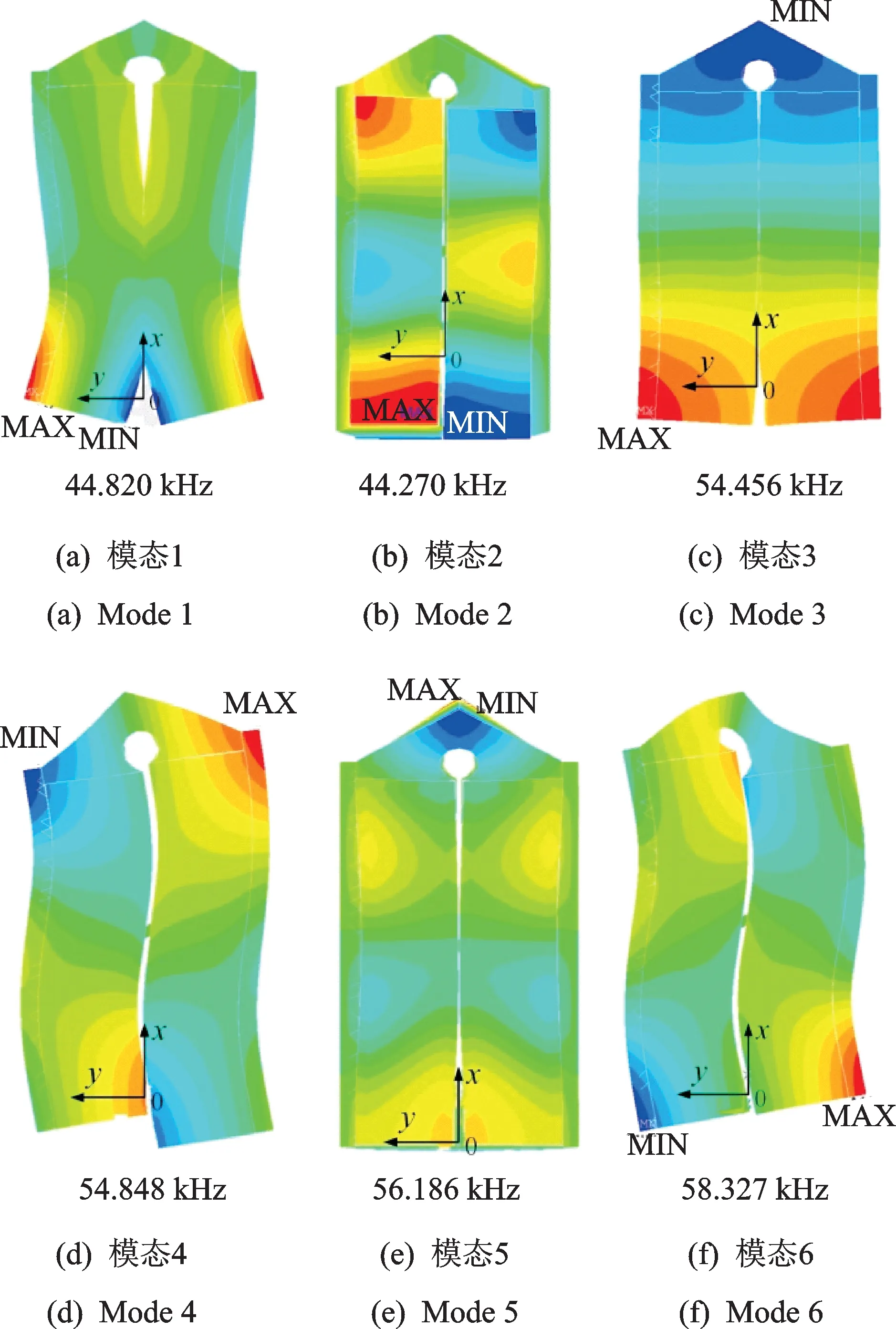
图6 工作模态及邻近模态振型云图Fig.6 Adjacent mode shape of working mode

图7 谐响应曲线Fig.7 Harmonic response curve

在该谐响应模型中，结构阻尼模型采用瑞利阻尼模型。若定子有限元模型的动力学方程可表示为

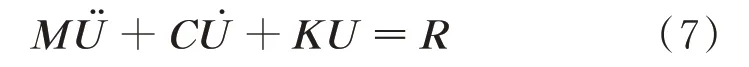
其中：M，C，K分别为模型的广义质量、阻尼和刚度矩阵；R为广义力矩阵；U¨，U˙和U分别为加速度、速度和位移向量。

有限元模型只计算广义质量和刚度矩阵，而广义阻尼矩阵由式（8）计算

其中：系数α和β由阻尼比ξ以及相应的振动频率决定，关系如下

根据经验值阻尼比ξ（0.003）和频率范围［ω1，ω2］可得α和β，频率范围包含工作频率的范围。

由图7可见，压电陶瓷在激励下使得定子能够同时有效地激发出工作模态（模态3为54.3 kHz，模态4为54.6 kHz）并且不引入其他模态，避免了干扰振动的出现，也能在模态实验过程中简化模态识别的工作。下面对定子模态的一般识别方法进行介绍，并针对上述定子的结构特点提出针对性的模态识别方法。

2.2 模态识别方法

定子工作模态频率附近存在干扰模态。为了将这两个工作模态从干扰模态中区分出来，引入振型相关系数MAC［19-20］（modal assurance criterion，简称MAC），来定量描述振型间的相似程度，用R来表示，其计算方法如式（10）所示

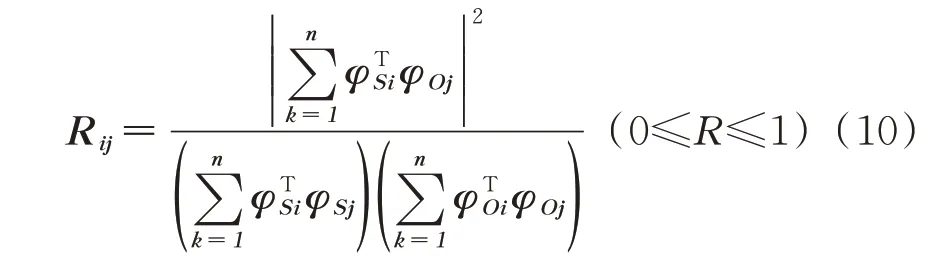
其中：φSi，i=1，2分别为工作模态4与工作模态5下 的 振 型；φOj，j=1，2，…，n分 别 为 各 阶 模 态 的振型。

由于定子结构的复杂性，实际模态实验中需要根据具体情况选择能够体现模态振型独特性且识别度高的测量位置。此外，因为多普勒测振仪只能测出平行于光路方向的振动，所选择的测量位置的振动方向要尽量与测量激光的传播方向一致，并且被测表面应尽量选择光滑平面以便得到更好的反射测量信号。根据上述原则，针对上述纵振压电振子的模态试验中选取定子底部端面为测量区域，并提取底部中线节点的两个工作模态下的振幅，并将其归一化处理，图8所示为工作模态的位移振型分布。

在上述定子的模态分析结果中，在定子底部中线均匀分布地选取数个节点，提取各个节点的模态形成振型矩阵，计算各阶模态的R值，计算结果如表2所示。

由表2中的各阶模态R计算数值可见，根据振型相关系数R值，可以将谐响应分析中的两个工作模态有效地识别出来。虽然对同相振动模态R计算时3阶和5阶模态振型的R接近，但是在对定子进行谐响应分析时不会激发5阶振型，因此通过上述方法可以有效分辨上述纵振复合模态定子的工作模态。

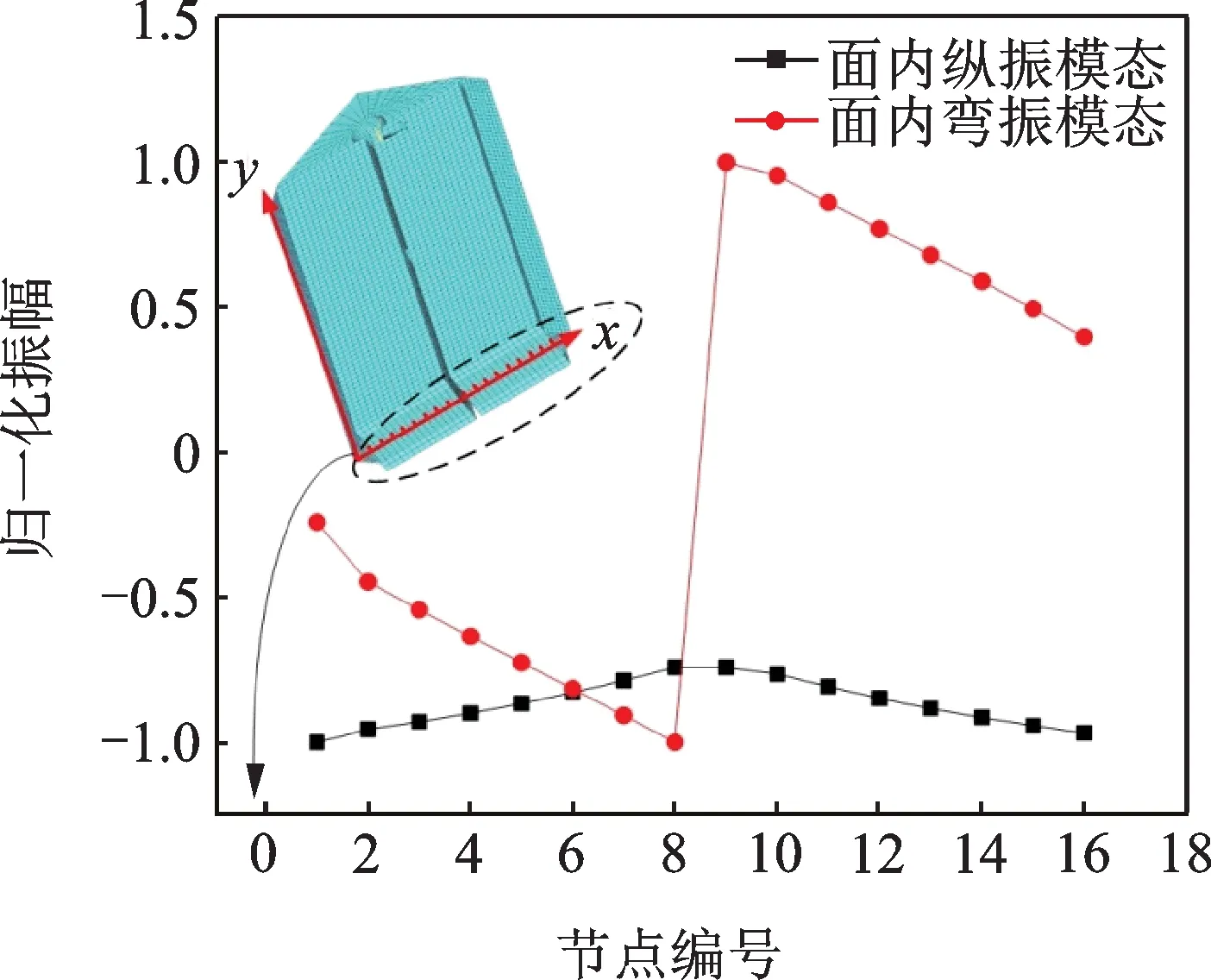
图8 测量节点示意图及其振型分布Fig.8 Measuring the mode distribution of nodes

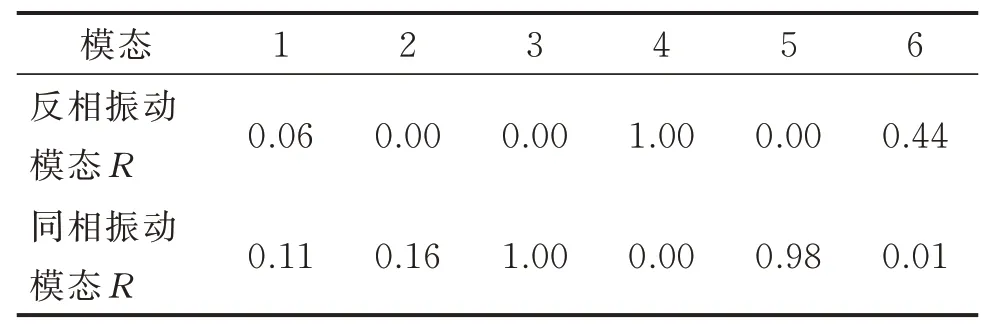
表2 各模态R值Tab.2 R value of each mode

3 试验与结果讨论

3.1 试验装置

研究者根据有限元模型的结构参数加工了定子样机，在陶瓷片中间位置附近焊接导线。有限元仿真结果表明，该位置靠近振型节面，对定子的固有特性影响相对较小。图9为PSV-300F-B型激光多普勒干涉仪测振系统，该系统由PSV激光干涉仪、测振控制器、同步接线端子、功率放大器和计算机组成。其中：PSV干涉仪由摄像机、干涉仪和摆镜构成；测振控制器将干涉仪的干涉图像信息解码为与振动速度成正比的电压信号；计算机通过数据采集卡获取振动信息并根据用户需要进行显示，还可对测试模式进行设定［21］。

图9 模态测试试验装置Fig.9 Experimental equipment for modal testing

3.2 试验结果

根据对定子结构特性及振动模态的分析，选取定子底部整个被压电陶瓷所粘接的金属基体的矩形区域为激光测振仪的扫描表面，如图10所示，黑色网格部分为测量区域。

图10 模态试验测点网格图Fig.10 Mesh diagram of modal test points

图11 所示为定子底边的扫描振型，对定子的底部端面进行振动测量，可以观察到在整个扫描频率范围内，有多处峰值，定子的多个模态被激发，在55 953 Hz处发现其同相振动模态，在55 391 Hz处发现其反相振动模态。

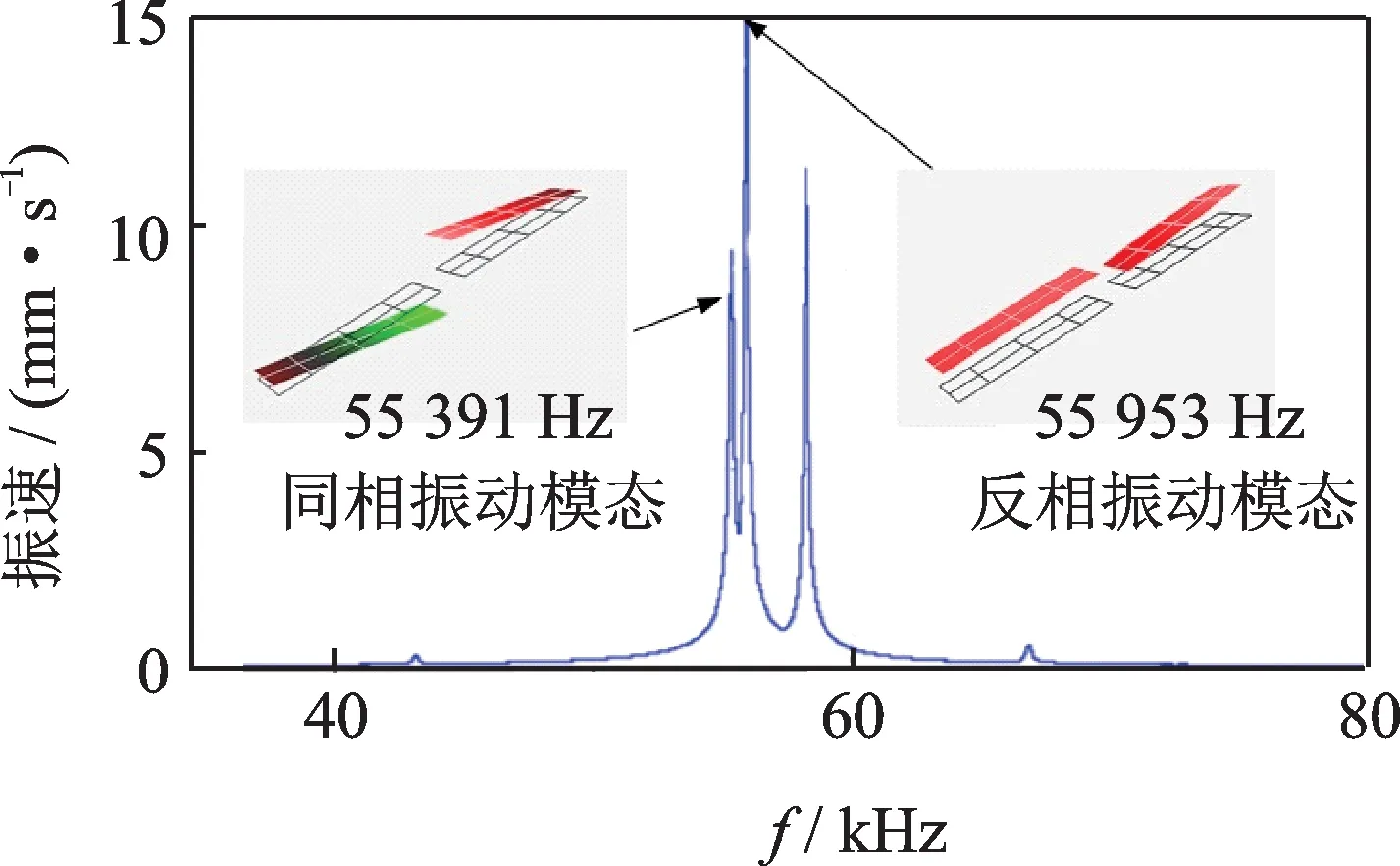
图11 多普勒测振扫描曲线Fig.11 Harmonic scan with Doppler vibrometer

3.3 分析与讨论

根据利用Ansys有限元仿真软件仿真得到该定子两振动模态下的频率差为392 Hz，与试验结果测得的频率差562 Hz存在差异，分析其原因主要有：①在仿真时忽略了实际制成样机的工艺带来的误差，如用于粘接金属基体与压电陶瓷贴片之间的环氧树脂胶层的影响，而胶层的刚度小于金属基体及压电陶瓷的刚度；②仿真时对定子驱动足进行简化。实际样机中的驱动足为球形的胶体接触，与金属基体通过胶粘为一体，在ANSYS有限元仿真时未考虑驱动足的形状及与弹性体的连接工艺，以尖头建模计算；③不可避免的制造误差以及设计尺寸时的形位公差，导致实物尺寸与仿真时尺寸存在微小差异。

模态测试结果表示，除面内纵振模态与面内弯振模态两个工作模态外，还发现另一个峰值，据有限元仿真结果可知，该峰值驱动足处不发生x方向以及y方向的移动，所以不是人们所需要的模态，属于干扰模态。

4 结束语

本研究在介绍一种纵振复合模态直线超声电机的工作原理的基础上，对其工作模态分析，通过提取定子工作模态振型并根据振型相关性以及激光多普勒测试的特点，提出了通过局部振型的相关性比较实现其工作模态识别的方法。定子动力学仿真结果以及对定子底端局部模态振型的测量结果都表明，通过利用多普勒激光测振仪对定子底部局部振型的测量，可以识别该定子的两个工作模态。该方法可以推广应用于由一对纵振模态复合的超声振子的工作模态识别，还可以更高效地从有限元分析得到的多个模态分析的结果中找出工作模态，为结构的动力学优化奠定基础。