车内噪声主动控制系统鲁棒性分析与优化∗

张立军， 张希玉， 孟德建

（1.同济大学汽车学院 上海，201804）（2.同济大学智能型新能源汽车协同创新中心 上海，201804）

引言

主动噪声控制的应用和研究中，系统鲁棒性是非常关键的一个研究点。在车内噪声主动控制中，由于汽车行驶工况复杂、使用特性多变，使得其对系统鲁棒性的要求更加严苛。这也是主动噪声控制系统在汽车应用发展缓慢的一个重要原因。

在主动噪声控制领域，Bai等［1-2］运用鲁棒控制理论，解决许多诸如管道、封闭声场及头戴耳机等噪声主动控制的鲁棒性问题。文献［3-4］分别利用仿真方法，证明了鲁棒控制相较于滤波最小均方误差算法，在不稳定噪声的控制中具有更好的效果。李普［5］将这一思想移植到声振主动控制中，取得较好的效果。为了消除次级通路不确定性的影响，Thai等［6］提出了一种基于步长自适应和次级通路分解的无次级通路估计主动噪声控制模型。王进军等［7］提出了基于H∞鲁棒性控制理论的有源控制器设计，有效克服了次级通路不确定性所引起的问题。Montazeri等［8］设计了一种自适应无限冲击响应滤波器的主动声振控制系统，使用改进的自适应算法使得系统有较好的稳定性。Zhang等［9-10］则应用在线建模方法，通过添加白噪声激励对次级通路进行实时辨识更新，但此法很难满足实时性要求。Davari等［11］提出了一种基于新版本的滤波最小均方误差算法的次级通路建模方法，通过仿真表明该方法对于次级通路模型的瞬变具有很强的鲁棒性。Kim等［12］提出了一种用来估计次级通路定步长的归一化最小均方误差算法，仿真表明该方法提高了收敛速度，降低了稳态误差。

上述文献提出了多种提升次级通路鲁棒性的方法，但均未涉及多通道自适应陷波系统鲁棒性的研究。在车内噪声主动控制系统中，由于乘员状态、车窗开闭以及车辆行驶工况等汽车使用情况的多变性，导致系统中存在很大的不确定性。因此，急需对多通道自适应陷波的车内噪声主动控制系统的鲁棒性展开深入研究。

笔者首先建立了多通道自适应陷波的车内噪声主动控制系统的离散状态空间模型，定义了收敛率和稳态误差增益来刻画系统的降噪性能；其次，分析了导致系统不稳定的外在因素，并将其归结为次级通路鲁棒性问题，基于理论推导，对此鲁棒性问题进行了深入的分析。还就次级通路鲁棒性对系统收敛性的影响，以及次级通路完全失配的边界条件进行了理论分析，并对分析结论开展了实验验证；最后，基于分析结果对次级通路估计进行优化设计，大幅提升系统的收敛性，并分析了次级通路反馈和泄露算法两种方法来改善系统的鲁棒性。

1 车内噪声主动控制系统模型

图1 为多通道自适应陷波车内噪声主动控制系统框图。考虑分析的普适性，假设系统包含M个麦克风和N个扬声器，需要控制P个频率成分的噪声。

图中d(n)为初级噪声，假设其仅含P个待控制的谐波成分；y(n)为自适应陷波器输出矢量；s(n)为麦克风输入矢量；e(n)为系统误差矢量；x(n)为参考信号矢量，其变形后得到参考信号矩阵X(n)；Hs为N×M维的次级通路传递函数矩阵；Hˆs为次级通路传递函数矩阵的估计；w(n)为自适应陷波器权系数矢量，是由最小均方误差算法（least mean square，简称LMS）实时计算得到。

图1 多通道自适应陷波算法Fig.1 Multi-channel adaptive notch filter algorithm

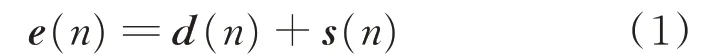
根据最速下降法可知权矢量的迭代公式为

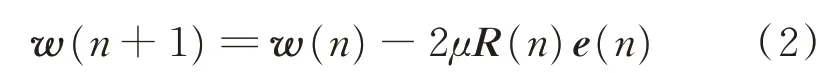
其中：μ为收敛系数；R为滤波参考矩阵，可表示为

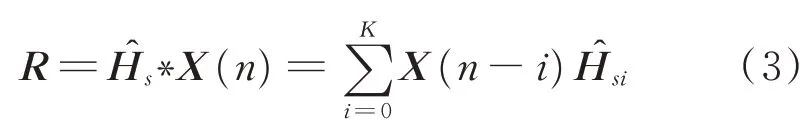
为了降低运算量，利用离散傅里叶变化对式（3）进行简化，定义

则式（3）可以转化为

1.1 次级通路鲁棒性的离散状态空间方程

根据最小化均方误差原理，定义目标函数为

假设当J达到最小值时，w(n)≡wo，令

通过化简可得

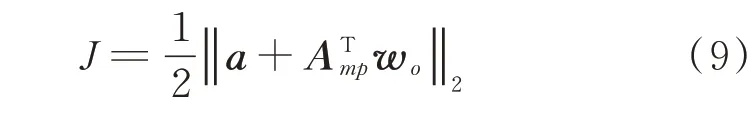
定义Δw(n)=w(n)-wo，则有

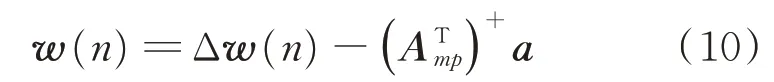
将式（1），（6），（7）带入式（10），进一步简化得到

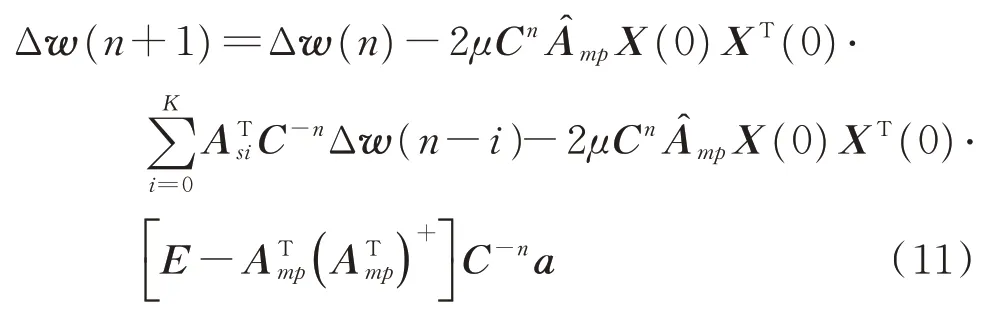
为了进一步简化表达式，定义则收敛方程可以简化为

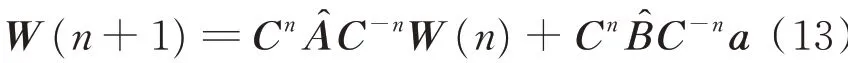
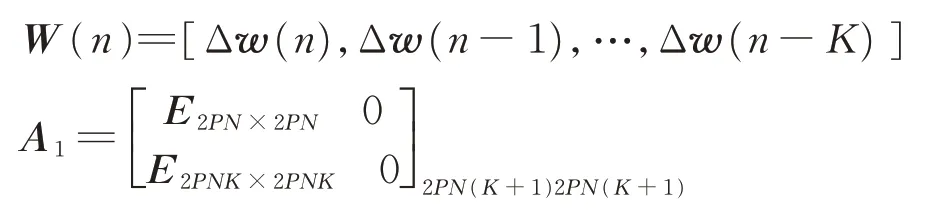
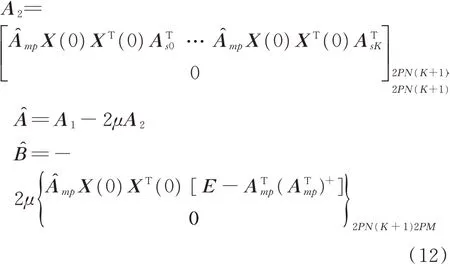
通过坐标变换把它变成一个时不变系统

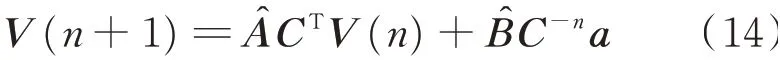
为自适应陷波算法次级通路鲁棒性问题等价离散系统状态空间方程。

同理可以得到其输出方程为

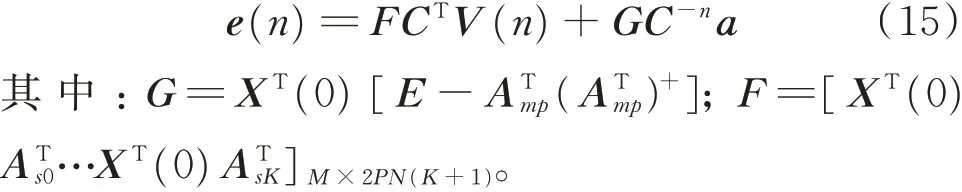
自适应陷波算法次级通路鲁棒性等价离散系统状态空间方程为

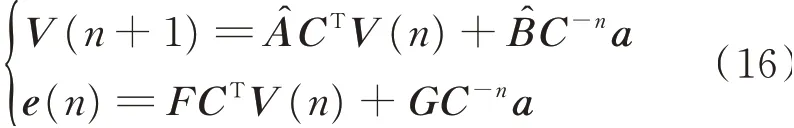
1.2 系统降噪性能评价指标

为了对系统的降噪性能进行量化评价，定义收敛率和稳态误差。假设控制系统的目标函数J=0。此时，满足条件a=-Ampwo，将其带入式（14），结合式（8），（11），（12）将其化简得到

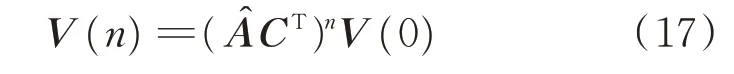
这里假设AˆCT可以对角化，存在可逆矩阵D与对角阵使得AˆCT=D-1ΛD。将其带入式（17），并在等号两边取二范数得到并由二范数定义和范数相容原理可以推导得到

其中：ρ(⋅)为矩阵的谱半径。

由式（18）可以看出，系统指数收敛。进一步推导得到收敛性与时间t和系统采样频率fs的关系为

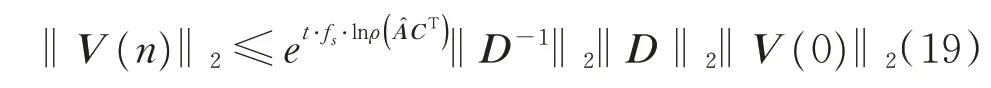
根据式（19），定义该系统的收敛率α为

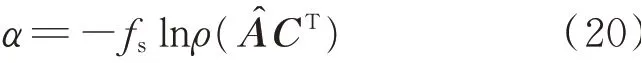
当α＞0，系统收敛，且α越大，收敛时间越快。为了更加直观反映系统收敛速度，定义时间常数τ

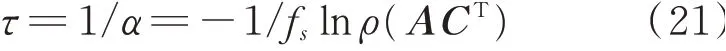
其物理意义是，收敛曲线在0点的切线与时间轴的切点如图2所示。当过去τ时刻以后，系统可以收敛到37%；当过去3τ时刻，系统可以收敛到5%，一般此时认为系统已经完全收敛完毕，因此把3τ称为系统的收敛时间。

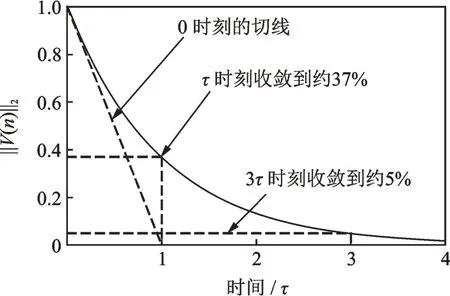
图2 时间常数Fig.2 Time constant

假设系统收敛时，系统的状态空间V（n）满足

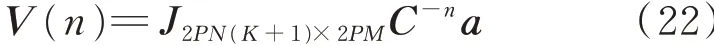
其中：J为一个待定矩阵。

将该假设带入系统的状态方程内，求取待定矩阵J，将其代入系统输出方程式（15）中，获得系统收敛时的稳态误差为

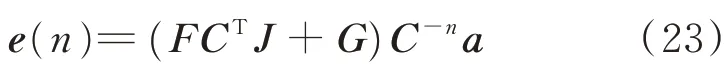
定义

为自适应陷波器的稳态误差增益。显然，β越小，则系统对车内噪声的抑制作用越好。化简得到稳态误差和稳态误差增益为

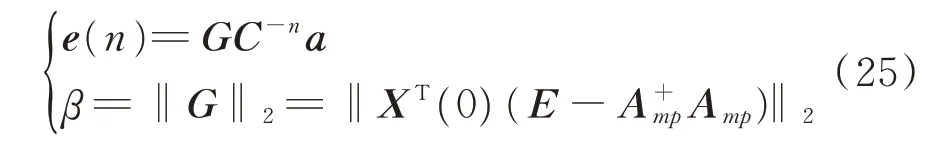
由范数相容原理可以得到

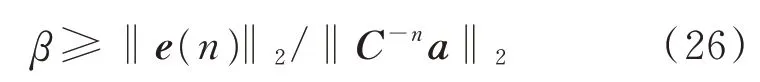
不等号的存在，使得无法通过仿真的手段计算β的值，只有利用式（26）通过理论计算的方法，才能客观评估系统稳态误差的性能。

2 次级通路鲁棒性分析

2.1 次级通路鲁棒性

图3 点划线框内是系统控制器，点划线框外是被控声学系统和传感通信部分。显然，系统鲁棒性问题主要是由点划线框外的不确定性引起。本研究主要分析由次级通路不确定性引起的系统鲁棒性问题。根据控制系统框图可以看出，由次级通路引起的鲁棒性问题主要包括：①次级通路估计误差；②误差信号传感器的传递函数及其变化。

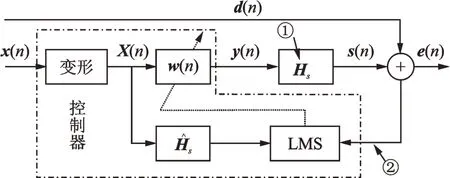
图3 自适应滤波器示意图Fig.3 Schematic diagram of adaptive filter

2.2 次级通路鲁棒性影响因素

由式（25）可以看出，当系统完全收敛时，稳态误差增益β中不包含次级通路估计项，也就不存在次级通路的估计误差问题。由式（20）可以看出，系统的收敛率α中包含了次级通路的估计项。为了分析次级通路鲁棒性对系统收敛性的影响，下文将用试验和仿真相结合的方法来对其进行深入分析。

车内噪声主动消声试验平台以dSPACE实时仿真系统为核心，对外围的软硬件进行合理配置，如图4所示。本研究硬件在环平台包括MicroAutobox、扬声器系统和麦克风模块。使用的扬声器为原车的4个车载扬声器，麦克风使用了市售的OCROBOT麦克风模块。

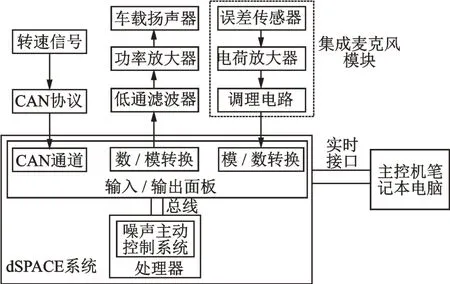
图4 快速控制原型试验平台Fig.4 Rapid control prototype test platform

以发动机3 900 r/min的2阶噪声为控制目标的4扬声器4麦克风配置系统为例，通过实车试验标定标准工况（车内仅有驾驶员，且车窗全部关闭）、右后排一人工况、车窗全开工况、仅右前窗关闭工况的次级通路传递函数，并假设标定的传递函数为真实传递函数，即不考虑试验误差。然后，运用式（20）计算不同的次级通路导致的系统收敛率随自适应算法收敛系数的变化情况，计算结果如图5所示。

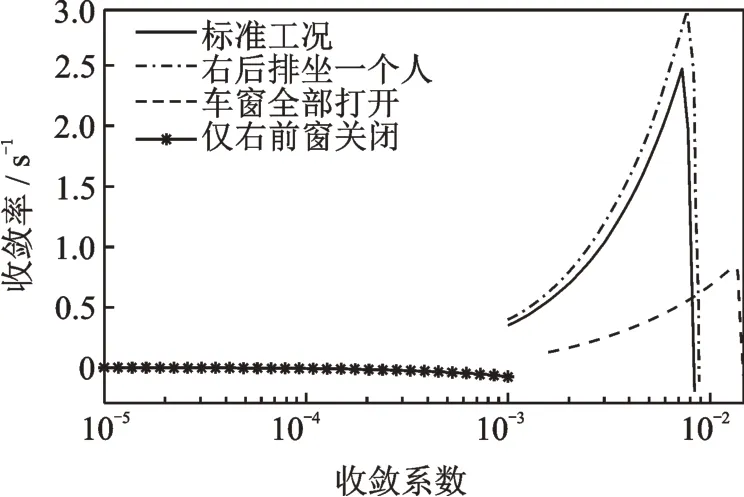
图5 收敛率随次级通路估计的变化Fig.5 Convergence rate changes with secondary path estimates

从图5可以看出，当次级通路改变时，系统的收敛率、最优收敛率和最优收敛系数都发生了变化。其中，右后排一人工况的收敛率与最优收敛率都有所提升。说明次级通路的改变并不是一个坏事。但是，仅右前窗关闭工况中，无论收敛系数如何改变，系统都不会收敛。说明此时只改变系统的收敛系数，已经完全无法使系统产生降噪效果，这种情况称之为次级通路完全失配现象。

为了进一步研究次级通路完全失配发生的条件，文中定义：若存在最大收敛系数μmax＞0，使得若收敛系数满足0＜μ＜μmax，系统收敛率均有α＞0，则定义这种系统是可以收敛的；若找不到这样的μmax，则定义这种系统完全不可能收敛，或称这种系统存在次级通路完全失配现象。

2.3 次级通路完全失配的边界条件

对于单通道系统，当次级通路与次级通路估计的相位差超过90°时，产生次级通路完全失配现象［13］。但是，这种方法不适用于多通道算法。一个N扬声器M麦克风的自适应陷波器，共有N×M条次级通路。其中1～2条次级通路的相位差超过90°，并不一定会导致次级通路完全失配现象。为了得到多通道自适应陷波系统的次级通路完全失配的边界条件，下面将借助理论推导方法对其进行分析。

假设系统没有稳态误差，则自适应陷波算法的收敛方程可以变为

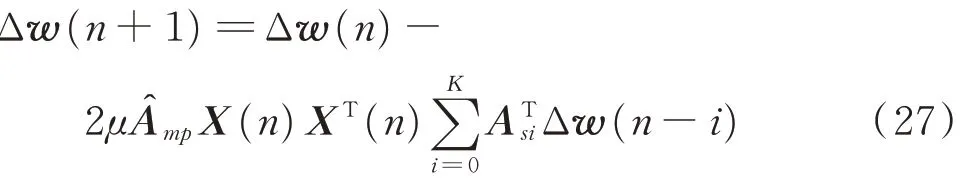
当收敛系数μ非常小，则收敛过程非常缓慢，可以认为Δw(n-i)≈Δw(n)，用E[X(n)XT(n)]替代X(n)XT(n)，并对Aˆmp ATmp进行特征值分解

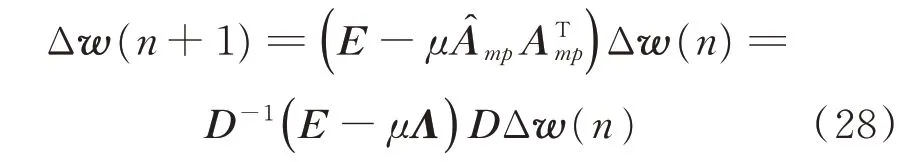
其中：Λ=diag(λ1，λ2，…，λ2PN)。

显然，只有当

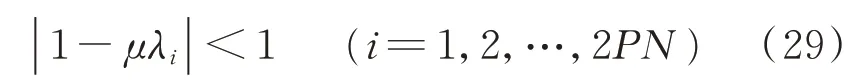
时，线性离散系统才是收敛的。由于μ非常小，可以进一步认为当Re(λi)＞0（i=1，2，…，2PN）时，系统是收敛的。

若有一个特征值向量指向复平面实值为1的竖线右边，那么调整收敛系数，无法确保系统所有极点都落到单位圆内，导致次级通路完全失配现象的出现。

通过以上分析可以看出，在实际操作中，可以通过取一个极小的收敛系数μ，计算系统的收敛率。若在此极小的收敛系数下系统收敛率仍为0，那么一般情况下系统是不可能收敛的，即发生了系统次级通路完全失配的现象。

为了验证文中分析结果的正确性，这里以上文标定的工况对结果进行校验。计算仅右前窗关闭工况Aˆmp ATmp最大特征值随频率的变化。如图6所示，曲线在130 Hz附近超过90°，所以从理论上系统在这个频率上出现次级通路完全失配现象。而130 Hz对应发动机3 900 r/min时的2阶噪声频率，这与计算的工况完全匹配。

同样，对其他3个工况计算其特征值，结果如表1所示。从标准工况可以发现，如果不存在次级通路估计误差，则系统特征值相角计算结果全部为0。对比标准工况与右后排坐一个人的工况发现，后者最大的相角不大，但是最大特征值与最小特征值的幅值比有所减小，这表示通过调整收敛系数μ可以让其都更加接近0点，因此后一种工况可以到达更高的收敛速度。对比标准工况与车窗全部打开的工况发现，虽然后者特征值幅值比更加小，但是特征值普遍与x轴夹角较大，所以系统更加不容易收敛。综上，如果不考虑系统的延迟，当

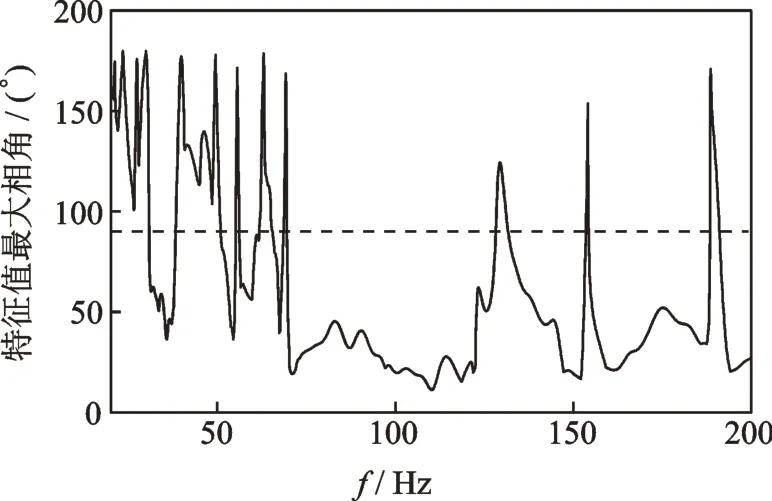
图6 最大相角差随频率变化情况Fig.6 Maximum phase angle difference with frequency

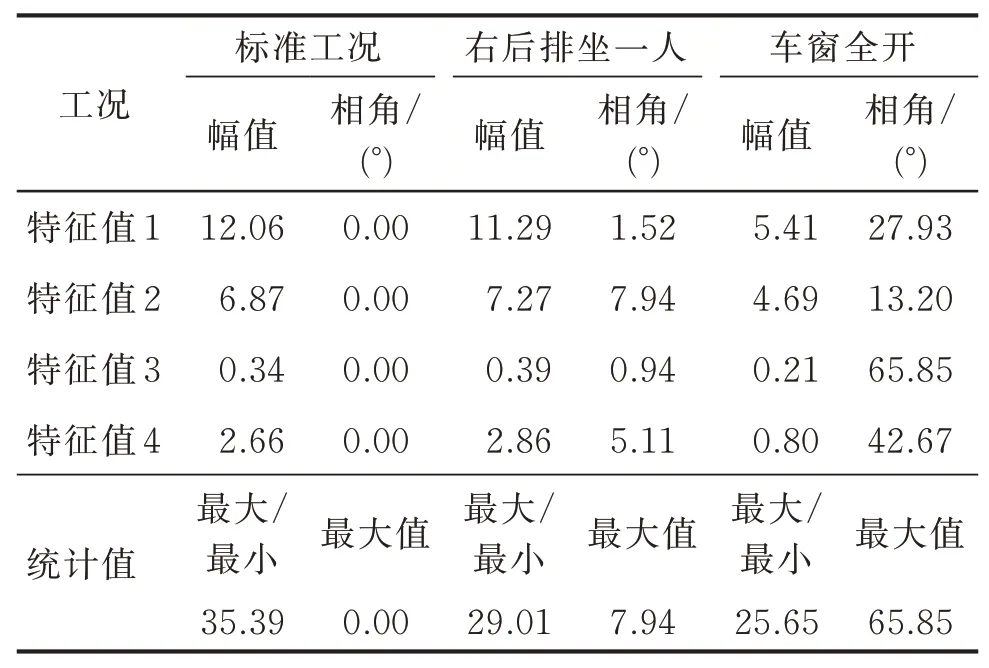
表1 工况特征值统计Tab.1 Statistics of eigenvalues of different working conditions

3 次级通路鲁棒性优化和改进

3.1 面向收敛速度的次级通路估计优化

为了提升系统的收敛速度，可以根据上文分析结果式（30）对次级通路进行设计优化。显然，当设计

时，系统的收敛速度将发生大幅度提升。这里仍以控制130 Hz目标噪声的4扬声器4麦克风系统为例，分析结果如图7所示。在次级通路估计优化前，系统最快的收敛率约为2.5，但是经过次级通路估计的优化，系统的收敛率超过了11.6。这从理论上说明这种优化方法可以提高多通道系统的收敛速度。

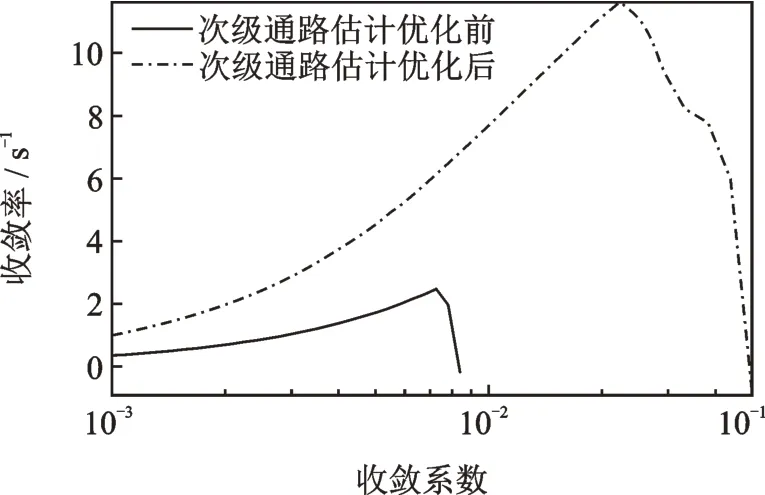
图7 次级通路估计优化效果Fig.7 Effect of secondary path estimation optimization

为了进一步验证上面的优化结果，以4扬声器4麦克风系统怠速3 000 r/min静止工况为例，通过实车试验验证改进次级通路对于系统降噪性能的影响，结果如图8所示。实际收敛的曲线斜率与理论计算获得的收敛曲线斜率基本相同，验证了算法收敛速度估计方法的准确性；使用了改进的次级通路估计以后，系统的收敛速度大幅提升，验证了上述优化结果的正确性。

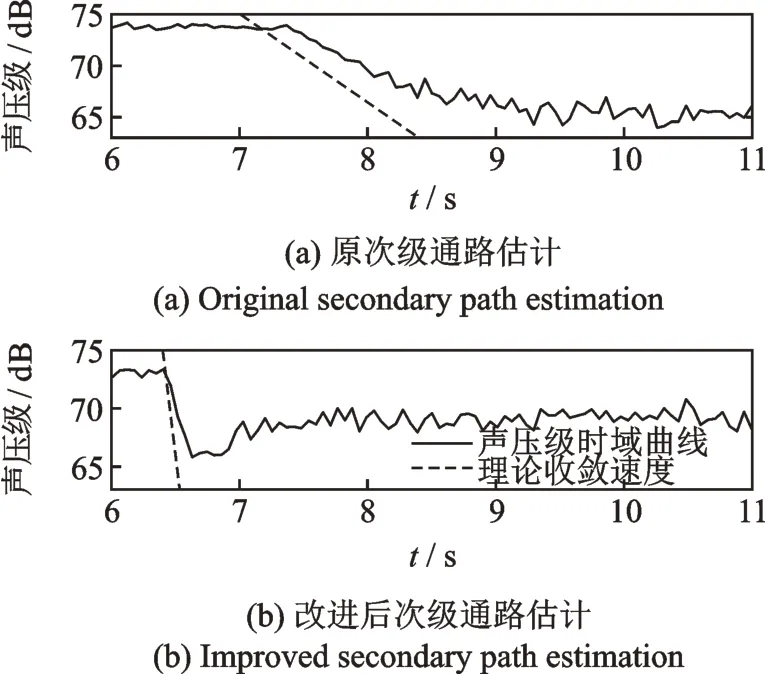
图8 次级通路估计对收敛速度的影响Fig.8 Impact of secondary path estimation on convergence speed

虽然这种优化方法可以大幅提升系统的收敛性，但不会提高系统的次级通路鲁棒性。如图9所示，使用优化的次级通路估计以后，系统仍然会发生次级通路完全失配现象，发生完全失配现象的频率并没有因为改进算法以后而减少。

3.2 次级通路鲁棒性抑制——次级通路反馈

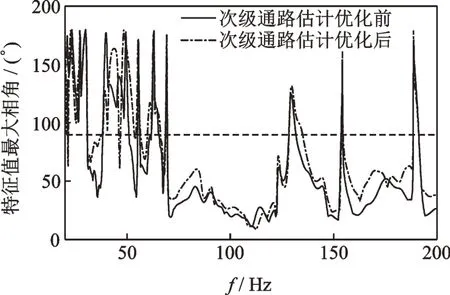
图9 次级通路估计对系统鲁棒性的影响Fig.9 Effects of secondary path estimation on the system robustness

为了解决自适应滤波算法的次级通路鲁棒性问题，赵剑等［14］提出在次级通路回路上增加一个固定系数反馈控制器，以减小次级通道的不确定性［14］。在自适应陷波算法中，也可以采用相同的方法提升系统次级通路鲁棒性。具体是在次级通路旁并联一个反馈控制器，将误差信号传感器采集到的信号反馈回到系统的输出。此时，系统的误差矢量e（n）和新的次级通路传递函数变为

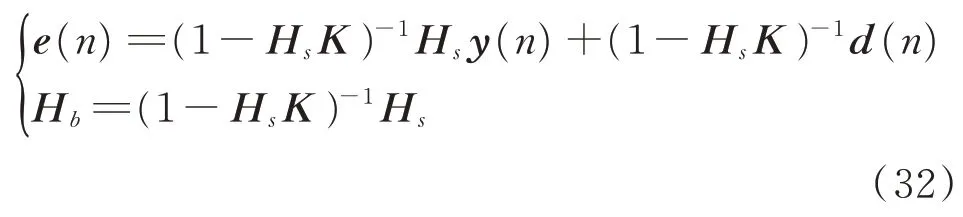
对Hb求导，根据Woodbury求逆公式，化简可得

由式（33）可知，如果能够设置控制器K，使得越小，新系统抑制次级通路变化的能力越强。可以证明(1-Hs K)-1与(1-KHs)-1拥有相同的不等于1的特征值。同时，根据谱半径ρ(A)≤‖A‖这一特性，可以得到

若希望dHb尽可能小，则需要设计控制器K使得ρ(1-Hs K)尽可能大。若不计初级噪声d（n），误差项可以写成

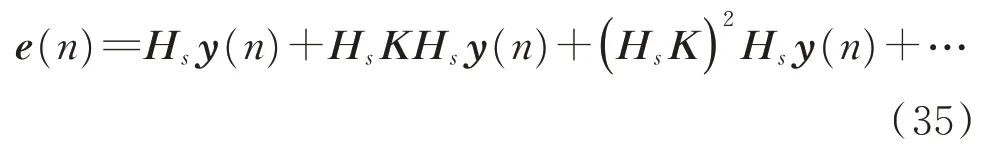
的等比数列，因此不难获得，系统稳定的条件为等比系 数ρ(Hs K)＜1。实 际 设 计 时，可 以 先 给 定γ∈(0，1)，并设计控制器

即满足设计要求。γ选择越小，系统的次级通路鲁棒性越差；γ选择越大，则反馈系统内部的稳定性越差，系统越是容易发散。式（36）获得的K是一个M×N阶的复数矩阵，每个元素kij对应一个在某一频率上满足一定幅值相位特性的滤波器。选择将元素kij转换为一个二阶滤波器，即

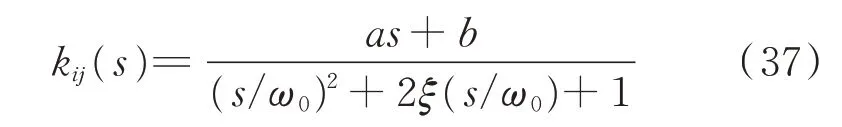
其中：传递函数的分母为一个二阶震荡环节；ω0为自适应陷波系统需要控制的角频率；ξ为震荡系统的阻尼比，阻尼比取很小；传递函数的分子是一个一阶微分环节，用来使得整个滤波器的传递函数等于kij。

传递函数功能是将所控制的频率过滤出来，避免初级噪声d中ω0以外频率成分的噪声的传递函数满足ρ(Hs K)＞1，使得反馈系统发生不稳定。

同样用上节所分析的4个扬声器4个麦克风系统为例进行分析。如果不使用次级通路反馈，系统必然发散。根据系统130 Hz的次级通路传递函数设计反馈控制器K，令γ=0.8，ξ=0.01。对新的系统进行仿真，仿真结果如图10所示。图中麦克风1～4分别对应车内左前、右前、左后和右后4个位置，实线为降噪前的声压，虚线为降噪后的声压。

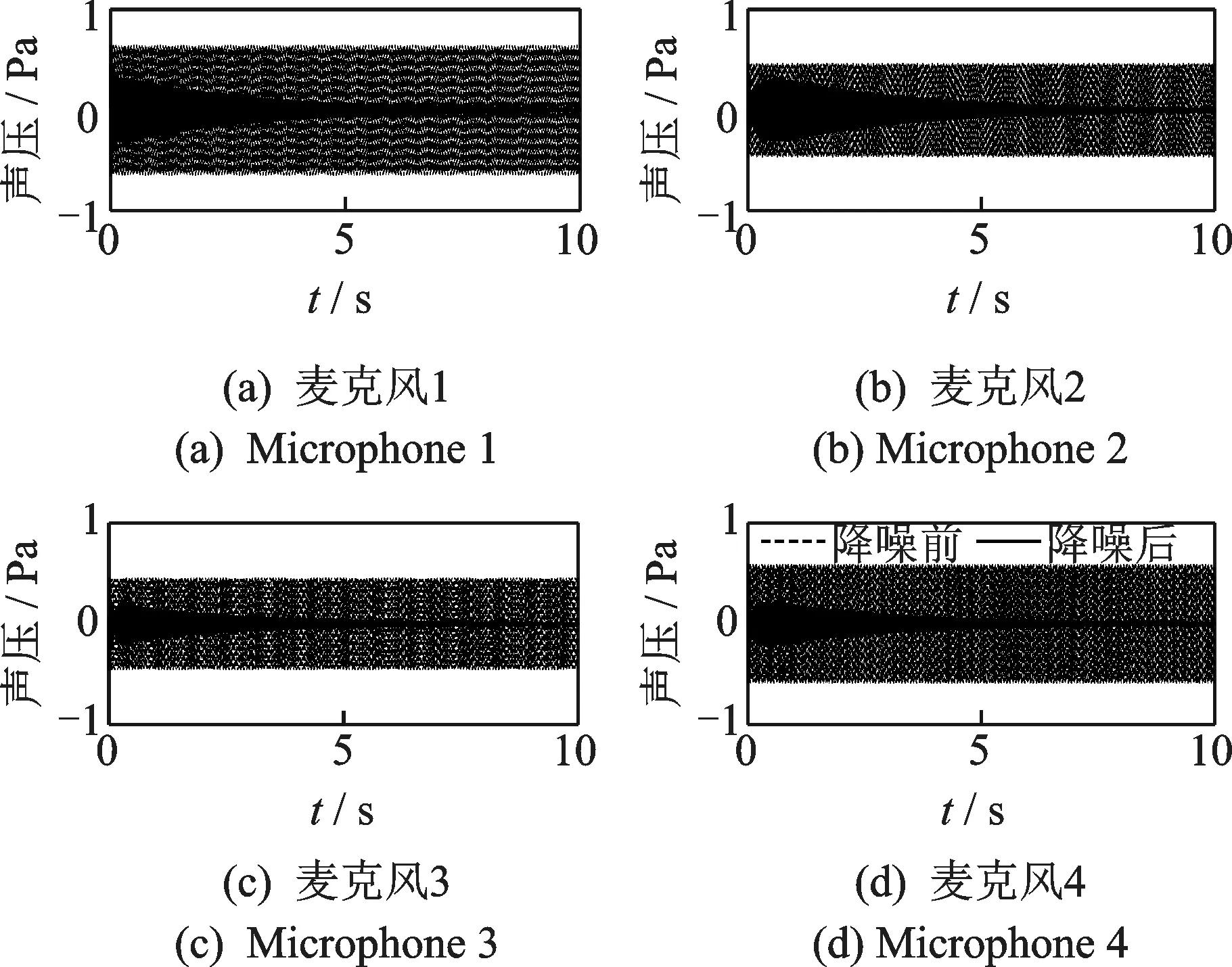
图10 次级通路反馈的控制效果Fig.10 Control results of secondary path feedback

结果表明，次级通路反馈方法在提升系统次级通路鲁棒性的同时，仍然可以保障稳态误差为0，这使其拥有更好的降噪效果。除此以外，从式（32）可见，如果关闭自适应陷波器，那么系统的输出为

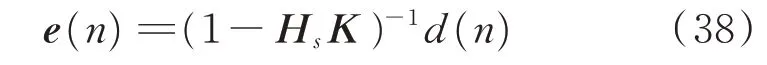
由于设计‖(1-Hs K)-1‖很小，所以系统对初级噪声d仍然有削减的作用，此时这个反馈控制器成为了一个非自适应反馈控制的主动噪声控制器。系统不打开自适应陷波器时的降噪性能如图11所示。可以看出，这个反馈控制器也具有很好的降噪效果。降噪效果的好坏同γ的取值有关，γ越大，则系统的降噪效果越好。

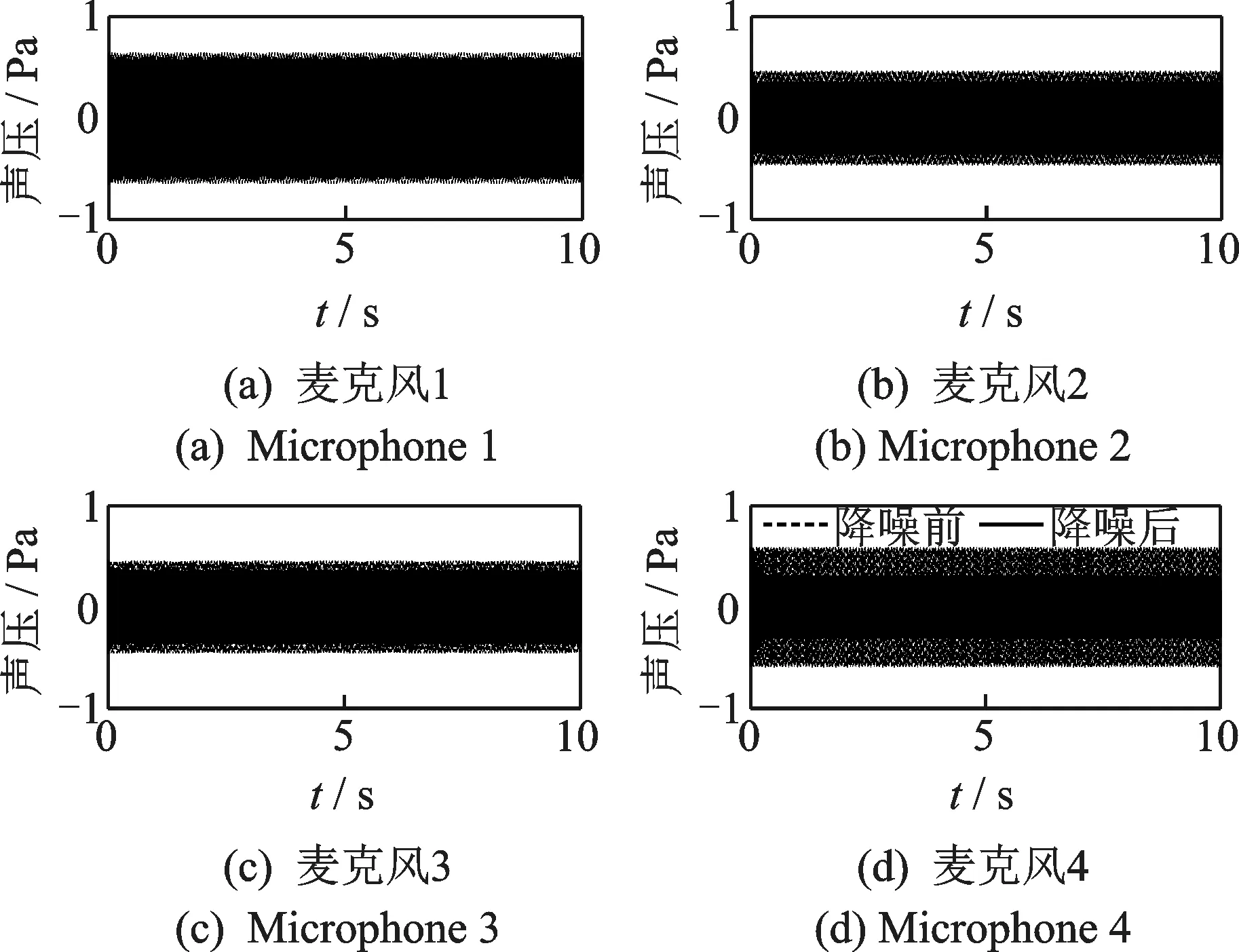
图11 关闭自适应陷波器后的控制效果Fig.11 Control results after closing the adaptive notch filter

由此可见，次级通路反馈的方式相比泄露算法，具有稳态误差为0、具有非自适应降噪能力等优点，但是当次级通路的变化dHs过大，系统仍然可能发生次级通路完全失配现象。图12所示，随着γ的变大，特征值最大相角绝大部分情况下下降了，这说明次级通路反馈的确提高了系统的次级通路鲁棒性。但是，仍然有一部分相角在90°以上，也就是说系统仍然存在次级通路完全失配的风险。

图12 次级通路反馈对特征值最大相角的影响Fig.12 Effects of secondary path feedback on the maximum phase angle of eigenvalues

综上，次级通路反馈方法不能彻底解决次级通路完全失配现象，尤其是对于车内噪声这种次级通路变化范围大、频率范围宽的系统。

3.3 次级通路鲁棒性抑制——泄露算法

为了保证次级通路的鲁棒性，自适应陷波算法的控制目标中还需要约束次级信号的大小，即

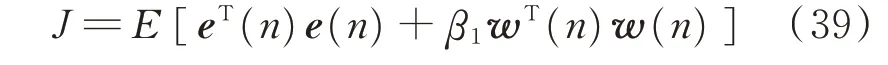
其中：β1为泄漏量。

根据最陡下降法原理得到泄露自适应算法的权矢量迭代公式为

其中：ν=1-2μβ1为泄露因子，其取值越大，系统的次级通路鲁棒性越好，但是系统的稳态误差越大。

以4扬声器4麦克风为例进行分析，次级通路估计的是驾驶员仅1人、车窗全部关闭的情况，但是真实的情况是只有右后排的车窗是关闭的。系统消除发动机3 900 r/min对应的2阶噪声。图13是使用一般算法时系统的降噪效果，取收敛系数μ=10-2，可以明显发现系统处于发散状态。

图13 一般算法的降噪效果Fig.13 Noise reduction of the general algorithm

但是如果加入泄漏量β1=0.1，由图14可以看出，系统可收敛，但有一定稳态误差。

图14 泄露算法的降噪效果Fig.14 Noise reduction of the leak algorithm

泄露算法在稳态误差和稳定性之间存在矛盾，所以希望在系统稳定的前提下，让泄漏量越小越好。

为了分析系统次级通路鲁棒性，统计了以车窗全关为估计工况，所有开关窗情况下Aˆmp ATmp特征值最大相角的变化情况，工况代号分别表示左前、右前、左后与右后车窗的开闭情况，1代表开窗，0代表关窗。统计结果如图15所示。

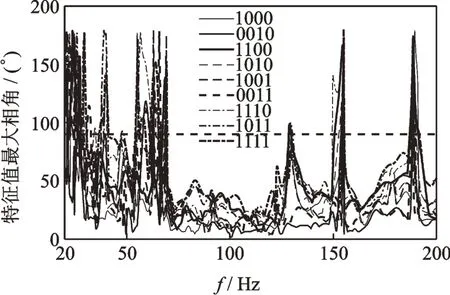
图15 次级通路鲁棒性统计结果Fig.15 Statistics of secondary path robustness

统计发现，次级通路完全失配现象并不是在任何频率下都有出现的风险，容易出现次级通路完全失配现象的区域包括70 Hz以下、130 Hz附近、150～155 Hz附近、190 Hz附近。在这些区域可以适量设置泄漏量，而在其他次级通路完全失配风险较低的地方，可以设计泄漏量β1=0，以减小稳态误差，提高系统的降噪性能。

以4扬声器4麦克风系统为例，试验验证算法的可行性。工况为1 000 r/min静置，由图16可见，该工况下系统的次级通路鲁棒性非常恶劣。由图16（a）可见，此时如果不使用泄露算法，系统必然发散。如果引入一个β1=0.1的泄露算法，则系统能够非常轻易地收敛。由此验证了泄露算法对于提升次级通路鲁棒性的重要作用。

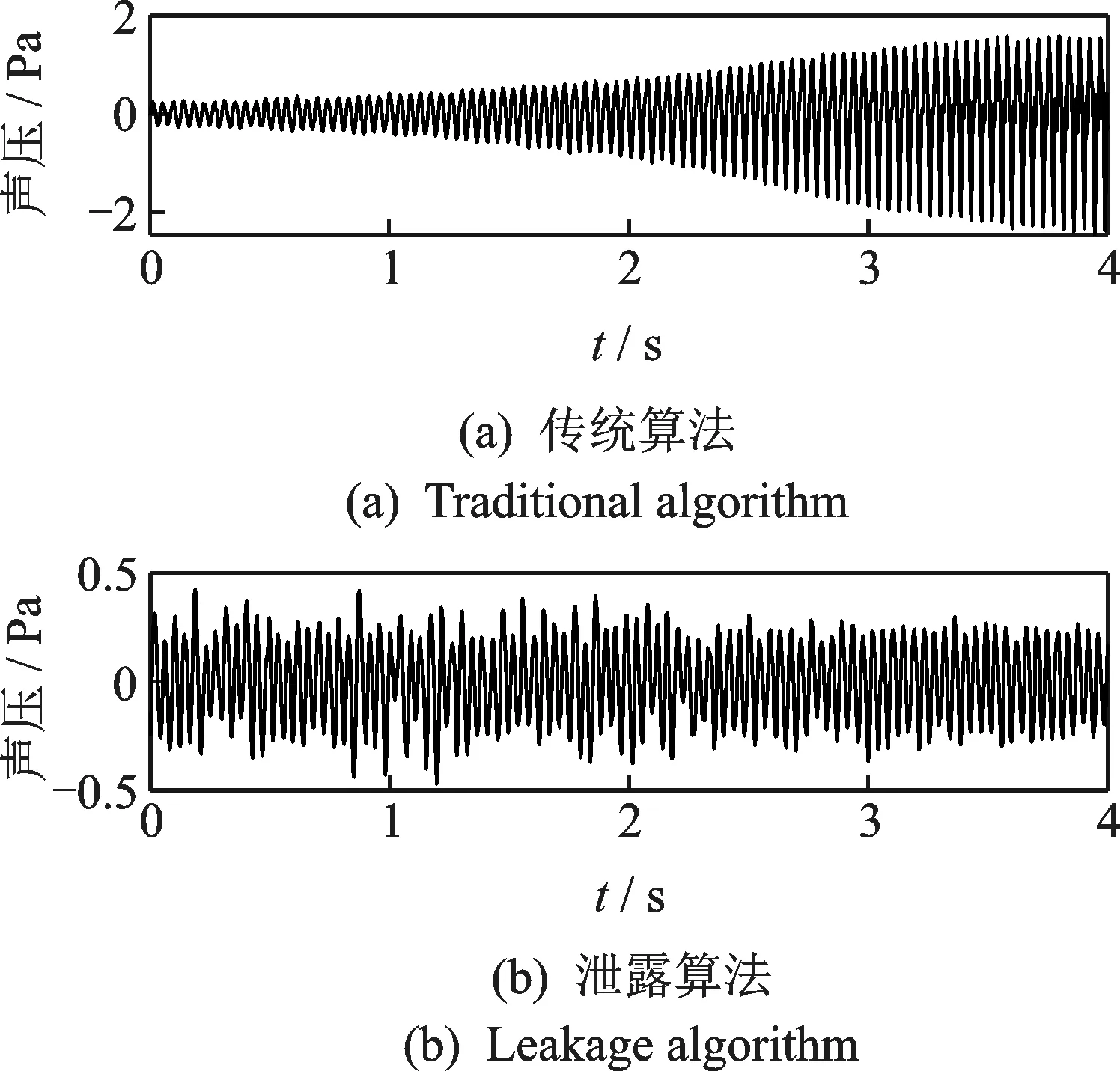
图16 泄露算法试验验证Fig.16 Leakage algorithm test verification

4 结束语

建立了多通道自适应陷波车内噪声主动控制系统的离散状态空间模型，提出评价系统降噪性能的收敛率和稳态误差增益两个指标。通过理论推导、数值仿真和实车试验的方法，分析了系统的次级通路鲁棒性问题，并推导了级通路完全失配的条件。分析表明，次级通路的改变对整个系统的稳态误差没有影响；对系统收敛性的影响有正有负，通过次级通路设计可以提升系统的收敛速度。结合分析结果对系统次级通路进行设计，通过改进次级通路，大幅提升系统的收敛速度。分析发现，次级通路反馈方法虽然可以提升系统鲁棒性，但是存在次级通路完全失配的风险。泄露算法虽然是以牺牲系统问题误差为代价来提升其鲁棒性，但是可以杜绝次级通路完全失配的分析。在实际应用中更具前景。