随机扰动项呈离散分布的库存路径和定价问题的模型与算法

杨华龙，辛禹辰，高浩然

(大连海事大学，交通运输工程学院，辽宁大连116026)

0 引言

供货商管理库存(Vendor Management Inventory,VMI)模式下，供货商需要进行IRPP优化决策。库存路径问题决策受客户需求影响，其目标是物流系统成本最小化；产品定价决策影响着客户需求，其目标是产品销售收入最大化。由此可见，库存路径问题和产品定价问题两者的决策要素相互制约、决策目标相左。尤其是在需求价格关系呈现随机扰动的情况下，IRPP优化决策愈加复杂，故需求价格函数随机扰动下的IRPP优化模型与算法研究具有重要的理论和现实价值。

Liu 等[1]分析了供货商库存路径决策与定价决策间的相互影响关系，研究表明，对库存路径问题和定价问题同时协调决策明显优于对两者的单独决策。考虑零售商位置差异对IRPP 的影响，Ahmadi-Javid 等[2]构建了包含零售商选址的IRPP模型，并设计分支定价算法求解。考虑智能互联网背景下实时信息对决策的影响，Sayarshad等[3]结合以供应链利润最大化为目标，建立了考虑零售商等待成本、库存持有成本和配送成本等分时段实时IRPP 模型。Dastaki 等[4]进一步针对跨区域的IRPP问题，基于分区定价策略，建立了二级(跨区域)IRPP非线性模型，并设计线性化近似求解方法。

现有IRPP 文献取得了许多有益成果，但均假定需求价格函数为确定型的线性关系，且零售商100%不缺货[5]。然而在实际场景中，除产品价格因素外，市场竞争强度、产品可替代性等许多其他因素也会对客户需求带来不确定影响。因而，需求价格函数具有随机扰动特征，且随机扰动项常常呈离散分布[6]，导致现实中即使产品价格给定，客户需求也会随机波动变化，造成零售商库存过剩或缺货，故考虑客户需求价格函数随机扰动的IRPP决策更符合实际。有鉴于此，本文利用需求价格函数中扰动项的离散分布率，依据供货商设定的库存服务水平，构建IRPP 期望值决策优化模型，以使IRPP 决策符合实际需要。

1 问题描述

考虑由一个供货商、多个零售商组成VMI 模式下的物流系统，当供货商对产品进行定价时，客户需求受到市场竞争强度及产品可替代性等因素的影响，需求价格函数含有随机扰动项。为满足客户需求，供货商还需要进行产品库存和配送路径决策。当配送量大于需求量时，造成产品过剩损失；当配送量小于需求量时，造成缺货损失。因此，需求价格函数随机扰动下IRPP 优化决策的实质是，通过分析客户需求价格函数关系，刻画其中随机扰动项的概率分布规律，以供货商期望收益最大化为目标，构建IRPP 优化模型，确定最优的产品价格、库存量、配送量和车辆路径。为便于问题建模，本文作如下假设：

(1)配送车辆是同质的；

(2)决策期内每个零售商只配送1次；

(3)配送车辆的起点与终点都是供货商配送中心。

2 模型构建

2.1 符号及变量

(1)集合和参数

Δ——配送网络节点集合，Δ={0,1,…,N}，0为供货商，N为零售商数量；

Ω——配送车辆集合，Ω={1,2,…,V}，V为配送车辆数量；

F——配送车辆固定成本；

C——配送车辆的单位距离行驶成本；

Lij——节点i到节点j的距离；

Q——车辆的最大载货量；

Gi——零售商i处单位产品的缺货损失成本；

Hi——零售商i处单位产品的过剩损失成本；

Ai——零售商i对产品的潜在需求量；

Bi——零售商i对产品需求函数斜率的绝对值；

U——供货商单位产品进货或生产成本；

α——供货商设定的零售商库存服务水平。

(2)决策变量

pi——供货商在零售商i的产品定价；

yvij——车辆v从节点i到节点j载运的产品数量；

xvij——0-1变量，若车辆v从节点i到节点j为1，否则为0；

qi——供货商给零售商i的产品配送量；

di——零售商i的产品需求量。

2.2 需求价格函数扰动项分析

根据问题描述，将客户需求与供货商产品定价关系[7]设为

式中：εi为零售商i(i∈{1,2,…,N})需求价格函数的随机扰动项，且εi呈离散分布，其分布形式可由具体的离散分布率表示。分布率可通过市场统计法或专家调查法获得。若随机扰动项εi第m个离散取值εim(εim按由小到大排序，m∈{1,2,…,M} ，M为εi离散取值的数目)的分布率为θim，则供货商在零售商i产品需求的第m个离散取值dim为

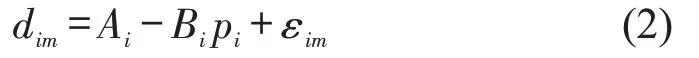
于是，在供货商设定的零售商库存服务水平α下，供货商配送给零售商i的产品数量应大于等于第m*(m*∈{1,2,…,M})个离散取值，即qi≥dim*，其中m*满足

综上所述,循证护理干预可以明显降低胸椎骨折患者术后并发症的发生率,改善患者疼痛程度和不良心理状态,有利于疾病康复。

由式(3)可知，无论随机扰动项εi的分布率θim(m∈{1,2,…,M})取值怎样变化，在设定服务水平α下，总能求得满足式(3)的m*，从而得到其对应的需求取值dim*。

供货商在零售商i产品过剩的数量为[qi-(Ai-Bi pi+εi)]+，供货商在零售商i产品缺货的数量为[(Ai-Bi pi+εi)-qi]+。这里[·]+为非负算子，供货商在零售商i的期望产品过剩损失成本Ei为

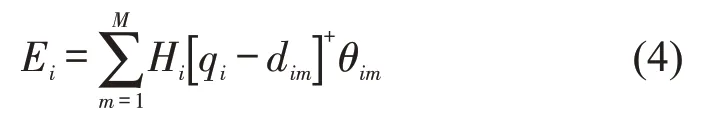
供货商在零售商i的期望产品缺货成本Fi为

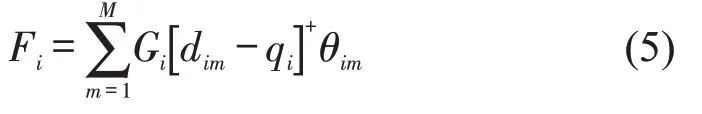
2.3 模型构建

根据上述需求价格函数扰动项分析，建立IRPP模型。

(1)目标函数

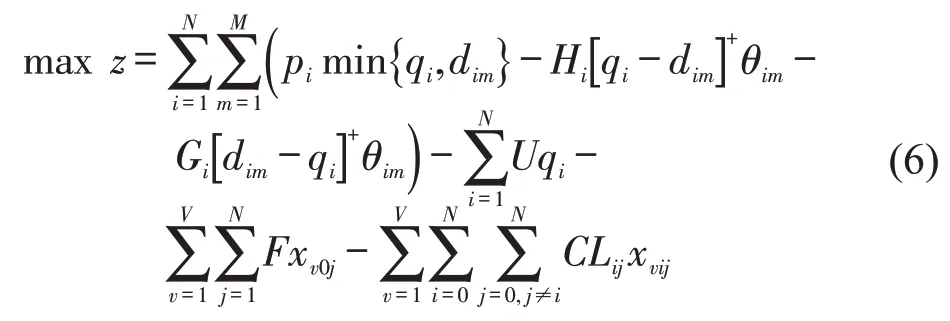
式(6)表示供货商期望收益最大化，第1项为期望收入，第2项为供货商配送产品的进货或生产成本，第3项为配送车辆的固定使用成本，第4项为配送车辆的行驶成本。

(2)约束条件

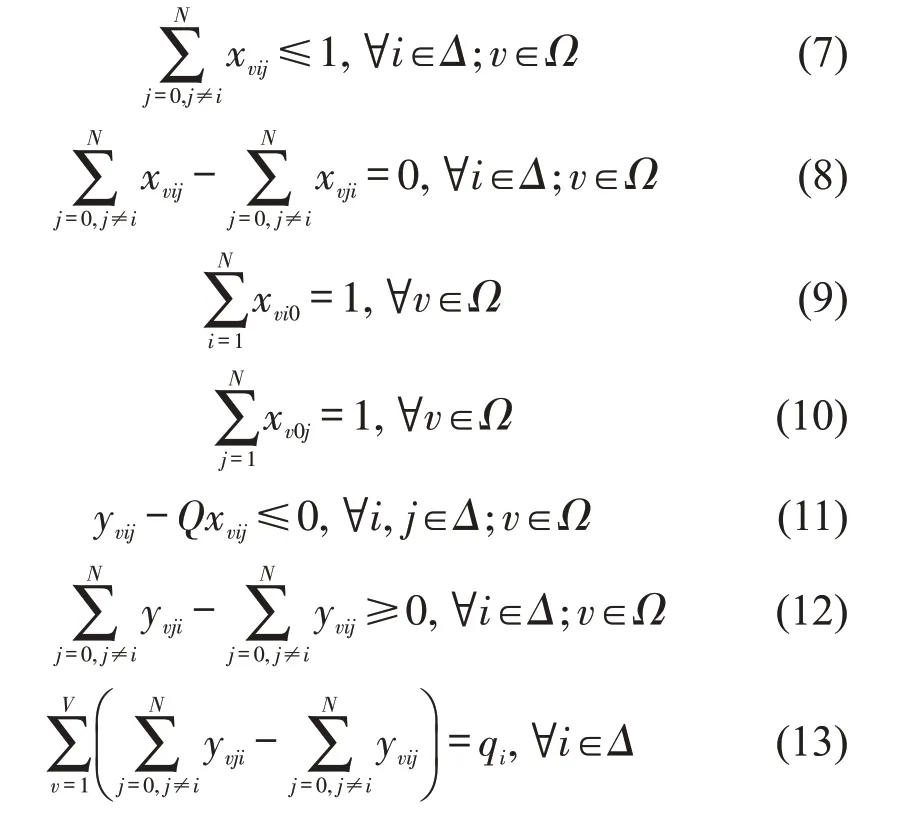
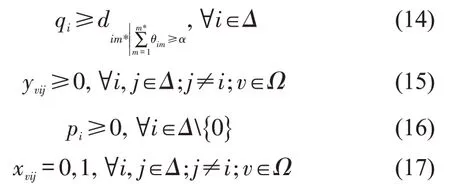
式(7)和式(8)表示车辆最多进出某节点一次，式(9)和式(10)表示配送车辆的起讫点都是供货商配送中心，式(11)为配送车辆的载运容量限制，式(12)和式(13)表示配送车辆在某一节点的配送量，式(14)表示配送量满足零售商库存服务水平要求，式(15)和式(16)表示变量的非负约束，式(17)表示0-1变量。

3 算法设计

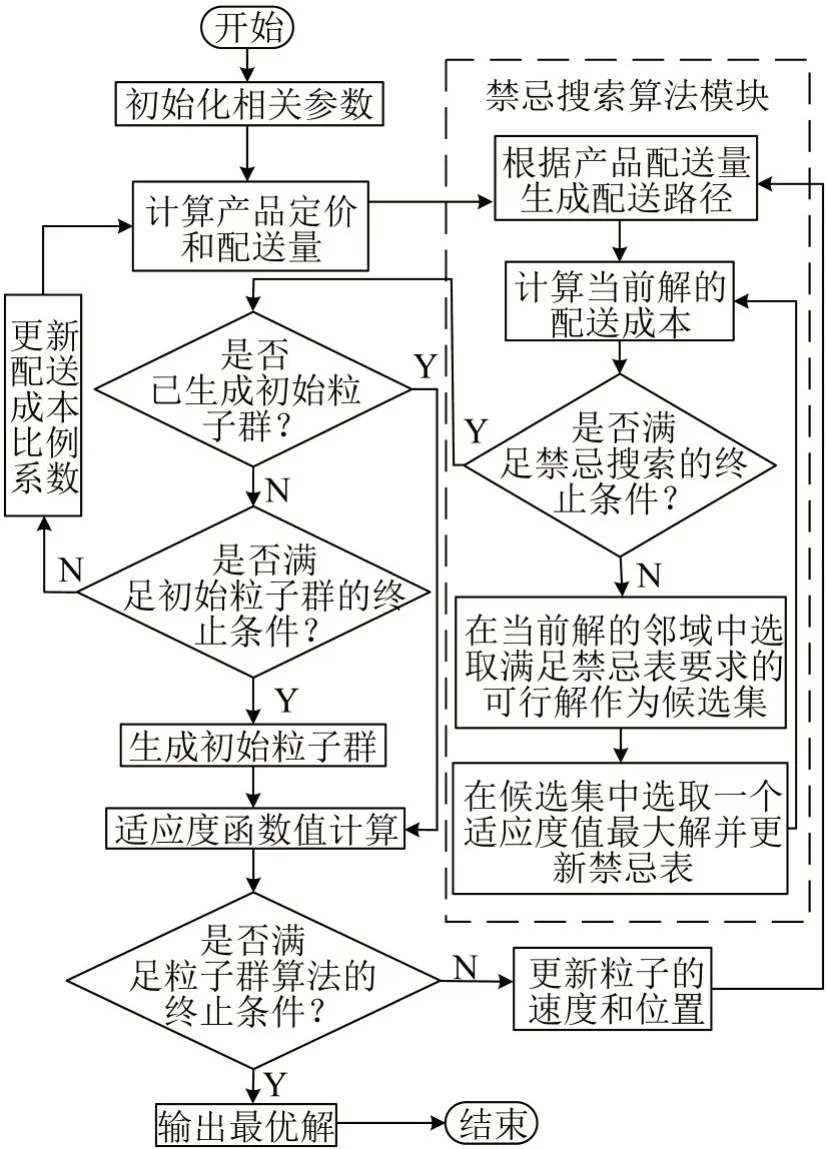
图1 算法设计流程Fig.1 Algorithm design process

3.1 初始化粒子群

本文按εim由小到大排序，当供货商对零售商i的产品定价为pi时，为保证一定的库存服务水平，供货商期望收益函数最大值必定在配送量qi≥dim*时取得。假定零售商i的产品配送成本与配送量成正比(比例系数γi0根据以往数值或经验预估获得)，则供货商在零售商i处的期望收益函数为

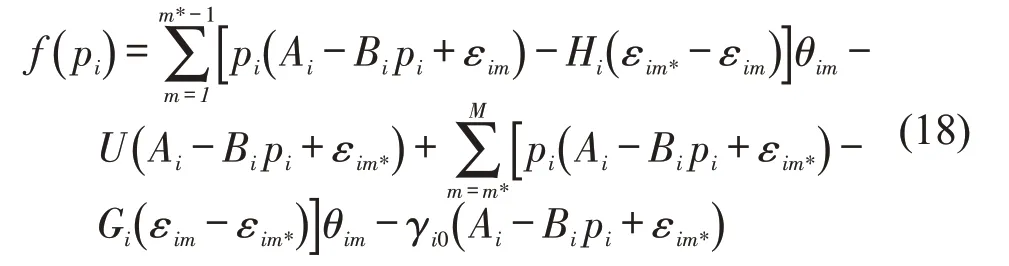
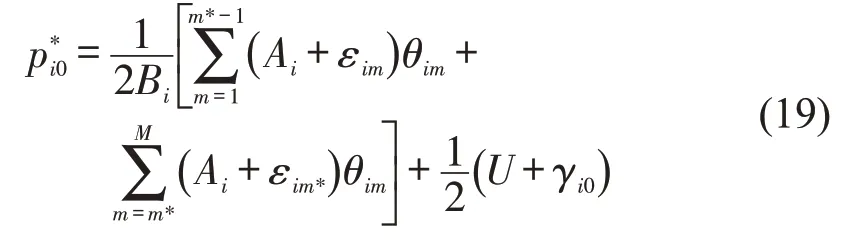
进一步可得供货商对零售商i的产品配送量初始优化解q*i0为

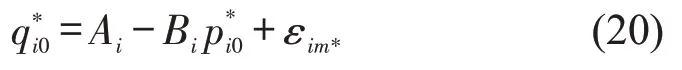
在此基础上，生成初始粒子群，具体步骤如下：

Step 1 根据配送量，采用禁忌搜索算法求出配送路径的初始优化解x*vij和y*vij。

Step 2 车辆v从节点i-1到达零售商i的行驶成本由零售商i承担，车辆v的固定使用成本和返回供货商配送中心路径的行驶成本由车辆v配送的所有零售商均担[1]，即当前优化解所对应的各零售商i的配送成本Ci为

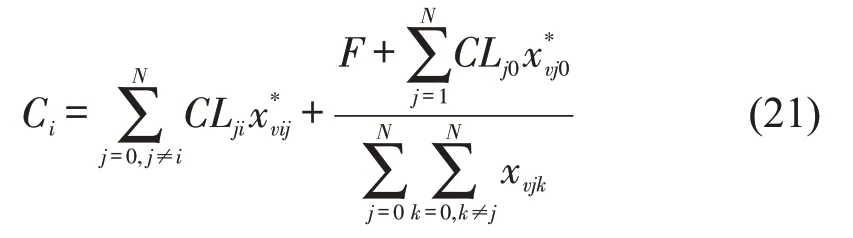
Step 3 计算各零售商i配送成本与配送量的比值γi。

Step 4 用γi替换式(19)中的γi0，计算得到新的产品定价p*i，并用p*i替换式(20)中的p*i0，计算得到新的产品配送量q*i。

Step 5 若不满足生成初始粒子群的终止条件(未达到最大循环次数)，返回Step1；否则，输出初始粒子群及其适应度值(即模型目标函数值)。

3.2 改进粒子群算法

设在一个D维搜索空间中，由K个粒子组成种群，在第t代第i个粒子位置表示为Xi,t=(xi1,xi2,…,xiD)，速度为Vi,t=(vi1,vi2,…,viD)，粒子在第t代个体的最优值为st，种群的最优值为gt，粒子在t+1 代速度Vid,t+1和位置Xid,t+1的更新公式分别为

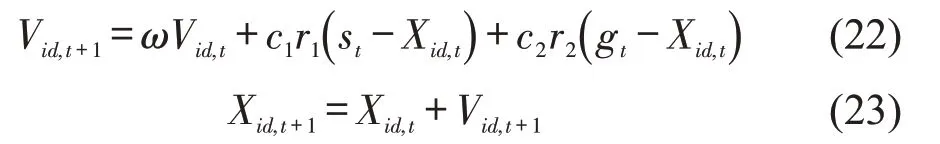
式中：c1、c2为加速因子；ω为惯性权重；r1、r2为介于[0,1]之间的随机数。加速因子c1，c2代表将粒子推向st和gt位置的加速权重。

本文对粒子群算法做以下改进：

(1)采用动态加速因子代替原有的常数加速因子，即

式中：cmax、cmin分别为加速因子最大、最小值；tmax为最大迭代次数。以此增加粒子空间搜索能力。

(2)采用线性递减的惯性权重代替原有的常数惯性权重，即

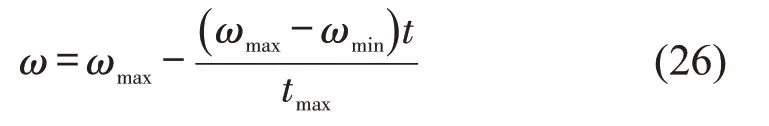
式中：ωmax、ωmin分别为惯性权重的最大、最小值。以此避免算法较早陷入局部极值。

改进的粒子群算法求解步骤如下：

Step 1 根据3.1节获取初始化粒子群和其适应度值，寻找并获得个体最优值st和群体最优值gt。

Step 2 更新粒子。首先，根据式(22)和式(23)对粒子进行速度和位置更新，获得各零售商产品定价和配送量；然后，运用禁忌搜索算法计算路径及各零售商配送成本；最后，按照式(6)计算粒子的适应度值。

Step 3 根据新种群中粒子适应度值更新个体最优值st和群体最优值gt。

Step 4 终止条件判断，判断粒子群算法迭代次数t是否达到粒子群算法的最大迭代次数tmax，如果未达到返回Step 2；否则，终止算法并输出最优值。

4 算例分析

4.1 数据选取及计算

在一个VMI 模式的生鲜品物流系统中，一家供货商为多家零售商配送某种产品，车辆最大载货量为4000 kg，车辆固定使用成本为300 元·辆-1，库存过剩成本损失为1元·kg-1，供货商的缺货损失成本为2元·kg-1，供货商设定的零售商库存服务水平为90%。供货商产品生产成本为0.5 元·kg-1，产品需求价格函数系数以及供货商和零售商的位置数据取自文献[1]，随机扰动项εi的离散分布率如表1所示。

表1 随机扰动项分布率Table 1 Random disturbance item distribution rate

设粒子种群规模为30，惯性权重最大、最小值分别为0.9、0.4，加速因子最大、最小值分别为2.5、0.5，最大迭代次数为200 次；设禁忌搜索算法迭代次数为50次，禁忌表长度为3，候选解集个数为5。

选取3组算例，分别包含8家(算例1)、15家(算例2)和25家(算例3)零售商，运用本文模型(分别采用本文设计的改进粒子群、传统粒子群和文献[1]中的禁忌搜索算法)与文献[1]模型进行计算结果对比。在处理器为Inter Xeon E5-2678(16核)，内存为32 GB的电脑上，利用python编程得到算例结果如表2所示。

表2 不同算法计算结果Table 2 Computing results with different methods

由表2可知，在满足相同服务水平下，采用本文模型方法得到的3 组算例供货商期望收益均优于文献[1]。结果显示，考虑随机扰动项，算例1、算例2和算例3中供货商期望收益分别提高了3.1%、3.5%和3.8%。此外，在本文模型下，改进粒子群算法得到的3组算例解质量(期望收益)和运算时间均优于传统粒子群算法和禁忌搜索算法。结果表明了本文模型及算法的适用性。

依据算例2，得到上述3种算法迭代收敛对比，如图2所示。

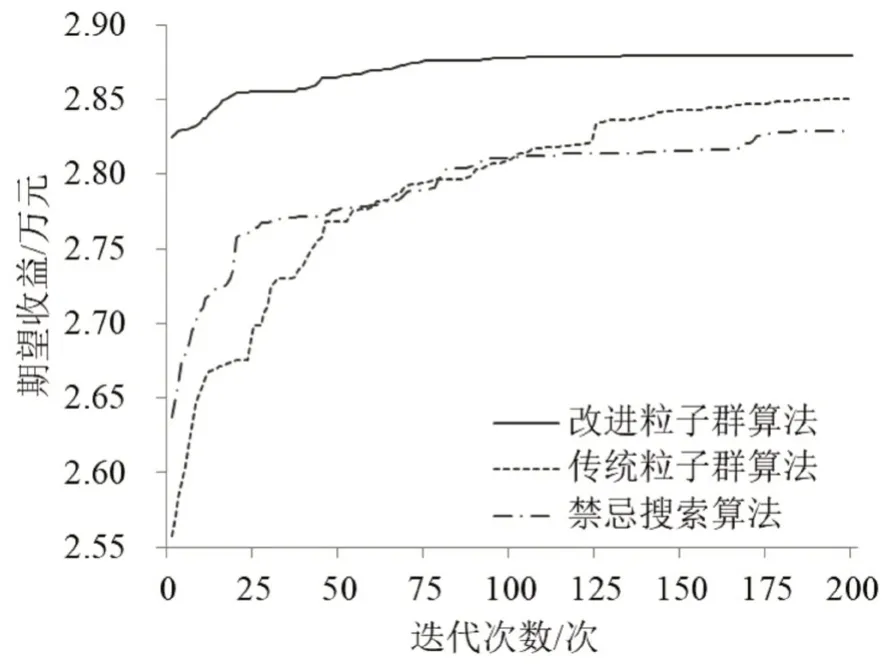
图2 算法迭代收敛对比Fig.2 Comparison of algorithms iteration convergence

由图2可知，相比于其他两种算法，本文算法能更快跳出局部最优解，进一步表明本文算法的有效性。

算例2中，供货商对各零售商的产品定价对比如图3所示，配送量对比如图4所示。

图3 各零售商产品定价对比Fig.3 Comparison of product pricing of retailers

从图3可以看出，考虑随机扰动项时供货商产品定价略高于不考虑时的定价；从图4可以看出，考虑随机扰动项时供货商配送量均高于不考虑时的配送量。这主要是因为考虑随机扰动项时，为满足客户服务水平要求，供货商需要配送更多的产品以降低缺货损失成本。当产品配送量增加时，根据需求价格函数关系，产品定价也会略有上涨。这表明考虑随机扰动项，产品定价和配送量均有所提高，供货商期望收益也因此增高。

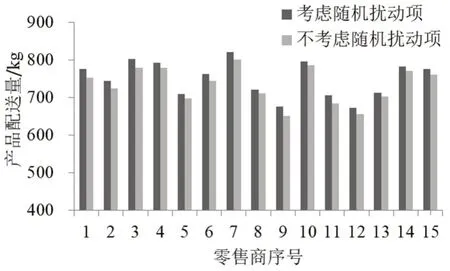
图4 各零售商产品配送量对比Fig.4 Comparison of distribution volume of retailers

4.2 灵敏度分析

随机扰动项εi的标准差反映了市场竞争强度和产品可替代性等对需求波动的影响程度，需求价格函数系数Bi反映了产品的需求价格弹性。依据算例2对其进行敏感性分析，结果如图5所示。

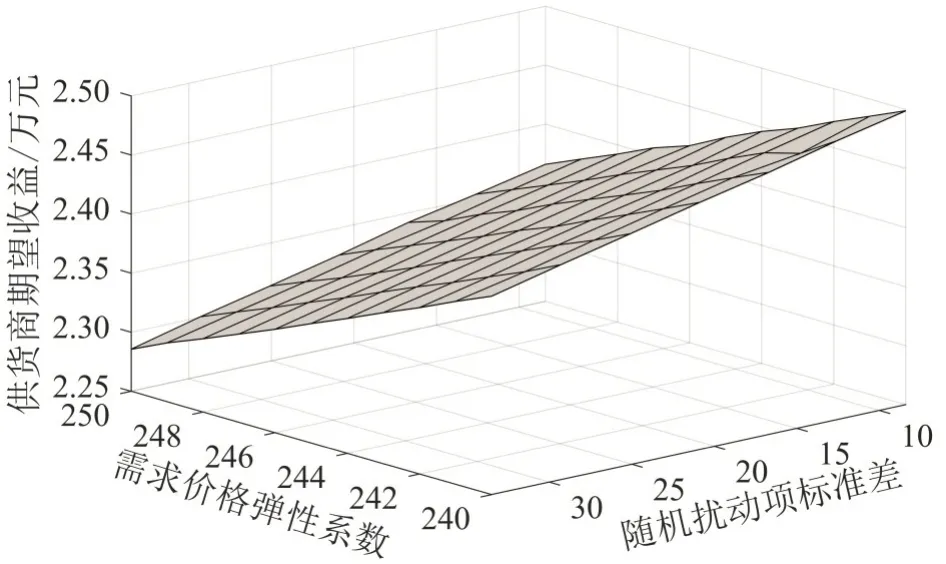
图5 供货商期望收益Fig.5 Expected revenue of supplier

由图5可知，εi标准差不断增大时，供货商期望收益呈近似线性减小，这主要是因为，在其他参数保持不变的条件下，客户需求di与其随机扰动项εi的标准差相等，即σi,d=σi(σi,d为di标准差，σi为εi标准差)。表1中εi的离散分布率与正态分布密度函数近似，故在给定库存水平α时，供货商给零售商i配送量便近似等于需求服从正态分布时的配送量，即qi≈μi,d+zασi,d，(μi,d为需求均值，zα为安全系数)。由此可见，qi与σi(=σi,d)呈近似线性关系，故随着σi的增大，配送量qi随之近似线性增大，产品的配送成本和过剩损失成本也近似线性增加，供货商的期望收益近似线性减少。同时，由图5可知，随着Bi的不断减小，供货商的期望收益呈线性逐渐增大，这主要是因为Bi值是需求价格函数的线性系数，Bi越小，说明客户对产品价格越不敏感，因而当供货商提高产品价格时，客户产品需求线性降低并不明显，使得供货商的期望收益呈线性增大。

5 结论

本文探讨了需求价格函数随机扰动项呈离散分布的IRPP优化问题，研究结果表明：在同样的库存水平要求下，相比于不考虑而言，考虑需求价格函数随机扰动因素，供货商期望收益将会得到有效提高；市场竞争强度和产品可替代性等因素对客户需求的影响越大，即需求价格函数随机扰动项的标准差越大，供货商的期望收益越小；产品需求价格弹性系数越小，即客户对产品价格的敏感性越小，供货商的期望收益越大。