智能网联车环境下交叉口车流轨迹优化模型

高志波，吴志周*，郝威，杨玥，龙科军，邹清全

(1.同济大学，道路与交通工程教育部重点实验室，上海201804；2.长沙理工大学，智能道路与车路协同湖南省重点实验室，长沙410004；3.上海汽车集团股份有限公司，上海201804)

0 引言

智能网联车环境下，不仅可以实时获取车辆及周围环境信息，还可以对车辆进行精确控制。因此，交叉口的控制对象将直接面向车辆，通过协调与合作，每一辆车将拥有唯一的通行方案，而无需信号灯控制[1]。如何设计高效的面向智能网联车通行的交叉口管控模型，已成为近年来的研究热点之一[2-3]。

国内外学者对智能网联车环境下的交叉口管理进行了较多研究，集中在车辆到达时序优化和车辆轨迹优化等方面。在车辆到达时序优化方面，Dresner 等[4-5]基于排队论建立了先到先服务(First Come First Served,FCFS)的交叉口控制模型，并证明该模型相对于信号控制策略，可以显著降低车辆延误。然而，在过饱和、车辆编队行驶等情况下，FCFS模型的延误会比信号控制更大[6]。姚志洪[7]等引入优化时间区间的概念，建立了基于混合整数规划的冲突区时序优化模型。吴伟等[8-9]将交叉口空间离散化，提出面向自由转向车道的交叉口控制模型；但模型中车辆进入交叉口的速度固定且相等，限制了其适应性。在车辆轨迹优化方面，Ma等[10-11]设计了一种反向射击式车辆轨迹优化算法，并研究了算法的计算复杂度和移动性，随后又将其应用于交叉口和瓶颈区控制。罗孝羚等[12]提出了一种两阶段优化模型，第1阶段是优化车辆进入时序，第2阶段是优化车辆轨迹。然而，模型中车辆到达时序和车辆轨迹分开优化，使其无法获得全局最优解。此外，也有部分学者使用博弈论[13]、多智能体学习[14]等理论对智能网联驾驶下的交叉口控制进行建模。

综上所述，已有研究要么仅考虑车辆到达时序的优化，要么将车辆到达时序和车辆轨迹分别优化，导致其无法获得最优解。本文基于上述思路，以所有车辆在控制区域的行程时间与油耗加权最小为目标，建立车辆到达时序和速度协同优化的交叉口控制模型，促进车辆通行效率和能耗的均衡，提高交叉口整体效益。

1 问题描述

在智能网联车环境下，交叉口将无需信号灯控制，且每一条进口车道均能“左直右”通行。如图1所示，车辆可以借助“自由转向车道”实现出口车道的选择(轨迹①)，也可以在路段上提前换道实现进口车道的选择(轨迹②)。本文将车辆轨迹分为控制区域和冲突区域两部分，在控制区域进行车辆速度优化和换道决策，在冲突区域进行车辆到达时序优化和路径选择。因此，本文研究问题可以描述为：在一定的规划时间内，如何合理优化车流轨迹，使所有车辆通过交叉口的时间最短，油耗最低。

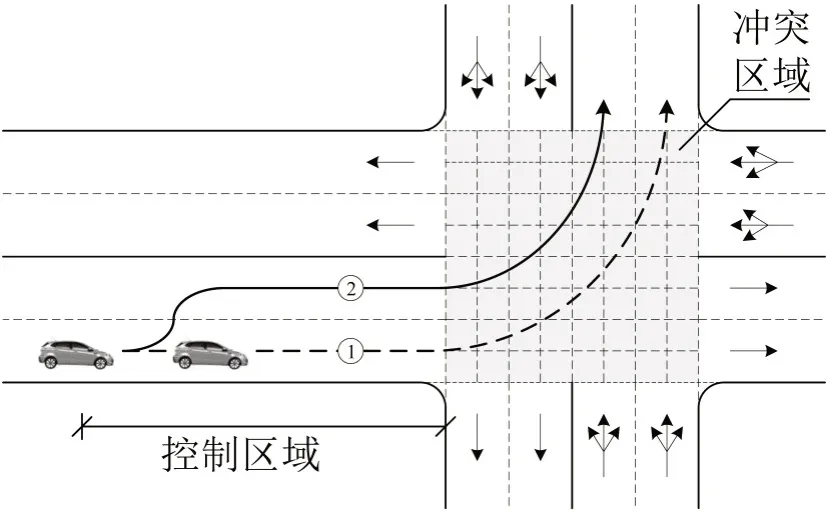
图1 交叉口研究区域示意Fig.1 Study area layout of intersection

2 模型构建

2.1 模型假设

(1)车辆在冲突区域内匀速行驶，且不能停车；

(2)假设通信和车辆控制均能满足自动驾驶需要，不考虑时延；

(3)车辆驶离控制区域、到达停车线和驶入冲突区域为同一状态；

(4)头车不参与换道，仅考虑跟随车的换道行为，且只在相邻车道最多换道1次；

(5)车辆仅在滚动优化时间点进行换道条件判断和决策，且换道是瞬时完成的。

2.2 车辆到达时序优化模型

(1)车辆到达网格时刻约束

将交叉口冲突区域离散化处理，参考文献[8]建立的车辆轨迹方程和交叉口内部空间映射关系，车辆进出网格的时刻为

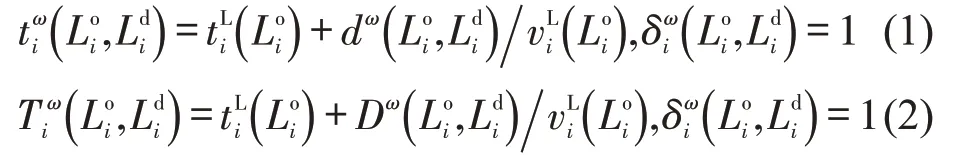
式中：Loi为车辆i进口选择车道；Ldi为车辆i出口选择车道；tiω(Loi,Ldi)为车辆i经路径(Loi,Ldi)驶入网格ω的时刻；Tiω(Lio,Ldi)为车辆i经路径(Loi,Ldi)驶离网格ω的时刻；tLi(Loi)为车辆i到达停车线的时刻；dω(Loi,Ldi)为车辆i经路径(Loi,Ldi)从停车线至车头驶入网格ω的轨迹长度；Dω(Lio,Ldi)为车辆i经路径(Loi,Ldi)从停车线至车尾驶出网格ω的轨迹长度；为车辆i到达停车线的速度；δiω(Loi,Ldi)为0-1变量，等于1 时表示车辆i经路径(Loi,Ldi)经过网格ω，否则不经过。

为确保安全，同一时刻同一网格只能被1辆车占用，即

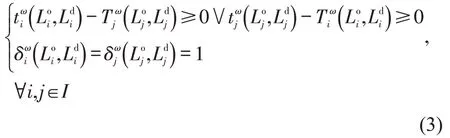
式中：j为车辆j的编号；I为所有车辆集合。

(2)换道约束

由于头车不考虑换道，仅需考虑出口道选择，可以表示为

式中：为头车集合；Lci为车辆i当前时刻所在车道。

对于跟随车，需要在满足换道条件后才能实现对进口车道的优化。由于车辆仅在滚动优化时间点进行换道决策，是否满足换道条件可参考文献[15]判断。当满足换道条件时，换道决策表示为

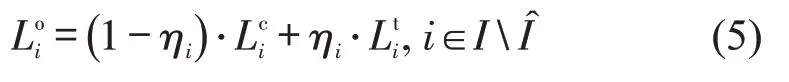
式中：Lti为车辆i的目标车道；ηi为0-1变量，等于1时表示换道，否则不换道。

(3)车辆到达时刻约束

当车辆加速至最大限制速度时，并以最大速度巡航，如图2(a)所示，此时到达停车线时间最短，即

式中：vmax为最大限制速度；a+为最大加速度；t(i

0)为初始时刻，这里t(i0)=0；v(i0)为初始时刻车辆i的速度；di为初始时刻车辆i到停车线的距离；vr为车辆到达停车线的临界速度；Δt(i1)为加速至最大限制速度所需时间；Δt(i2)为以最大速度巡航至停车线所需时间；tmiin为车辆到达停车线所需最短时间。

当车辆减速至最小限制速度时，并以最小速度巡航，如图2(b)所示，此时到达停车线时间最长，即

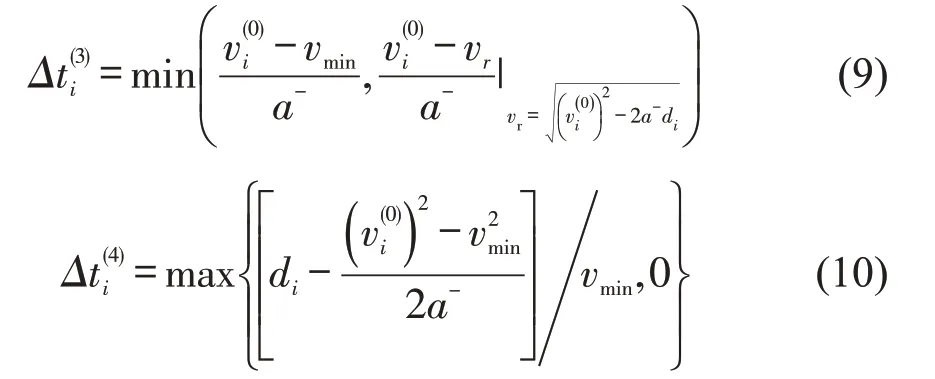
式中：vmin为最小限制速度；a-为最大减速度；Δt(i3)为减速至最小限制速度所需时间；Δt(i4)为以最小速度巡航至停车线所需时间；为车辆到达停车线所需最长时间。

因此，车辆到达停车线的时刻满足

(4)目标函数

车辆到达时序优化中，目标是规划时间段内所有车辆在控制区域的行程时间最短，考虑到该目标会迫使车辆违反意愿而接近限速的情况，将车辆期望到达时刻与实际到达时刻的偏差加入到目标函数中，即

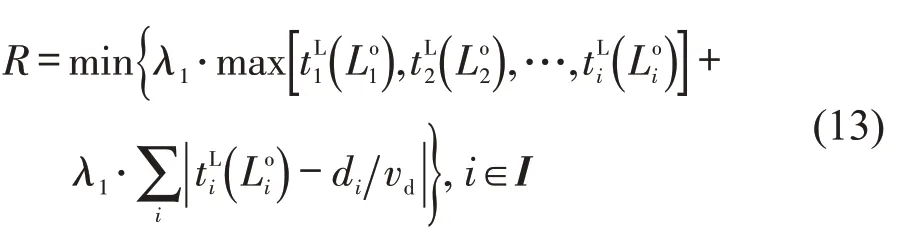
式中：λ1和λ2为偏差系数；vd为车辆期望速度。

2.3 车辆速度优化模型

车辆到达停车线的时刻由车辆到达时序优化模型得到后，在控制区域的车辆速度优化可看作一个终端时间和位置已知的最优控制问题。

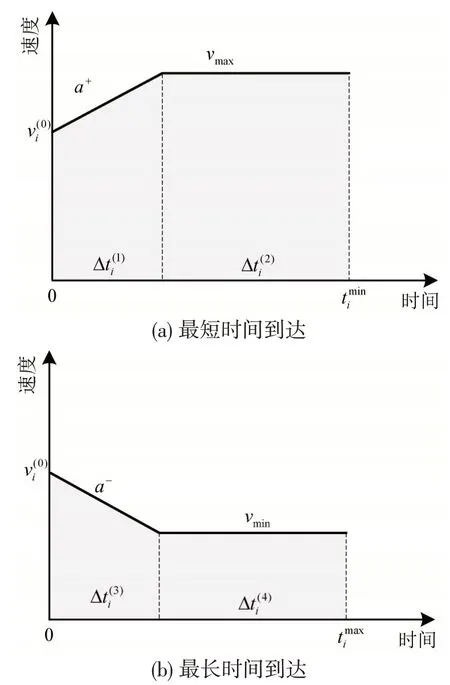
图2 车辆到达极限情况Fig.2 Limit condition of vehicle arrival

(1)状态描述

定义状态变量xi(t)=[xi(t),vi(t)]T，其中，xi(t)、vi(t)分别为车辆i在时刻t的位移和速度，控制变量为车辆期望加速度ui(t)，则状态方程表示为

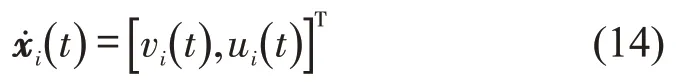
(2)成本函数

车辆速度优化中，目标是车辆的总油耗最低，参考文献[16]，成本函数可以表达为

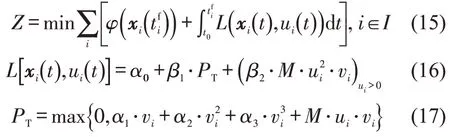
式中：tfi为终端时刻；φ(xi(tfi))和L(xi(t),ui(t))分别为终端成本和运行成本；PT为总牵引力。根据文献[17]，各参数取值为：α0=0.666mL·s-1，β1=0.0717mL·kJ-1，β2=0.0334mL·(kJ·m·s-2)-1，α1=0.269kN，α2=0.0171 kN·(m·s-1)-1，α3=0.000672 kN·(m·s-1)-2，M=1860 kg。

(3)约束条件

初始状态约束

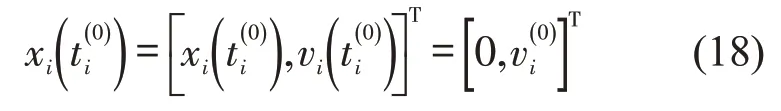
终端位置和时刻约束

考虑车辆性能，车辆的加速度和速度需满足边界约束，即

此外，车辆还需与前车保持一定安全间距，即

式中：τi、σi分别为车辆i与前车i-1 的时间偏移和空间偏移，设置τi=0.4 s，σi=2.0 m。

2.4 车流轨迹优化模型

由分析可知，本文建立的交叉口控制模型既要使所有车辆行程时间最短，还要使油耗最低。为实现两个目标的集成优化，建立目标函数为

式中：k1和k2为目标权重系数。

约束条件为式(1)～式(12)，式(14)～式(22)。

3 求解框架

当车辆到达停车线的时刻确定时，车辆速度优化模型可通过求解最优控制问题输出车辆到达停车线的速度；当车辆到达停车线的速度确定时，车辆到达时序优化模型通过线性化转化为混合整数线性规划问题，求解输出车辆到达停车线的时刻。

3.1 线性化

式(3)为条件判断约束，引入0-1变量和较大正值将其转化为线性约束，即

式中：B1和B2为较大正值；ζωij为0-1变量，表示车辆进入网格ω的先后次序。

式(13)的目标函数中含有最大值和绝对值约束，引入辅助变量将其转化为

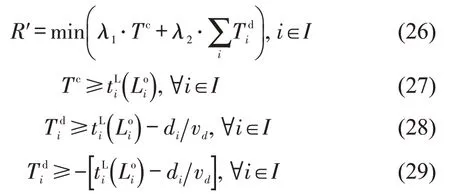
式中：Tc和Tid均为辅助变量。

3.2 求解步骤

基于模型特征，设计迭代式算法求解，步骤如下。

Step 1 参数初始化。输入车辆配置参数和初始状态信息，交叉口几何参数与辅助参数。设置作为车辆优化模型终端时刻的初始值，开始迭代计算。

Step 2 根据给定的终端时间tif，采用GPOPS(Gauss Pseudospectral Optimization Software)工具求解车辆速度优化模型，考虑到固定终端时刻存在无最优解的情况[17]，设置tfi=tfi+0.1s确保解的有效性和计算效率，输出车辆到达速度vLi和更新后的，进入Step 3。

Step 3 基于给定的车辆到达速度和终端时间tfi，将式(12)调整为，采用Gurobi 工具求解关于时序优化的混合整数线性规划问题；结果输出车辆到达时刻tLi，进入Step 4。

Step 4 计算车流轨迹优化模型目标值，并进入终止条件判断，前后两次迭代结果之差小于5%。当满足终止条件，算法终止；否则，令tfi=tLi，返回Step 2。

4 模型验证

4.1 实验设计

以一个最基本的交叉口为例，对模型的效益进行验证。该交叉口双向4车道，车道宽度为3 m，如图3所示。将交叉口冲突区域离散化处理，划分为若干个正方形网格，网格边长为3 m。选取某一时刻同时到达的16 辆车进行分析，其基本属性包括车辆进出口方向、车道、位置和速度，如表1所示。

图3 交叉口进口道及网格划分Fig.3 Entrance lane of intersection and grid partitioning

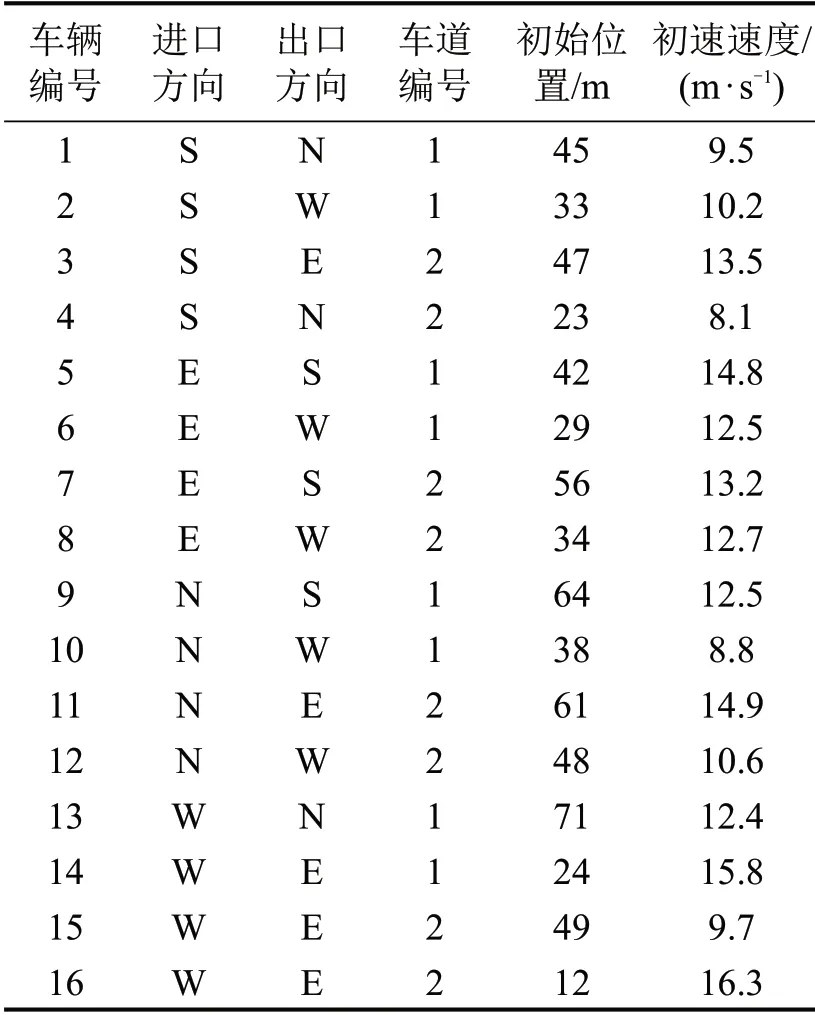
表1 到达车辆的基本属性Table 1 Attributes of arrival vehicles

4.2 模型结果与对比分析

考虑车辆动力性能、限速和燃油等情况，加速度取值区间设置为[-3,3]m·s-2，最小和最大限制速度分别为4.47 m·s-1、16.67 m·s-1，期望车速为13.89 m·s-1，车辆长度为4.5 m。根据文献[1]，偏差系数设置为：λ1=λ2=0.5。根据文献[10]，目标权重系数设置为：k1=5.6 s-1，k2=1.0 mL-1。选取MATLAB 作为编程环境，并调用GPOPS和Gurobi工具箱进行求解，输出车辆的最佳路径、时刻、到达速度与时刻、延误及油耗，如表2所示。由结果可知，车辆8、10和11进行了换道，车辆总延误为15.22 s，车均延误为0.95 s；总油耗为53.96 mL，车均油耗为3.37 mL。

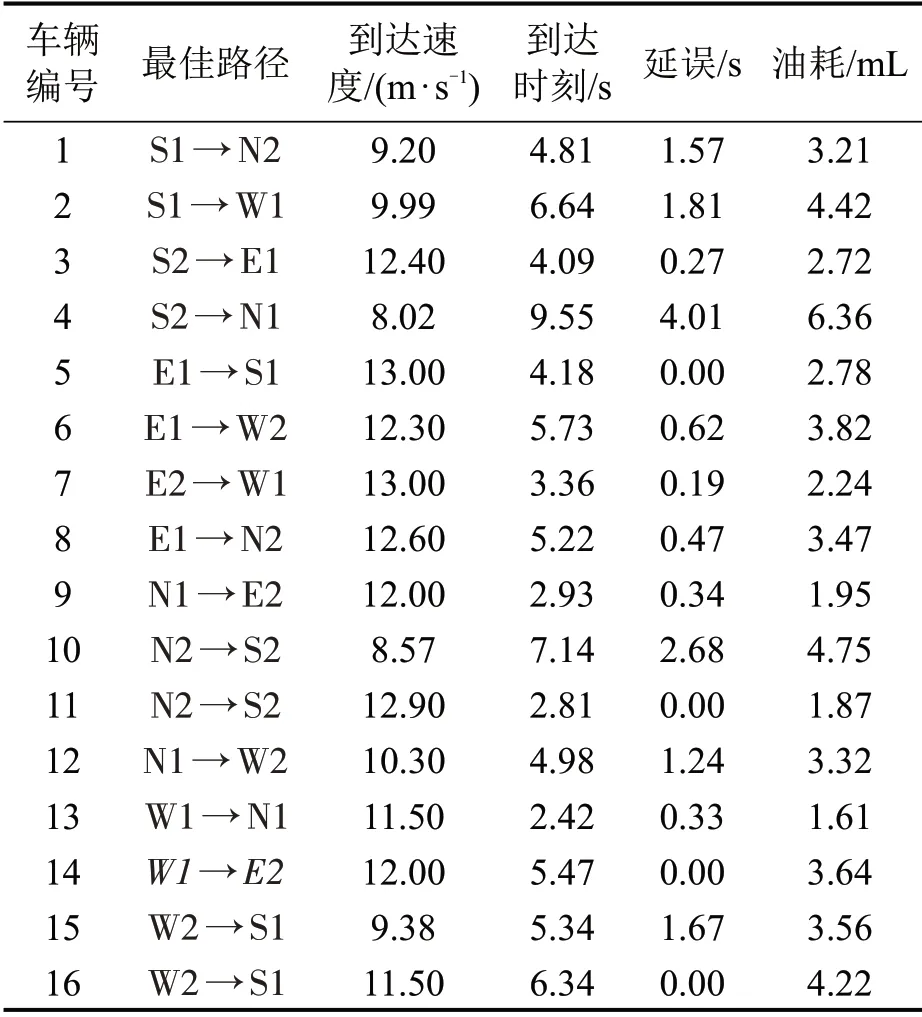
表2 本文模型计算结果Table 2 Results of proposed model

为进一步验证本文模型的先进性，与两阶段优化模型[12]进行对比分析。两阶段模型的车辆总延误为22.38 s，车均延误为1.40 s；总油耗为59.87 mL，车均油耗为3.74 mL。与两阶段模型相比，本文模型能降低车均延误32.1%；降低车均油耗9.9%。从图4(a)可以看出，本文模型和两阶段模型的最大延误车辆均为车辆4，延误分别为3.61 s 和4.01 s，相差不大；本文模型虽然增加了部分车辆的延误(车辆4、10 和12)，但通过协调优化，能显著降低车辆总延误。从图4(b)可以看出，本文模型中每辆车的油耗均小于两阶段模型，这也进一步说明，本文模型能很好地均衡时空资源，在降低车辆延误的同时节省油耗。

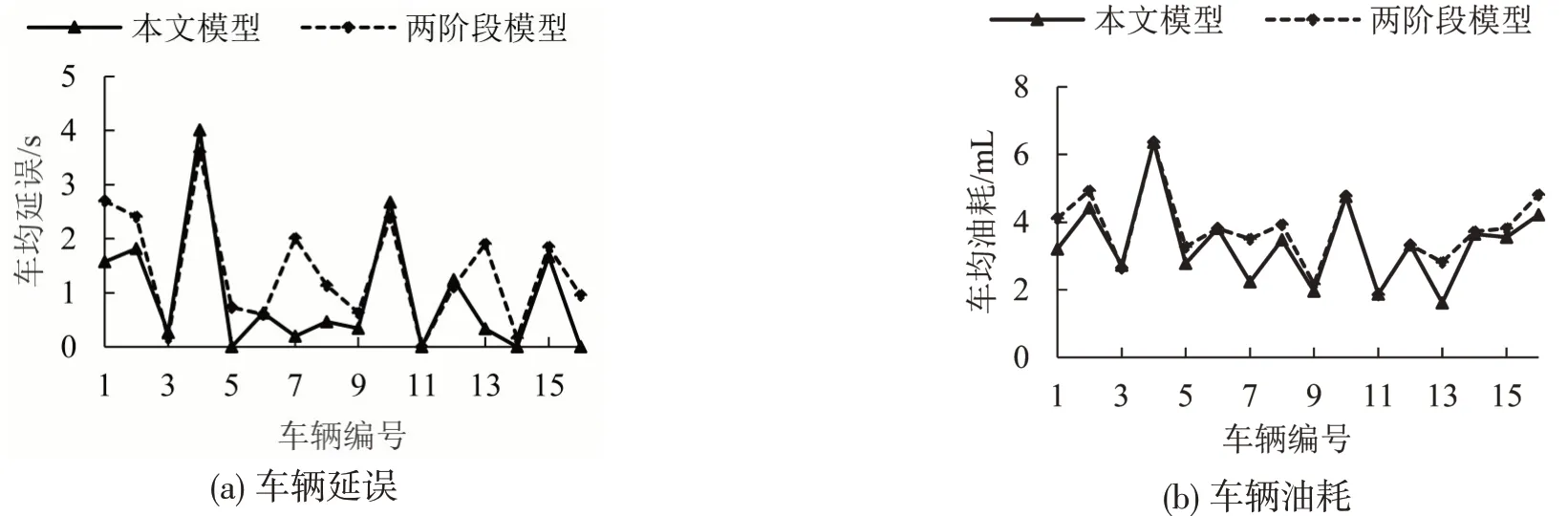
图4 车辆延误与油耗对比Fig.4 Comparisons of vehicle delay and fuel consumption

4.3 敏感性分析

(1)期望速度

固定其他参数不变，使期望速度在42～60 km·h-1之间变动。采用总行程时间和总油耗作为评价指标，输出结果如图5所示。当期望速度从42 km·h-1增加到60 km·h-1时，车辆总行程时间从86.55 s 降低到79.16 s，总油耗从57.64 mL 降低为52.72 mL，降低幅度均为8.54%。当期望速度较低时，车辆将以期望车速行驶，总行程时间和油耗减少明显。当期望车速靠近最大限制速度时，总行程时间和油耗量基本不变。这是因为，较大速度会导致车辆频繁加减速，从而增加油耗；而另一方面，速度增加将有助于车辆更快驶离交叉口，又可以减少油耗。

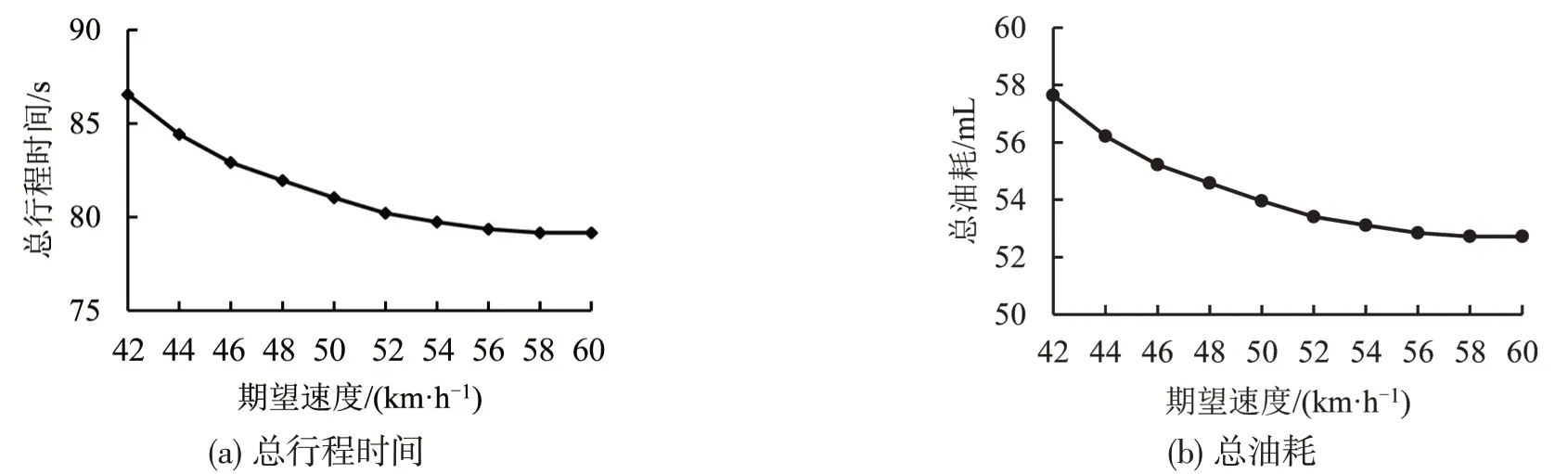
图5 期望速度敏感性分析Fig.5 Sensitivity analysis on desired speed

(2)最大加(减)速度

固定其他参数不变，使最大加(减)速度的绝对值在2.6～3.5 m·s-2间变动。车辆总行程时间和总油耗，如图6所示。当最大加(减)速度的绝对值增加时，车辆总行程时间和总耗油量基本不变。这也说明，本文模型能适应不同的最大加(减)速度要求，具有良好的适应性。

图6 最大加(减)速度敏感性分析Fig.6 Sensitivity analysis of maximum acceleration or deceleration

5 结论

本文建立了车辆到达时序和速度协同优化的交叉口控制模型，克服了在现有控制方式下，车辆到达时序和车辆轨迹分开优化而无法获得最优解的不足，提高交叉口的整体效益。在建立车辆到达时序优化模型和车辆速度优化模型的基础上，以所有车辆在控制区域的行程时间与油耗加权和最小为目标，使用迭代算法同时求解最佳车辆到达时刻与速度。实验结果表明，相比于车辆时序和轨迹分别优化的两阶段模型，本文模型能够降低车均延误32.1%，减少车均油耗9.9%。对速度、最大加(减)速度的敏感性分析进一步表明模型具有良好的适应性，能更好地分配时空资源，实现通行效率和能耗的均衡。