钻井机器人偏心流道冲蚀实验及数值模拟研究

肖晓华，代继樑，朱海燕，赵建国

1.西南石油大学网络与信息化中心，四川 成都 610500；2.西南石油大学机电工程学院，四川 成都 610500；3.油气藏地质及开发工程国家重点实验室·成都理工大学，四川 成都 610059

引言

连续油管水平井钻井技术具有很多优点，有望成为非常规油气资源钻井技术的替代方案。然而，目前连续油管钻井在水平井中容易发生管串屈曲“锁死”现象[1-2]，在一定程度上限制了其在水平井钻井领域的推广应用。通常的解决方案是使用水力振荡器或加入润滑剂[3-5]来提高连续油管水平井段的延伸能力，但该方式没有从根本上解决连续油管屈曲“锁死”的问题，使得微小井眼水平井连续油管钻井延伸能力仍然有限[6]。

为了提升微小井眼水平井连续油管钻井水平段延伸能力和自动化水平，提出了采用钻井机器人牵引连续油管钻井的方案[7-12（]图1）。该方案将钻井机器人置于连续油管与定向工具之间。通过钻井液驱动钻井机器人，利用机器人为钻具提供钻压的同时牵引连续油管前进；该方案改变了连续油管的受力状态，可明显减少连续油管屈曲“锁死”的现象。

钻井机器人动力学模型如图2 所示，该方案的特点是：钻井机器人能同时为连续油管和钻具提供牵引力和钻压。为此钻井液必须通过机器人内部流道，作用于活塞缸和动力钻具才能为整个系统提供动能。该方案对机器人的尺寸和牵引力要求极高，目前国内外对于微小井眼连续油管钻井机器人的研发仍处于概念设计或实验研究阶段，仅美国WWT公司加工了一套试验样机，该钻井机器人样机外径尺寸较大，最小外径为119.3 mm[13]，未达到微小井眼的尺寸要求。

图1 钻井机器人井下安装位置示意图Fig.1 Downhole installation position of drilling robot

图2 钻井机器人动力学模型图Fig.2 Dynamic model diagram of drilling robot

在有限的设计空间内，连续油管钻井机器人流道不仅要满足钻井液携岩要求的过流面积，还必须为连续油管钻井机器人预留其他零件的布置空间，这给连续油管钻井机器人流道的结构设计造成了极大的困难。所以，流道的设计是钻井机器人设计的重点之一。流道是影响钻井机器人性能和使用寿命的关键。而影响流道寿命的主要因素是泥浆中固体粒子的冲蚀，但目前尚未有普适的冲蚀理论模型预测流道寿命[14-15]，冲蚀模型在不同条件下仍需通过实验确定和校正参数。因此，研究在钻井泥浆条件下流道的冲蚀规律，设计满足工程需要的微小井眼钻井机器人的携岩流道具有重要意义。

1 钻井机器人携岩流道结构优化设计

1.1 基础参数及方案设计

微小井眼水平井连续油管钻井携岩排量基本在7∼10 L/s[16]，取极限流量10 L/s，根据钻井现场实际，其他基础参数见表1。

携岩流道结构设计的难点在于其位于钻井机器人内部，且为了保证与钻井机器人两端连接件流道相通，钻井机器人入口和出口流道两端必须居中，但在钻井机器人内部又必须考虑留出尽可能大的空间放置控制单元，为此，提出了5 种钻井机器人内部流道的结构设计方案，如图3 所示。

表1 流道设计理论参数表Tab.1 Flow channel design basic parameters

图3 微小井眼连续油管钻井机器人流道形状截面图Fig.3 Flow channel shape and section of coiled tubing drilling robot for micro hole

以上方案流道均需要两端居中布置，因此，除圆环形流道和圆形中置流道外，其他3 种流道的中间部分为靠机器人本体下方的水平流道，水平流道与两端流道通过倾斜流道连接。所以，本文设计的钻井机器人内部流道为三段式偏心结构。

由图3 可知，参照微小井眼尺寸，设定以钻井机器人外径为100 mm，壁厚5 mm，在相同的过流面积（当量直径为20 mm）下，弯月形偏心携岩流道所预留空间宽度，达到85.00 mm，环形流道约77.46 mm，椭圆形偏心携岩流道75.00 mm，偏心圆形流道65.00 mm，中置圆形流道可用宽度最小，仅为35.00 mm，因此，排除圆形中置流道方案。

流道的设计除考虑可用空间大小外，还需要考虑流道的流场特性，因此，下面将通过分析流道流场分布来进一步优选方案。

1.2 流道形状优选

携岩流道需要使含砂流体顺利流通，不能存在低速死区和过大压耗，同时流速分布对流道冲蚀也有较大影响，有必要对不同形状的流道进行流速分析。利用ANSYS 建立当量直径为20 mm 的不同形状流道模型，以泥浆为介质，不同形状流道泥浆流速分布云图如图4 所示。

从图4 中可以看出，不同形状流道的流速分布不同：圆形、圆环形、椭圆形流道的流速在边界处最小，从边界到流道中心逐渐增大，在中心处最大（图4a，图4b，图4d）；而弯月流道内侧最小，从内侧到外侧逐渐增加，在外侧流速最大（图4c），此种情况容易对流道造成冲蚀破坏，因此，弯月形流道不宜作为钻井机器人流道。

对当量直径相同，但形状不同的携岩流道进行稳态流体运动仿真，得出相同当量直径不同形状流道进出口压力，计算得不同流道的压力损耗梯度如表2 所示。

由表2 可以看出，圆形流道环压力损耗梯度最小，仅0.010 MPa/m，环形流道压力损耗梯度最大，达到0.031 MPa/m，比椭圆形流道高出158.3%，故环形流道压力损耗梯度太高会导致压耗过高不宜作为流道。虽然圆形和椭圆形流道压力损耗梯度较小，但椭圆流道目前加工困难，综合以上分析，圆形偏心携岩流道为目前最佳选择。

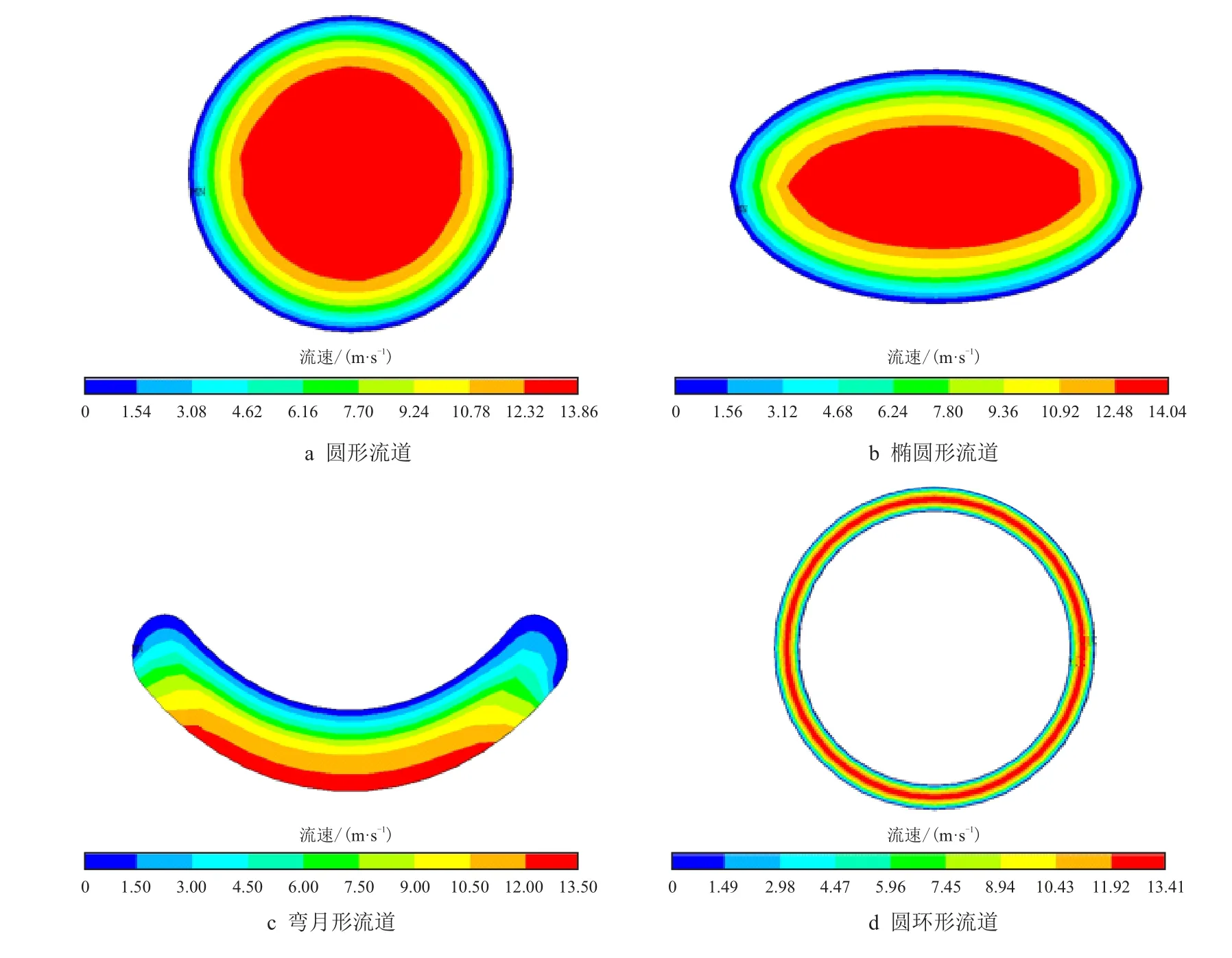
图4 不同形状流道泥浆流速分布云图Fig.4 Cloud chart of mud flow velocity distribution in channels of different shapes

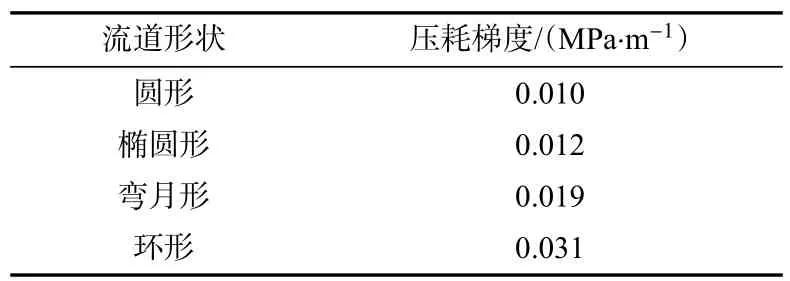
表2 不同形状流道的压耗对比Tab.2 Comparison of pressure and consumption in different flow channels

1.3 流道直径参数优选

因为流道直径对内部空间和压耗均有影响，故在确定了流道截面形状后，还需确定圆形偏心携岩流道的直径以及通过数值仿真验证整个流道寿命。

根据表1 的数据和图3 的流道设计参数，建立计算模型，计算出不同流道进出口压力值，得到压耗结果如图5 所示。

由图5 可知，流道压耗与直径成反比，随着钻井机器人流道的增大，压耗逐渐减小，当流道直径小于20 mm 时压耗增大明显，当流道直径大于20 mm时，压耗变化不大，考虑钻井机器人内部空间限制，选取20 mm 为流道内径较为合适。

图5 圆形流道直径对压耗的影响Fig.5 The relationship between circular channel diameter and pressure

圆形偏心携岩流道工作在高压、高速固液两相流动的工况下，需要考虑两相流体冲蚀。现有仿真模拟软件的冲蚀模型适应范围不一，关键参数通常需要根据工况进行校正；同时，实验通常难以完全模拟工况。

为得到较为准确的流道寿命预测结果，下文将结合冲蚀实验和数值模拟进行流道冲蚀寿命和倾角优选的研究。

2 理论冲蚀模型

本文采用ANSYS-FLUENT 中的冲蚀模型，见式（1）。该模型简洁且结果便于与失重法测量的实验数据进行对比，所得结果为单位面积单位时间内去除的材料质量。

模型中，速度和粒径参数值在此类冲蚀模拟中一般取C=1.8×10−9，b=2.6[17-18]。为得到准确的模拟结果，通过实验数据选取合适取值。

模型设置中还包括冲击角和壁面反弹系数。不同冲击角下粒子对壁面的冲击效能不同，该参数多以分段线性函数定义，取适用于石英砂与碳钢的分段线性冲击角函数[19]，见表3。

图6 圆形流道试件及流道偏心倾角Fig.6 Circular channel specimen and inclination diagram

表3 冲击角参数设置Tab.3 Impact angle parameter setting

壁面反弹系数，其物理含义为碰撞前后速度分量的比值，表示粒子碰撞壁面的能量交换和损失[20]。本文采用的壁面反弹系数为

3 圆形偏心携岩流道冲蚀实验

3.1 实验设备及实验流程

由于主要观察流体对转折处的冲蚀作用，且流道为对称结构，故试件选择为完整流道的一半。选择与钻井机器人相同的材料制作流道样品，并在转角处设置法兰连接便于观察，流道偏心倾角为5°，如图6 所示。

由于本次实验的主要目的在于校验冲蚀模型和观察冲蚀位置形态，试件直径对实验结果的影响不大，可以忽略，所以本次实验为了降低成本，试件选用了与钻井机器人材料相同的现成管材，没有再进行机械加工，样件内径为17.4 mm，略小于20.0 mm。图7 所示为搭建的由泥浆泵、水箱、循环管路组成的实验台架，试件安装于实验台，如图8 所示，实验流程如图9 所示。

实验过程为循环操作，试件安装完成后，启动泥浆泵和水箱中的搅拌器，冲蚀到达设定时间后停泵拆下试件，期间搅拌器不停，防止泥沙沉降。

拆下的试件用清水冲洗静置相同时间后，用高精度电子秤称重，用游标卡尺测量各法兰端面的内径，记录数据并重复实验。

图7 实验台架实物图Fig.7 Experimental facility

图8 试件安装效果Fig.8 Specimen installation effect

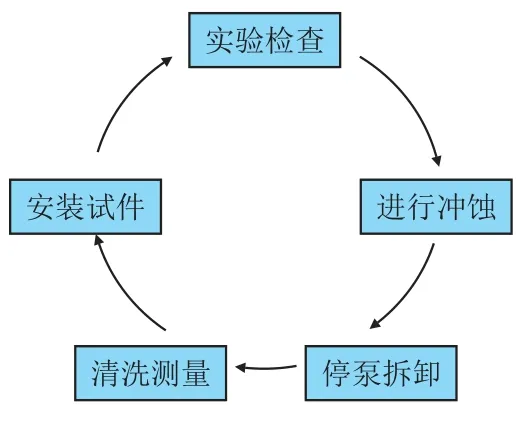
图9 实验流程Fig.9 Experimental process

3.2 实验冲蚀点的冲蚀规律

试件流道转折处采用法兰连接，将两个转折处分为4 个测量面，每个测量面取两个相互垂直的测量方向，观察测量流道截面的变化，各测量面位置如图10 所示；各面选取两个正交的测量方向如图11所示，各测量面的不同测量方向的数据在图12 中以测点1-1、1-2 的方式标出，第一个数字表示测量面位置，第二个数字表示测量方向。

在实验过程中，可明显地观察到法兰连接面出现的冲蚀现象。图11 所示为冲蚀较为明显的测量面2，实验初期约3 h 后的情况见图11a，此时法兰连接面出现较为明显坡状冲蚀痕迹，随着实验的进程，冲蚀坡逐渐加深加长，在冲蚀进行到约90 h 后，冲蚀坡由外向内发展至深处，冲蚀边界明显，如图11b所示，冲蚀坡最深处长度约为16.88 mm，深度约为1.35 mm。

图10 测量面示意图Fig.10 Schematic diagram of measuring surface

图11 测量面2 冲蚀前后对比Fig.11 Contrast before and after erosion of measuring surface 2

冲蚀转角处不同测量面，不同方向的冲蚀量不同。测量面1 和测量面3 口径变化相对较小，相对冲蚀损失量小；测量面2 和测量面4 则冲蚀损失量略大。

对各测量面的不同测量方向的端面内径进行测量，如图12 所示。

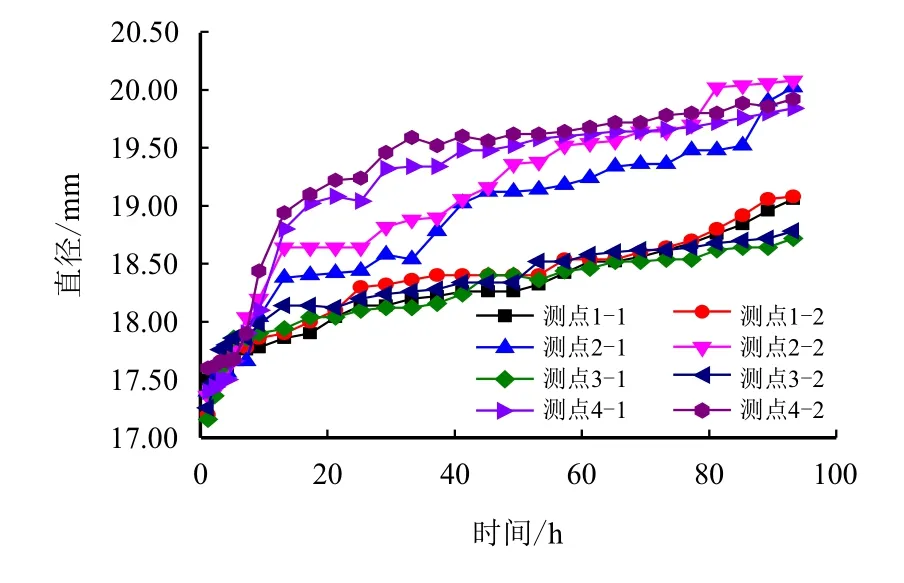
图12 各测点端口直径-时间关系图Fig.12 Diameter of port vs.time of each measuring point

总体上，在实验前10 h，各处口径增长较快，随后继续缓慢增加。但沿流速方向转角的测量面，即测量面2，测量面4 的冲蚀损失始终大于前侧。由图11，图12 可知，转角处的冲蚀点沿周向分布不均，总体上在转角外侧较为集中，流道冲蚀后形状逐渐趋近于偏心喇叭形，在流道设计时应予以考虑。通过游标卡尺测量发现，流道深处内径变化相对于测试面附近小得多，故偏心携岩流道转角处的质量损失最大，是流道冲蚀损失的主要部分。

3.3 冲蚀速率分析

冲蚀对样件整体造成的质量损失随时间的关系如图13 所示，呈近似线性；根据失重计算冲蚀速率，得到冲蚀速率散点图如图14 所示。

由于实验条件和测量误差，试件的冲蚀速率存在一定波动，通过曲线拟合可以发现冲蚀速率逐渐趋于稳定，与测量面的口径变化规律一致，所得试件的冲蚀速率为10.0∼25.5 mg/(m2·s)。

图13 总重量随时间变化图Fig.13 Diagram of total weight vs.time

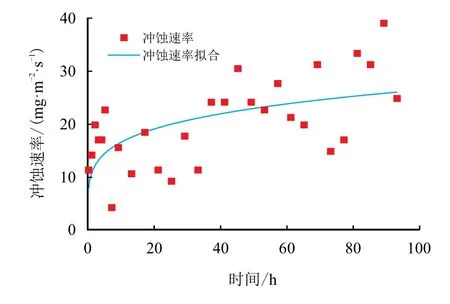
图14 冲蚀速率-时间关系图Fig.14 Diagram of erosion rate vs.time

4 数值模拟研究

4.1 计算模型设置

根据实验试件的实际尺寸，建立仿真模型，其流体模型示意图见图15。流道转折处前段长度超过了内径的3 倍，保证了进入转折处流体能充分模拟实际情况。

图15 流体模型示意图Fig.15 Fluid model diagram

采用欧拉-拉格朗日方法建立流动模型，由于流量大，内径小，采用Realizablek−ε 湍流模型；对流体区域采用高质量结构化网格划分，测得最终节点数为27 556，网格单元数为24 163。

4.2 边界条件设置及模型参数计算

根据所设定的冲蚀模型，模型由式（1）定义。壁面边界条件参数设置由式（2）及表3 决定。实验中出口压力经计算约为0.9 MPa，设为压力出口；打开DPM（离散相）模型，设置固相注入，根据实验中含砂量波动约0.3%∼0.5%，对应调整注入固相的质量流量，其他实验参数如表4 所示。

表4 模拟参数Tab.4 Simulation parameters

在含砂量分别为0.3%、0.4%和0.5%条件下，独立调整粒径参数和速度参数进行数值模拟，验证不同模型参数在相同实验条件下的冲蚀速率，所得冲蚀速率变化见图16，图17。

图16 粒径参数与冲蚀速率关系图Fig.16 Relation between particle size parameter and erosion rate

图17 速度参数与冲蚀速率关系图Fig.17 Relation between velocity parameter and erosion rate

由图16、图17 可见，粒径参数与速度参数对模型的结果均有明显影响。根据前人所做研究可知，颗粒粒径对冲蚀影响更为显著[21-22]，同时在实验中流量相对稳定，流速与理论值差距不大，粒径参数应是实验中影响冲蚀速度的主控因素。故本文选择以调整粒径参数，完成实际尺寸流道的冲蚀寿命数值模拟和选择最佳偏心倾角，取数值模拟结果在冲蚀速率区间（图16 中阴影范围）的两次模拟取值的中间值，最终选取的参数为C=2.25×10−10，b=2.6。

4.3 流道冲蚀倾角优选及寿命计算

钻井机器人三段式偏心携岩流道最终结构如图18 所示，在设计壁厚5 mm，出口压力60 MPa，含砂量0.5%，粒径0.08 mm 情况下，通过前文确定的模型参数和结构参数，得到如图19 所示的三段式偏心携岩流道冲蚀云图。

图18 三段式偏心携岩流道结构模型Fig.18 The structural model of eccentric entrainment channel

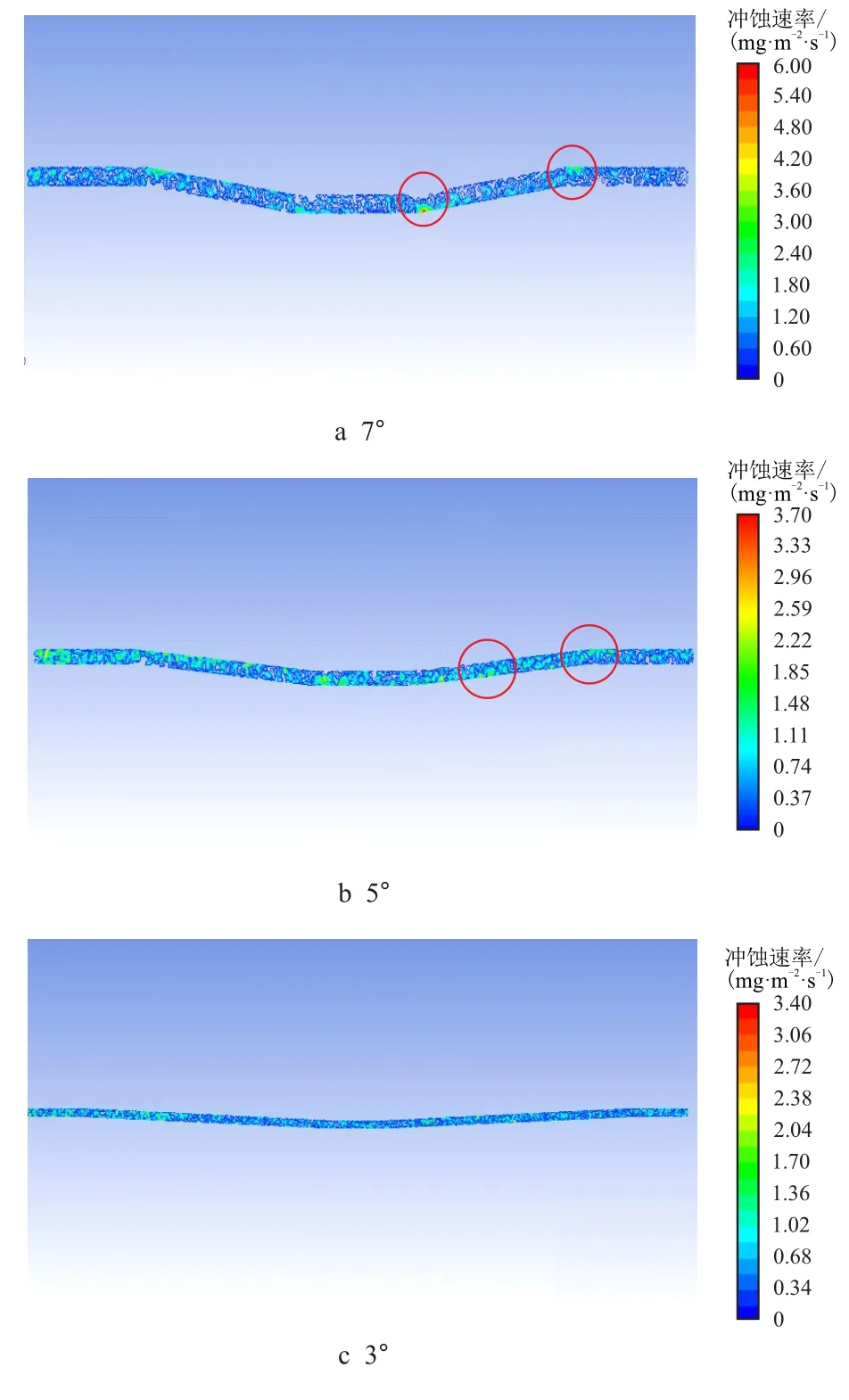
图19 三段式偏心携岩流道倾角对冲蚀的影响云图Fig.19 Cloud map of influence of offset erosion on inclination angle of eccentric camshaft

由图19 可见，三段式偏心圆形流道的冲蚀较为集中的位置为流道转角处外侧，且沿周向分布不均；且倾角越大，冲蚀点集中越明显，冲蚀位置和效果与前文实验一致。同时偏心携岩流道倾角对水力压降影响不大，具体结果如表5 所示。

表5 不同倾斜角度仿真结果数据Tab.5 Simulation results of different tilt angles

结合前文分析，冲蚀主要表现形态为坡坑减薄，考虑流道材质的变化，冲蚀对壁面的减薄速率为

故对管道冲蚀寿命计算可采用壁面冲蚀坑深度的时间积累表示

通过以上寿命量化方法，将式（1），式（3）和式（4）联立，并取最大冲蚀速率，可得流道冲蚀寿命计算公式[23]如下

利用式（5），结合冲蚀的数值模拟结果，计算出了不同倾角参数下流道的最大工作时间，得到倾角与流道最大工作时间的变化规律，如图20 所示。

由图20 可知：（1）随着三段式偏心携岩流道倾角的增加，流道冲蚀速率增大，流道最大工作时间减小。（2）流道偏角与剩余空间成正比，流道偏心部分需要尽可能多的空间安装控制模块，故在满足耐用性条件下选择尽可能大的偏角。当偏心携岩流道相对于水平段流道轴线倾角大于6°时，数值模拟钻井工况下最大工作时间低于300 h，未达到一般井下工具（如MWD，螺杆等）的工作寿命，不利于钻井机器人的应用，综合考虑钻井机器人内部的空间需求，选择偏心圆形流道最佳倾角为5°。

图20 圆形偏心携岩流道倾角对最大工作时间的影响Fig.20 Influence of offset erosion on inclination angle of eccentric camshaft

5 结论

（1）通过分析微小井眼水平井连续油管钻井机器人的发展现状和要求，提出了能同时解决连续油管水平井钻井屈曲和提升自动化能力的钻井机器人方案，其中钻井机器人内部偏心携岩流道设计是一个难点。

（2）结合机器人的尺寸要求，设计出了多种流道方案。通过分析，中置圆形流道不满足空间需求；弯月形流道易冲蚀损坏；圆环形流道压耗大；椭圆形流道目前加工困难，偏心圆形流道是现阶段可行的最佳流道方案。

（3）分析偏心圆形流道不同当量直径对携岩压耗的影响，结果表明：钻井机器人流道内径与压耗呈反比，且当内径小于20 mm 时压耗陡升，综合空间需求，20 mm 为可选最小流道直径。

（4）采用了数值模拟-单元实验-数值模拟的研究方法，搭建了实验台并进行了冲蚀实验，得到了在实验参数下的实际冲蚀速率；同时发现冲蚀主要集中于偏心流道转角处后侧，且冲蚀流道截面形状呈偏心喇叭状。

（5）通过实验数值对模型进行参数修正；采用粒径参数为C=2.25×10−10，速度参数为b=2.6。最终对完整三段式偏心流道进行冲蚀数值模拟研究，明确了倾角与冲蚀寿命的规律。在壁厚5 mm，倾角为5°条件下，流道的工作寿命超过300 h。模拟的主要冲蚀点位置和形态与实验一致，验证了最终模型的准确性以及三段式偏心携岩流道设计的可行性，为钻井机器人进一步设计和其他井下工具携岩流道设计提供了参考。