MCM 法和GUM 法评定氨气检测仪示值误差不确定度的对比

王海斌，张建宏，朱天一

（1.中国人民解放军92609 部队，北京 100077； 2.中国兵器工业集团第五三研究所，济南 250031）

氨气是一种无色、有强烈刺激性气味的气体，极易溶于水，广泛应用于化工、轻工业、国防、制药、化肥、合成纤维等领域，是一种重要化工基础材料。氨气具有毒性，能灼伤皮肤、眼睛、呼吸器官的粘膜，人吸入过多，会导致肺肿胀，甚至死亡［1］。氨气在空气中的爆炸低限含量(LEL)为16.1%，泄露氨气可导致中毒，对眼、肺部粘膜、或皮肤有刺激性，有化学冷灼伤危险。因此在与氨气相关的场所必须安装有报警功能的氨气检测仪，对空气中氨气浓度进行实时检测，避免爆炸、中毒等事故的发生。

氨气检测仪的检测原理包括电化学分析法、分光光度法、气相色谱法、离子色谱法、氨气敏电极法等，目前用于现场监测的氨气检测仪主要采用基于电化学分析原理的电化学传感器。电化学传感器随着时间的推移，会出现电解质损耗、电极钝化等现象，造成检测仪示值漂移、误差过大等问题，严重影响测量结果的准确度，埋下安全隐患。为了保证氨气检测仪测量数据的准确可靠，必须对氨气分析仪和报警器进行周期检定和校准。

测量不确定度和溯源性对于确保测量可靠性至关重要。ISO／IEC 17025 《实验室管理体系检测和校准实验室能力的一般要求》中规定了测量不确定度和溯源性是分析测量应用的重要前提［2］。目前在氨气检测仪校准过程中，示值误差不确定度的评定主要依据IOS／IEC 指南98–3：2008 《测量不确定度 第3部分：测量不确定度表示指南》 (采用“不确定度传播律”得到被测量估计值的测量不确定度的方法，简称GUM 法)［3–4］。近年来，为了克服GUM 法评定方法自身理论假设和近似的不足，逐渐发展起来蒙特卡罗(MCM)模拟的方法作为传统GUM 法不确定度评定方法的补充［5］。MCM 法是一种数值模拟方法，基于概率分布传播，进行分量合成或模拟，实现对不确定度的评定，具有不受非线性模型的限制、不必计算偏导数和有效自由度等优点［6］。MCM 法已经在物理量测量、化学检测中得到较为广泛的应用［7–17］。基于上述分析，笔者采用MCM 法借助MCM Alchimia 软件进行氨气检测仪示值误差的不确定度分析，并与GUM 法得到的结果进行对比研究。

1 校准过程与数学模型

待仪器通电预热稳定后，连接好气体管路并使用流量控制器稳定保持通入气体的流量，通入零点气体校准报警器的零点，通入满量程80%的氮中氨气体标准物质校准报警器的示值。通入满量程50%的氮中氨气体标准物质，观察报警器的读数，待读数稳定后，记录仪器读数，重复测量6 次，计算6 次读数的算术平均值，作为报警器示值。计算示值与标准气体浓度值的差值，差值与标准气体浓度值的比值即为报警器的示值误差。仪器的示值误差按式(1)计算。

2 基于GUM 法的测量不确定度评定

GUM 法基于中心极限定理，即大量的独立随机变量之和近似服从于正态分布，假设测量结果服从正态分布且模型可表示为若干线性模型之和的形式，通过不确定度传递率计算合成标准不确定度，从而得到被测量估计值的测量不确定度。

GUM 法评定测量不确定度主要包括如下步骤：（1）分析不确定度来源并建立测量模型；（2）通过对灵敏度、测量模型中各输入量的量化计算，给出其相应的不确定度分量；（3）将各分量合成计算得出合成标准不确定度；（4）确定包含因子k值并计算扩展不确定度。

式(1)测量模型中的输入量互不相关，因此合成标准不确定度按式(2)计算：

2.1.1 测量结果的重复性引入的标准不确定度u1

测量结果的重复性引入的不确定度可以通过连续测量得到的测量值，用A 类方法进行评定。对氨气检测报警器，选择150 μmol／mol 的标准气体，连续测量n次(n=6)，得到测量值分别为148、147、148、146、147、146 μmol／mol，计算得平均值：

2.1.2 仪器分辨力引入的标准不确定度u2

仪器的分辨力为1×10–6mol／mol，按照均匀分布考虑，k= 3，则仪器分辨力引入的标准不确定度：

2.1.3 环境条件变化引入的标准不确定度u3

在规程规定的环境条件下开展检定工作，环境条件变化对测量结果的影响很小，因此环境条件引入的不确定度u3可以忽略不计。

2.1.4 流量稳定性引入的标准不确定度u4

在规程规定的流量下通入气体标准物质，使用的流量计准确度为4.0 级，调整转子在400 mL／min 的刻度线上，使用流量标准装置多次测量400 mL／min的流量，流量变化范围一般不超过10 mL／min，对测量结果的影响不超过分辨力1 μmol／mol，按照均匀分布，k= 3，则流量稳定性引入的标准不确定度：

2.1.5 读数引入的标准不确定度u5

读数引入的不确定度主要是读取数值误差引起的，根据日常经验，读数误差不大于仪器分辨力，其引入的不确定度视为均匀分布，k= 3，则读数引入的标准不确定度：

2.2 输入量c0 引入的标准不确定度

输入量c0引入的标准不确定度主要来源于标准气体的定值不确定度，根据证书给出的定值不确定度来评定，因此采用B 类方法评定。标准气体是国家二级标准物质，量值为150 μmol／mol，相对扩展不确定度为2%，k=2，则输入量c0引入的标准不确定度：

2.3 合成标准不确定度

2.4 扩展不确定度

取包含因子k=2，则扩展不确定度：

2.5 不确定度评定结果报告

示值误差测量结果的扩展不确定度：U=2.13%，k=2。

3 基于MCM 法的测量不确定度分析

为了克服GUM 法的不足，MCM 法受了到人们的关注。与GUM 法的不确定度传递的本质区别是：MCM 法采用概率分布传递的方法，将概率密度函数的离散抽样输入测量模型之中，通过模型计算，获得输出量的离散抽样值，进而由输出量的离散分布数值直接获取输出量的最佳估计值、标准不确定度和包含区间。

MCM 法评定测量不确定度主要包括如下步骤：（1）建立测量结果与影响因素之间的测量模型；（2）为各影响因素设置概率密度函数；（3）选择蒙特卡洛模拟采样量的大小M，从输入量的概率密度函数中抽取M个样本值，计算相应输出量；（4）得到M个输出量分布函数的离散表示，由此计算输出量的估计值和不确定度。该方法计算过程如图1 所示。

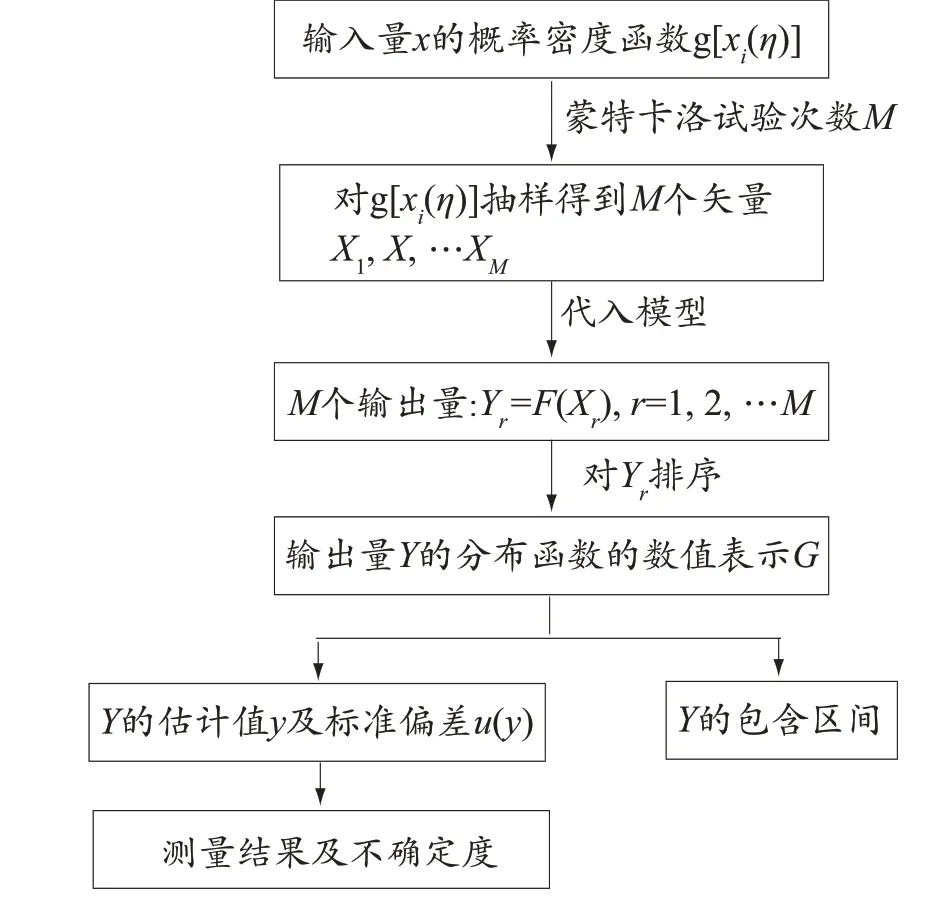
图1 蒙特卡洛法计算不确定度流程图

MCM Alchimia 是一款基于蒙特卡罗模拟的通用计算软件。通过MCM Alchimia 软件进行不确定度计算，采用的计算方法与JJF 1059.2–2012 《用蒙特卡洛法评定测量不确定度》［18］、JCGM 101：2008［19］一致。

3.1 蒙特卡洛模型的建立

根据校准过程与测量模型，得到氨气检测仪示值误差计算过程的函数关系，将函数关系输入到MCM Alchimia 软件中，建立测量不确定度评估的蒙特卡洛模拟模型。

蒙特卡洛模拟模型方程列于式(3)～(7)

3.2 MCM 模型中各参数的输入

设定已建立的蒙特卡洛模型的采样次数M分别为5×105，1×106，2×106，并将各参数的概率密度函数和仪器校准时的参数输入到模型之中，见表1、表2。

表1 概率密度函数

表2 仪器校准参数

3.3 模拟结果

通过MCM Alchimia 模拟运算得出的氨气检测仪示值误差的测量不确定度结果，不同模拟次数的MCM 概率分布如图2～图4 所示。

图2 M=5×105 时的MCM 概率分布图

图3 M=1×106 时的MCM 概率分布图

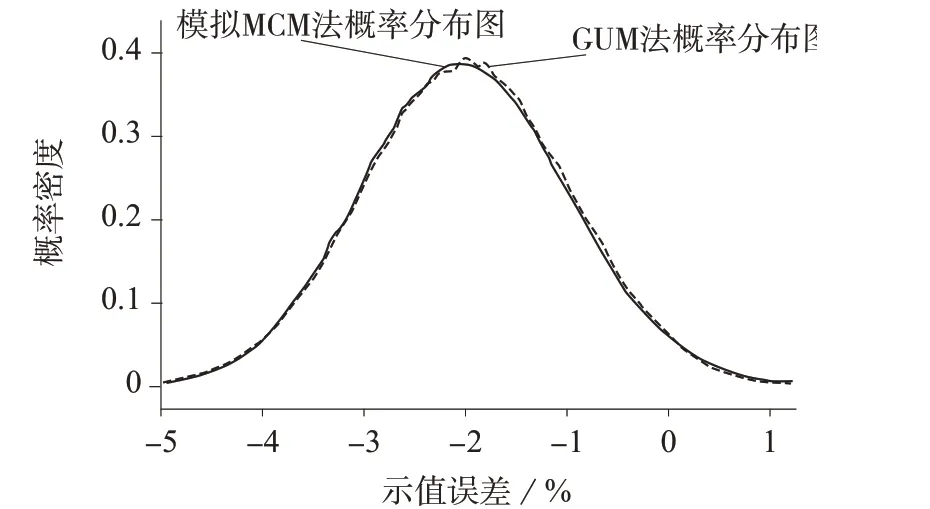
图4 M=2×106 时的MCM 概率分布图

图2～图4 概率分布图显示，三种次数模拟的结果均与理论正态分布吻合较好，曲线的平滑度随模拟次数增加而增大，当模拟运算为5×105次时，曲线“毛刺”较多，平滑度不如更高次数，但总体而言三种模拟次数得到的曲线结果差距较小。

此外，GUM 法基于中心极限定理的正态分布假设，因此正态分布曲线可近似为GUM 法曲线，由此可以得出，随着模拟次数的增加，实际模型与理论模型的拟合度逐渐增大，进而验证了GUM 假设的正确性，说明当模拟运算不小于5×105次时，MCM法和GUM 法的氨气检测仪示值误差不确定度评定模型具有一致性。

两种方法计算得到的测量不确定度结果列于表3。当模拟次数达到1×106后，随着模拟次数的增加，标准不确定度不变，表明模拟结果已经达到统计学意义上的稳定，模拟结果可信度较高。

表3 测量不确定评估结果

由表3 可知，对于标准不确定度，MCM 所得结果小于GUM 所得结果，且MCM 的包含区间比GUM 的包含区间范围要窄一些。其可能原因：（1）在GUM 法中，测量重复性引入的不确定度包含了测量模型自变量导致的部分不确定度；（2）GUM 假设各个自变量不相关，GUM 法保守估计了这些量值，这导致测量结果增加了一些不可靠的测量不确定度。相比之下，MCM 法对各因素考虑较为全面，所得的不确定度置信区间更窄，结果更符合客观事实，可信度更高。

4 结语

分别利用GUM 法和MCM 法评定了氨气检测仪示值误差的测量不确定度，两种方法均适用于氨气检测仪的示值误差模型。但GUM 受理论的局限和缺陷影响，计算结果偏高，不确定度评估趋于保守。而利用MCM Alchimia 软件进行的蒙特卡洛方法评定，具有硬件要求低、编程简单、通用性强、不需要计算复杂积分等优势，所得结果更接近实际，适用于氨气检测仪示值误差的测量不确定度评定。