用电阻定义式求特殊电容器直流电阻

黄绍书，冯俊杰

(1. 六盘水师范学院，贵州 六盘水 553000；2. 六盘水市第八中学，贵州 六盘水 553004)

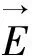
这一常规的计算方法，由于电流密度J和电场强度E的矢量性，在实际计算过程中还是比较麻烦的，特别是对于一些特殊形状的电容器电阻的计算就显得更为突出.

1 特殊电容器电阻的计算

1.1 球冠形电容器

如图1所示，设球冠的高为H，对应的球半径为R，最大圆半径为r，最大圆的直径两端与球心连线的夹角为φ，那么球冠的面积为

图1 球冠形电容器

(1)

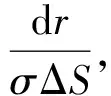
图2 两个同心球冠构成的电容器的截面图

(2)

即

(3)

因此，整个球冠形电容器的电阻为

(4)

当φ=2π时，球冠形电容器就过渡为球形电容器.这时，式(4)可简化为

(5)

很显然，式(5)即为球形电容器的电阻表达式.

1.2 柱冠形电容器

若柱冠的长为L、半径为R、圆心角为θ，那么，柱冠的面积可表示为

S=LRθ

(6)

如图3所示是内、外柱面半径分别为R1和R2、长为L、圆心角为θ的同轴柱冠形电容器示意图.设两柱冠之间充满电导率为σ的电介质，同样可将两柱冠之间的介质层看作是由许多同轴的厚度为dr的薄介质柱冠串联组成，而每一个薄介质柱冠又同样相当于由许多面积为ΔS的方柱体形电阻元并联组成.

本文研究了带有噪声的等级群体,通过伊藤公式、比较定理和数学归纳法,证明了噪声强度足够弱时,群体可以无条件达到群集运动。本文研究的等级群体是基于全局领导者速度是匀速时分析的,对领导者变化速度的情形有待进一步研究。

图3 同轴柱冠形电容器示意图

(7)

即

(8)

因此，整个柱冠形电容器的电阻为

(8)

当θ=2π时，柱冠形电容器就过渡为圆柱形电容器.这时，式(9)可简化为

(10)

很显然，式(10)即为圆柱形电容器的电阻表达式.

1.3 正多棱柱形电容器

如图4所示，设正n(n∈N且n>2，下同)棱柱形电容器高为H，每个侧面与轴之间的距离为R，相邻两条棱对轴的张角为φ，那么棱柱的每个侧面面积为

图4 棱柱形电容器

(11)

如图5所示是正n棱柱形电容器的截面示意图.设内、外两侧面之间充满电导率为σ的电介质，内、外两侧面与轴之间的距离分别为R1和R2.将两侧面之间的介质层看作是由许多同轴的厚度为dr的薄介质层串联组成，而每一个薄介质层又相当于由许多截面积为ΔS的方柱体形电阻元并联组成.

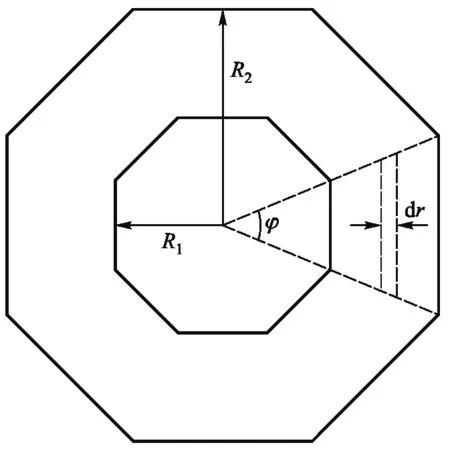
图5 棱柱形电容器的截面示意图

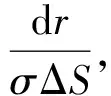
(12)

即

(13)

所以，每个等腰梯形状电容器的电阻为

(14)

显然，正n棱柱形电容器的电阻为n个相同的等腰梯形状电容器的电阻并联的等效电阻.即

(15)

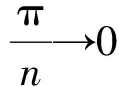
(15)

即简化为

(16)

很显然，式(16)与(10)是一致的.这就说明，当n→∞时，正n棱柱形电容器就过渡为圆柱形电容器.

2 结语

本文对特殊形状的电容器电阻的计算方法的主要特点在于直接应用电阻的串联和并联关系，简洁明了的简化了计算过程，并使知识回归本源.

有文献[12-15]采用与此类似的方法对一些特殊形状的电容器电容进行了计算，同样收到化繁为简的效果.