刚体一般运动的描述

邵瀚雍

(北京师范大学 物理学系，北京 100875)

一般运动是刚体运动学中最复杂的问题，因此国内的理论力学教材大多对此介绍较少. 且由于刚体运动学教学难度大，课时少，故多数同学跳过了刚体一般运动的内容，但这恰是将刚体运动转化成代数知识的极佳机会，不得不说是一种遗憾.

事实上，刚体的一般运动总能分解成基点的运动和绕过该点某轴线的定轴转动，国外教材对此用代数语言给出了证明，但也没有就代数理论和刚体运动的关联进行深入的探讨.

本文从正交矩阵讲起，力图用清晰简明的语言，论证使用矩阵描述刚体运动的合理性和优越性，并借用代数思想，将刚体运动和线性代数的知识联系起来，希望能对理论力学的相关教学和学生的学习起到一定的补充和帮助作用.

1 参考系

实验室参考系，即观者所在的惯性参考系；本体参考系，即固连在刚体上，并与之共同运动的参考系，一般是非惯性系.

固连在两种参考系上的坐标系各有利弊. 在实验室坐标系中，基矢对时间的微商为零，便于建立动力学方程，但许多力学量在该系中较复杂并不断变动；在本体坐标系中，这些力学量虽然直观简单，恒定不变，但其坐标轴的基矢处在变动之中.

在研究刚体定点转动的问题时，我们需要寻找这两种系之间的关联，恰当使用它们描述刚体的运动[1].

2 刚体的一般运动

刚体在空间不受约束自由运动时，其自由度s=6. 一般选定广义坐标(xc,yc,zc,φ,θ,ψ)描述刚体的状态，其中xc、yc、zc为刚体质心在实验室系中的笛卡尔坐标，φ、θ、ψ为刚体的本体系和实验室系坐标变换对应的欧拉角.

刚体一般运动有4类特殊情况：平动、定轴转动、平面平行运动、定点转动. 虽然它们形式各异，但可以证明如下两点[2]：

1) 定点转动总可以等效于绕过该定点某一轴线的定轴转动.

2) 刚体一般运动总可以分解为某点的运动和绕过该点某轴线的旋转.

换言之，总可以将复杂的一般运动，分解成过一点的定轴转动(或由多个定轴转动合成)与该点的运动.

第1点所谈到的内容，正是刚体运动欧拉定理. 该定理指出，对于基点固定的刚体，其运动可以分解为绕某个或多个转轴的转动. 根据欧拉运动定理，我们可以将之推广，即第2点，沙勒定理. 该定理指出，刚体的最广义位移等价于一个平移和一次旋转. 它们是本文的重点，在证明前，需要先通过代数的语言，合理描述刚体的运动，以便于后续的证明.

3 正交矩阵

在线性代数理论中，正交矩阵A被定义为行向量、列向量皆正交且值为1的方阵[3]，即满足如下的性质(E为单位阵)：

ATA=AAT=E

(1)

矩阵乘法等价于一次线性变换，换句话说，在数学里这种特殊的变换(正交变换)可以保持空间中任意两点的欧式距离不变. 这意味着若将某向量v乘上正交矩阵A，得到的新向量长度不变，且空间的原点不变. 我们通常将这种变换称为欧拉变换[4].

此外，由于正交矩阵满足：

ATA=A-1A=E

(2)

正交变换一定存在逆变换，而且该逆变换很容易写出：A-1=AT. 正交矩阵的这些特殊性质在描述刚体运动时展现出极大的优越性，因此，我们常用它描述刚体运动.

4 刚体运动的代数表达[2]

从物理上讲，根据沙勒定理，刚体的运动可以分为两种：定点转动和点的运动. 也就是第2节中提到的6个广义坐标. 而上一节中提到的正交变换——欧氏距离不变的线性变换，恰好可以准确反映刚体的定点转动. 换言之，刚体的定点旋转过程可以由一次欧拉变换来描述. 容易得知，这种变换对应的正交矩阵R应是一个含时矩阵，即R(t).

仅仅描述旋转过程是不够的，还需要描述点的运动. 易知，描述该运动只需在旋转后添上一个简单的平移矢量p即可.

从数学上讲，刚体的运动，可以反过来看作是坐标轴的运动. 因此，假设两组正交基分别为[e1,e2,e3] 和 [e′1,e′2,e′3]. 在这两组基下，某向量v在这两组基下的值分别为[a1,a2,a3]T和[a′1,a′2,a′3]T.

因此有

(3)

于是，得到

(4)

已知a=[a1,a2,a3]T，a′=[a′1,a′2,a′3]T且定义如下：

(5)

则可以将上式写为

a=Ra′

(6)

称R是旋转矩阵. 可以看到，R矩阵是由两个标准正交基相乘而来，在线性代数中可以很容易证明，这样得到的矩阵R是正交矩阵，或者反过来说，任何正交矩阵都可以拆分为两个标准正交基的矩阵乘积.

因此，旋转矩阵R恰好是正交矩阵，而正交矩阵对应的变换也恰好是两组基之间的旋转变换，也就是实验室系和本体系的欧拉变换；并且，任意实正交矩阵都能看作为一个旋转矩阵. 值得一提的是，旋转矩阵的集合称之为特殊正交群：

SO(n)={R∈n×n|RRT=E，detR=1}

这个正交群可以描述n维空间的旋转变换，在此只考虑n=3的情况.

再考虑定点的运动，可以将刚体的运动在数学上表示为

a′=RTa+p

(7)

数学的正交矩阵(变换)，对应着欧式空间中距离不变的线性变换，而物理的旋转矩阵(旋转)，对应着刚体运动时的任意两点保持相对距离不变的属性. 这样，在本节和上一节中已经论证了刚体运动的代数表达，这种代数的表达方式是相当合适且严谨的.

5 旋转变换的本征问题

刚体的定点转动定理指出，对于基点固定的刚体，其一般运动都可以分解为绕某个或多个轴的转动.

根据定理，假设转轴对应的空间列向量为p，由于转轴并不会因为刚体转动而发生任何变化(刚体本身就在绕轴转动)，因此，当发生旋转变换时，p应当保持不变. 这对应着数学中的不变子空间理论. 请看定理[4]：

设φ是线性空间V上的线性映射(变换)，而总能找到V的子空间U，使得

φ(U)⊆U

即子空间U的任意元素p在线性映射φ的像Imφ中依然是p本身，称U为φ的不变子空间.易得，φ总有两种特殊的不变子空间U，分别是零子空间和全空间V，并称之为平凡子空间.

可以发现，在三维旋转映射R下，有一个我们最关注的非平凡不变子空间，这个子空间恰好就是转轴所处直线对应的子空间.

上述内容也可以在拓扑理论中理解成映射的不动点原理(Brouwer’s Fixed-point Theorem).

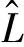
(8)

因此，由Rp=1p，得知p为旋转变换φ的本征函数，λ为变换φ的本征值，这恰好就是线性代数中熟知的矩阵特征值问题：

Ap=λp

(9)

所以若要证明欧拉定理，可以将定理的证明等价于证明旋转矩阵R的特征值组中必然有一特征值λ1=1.

本征值与本征函数对刻画线性系统的普遍性质和演化规律有着重要意义. 它是所有线性体系中最根本的特点. 如果能得到线性体系对应的本征值与本征函数，就可以通过线性组合的方法描述或解释这一体系更为普遍的规律.

6 欧拉运动定理的证明和推论

欧拉运动定理的论证过程在H.Goldstein所著的Classical Mechanics[6]和Beatty M.F. 所著的Principles of Engineering Mechanics: Kinematics中都有着详细的描述. 两本书巧妙利用矩阵和线性代数理论证明了欧拉定理，而我们的证明过程也借鉴了其中的思想.

设旋转矩阵为R，欧拉定理中所描述的轴线为p，则有：Rp=p.

根据上一节中内容，若需要证明旋转过程中存在始终不变的轴线p，则等价于证明矩阵R具有特征值λ1=+1.

容易证明旋转矩阵R为正交矩阵，所以由RTR=RRT=E，可得：

(R-E)RT=E-RT

(10)

|R-E||RT|=|E-RT|

(11)

设旋转前后两组正交基的基点重合于刚体的定点，且初始基为标准正交基. 则可以得出初始旋转矩阵为三阶单位阵E.因此，根据矩阵乘法，后续的旋转矩阵的行列式的值|R|和|RT|仍为+1.

由式(11)可得

|R-E|=|E-RT|=|E-RT|T=|E-R|

(12)

因此，有

|R-E|=|E-R|=|-1(R-E)|

(13)

而

|-1(R-E)|=(-1)n|R-E|

(14)

其中n为矩阵维数，也是空间维数. 所以得到

|R-E|=(-1)n|R-E|

(15)

刚体所处为三维空间，n=3，所以

|R-E|=-|R-E|=0

(16)

最终得出|R-E|=0，即矩阵R至少有一个特征值λ1=+1，欧拉运动定理得证.

需要多谈两个问题：

其一[1]，如果刚体所处空间不为奇数维度，而是偶数维度，则得不到|R-E|=0的结论，也就是说欧拉运动定理在二维、四维等偶数维空间失效. 所以，平面内不存在欧拉定理，因为当坐标系转动时，任何位于平面内的矢量均会发生改变，唯有沿转轴方向的矢量不发生改变，但此时它与平面垂直，并不在平面内.

这是一个相当有意思的推论，这意味着我们所处的三维空间并不是随便确定的.

其二，是旋转矩阵R是否还存在别的特征值？答案是肯定的. 利用矩阵的久期方程：

|R-λE|=0

(17)

可以发现，这是一个关于λ的三次方程. 高斯的代数基本定理指出，该一元三次方程在复数域中必然存在三个根. 在文献[7]中，我们可以根据矩阵的迹tr(R)求得另外两个特征值分别为

λ2,3=e±iΩ

(18)

也就是说，旋转矩阵的另外两个复特征值的辐角，恰好为欧拉定理中绕固定轴线p的旋转角Ω.

这里给出两个特殊情况：

1)λ1,2,3=+1：此时Ω=0，意味着刚体保持了初始时刻的状态，为平凡解.

2)λ1=+1;λ2,3=-1：此时Ω=π，意味着刚体绕轴转过了180°，刚体任意两点之间的矢量p′都做了关于p的空间坐标反演操作.

而沙勒定理是欧拉定理的一个直接推论. 该定理的证明如下.

刚体的一般运动可以分解为刚体中某一点的运动并叠加上刚体对该点的定点运动. 而根据欧拉运动定理，后一运动可以认为是绕过该点的某一轴线的转动. 因此，刚体的一般运动可以分解为某点的运动和绕过该点某轴线的旋转. 沙勒定理得证.

至此，我们完成了刚体一般运动中沙勒定理的证明，论证了刚体的任意运动都可以分解为某点运动和定轴转动.

矩阵语言虽然简练，但不能直观反映物理实质. 这里需要寻找一种物理的描述办法刻画刚体的运动，这就是所谓的欧拉角，也是前面所述的3个广义坐标φ、θ、ψ.

7 欧拉角

在天体和力学领域里，为了完备、清晰地刻画刚体运动，分别用了章动角θ、进动角φ和自转角ψ来描述.这些称呼来自陀螺的定点运动，如图1所示.

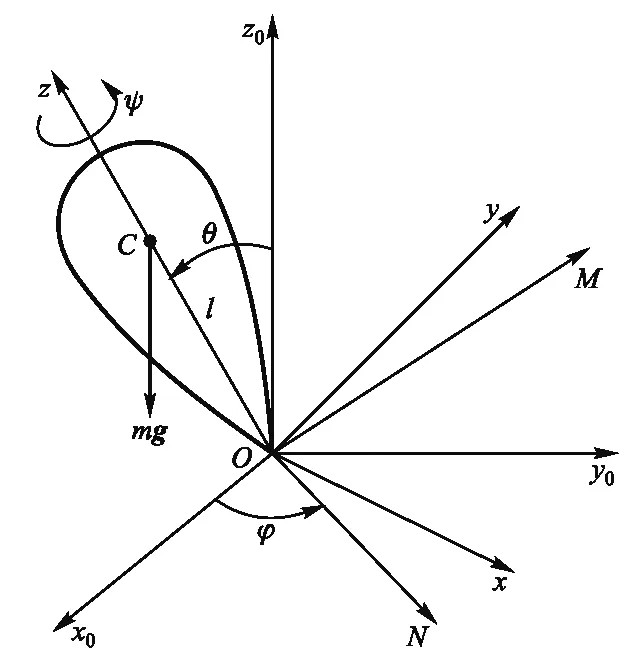
图1 陀螺定点运动示意图

为了便于描述欧拉角的具体意义，可将刚体的定点转动通过坐标轴的旋转，依次分成3个步骤，如图2—图4，这里在每个步骤后面都写上了对应的旋转矩阵R. 每一次的旋转并不是任意的，它们都可以在图1的陀螺运动中找到对应，转动顺序是进动、章动、自转，如下所示.

1) 绕Oz0轴进动φ：图2(a)→(b)

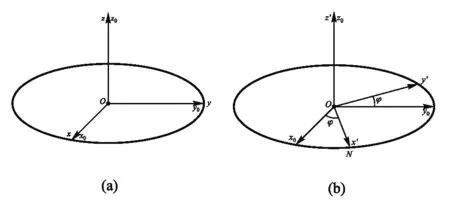
图2 进动示意图

从Ox0y0z0到Ox′y′z′的旋转矩阵为

(19)

2) 绕Ox′轴(节线ON)章动θ：图3(a)→(b)

图3 章动示意图

从Ox′y′z′到Ox″y″z″的旋转矩阵为

(20)

3) 绕Oz″轴自转ψ：图4(a)→(b)

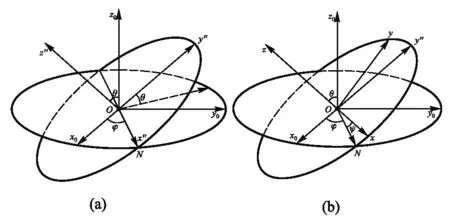
图4 自动示意图

从Ox″y″z″到Oxyz的旋转矩阵为

(21)

经过上面的三次旋转变换，可以得到描述刚体的任意旋转的总变换矩阵：

R*=RψRθRφ

(22)

由前面的结论可知，所有的变换矩阵都是正交矩阵，均由变换前后的两组基底相乘而来(此处为一组基的转置和另一组基之间的矩阵乘法).

(23)

将不同的角速度对应的基矢利用旋转矩阵得到的函数关系展开化简，可以得到如下的结论：

ω在实验室系的坐标轴投影为

(24)

ω在本体系的坐标轴投影为

(25)

这样，我们得到了刚体定点转动中绕某一轴线旋转的角速度ω的实际物理意义，即可以把这一定轴转动对应的转角Ω分解到3个有意义的欧拉角(也就是φ、θ、ψ)上去.

不过，需要强调的是，在导出欧拉角的时候，所经历的三次连续旋转的转轴的选取顺序其实存在着随意性. 只要每次选定的旋转轴不与上一次相同，便可以任意选取. 因此，在右手系中我们有3×2×2=12种不同的旋转方法，这称为欧拉角的顺规.

大多数的理论力学教材所采用的是x顺规，即第二次旋转绕x轴(前文中的节线ON)，而多数的量子物理、核物理的教材所采用的是y顺规，即第二次旋转绕y轴.

在工程中，为了弥补前两种顺规在变换前后的坐标系区分程度低的缺点，常采用第三种常见顺规：xyz顺规[2]，这样得到的3个角就分别是飞机的偏航角(Yaw)、俯仰角(Pitch)和滚动角(Roll).

8 总结

在本文中，我们介绍了正交矩阵在描述刚体运动的优越性，并将之应用到刚体的旋转运动中，随后利用旋转矩阵证明了刚体运动的沙勒定理，这意味着复杂的刚体一般运动可以由定轴转动和点的运动来描述. 之后，我们从物理给出了刚体定点运动的图像，并用欧拉角来描述这样的运动. 刚体的运动学在数学上和物理上都全部得以描述.