物理学中常用的高斯与类高斯型积分
王 蒙,陶俊琦,程剑剑,郑 华
(陕西师范大学 物理学与信息技术学院,陕西 西安 710119)
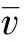
本文旨在基于大学数学基础对常用的高斯及类高斯型积分做系统的阐述,给出相应的求解方法和通用积分结果. 以期助力学生学习与教职人员教授相关内容.
1 高斯与类高斯型积分
本节中,我们将对不同的高斯与类高斯型积分进行计算与讨论,遵循由简到难、由特殊到一般的逻辑.
1.1 高斯型积分I=e-αx2dx,(α>0,α∈R)
在高斯与类高斯型积分中,非常重要的一个积分是

(1)
考虑α为实数的情况.为保证式(1)积分收敛,要求α>0. 式(1)无法利用牛顿莱布尼兹公式求出原函数对积分进行计算. 但可以通过构造的方法,建立式(1)与二维积分的联系,然后利用常用积分就可以计算了. 具体过程如下

(2)
对式(2)中r的积分进行变量代换,容易看出是一个指数函数积分. 因此
(3)
此积分过程中体现了一个重要的思想,在当前维度下如果解决不了问题时,可以发散性的将问题向高维转化.某些特殊函数的生成函数,也应用了这一思想,在此我们不做详细论述[7].
下面讨论3个常用的高斯型积分.
(a) 当α=1时,由式(3)可得
(4)
(b) 将式(3)的积分限变成0到正无穷,由式(3)的积分函数是偶函数可得
(5)
(c) 将式(3)的积分限变成0到正无穷且α=1
(6)
1.2 Γ函数与高斯型积分
Γ函数与高斯型积分具有直接的联系[8-10].在实变函数中,Γ函数的通常定义如下

(7)
Γ函数具有如下性质
Γ(x+1)=xΓ(x)
(8)
将Γ函数式(7)的积分变量t作积分变量代换,令t=u2.可得

(9)
为便于文章后面的讨论,将式(9)改写为
(10)
可见,当x=0时,式(10)右边为高斯型积分式(6),故有
(11)
这是我们熟知的结果.
1.3 高斯型积分
下面将考虑几个不同积分限的高斯型积分.

与高斯分布相关的物理量的计算中,很常用的一类积分为

(12)
当n为奇数时,由于被积函数为奇函数,可得

(13)
当n为偶数时,取n=2k(k为自然数),式(12)变成

(14)
我们将以k=1为例,通过3种方法来计算I(2),然后给出积分式(14)的通用公式.
(a) 计算积分I(2)常用的方法为分部积分法
(15)
已经利用了高斯型积分式(3)的结果.如果k值取更大,用分部积分法计算式(14)会比较繁琐.
(b) 另一种方法计算积分I(2),可以将α看成变量
(16)
此方法比分部积分法简洁,更重要的是其可以很容易给出积分式(14)的通用公式
(17)
双阶乘定义:(2n-1)!!≡1·3……(2n-3)(2n-1).
(c) 更简洁的方法是将I(2)与Γ函数式(10)联系,可得
(18)

(19)
最后的结果已经利用Γ函数的性质式(8).此方法避免了(b)中对α求导的过程.
综上所述,式(12)的积分结果为
(20)
其中k为自然数.
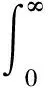
由上节可知,将高斯积分与Γ函数联系是很简洁的方法.与式(20)类似的过程可得
(21)
其中k为自然数.
1.4 类高斯型积分I=e-α(x+c)2dx
现在来计算类高斯型积分

(22)
其中α与c可以是复数,考虑到积分的收敛性,要求Re(α)>0. 这与1.1与1.3中要求α为实数不一样,我们称之为类高斯型积分.
由于类高斯型积分已经涉及到了复数,有些计算过程会用到“数学物理方法”中的留数定理[11].为使讨论更为清晰,我们分以下几种情况:
(a)α与c均为实数: 这种情况与1.1的讨论很相似,唯一的差别是高斯函数的对称中心在x=-c.可以通过积分变量代换将式(22)变成式(3)

(23)
(b)α为实数,c为纯虚数:这种情况下需要用到留数定理. 不失一般性的可以令c=ib,b为正实数. 在复平面上选择积分路径如图1所示.
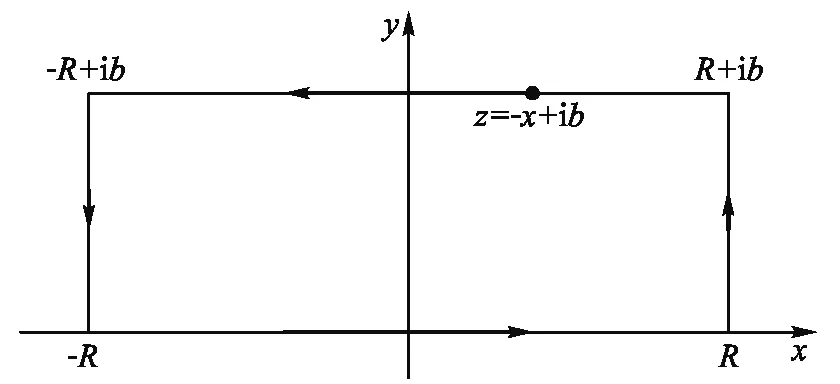
图1 复平面积分路径
被积函数f(z)=e-αz2在积分区域内是解析的.由留数定理可得
∮e-αz2dz=0
(24)
可将积分式(24)沿长方形闭合区域写成4部分之和
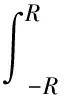

(25)
在R→∞,第三项与待求积分有简单的关系:
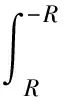
(26)
(27)
当b为负实数时,在复平面上将积分路径选在下半平面,其余过程与b为正实数类似,可以得到同样的积分结果.
(c)α为复数,c为实数:α为复数时,与1.1中α为实数时类似,可以得到
(28)

(29)
(d)α为复数,c为纯虚数:与1.4 (b)中计算过程类似并利用1.4(c)的积分结果,可得
(30)
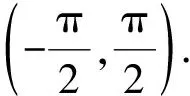
(e)α与c均为复数:此种情况是最一般的情况. 利用1.4 (a)中的积分变量代换,可以将复数c的实部消除,这时积分就变成了1.4 (d)中的积分. 因此,积分结果为
(31)
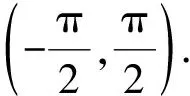

1.5 类高斯型积分I=eim(x+c)2dx



(32)
不失一般性的,先考虑m为正实数. 在复平面上eimz2解析,利用留数定理可得
∮eimz2dz=0
(33)
可在复平面上选择如图2所示积分路径.
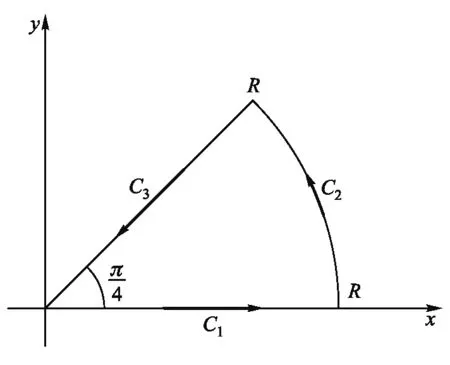
图2 复平面积分路径
可将积分式(33)写成三部分之和
(34)
当R→∞时,式(34)第一项为I/2, 其中I为待求积分;第二项积分为0,计算如下
(35)
第三项积分为
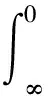
(36)
由式(34)可得
(37)
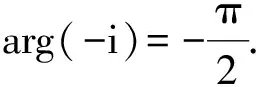
当m为负实数时,在复平面上将积分路径选在下半平面,其余过程与m为正实数类似.为方便,我们让m=-m′(m′>0),可得
(38)

(39)

(b)c为纯虚数:不失一般性的可以令c=ib,b为正实数. 在复平面上选择积分路径如图1所示,同1.4(b)类似有
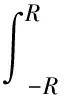

(40)
当R→∞时,式(40)第一项可以利用1.5(a)的结果,第三项等于负的待求积分,考察第二项与第四项的模可以发现总有一项是发散的. 因此,此种情况下待求积分是发散的.
(c)c为复数:此种情况是最一般的情况. 利用1.4(a)中的积分变量代换,可以将复数c的实部消除,这时积分就变成了1.5(b)中的积分. 同样的道理,此时积分是发散的.
1.6 高斯与类高斯型积分的讨论
通过观察式(3),式(31)与式(39)的积分结果,可以发现高斯与类高斯积分结果均可写成高斯积分结果的形式,只是需要限定α的辐角范围:
(a) Re(α)>0,α∈C,c∈C
(41)
需要限定arg(α)∈(-π/2,π/2), 注意α为实数时其辐角为0.
(b) Re(α)=0,α∈C,c∈R
(42)
需要限定arg(α)=-π/2或arg(α)=π/2.
2 高斯与类高斯型积分在物理学中的应用
为将上面讨论的高斯及类高斯型积分与物理学科中的实际问题联系起来,在此我们将选择不同物理学科中的几个具体问题,来展示不同形式的高斯及类高斯型积分的应用实例.所选问题的物理内涵及重要性,读者均可从相应的教科书中查阅.
2.1 热力学与统计物理[3]
热力学与统计物理中,在讨论麦克斯韦速度分布律及能量均分定理时,需要计算分子速率的平均及分子速率平方的平均 (见文献[3]中197-200页).为避免重复计算,我们可先得到速率n次方的平均的通用式
(43)
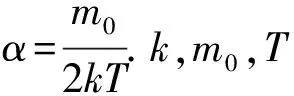

(44)
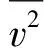
(45)
因此方均根速率为
(46)
2.2 量子力学[1,2,12]
在量子力学中,高斯与类高斯型积分有着广泛应用.

(b) 量子力学中,对同一个问题,可以选择在不同的表象中求解. 一般情况下,解薛定谔方程是在坐标表象中进行的,但对有些问题在动量表象中求解更方便(见文献[12]中卷一108-113页). 一维谐振子既可以在坐标表象也可以在动量表象中精确求解,且在坐标表象中得到的波函数与在动量表象中得到相应的波函数之间可以通过傅立叶变换联系. 以一维谐振子在动量表象中的基态波函数与其在坐标表象中的基态波函数为例
(47)
由于一维谐振子在坐标表象中基态波函数是高斯函数,傅立叶变换时会出现类高斯型积分
(48)
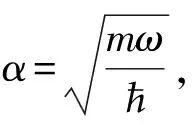
(c) 费曼路径积分作为量子力学(矩阵力学与波动力学之外)的另一种理论形式,其核心是如何计算量子系统的传播子.在费曼路径积分计算自由粒子传播子的过程中,会用到1.5中讨论的类高斯型积分.自由粒子传播子的计算需要计算两个高斯函数乘积的积分(见文献[12]卷二176页),如下

(49)
其中为α、β纯虚数.
3.3 光学[6,11,13]


(50)
分别对比式(50)中等式左边与右边的实部与虚部可得
(51)
(52)
2.4 量子光学[14]

(53)

(54)

(55)
3 小结


