锥形土体模型振动传递特性研究

张家滨， 李潇俊， 唐雪松

(长沙理工大学 土木工程学院， 湖南 长沙 410114)

地铁施工中，盾构机挖掘中会产生振动效应，振动通过土壤、基础、隧道等介质传到地面和地上建筑物，如果产生的振动效应超过许可的振动量级，将影响地上正常的生活和工作，尤其当地铁线路穿过存放精密仪器和高危化工品的高校和化工厂、保管大量贵重文物的博物馆时，如果没有采取合适的防范措施，甚至可能危害到人们的生命和财产安全。经典传递矩阵方法可有效分析土体中振动波的传递过程，给出地下振源与地表振动的关系，但其计算过程较复杂。该文根据地基土的特点，利用锥形土体模型模拟土体振动传递衰减特性，同时引入剪切梁模型计算有限结构土体的固有频率，结合土体波动传递关系和有限结构的固有频率得到土体振动传递特征，分析地下作用荷载下土体的振动衰减规律，评估地下振源对地表结构的影响程度。

1 锥形土体模型

振动在土体中传播的过程中，能量衰减主要包含两个因素：一是能量扩散，土体内振动传递过程中，能量由振源向外辐射，波动面逐渐扩大，单位面积振动能量不断减少；二是振动过程中土体摩擦不断消耗能量。半空间土体柱模型无法描述振动能量扩散问题，有限体采用振型的概念无法描述振动波传递过程中的摩擦阻尼。因此，针对地下隧道施工建立锥形土体模型，通过锥形描述能量的扩散效应，替代有限结构中的振型，评估振动能量衰减效应(见图1)。

隧道施工中，振动能量通过隧道上部传递到土体中，由于隧道深度一般远大于隧道直径，隧道上方土体近似为锥形。锥形杆振动幅值沿深度分布函数表示为：

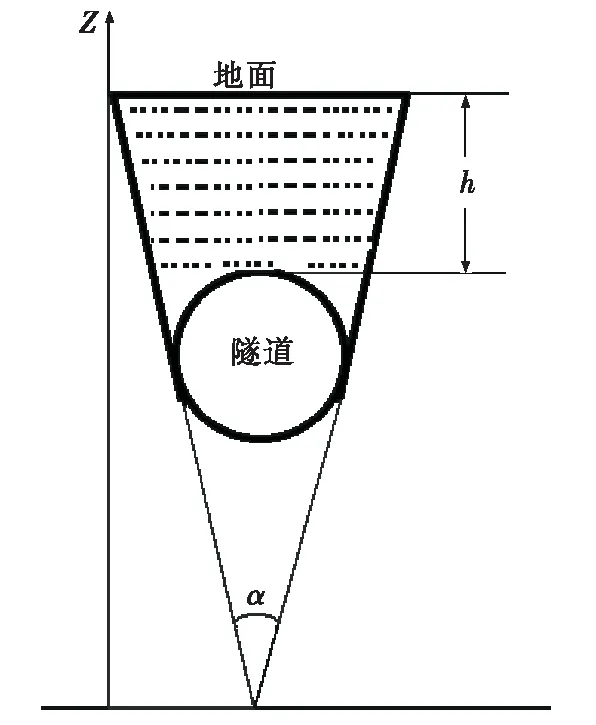
α为辐射角；h为隧道埋深

uz=ekμ*exp(ikz)

(1)

式中：ek为振动扩散效应系数；μ*为黏性阻尼模型；k为波数。

设隧道半径为r，ek和μ*分别为：

(2)

μ*=1+ζi

(3)

利用模态空间求解频域土体动力特性对振源的传递作用，建立隧道上方锥形土体有限元模型，获取有限结构固有频率，边界条件为底部为固支、顶部为自由，分析得到锥形杆纵向固有频率ωr。

从模态域分析，单阶模态振动传递率可表示为固有频率的函数[见式(4)]，传递关系见图2。

(4)

式中：um为模态域中地面振动幅值；ud为隧道顶部振动幅值；λ为激励频率与固有频率的比值，即λ=ω/ωr。

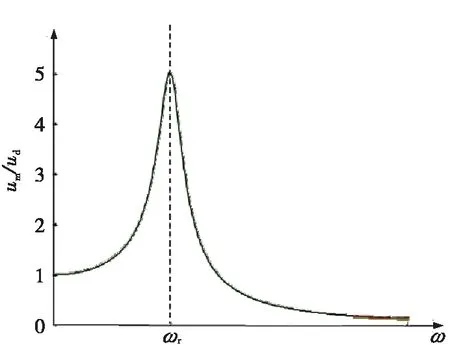
图2 模态传递率

将传递率从模态域转化到物理空间，实际结构振动传递率为：

(5)

式(5)给出了隧道上方土体对不同激励频率的传递特征，同时包含了振动传递过程中的能量扩散效应。

2 土体振动衰减测试对比分析

为对比校验上述理论模型的分析精度，采用长沙地铁6号线地下和地表振动实测数据进行对比分析。长沙地铁6号线烈士公园区间段的地质条件为中风化板岩，隧道埋深22 m，采用圆形隧道结构，土体参数见表1。地下和地表振动测点布置见图3。

表1 岩土材料的物理、力学参数

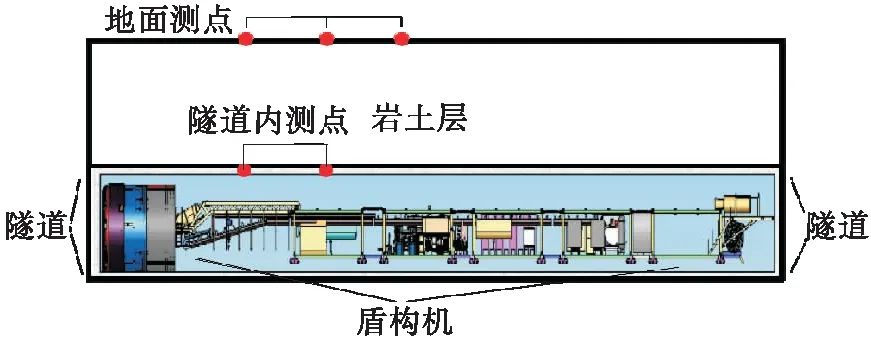
图3 地下和地表振动测试示意图

分别测试隧道顶部和对应地面振动响应，分析振动衰减特征，测试结果见图4。

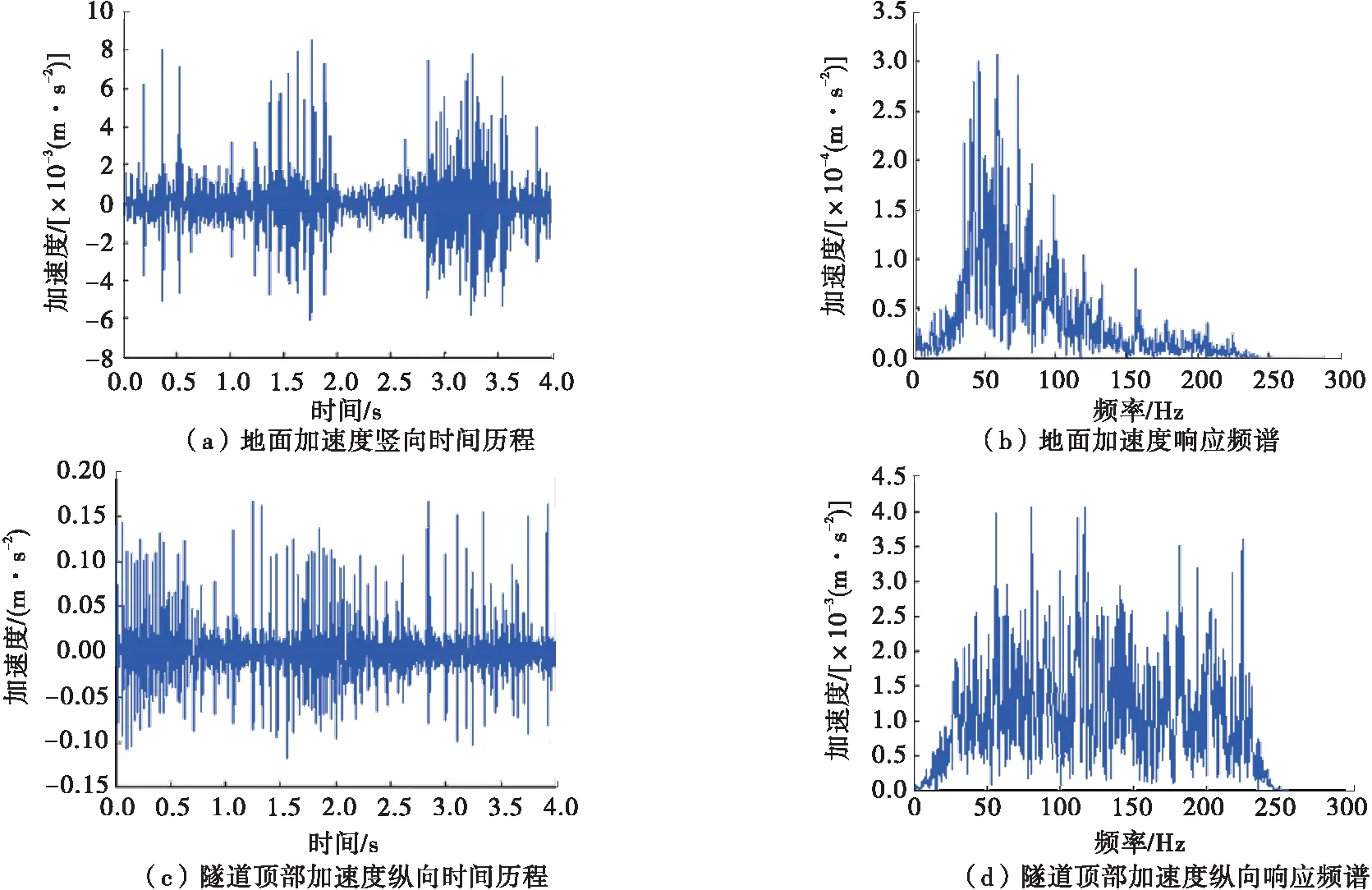
图4 地铁盾构施工振动测试响应数据

施工过程中振动效应竖向占主要成分。从图4(b)来看，地表加速度响应频率变化趋势与图2相同。振动衰减数据取自隧道顶部管片振动响应和地表振动响应，隧道内壁顶部及对应地表最大振动响应见表2。

表2 盾构施工过程中振速对比

利用锥形土体模型计算振动衰减率，辐射角度为15°，阻尼比为0.05，并与实测数据进行对比。结果显示：实测衰减率为79.83%，理论衰减率为76.2%。理论计算所得衰减率与实测数据相近，误差为3.6%，具有较好的参考意义。导致误差的主要原因是岩土结构物理参数复杂、土壤含水率等不确定性较大、模拟过程中理论模型边界条件有所不同、计算过程未考虑隧道结构。

3 结语

利用振动波能量扩散关系替代有限土体结构的振型分布，叠加有限土体的动态响应特性得到地下到地表的振动传递关系，可较为准确地分析土体垂直方向的振动衰减率，评估地铁施工振动效应。

地铁施工振动效应通常针对重点区域，可在进入重点防范区域前测试地下施工过程中的振源、振幅及地表振动幅值、校验辐射角，然后根据传递关系表达式较准确地预估地表振动，为重点保护区域振动预警提供可靠依据。