基于小波网络逆系统的汽油机瞬态空燃比预测控制研究*

杨涛， 宋丹丹

(河南交通职业技术学院 汽车学院， 河南 郑州 450005)

汽油机瞬态空燃比的控制精度是当前发动机控制系统中的难题。瞬态工况下，进气量测量偏差、油膜动态传输特性及氧反馈信号滞后性等导致空燃比控制系统的非线性、时滞性和时变性，传统基于氧传感器的闭环控制很难实现瞬态空燃比精确控制。目前，瞬态空燃比控制研究主要集中在前馈或反馈控制，如利用状态观测器作为前馈控制对缸内进气量进行估计，进而实现空燃比精确控制；文献[5]提出基于神经网络的前馈补偿器，实现对空燃比系统喷油量的补偿。在空燃比反馈控制方面，主要控制方法有PID、模糊控制和预测控制等，如文献[6]设计了基于广义预测控制的空燃比控制策略；文献[7]提出带动态时滞补偿器的模糊PID控制策略，以更好地补偿空燃比系统的时滞和适应系统的非线性。基于前馈加反馈的复合控制策略为瞬态空燃比控制提供了新方向，如文献[9]提出利用自适应混合算法构建发动机空燃比控制器，文献[10]建立了瞬态空燃比的混沌时序LS-SVM预测模型等。为实现瞬态空燃比的有效控制，该文提出基于逆模型前馈控制附加动态矩阵反馈控制的复合控制策略。

1 总体思路

采用逆模型前馈控制附加动态矩阵反馈控制实现空燃比系统的预测控制，空燃比控制系统框图见图1。利用小波网络建立系统逆模型，将其作为前馈控制器对瞬态空燃比系统中进气量进行动态补偿，再将该逆系统与原系统串联，形成伪线性系统，结合动态矩阵控制的预测模型、优化计算和反馈校正对系统的扰动、误差等进行修正，实现对非线性、时滞、时变的瞬态空燃比系统的预测控制。

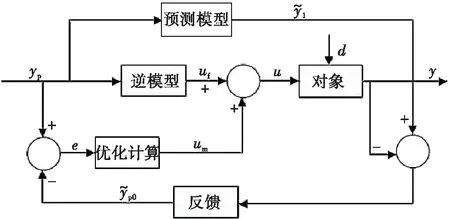
yp为对象期望输出；u、y分别为对象输入、输出；uf为逆系统辨识输出；um为反馈控制优化后输出；d为控制对象的扰动输入；为预测模型输出；为反馈校正输出

2 基于小波网络的逆系统辨识

2.1 瞬态空燃比模型

实际空燃比模型为：

(1)

式中：λ为实际空燃比；ma为每循环进入气缸的空气质量；mf为燃油质量。

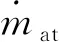
(2)

式中：α为节气门开度；pm为进气管压力。

(3)

式中：ω为发动机转速。

瞬态工况下，进、出气管的空气流速不再相等，则进气管内空气质量流量为:

式中：Vm为进气管容积；R为气体常数；Tm为进气管内温度。

(4)

油膜模型为：

(5)

(6)

(7)

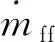
(8)

式中：ti为喷油器喷油脉宽时间(ms)。

综上，空燃比数学模型可表示为：

λ=f(ω,α,ti,pm)

(9)

从上述建模过程可见，发动机瞬态空燃比是一复杂的非线性耦合系统。

2.2 系统逆模型

逆系统控制方法是一种利用直接反馈线性化的解耦控制方法，根据逆系统方法构造的伪线性系统将非线性过程的输入、输出关系近似线性化。

在瞬态空燃比模型中，以喷油脉宽ti作为系统的输入，节气门开度、进气管压力、发动机转速作为系统干扰d，即d=[α,pm,ω]T，空燃比λ为系统输出，瞬态空燃比系统可写为：

f[y(k+α),…,y(k+α-m)n,u(k),…,

u(k-m)]=0

(10)

式中：f(·)为非线性函数；α为输出延迟，α≥1；m为输入阶次；n为输出阶次。

由于喷油脉宽是严格单调的，瞬态空燃比系统的逆模型可写为：

u(k)=g[y(k+α),…,y(k+α-n),u(k-1),

…,u(k-m)]

(11)

2.3 小波网络逆系统的辨识

以小波网络辨识系统逆模型，即用小波网络代替式(11)中的g(·)，根据系统的输出调整网络权值，使小波网络的响应与g(·)相同。

利用下式进行逆模型动态辨识：

(12)

式中：ωj为网络的权值；Dj为伸缩矩阵；aj为平移向量。

基函数采用高斯母小波，其表达式为：

Ψ(t)=(1-t)e-t2/2

(13)

以式(12)代替神经网络的Sigmoid传递函数，用于逆模型动态辨识。图2为逆系统辨识结构图。

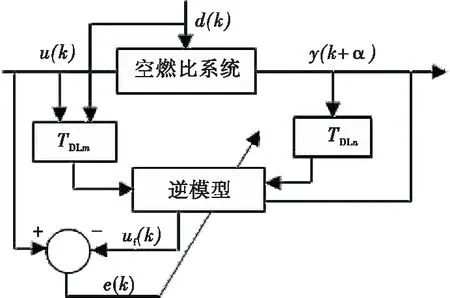
u(k)、y(k+α)分别为系统的输入、输出；TDLm、TDLn分别为输入、输出延时量，TDLm=[u(k-1),…,u(k-m)]，TDLn=[y(k+α-1),…,y(k+α-n)]；uf(k)为逆系统辨识输出；e(k)为辨识输出uf(k)与系统输入u(k)之间的差值，用于训练小波网络

令φ(k)=y(k+α)，则有：

u(k)=g[φ(k),…,φ(k-m),u(k-1),…,

u(k-n)]

(14)

f(g(φ(k)))=f(g(y(k+α)))=y(k)

(15)

即：

(16)

将小波网络逆系统串联在原系统前构成伪线性系统(见图3)，该伪线性系统可实现输入、输出间的线性化。但伪线性系统的开环控制仅消除了非线性特征，不能很好地控制外界扰动、误差等。因此，附加动态矩阵控制这一反馈环节来消除系统干扰。

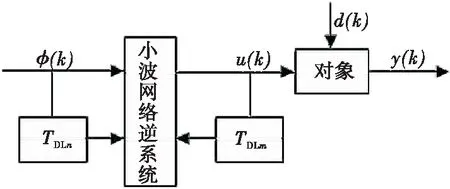
图3 伪线性系统示意图

3 瞬态空燃比的预测控制

采用动态矩阵控制实现预测控制。设控制对象的阶跃响应采样值为{a(1),a(2),…,a(N),…,a(∞)}，N为建模时域，动态矩阵控制时域长度为M，优化时域长度为P，且M≤P≤N，则对象的预测模型可表示为：

YPM(k)=YP0(k)+AΔUM(k)

(17)

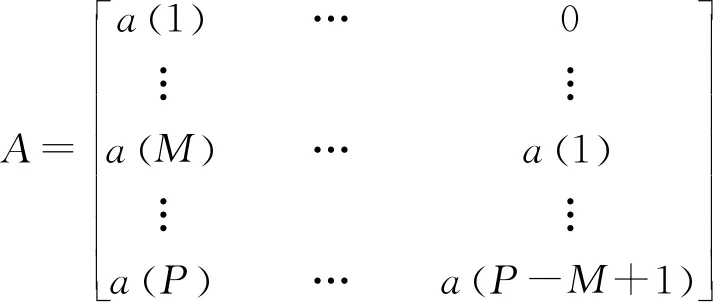
ΔUM(k)=[Δu(k)，Δu(k+1),…,Δu(k+M-1)]

优化性能指标为：

minJ(k)=

(18)

式中：YP(k)=[yp(k+1),…,yp(k+P)]T，为P时刻的期望输出；Q为误差权矩阵[见式(19)]；R为控制权矩阵[见式(20)]。

(19)

(20)

最优控制率为：

ΔUM(k)=(ATQA+R)-1ATQ[YP(k)-YP0(k)]

(21)

一步控制输出为：

Δu(k)=CTΔUM(k)=dT[YP(k)-YP0(k)]

(22)

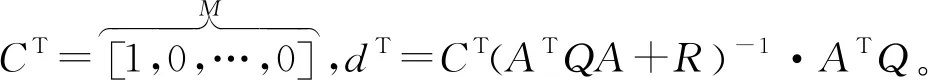
N时刻对象的预测值为：

YN1(k)=YN0(k)+aΔu(k)

(23)

式中：YN0为N时刻初始预测值；a=[a(1)，…，a(N)]T。

预测模型的输出误差为：

(24)

对输出误差加权来修正对未来输出的预测：

YCOR(k+1)=YN1(k)+He(k+1)

(25)

式中：H=[h1,…,hN]T。

得到：

YN0(k+1)=SYCOR(k+1)

(26)

P时刻的初始预测值为：

(27)

4 仿真与分析

4.1 仿真方案设计

(1) 收集试验数据样本来训练小波网络。试验发动机选取HL495Q电喷汽油机，其技术参数见表1。考虑到发动机在瞬态工况的复杂性，同时保证收集的样本数据不失真，试验分阶段进行，分为加速过程和减速过程，分别获取节气门开度、发动机转速、冷却液温度、进气管压力和喷油脉冲宽度等瞬态样本数据，采样时间为0.01 s。加速过程收集节气门由怠速升至85%位置时的数据，共计5×800组；减速过程收集节气门由85%闭合至怠速位置时的数据，共计5×500组。共获得5 200组数据作为训练样本，训练稳定后，采用加速过程800组、减速过程500组数据进行检验测试。获取的样本数据范围见表2，并在训练前对所有数据进行归一化处理。

表1 试验发动机的技术参数

表2 发动机样本数据范围

(2) 利用小波网络对逆模型进行辨识。空燃比控制系统期望输出λ=14.7，输入、输出阶次分别为m=2、n=3，系统延迟α=2。小波基函数采用高斯母小波，网络结构为5-11-2的3层网络。小波网络参数优化采用最速下降法，小波网络的学习和动量因子分别取0.05、0.9。为验证小波网络辨识逆模型的有效性，测试模型瞬态空燃比输出并与台架试验实测值进行对比(见图4)。结果显示，逆模型输出能很好地逼近实际空燃比输出，且反应速度快。

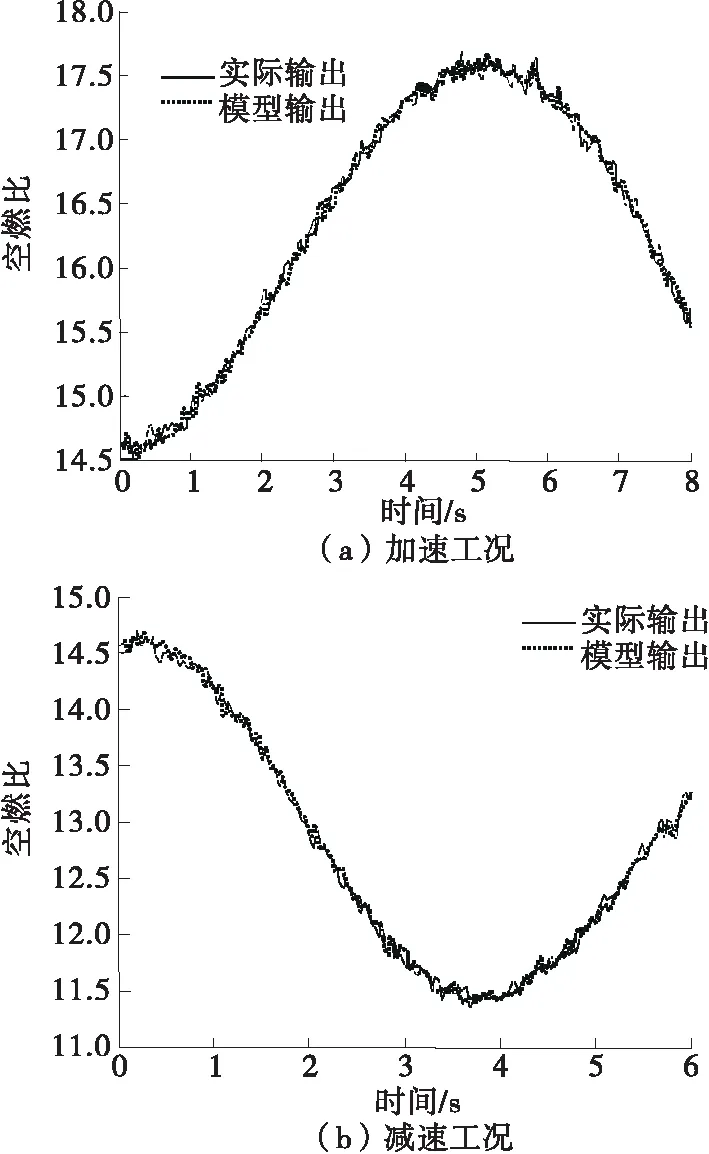
图4 基于逆模型的空燃比输出与实际输出对比

(3) 伪线性系统的验证。将逆模型与空燃比系统结合，对其输入方波信号，输入与输出响应见图5。从中可见，构造的伪线性系统能实现线性化功能，且输入、输出间的时延为2阶。

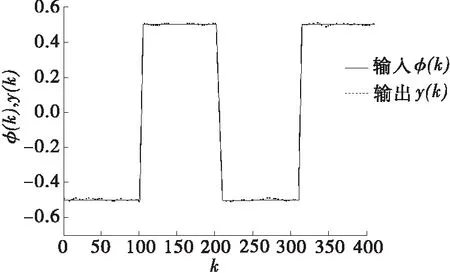
图5 伪线性系统的输入φ(k)与输出y(k)响应

(4) 设计动态矩阵控制器。动态矩阵控制器中的建模时域、预测时域和控制时域分别为N=40、P=15、M=6，误差权矩阵和控制权矩阵分别为Q=0.023Ι(P)、R=0.62Ι(M)。

4.2 仿真结果分析

分别模拟两种瞬态工况对控制策略进行仿真研究，两种工况下节气门变化过程见图6，仿真控制结果见图7。

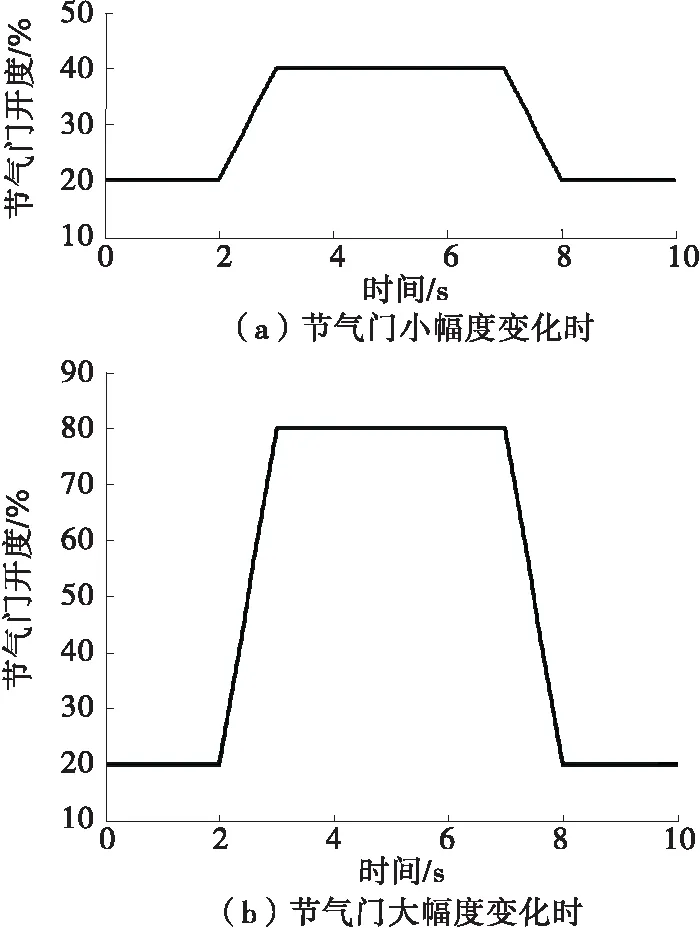
图6 节气门变化曲线

图7 过量空气系数输出

从图6、图7可以看出：当节气门开度变化幅度不大时，系统输出的过量空气系数波动较小，基本维持在期望值1附近，最大失调量约1.01，且响应速度非常快；节气门开度变化幅度较大时，过量空气系数波动较大，但响应速度很快，变化范围在期望值±2.5%内。说明所设计的控制系统具有预测功能，可改善瞬态工况因非线性、系统延时等造成的空燃比大幅变化情况，避免发动机过浓或过稀。

5 结语

为解决瞬态空燃比系统的非线性、时滞等问题，提出一种基于逆模型前馈控制附加动态矩阵反馈控制的复合控制策略，实现空燃比系统的预测控制。仿真结果表明，小波网络辨识的逆模系统具有良好的逼近能力，所构造的伪线性系统能实现线性化功能；前馈附加反馈的复合控制方法能兼顾前馈与反馈的优势，既能高精度逼近空燃比瞬态过程，又可提高系统的鲁棒性和抗干扰能力。基于复合控制策略的预测控制方法可有效控制空燃比系统。