同余数问题的一个新结果*

管训贵

(泰州学院 数理学院，江苏 泰州 225300)

1 引 言

同余数与直角三角形有关，且历史悠久.在公元972年M. B. Alhocain的阿拉伯手稿中就有若干同余数的例子.但是也仅仅是最近50年来，由于Tunnell[1]的工作，我们才对它们有了比较全面的了解.

定义1 一个无平方因子的正整数N称为同余数，如果它是一个有理边长直角三角形的面积，即存在正有理数a,b,c，使得

同余数问题[2]是指：给定一个正整数N，判断它是否是同余数，以及对于一个同余数N，找出面积为N的有理边长直角三角形.

1960年，有三位数学家猜想：所有正整数N≡5,6,7(mod 8)都是同余数.这个猜想至今尚未解决.

目前的主要结果是：

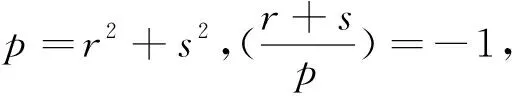
定理B(Monsky，1990) 若素数p≡3(mod 8)，则p不是同余数，但2p是同余数；若素数p≡5(mod 8)，则p是同余数；若素数p≡7(mod 8)，则p和2p都是同余数.

定理C(田野[4]，2014) 任意给定正整数k，在模8余5，6，7的类中有无限多个无平方因子的同余数，这些同余数恰好是k个素因子的乘积.

本文针对N=pq(p,q为不同奇素数)的情形，证明了以下一般性的结果.

定理1 设p,q为奇素数，若下列条件之一成立，则N=pq是同余数：

(ⅰ) 存在正整数r,s,A，使得r4+4s4=pqA2，gcd(r,s)=1，2⫮r.

(ⅱ) 存在正整数r,s,C，使得r4+6r2s2+s4=pqC2，r>s，gcd(r,s)=1，2⫮(r+s).

(ⅲ) 存在正整数r,s,D，使得|r4-6r2s2+s4|=pqD2，r>s，gcd(r,s)=1，2⫮(r+s).

(ⅳ) 存在正整数r,s,A，使得q2r4+4s4=pA2或r4+4q2s4=pA2，gcd(r,s)=gcd(rs,q)=1，2⫮r.

(ⅴ) 存在正整数r,s,A,C，使得r2+4s2=pA2，r2+8s2=qC2，gcd(r,s)=1，2⫮r.

(ⅵ) 存在正整数r,s,D，使得6pr2s2-p2s4-r4=4qD2，gcd(r,s)=1，2⫮rs，p≡1(mod 4)，p⫮r； 或6pr2s2-p2s4-r4=qD2，gcd(r,s)=1，2⫮(r+s)，p⫮r.

(ⅶ) 存在正整数r,s,C，使得r4+6pr2s2+p2s4=4qC2，gcd(r,s)=1，2⫮rs，p≡3(mod 4)，p⫮r；或r4+6pr2s2+p2s4=qC2，gcd(r,s)=1，2⫮(r+s)，p⫮r.

(ⅷ) 存在正整数r,s,D，使得r4-6pr2s2+p2s4=4qD2，gcd(r,s)=1，2⫮rs，p≡1(mod 4)，p⫮r；或r4-6pr2s2+p2s4=qD2，gcd(r,s)=1，2⫮(r+s)，p⫮r.

(ⅸ) 存在正整数r,s,C,D，使得r2+4s2=pC2，r2-4s2=qD2，2⫮r；或4s2+r2=pC2，4s2-r2=qD2，2⫮r.

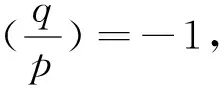
2 关键性引理

引理1N是同余数当且仅当有一个正有理数x，使得x，x+N，x-N都是有理数的平方.

证明参见文献[5].

引理2 不定方程x2+y2=z2满足条件gcd(x,y)=1以及2|x的一切正整数解可表示为

x=2mn，y=m2-n2，z=m2+n2，

这里m,n都是正整数，m>n，gcd(m,n)=1，m,n为一奇一偶.

证明参见文献[6].

引理3 不定方程x2+y2=2z2满足条件gcd(x,y)=1以及x>y的一切正整数解可表示为

x=m2-n2+2mn，y=|m2-n2-2mn|,z=m2+n2,

这里m,n都是正整数，m>n，gcd(m,n)=1，m,n为一奇一偶.

证明由于2|(x2+y2)，gcd(x,y)=1，因此x,y均为奇数.又x>y，因此可设x+y=2a,x-y=2b(a,b是正整数)，此时有x=a+b,y=a-b.由gcd(x,y)=1,知gcd(a,b)=1.把x=a+b,y=a-b代入原方程，得a2+b2=z2.因gcd(a,b)=1，故a,b,z两两互素.于是由引理2，可知

a=2mn,b=m2-n2,z=m2+n2；或a=m2-n2,b=2mn，z=m2+n2.

即

x=m2-n2+2mn,y=|m2-n2-2mn|，z=m2+n2,

这里m>n>0,gcd(m,n)=1,m,n为一奇一偶.引理3得证.

引理4 不定方程x2+2y2=z2满足条件gcd(x,y)=1以及2|y的一切正整数解可表示为

x=|r2-2s2|，y=2rs，z=r2+2s2，

这里r,s是正整数，gcd(r,s)=1，2⫮r.

证明参见文献[6].

引理5 设m为无平方因子正整数,则当m=4k-2时,不定方程x2+my2=z2满足条件gcd(x,y)=1的一切正整数解可表示为

x=|m1r2-2m2s2|,y=2rs,z=m1r2+2m2s2.

这里r,s,m1,m2均为正整数,且gcd(a,b)=gcd(b,m1)=gcd(a,2m2)=1,m=2m1m2.

证明参见文献[6].

引理6 设p为奇素数，则不定方程x2+py2=z2满足条件gcd(x,y)=1的一切正整数解可表示为

这里r,s是正整数，gcd(r,s)=1，r,s都是奇数，p⫮r；或

x=|r2-ps2|，y=2rs，z=r2+ps2,

这里r,s是正整数，gcd(r,s)=1，r,s为一奇一偶，p⫮r.

证明参见文献[6].

3 定理的证明

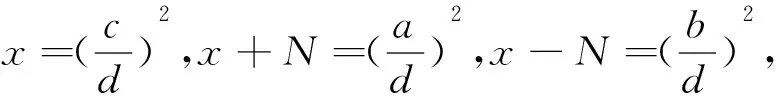
即

a2+b2=2c2，a2-c2=Nd2.

(1)

由(1)的第一式及引理3有

a=|m2-n2-2mn|，b=m2-n2+2mn，c=m2+n2；

(2)

或

a=m2-n2+2mn，b=|m2-n2-2mn|，c=m2+n2.

(3)

这里m>n>0,gcd(m,n)=1,m,n为一奇一偶.

将(2)代入(1)的第二式，整理得Nd2=-4mn(m2-n2)<0，显然不可能.将(3)代入(1)的第二式，整理得Nd2=4mn(m2-n2)，即

(4)

易知，m,n,m+n与m-n两两互素. 假定使式(4)成立的m最小，我们分以下几种情形讨论：

情形1m=pqA2，n=B2，m+n=C2，m-n=D2.

此时有

D2+2B2=C2，pqA2+B2=C2.

(5)

由(5)的第一式及引理4，可得

D=|r2-2s2|，B=2rs，C=r2+2s2，

(6)

这里r,s是正整数，gcd(r,s)=1，2⫮r.

将(6)的后两式代入(5)的第二式并整理得

r4+4s4=pqA2，gcd(r,s)=1，2⫮r.

(7)

由于2⫮r，故2⫮A.对(7)的第一式取模4，有

pq≡1(mod 4).

(8)

情形2m=A2，n=pqB2，m+n=C2，m-n=D2.

则可以找到正整数f和g(必要时可将C替换成-C)，使得

此时有

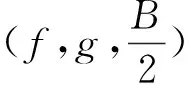
情形3m=A2，n=B2，m+n=pqC2，m-n=D2.

此时有

B2+D2=A2， 2A2-D2=pqC2.

(9)

由于C,D都是奇数，故由(9)的第一式知，A为奇数，B为偶数.根据引理2，(9)的第一式给出

B=2rs，D=r2-s2，A=r2+s2，

(10)

这里r,s都是正整数，r>s，gcd(r,s)=1，r,s为一奇一偶.

将(10)的后两式代入(9)的第二式并整理得

r4+6r2s2+s4=pqC2，r>s，gcd(r,s)=1，2⫮(r+s).

(11)

对(11)的第一式取模8，有

pq≡1(mod 8).

(12)

情形4m=A2，n=B2，m+n=C2，m-n=pqD2.

此时有

A2+B2=C2，A2-B2=pqD2.

(13)

由于C,D都是奇数，A,B为一奇一偶，故由(13)的第一式及引理2知

A=r2-s2，B=2rs，C=r2+s2，

(14)

或

A=2rs，B=r2-s2，C=r2+s2，

(15)

这里r,s都是正整数，r>s，gcd(r,s)=1，r,s为一奇一偶.

将(14)的前两式代入(13)的第二式，整理得

r4-6r2s2+s4=pqD2.

(16)

将(15)的前两式代入(13)的第二式,整理得

6r2s2-r4-s4=pqD2.

(17)

综合(16)、(17)两式可得

|r4-6r2s2+s4|=pqD2，r>s，gcd(r,s)=1，2⫮(r+s).

(18)

对(18)的第一式取模8，有

pq≡1,7(mod 8).

(19)

情形5m=pA2，n=qB2，m+n=C2，m-n=D2.

此时有

D2+2qB2=C2，C2+D2=2pA2.

(20)

根据引理5，(20)的第一式给出

D=|qr2-2s2|，B=2rs，C=qr2+2s2，

(21)

或

D=|r2-2qs2|，B=2rs，C=r2+2qs2.

(22)

将(21)的前后两式代入(20)的第二式，整理得

q2r4+4s4=pA2，gcd(r,s)=gcd(rs,q)=1，2⫮r.

(23)

将(22)的前后两式代入(20)的第二式，整理得

r4+4q2s4=pA2，gcd(r,s)=gcd(rs,q)=1，2⫮r.

(24)

(25)

情形6m=pA2，n=B2，m+n=qC2，m-n=D2.

此时有

B2+D2=pA2，2B2+D2=qC2.

(26)

由于D为奇数，m,n为一奇一偶，故由(26)的第一式知B为偶数、A为奇数.

令D=r,B=2s，则(26)的两式给出

r2+4s2=pA2，r2+8s2=qC2，gcd(r,s)=1，2⫮r.

(27)

又C也为奇数，故对(26)的两式分别取模8可得p≡1(mod 4)，q≡1(mod 8).注意到p,q可交换，就必有

(p,q)≡(1,1),(5,1),(1,5) (mod 8).

(28)

情形7m=pA2，n=B2，m+n=C2，m-n=qD2.

此时有

B2+pA2=C2，C2-2B2=qD2，pA2-B2=qD2.

(29)

根据引理6，(29)的第一式给出

(30)

这里r,s是正整数，gcd(r,s)=1，r,s都是奇数，p⫮r；或

B=|r2-ps2|，A=2rs，C=r2+ps2，

(31)

这里r,s是正整数，gcd(r,s)=1，r,s为一奇一偶，p⫮r.

将(30)的前后两式代入(29)的第二式，整理得

6pr2s2-p2s4-r4=4qD2，gcd(r,s)=1，2⫮rs，p⫮r.

(32)

对(32)的第一式取模8，有6p-2≡4q(mod 8)，得p≡1(mod 4).

将(30)的前后两式代入(29)的第二式，整理得

6pr2s2-p2s4-r4=qD2，gcd(r,s)=1，2⫮(r+s),p⫮r.

(33)

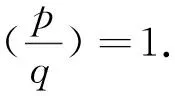
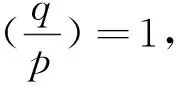
(34)

情形8m=A2，n=pB2，m+n=qC2，m-n=D2.

此时有

D2+pB2=A2，2A2-D2=qC2，A2+pB2=qC2.

(35)

根据引理6，(35)的第一式给出

(36)

这里r,s是正整数，gcd(r,s)=1，r,s都是奇数，p⫮r；或

D=|r2-ps2|，B=2rs，A=r2+ps2，

(37)

这里r,s是正整数，gcd(r,s)=1，r,s为一奇一偶，p⫮r.

将(36)的前后两式代入(35)的第二式，整理得

r4+6pr2s2+p2s4=4qC2，gcd(r,s)=1，2⫮rs，p⫮r.

(38)

对(38)的第一式取模8，有6p+2≡4q(mod 8)，得p≡3(mod 4).

将(37)的前后两式代入(35)的第二式，整理得

r4+6pr2s2+p2s4=qC2，gcd(r,s)=1，2⫮(r+s),p⫮r.

(39)

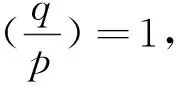
(40)

情形9m=A2，n=pB2，m+n=C2，m-n=qD2.

此时有

A2+pB2=C2，2A2-C2=qD2，A2-pB2=qD2.

(41)

类似于情形8的讨论知，存在正整数r,s，使得

r4-6pr2s2+p2s4=4qD2，gcd(r,s)=1，2⫮rs,p≡1(mod 4),p⫮r;

(42)

或

r4-6pr2s2+p2s4=qD2，gcd(r,s)=1，2⫮(r+s),p⫮r.

(43)

并且有

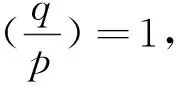
(44)

情形10m=A2，n=B2，m+n=pC2，m-n=qD2.

此时有

A2+B2=pC2，A2-B2=qD2，pC2+qD2=2A2.

(45)

由于C为奇数，m,n为一奇一偶，故由(45)的第一式知，A,B为一奇一偶.

当A为奇数，B为偶数时，令A=r,B=2s，则(45)的前两式给出

r2+4s2=pC2，r2-4s2=qD2，2⫮r.

(46)

当A为偶数，B为奇数时，令A=2s,B=r，则(45)的前两式给出

4s2+r2=pC2，4s2-r2=qD2，2⫮r.

(47)

(p,q)≡(1,1),(1,7),(5,5),(5,3)(mod 8).

(48)

由式(7)，(11)，(18)，(23)，(24)，(27)，(32)，(33)，(38)，(39)，(42)，(43)，(46)和(47)可得定理1.

由式(8)，(12)，(19)，(25)，(28)，(34)，(40)，(44)和(48) 可得定理2.

4 若干例子

例1 试证：N=5×13=65是同余数.

证明在定理1(i)中取r=1,s=2可得pq=5×13，A=1.此时m=65,n=16.代入式(3)得a=6049，b=1889，c=4481，从而由(1)的第二式得d=504.故

根据引理1知，N=65是同余数.又因为

例2 试证：N=17×89=1513是同余数.

证明在定理1(ii)中取r=6,s=1可得pq=17×89，C=1.此时m=1369,n=144.代入式(3)得a=2247697，b=1459153，c=1894897，从而由(1)的第二式得d=31080.故

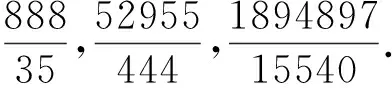
例3 试证：N=7×17=119是同余数.

证明在定理1(iii)中取r=3,s=2可得pq=7×17，D=1.此时m=144,n=25.代入式(3)得a=27311，b=12911，c=21361，从而由(1)的第二式得d=1560.故

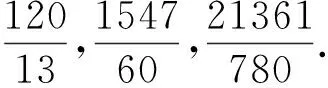
例4 试证：N=73×3=219是同余数.

证明在定理1(iv)中取r=1,s=2,q=3可得p=73，A=1.此时m=73，n=48，代入式(3)得a=10033，b=3983，c=7633，从而由(1)的第二式得d=440.故

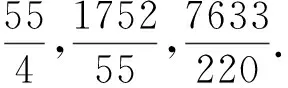
例5 试证：N=13×17=221是同余数.

证明在定理1(v)中取r=3,s=1可得p=13,q=17，A=C=1.此时m=13,n=4，代入式(3)得a=257，b=49，c=185，从而由(1)的第二式得d=12.故

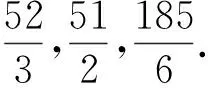
例6 试证：N=5×41=205是同余数.

证明在定理1(vi)中取r=3,s=1,p=5可得q=41，D=1.此时m=45，n=4，代入式(3)得a=2369，b=1649，c=2041，从而由(1)的第二式得d=84.故

例7 试证：N=3×7=21是同余数.

证明在定理1(vii)中取r=s=1,p=3可得q=7，C=1.此时m=4,n=3，代入式(3)得a=31，b=17，c=25，从而由(1)的第二式得d=4.故

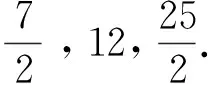
例8 试证：N=13×23=299是同余数.

证明在定理1(viii)中取r=s=1,p=13可得q=23，D=1.此时m=36,n=13，代入式(3)得a=2063，b=191，c=1465，从而由(1)的第二式得d=84.故

例9 试证：N=53×5=265是同余数.

证明在定理1(viii)中取r=7,s=1可得p=53,q=5，C=1,D=3.此时m=49，n=4，代入式(3)得a=2777，b=1993，c=2417，从而由(1)的第二式得d=84.故