求解二维矩形件装箱问题的布谷鸟算法*

冯文健

(柳州铁道职业技术学院， 广西 柳州 545616)

0 引言

二维矩形装箱问题(2D rectangular strip packing problem, 2DRSPP)是将一组长度、宽度不等的矩形互不重叠的装入给定宽度、长度不限的矩形条带箱中，使得箱子被矩形占用的高度最小。该类问题是NP难问题，在工业领域被广泛应用，因此对此类问题的求解有重要的研究价值。目前对2DRSPP的研究主要集中于算法设计，可分为精确算法、启发式算法和混合智能算法，由于精确算法求解时间较长，只适合较小规模算例。而后两者成为求解2DRSPP的主流算法[1-4]。近年来，相关学者提出一些更有效的启发式算法和混合智能算法，尚正阳等[5]设计一种启发式最优剩余空间算法，提出求解二维矩形装箱问题的启发式算法；邓见凯等[6]提出一种求解二维矩形Packing问题的拟人型全局优化算法；罗强等[7]提出求解矩形件排样问题的十进制狼群算法；江林燕[8]提出基于化学反应优化算法的装箱问题研究；车玉馨[9]提出装箱问题的启发式算法研究；高东琛[10]提出二维装箱问题的启发式算法。

本文设计了算法1并结合布谷鸟算法求解二维矩形装箱问题，通过多组测试算例的仿真实验，结果表明本文设计的算法对部分测试算例效果较好，对部分测试算例效果较差。

1 二维矩形装箱问题描述

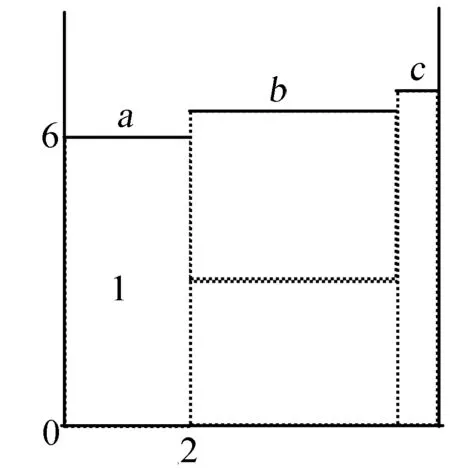
图1 矩形件装箱示意图

假设第i个小矩形pi的长度和宽度分别表示为wi和hi，排放在宽度为W、高度不限的大矩形带箱strip上，矩形件i排放后左上角的横坐标、纵坐标和宽度分别为xi、yi和wi。排放的过程中矩形件之间不重叠、矩形件不超出strip的边界和矩形件底边与strip边平行3个约束条件。H为n个矩形件排放完后的最大高度，Y为矩形件面积之和与排样最大高度之下的面积比。为了便于对2DRSPP进行数学描述，以左下角0为坐标原点建立如图1所示的二维坐标系，每一个item用左上角的横坐标、纵坐标和宽度来表示，比如矩形1则表示为(0,6,2)，4个item放置strip中形成3条水平线(图中a,b,c所示)，2DRSPP的目标如下：

(1)

s.t.∀pi:0≤xi≤W,0≤xi+wi≤W,yi≥0

(2)

∀pi,pj:xi≤xj≤xi+wi

(3)

∀pi,pj:yi≤yj≤yi+wi

(4)

其中式(3)和(4)保证所有矩形件互不重叠和不超出strip的边界，本文研究的2DRSPP是矩形件不可旋转。

2 算法描述

应用智能算法求解2DRSPP的关键点在于编码和解码，本文采用浮点数编码方式，然后对其排序得到十进制整数，每一个整数即为矩形件的唯一标识；解码即运用算法对有序的整数序列转化为排样图。

2.1 算法1

算法1过程描述如下：

(1)初始化最低水平线及strip的宽度；

(2)按面积从大到小排序，得到排序序号集set；

在选购机械设备的过程中，要将效益放在首要位置，争取企业的效益能够实现最大化，选择设备时需要按照经济实惠的原则。

(3)如果集合set不为空；循环执行步骤4～6；

(4)统计所有未放入strip中的矩形newdata；

(5)判断newdata中是否存在能够放入strip中的矩形；

(6)如果存在，则将矩形放入strip中，求解新的水平线并删除宽度为0的水平线，再判断最低水平线是否可以合并，如果可以则合并最低水平线并更新最低水平线，然后从集合set中删除相应的矩形；如果不存在，则将此时最低水平线提升至与其相邻矩形中最低高度齐平，然后合并最低水平线宽度。

(7)直至集合set为空退出循环，输出最大高度。

2.2 布谷鸟算法

布谷鸟算法(cuckoo search algorithm，CS)是YANG Xin-she和DEB Suash于2009年提出[11]，该算法结构简单、容易实现，其全局搜索过程依靠Levy飞行选择鸟巢，其迭代式如下：

(5)

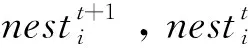
局部搜索过程则以一定概率pa抛弃鸟巢和新建鸟巢。

(6)

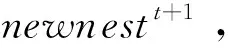
2.3 策略1

由于在弃巢过程中未利用群体的最佳位置，可能会导致收敛速度和精度不高，因此将式(6)改为下式：

(7)

其中，r1,r2∈[0,1]之间的随机数，m1，m2，m3表示n个不重复的随机整数。

2.4 策略2

为了增强局部搜索能力，对当前鸟巢执行轮盘赌选择(参见遗传算法)、交叉(随机选择两个鸟巢和随机选择两个位置进行交叉)和逆序(随机选择两个位置进行倒序)操作。

2.5 改进布谷鸟算法

改进布谷鸟算法(improved cuckoo search algorithm，ICS)求解过程如下：

(1)初始化种群数目、最大迭代次数、弃巢率和边界等参数。

(2)在边界范围内随机初始化种群并降序排列，按算法1求解目标值(高度)，求解当前种群最优值(最小高度)及最优解。

(3)开始循环迭代，按式(5)获得新鸟巢然后评估最优值及最优解，若较之前的优越则替换；按式(7)建立新鸟巢并重新评估最优值及最优解，若较之前的优越则替换。

(4)执行N=5次数策略2并重新评估最优值及最优解，若较之前的优越则替换。

(5)判断循环是否结束，如果是输出最优值及最优解，对最优解降序排列得到的序列即为矩形件的排样顺序，否则跳转至步骤(3)。

3 仿真实验

为了验证ICS的性能，本文实验1数据来源于文献[12]，实验2的数据来源于http://people.brunel.ac.uk/～mastjjb/jeb/info.html；所有实验基于windows平台使用matlab语言编写实现，硬件环境为i7-9750H 2.60GHz CPU,8G内存。算法的参数设置：种群规模为20，弃巢率为0.25，交叉率为0.85，最大迭代次数为100。

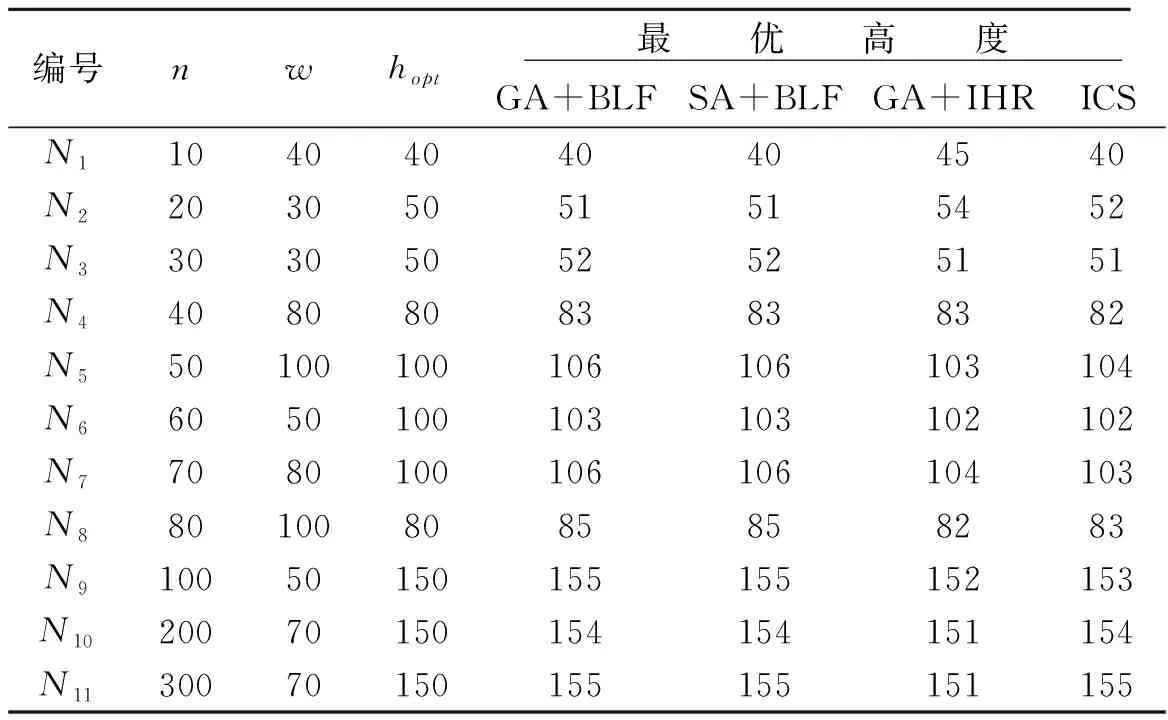
表1 算例N的比较结果

3.1 实验1

实验1采用经典的N算例对本文算法进行测试，并与GA+BLF，SA+BLF，GA+IHR算法进行比较，统计结果见表1，排样效果如图2、图3所示。表1中的n，w，hopt分别表示矩形个数、strip宽度和已知最优高度。

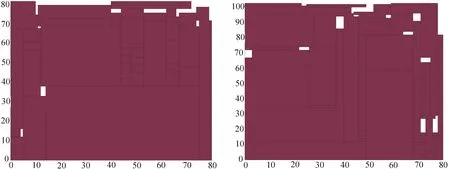
图2 N4排样图 图3 N7排样图

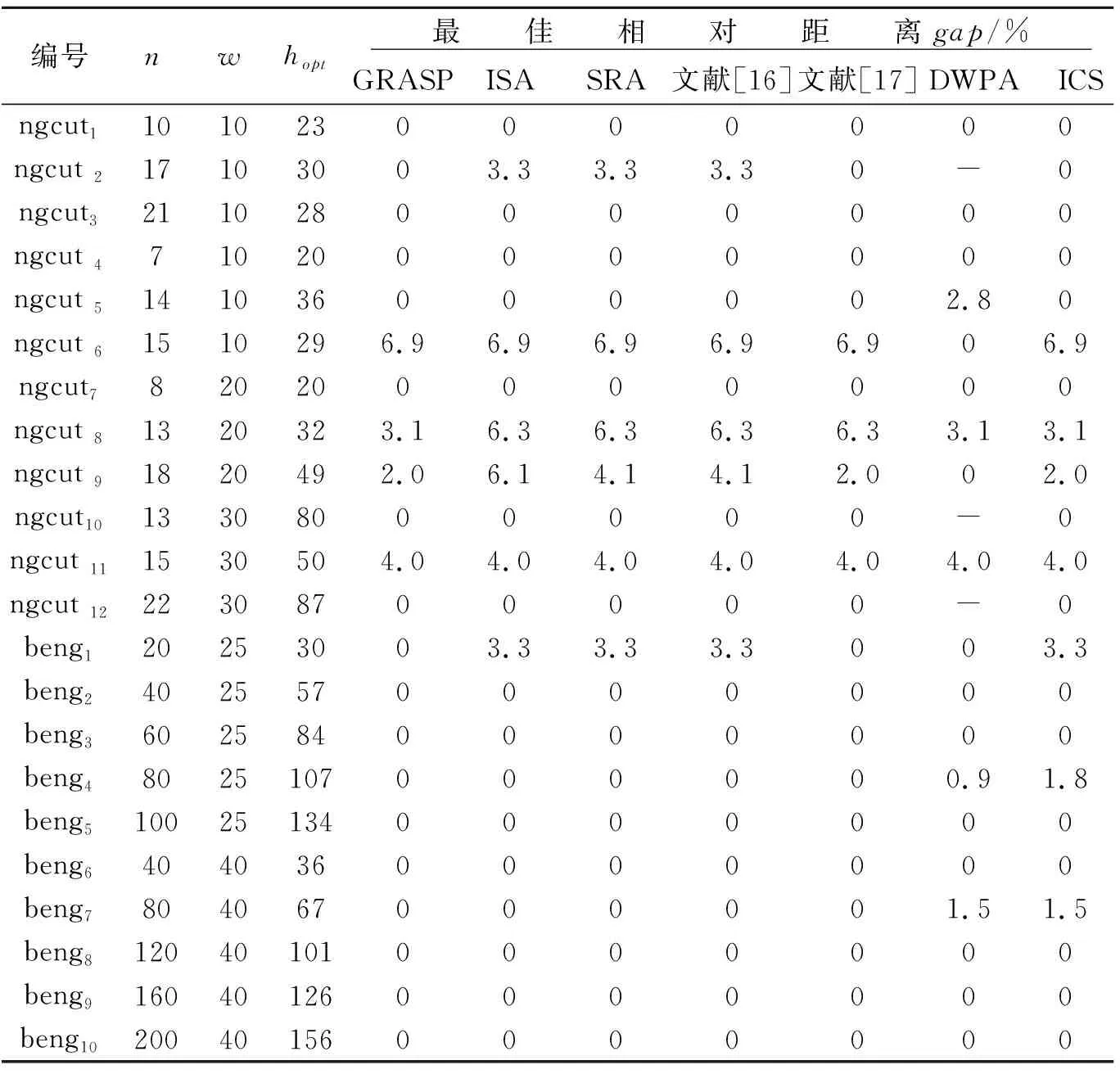
表2 ngcut和beng算例的统计结果

从表2可知，本文算法在N4、N6和N7算例上求解的最优值均优于GA+BLF、SA+BLF和GA+IHR算法；本文算法在N3～N9算例上求解的最优值均优于GA+BLF和SA+BLF算法，在N10,11算例上求解的最优值与其一致，仅在N2算例上求解的最优值较其差；与GA+IHR算法相比，求解结果优于的有算例N1、N2、N4和N7；求解结果一致的有N3和N6；求解结果较差的有算例N5、N8、N9、N10和N11。通过11个N类算例验证了本文的有效性。

3.2 实验2

实验2的ngcut算例共有12个子算例，均属于小规模问题。beng算例共有10个子算例。矩形为20～200个。采用相对距离来评价计算结果，gap=(h*-hopt)/hopt×100 ，h*表示计算的最优值，hopt为已知最优值，gap越小表示算法越好。并与文献[13～17]、DWPA算法进行比较，统计结果见表2，部分排样效果如图4、图5所示。表2中的n，w，hopt分别表示矩形个数、strip宽度和已知最优高度。

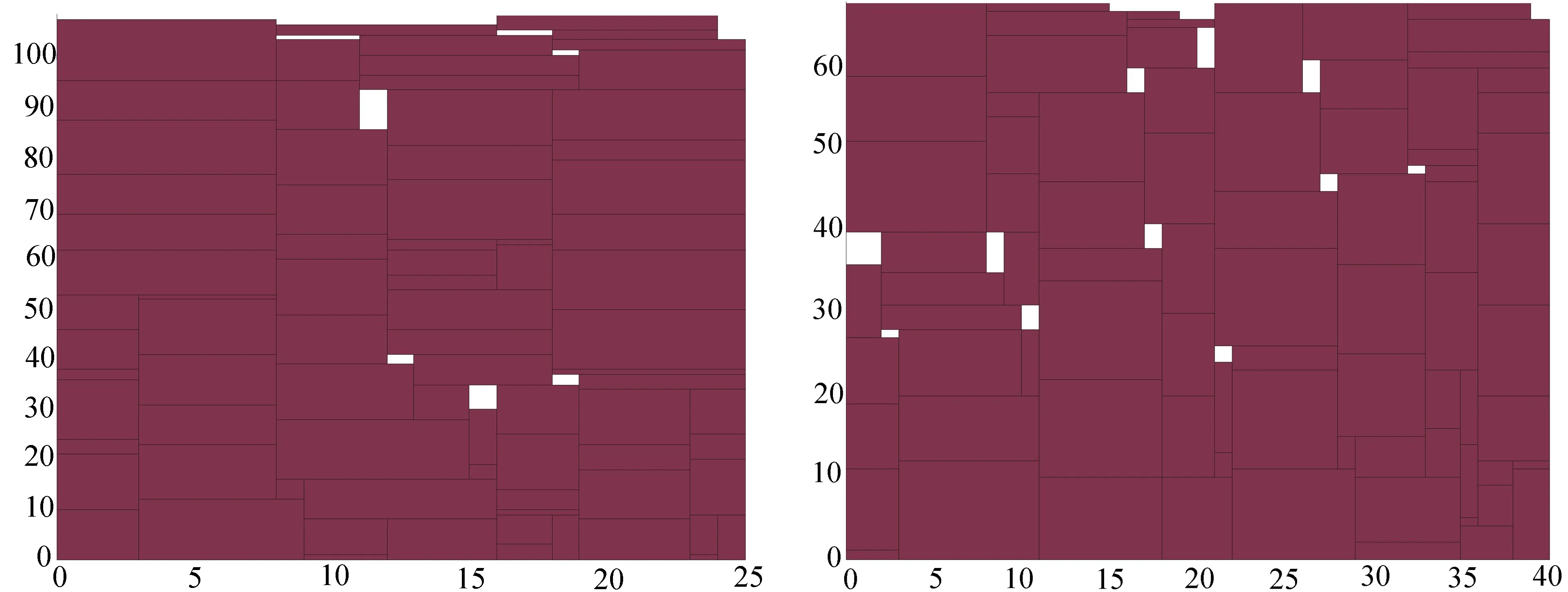
图4 beng4排样图 图5 beng7排样图

从表2可知，对ngcut小规模的测试算例，本文的求解效果与GRASP效果一致，优于ISA、SRA、文献[16]、文献[17]算法，差于DWPA算法，但对ngcut 5算例，本文和其他算法均优于DWPA算法。对于beng测试算例，本文的求解效果差于其他算法。因此，从所有的测试算例来看，本文设计的算法对N类和ngcut类装箱问题求解效果较好，但对beng类装箱问题求解效果差于其他算法。

4 结 语

本文在布谷鸟算法基础之上设计算法1，并改进局部搜索迭代公式，同时为增强局部勘探能力，对鸟巢进行轮盘赌选择、交叉和逆序操作，采用浮点数编码方式求解二维矩形装箱问题，应用多组测试算例对算法进行仿真实验，并与其他智能算法进行比较，结果表明对N类和ngcut类装箱问题求解效果较好，但对beng类装箱问题求解效果较差，如何进一步提高装箱效果是下一步研究方向。