Tavis-Cummings模型的几何相位特性研究
舒鹏丽,高 平,王燕锋
(吕梁学院 物理系,山西 离石 033001)
0 引言
1984年,M.V.Berry[1]在研究绝热循环系统的含时哈密顿量时,发现了一个不同于动力学相位的额外相因子,称之为绝热几何相位[2]。Berry指出在绝热近似条件下,体系的瞬时本征态经周期循环演化,得到的几何相位不依赖于体系的动力学性质[3],而是与具体演化路径的几何结构有关,是不可积的相位因子,随后,实验上[4,5]也证实了该几何相位的存在。自从Berry提出几何相位的概念以来,几何相位的研究引起了很多研究者的关注,得到了一系列的发展[6,7,8],并广泛应用各种量子体系,如单个二能级原子与单模光场的相互作用系统(Jaynes-Cummings模型[9,10])、两二能级原子与单模光场相互作用系统(Tavis-Cummings模型[9,11])等量子系统。
本文选取Tavis-Cummings模型为研究对象,在体系的某一瞬时绝热本征态下计算几何相位,得到几何相位随系统参数的演化关系,这为利用几何相位实现量子逻辑门[12]容错操作提供一定的理论基础。
1 物理模型
Tavis-Cummings模型中两原子间存在偶极相互作用的系统哈密顿量可表示为:
(1)
(2)
(3)

为研究方便,将(1)式转化到相互作用绘景中,则T-C模型的哈密顿量表示为:
(4)
以希尔伯特空间中的|e1,e2,n〉,|e1,g2,n+1〉,|e2,g1,n+1〉和|g1,g2,n+2〉作为基矢,考虑系统共振情况,即ω≈ω0,(4)式可写为矩阵形式:
(5)
根据(5)式,可求得四个非简并的本征能量Ej和其相应的本征态|φj〉(j=1,2,3,4),将每个绝热瞬时本征态以希尔伯特空间的基矢展开:
|φj〉=cj1|e1,e2,n〉+cj2|e1,g2,n+1〉+cj3|g1,e2,n+1〉+cj4|g1,g2,n+2〉
(6)
其中|cj1|2+|cj2|2+|cj3|2+|cj4|2=1.
为计算几何相位,绝热瞬时本征态(6)变换到薛定谔绘景中,引入时间演化算符:
U(t)=U(φ)=exp[-iφ(t)a+a],
(7)
其中φ(t)周期性变化,变化范围为[0,2π]得到:
|φj(t)〉=U(t)|φj〉=U(φ)|φj〉,
(8)
系统的几何相位计算式[13]为:
(9)
将(7)、(8)代入(9)式得到:
γj=2π[n|cj1|2+(n+1)(|cj2|2+|cj3|2)+(n+2)|cj4|2].
(10)
2 数值模拟
2.1 几何相位与原子与光场间相互作用的演化
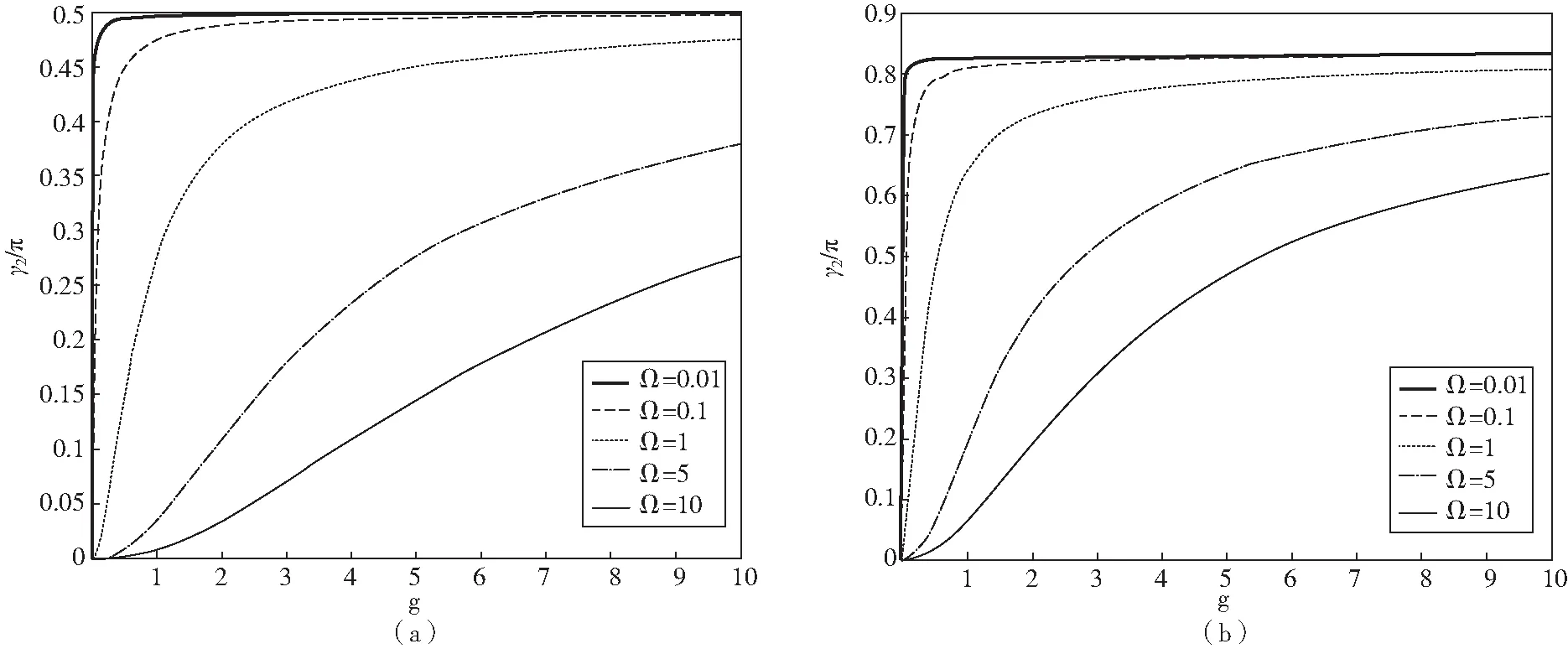
图1 几何相位随原子与光场间相互作用的演化
从图1(a)可以看出,当偶极间耦合系数Ω比较小时,几何相位γ2随原子与光场间的相互作用强度g从零迅速变为0.5π,随后保持该值不变,当Ω比较大时,γ2随g逐渐增大,在给定g下,随着Ω的增大,γ2的值减小,即γ2的增长曲线越来越平缓,但最终都趋于一稳定值0.5π。可以判断当系统光子数为n=0,偶极间的作用Ω可以忽略时,γ2几乎不受g变化的影响,保持稳定值0.5π。当Ω不可以忽略时,其取值可减缓γ2随g变化的增速,并随Ω取值的增大,对γ2的减缓效果越明显,但γ2仍随g的增大而增大,且趋于稳定值0.5π。
取光子数n=6,偶极间耦合系数取值Ω=0.01,0.1,1,5,10时,研究γ2随原子与光场间相互作用强度g的演化。如图1(b),两者间的演化关系与图1(a)相似,两图的不同点在于,当光子数n=6时,γ2最终趋于的稳定值为0.826π,说明几何相位的取值不仅取决于原子与光场间的相互作用,还取决于光子数的大小,光子数越多,几何相位越大。
2.2 几何相位与偶极-偶极间耦合系数的演化
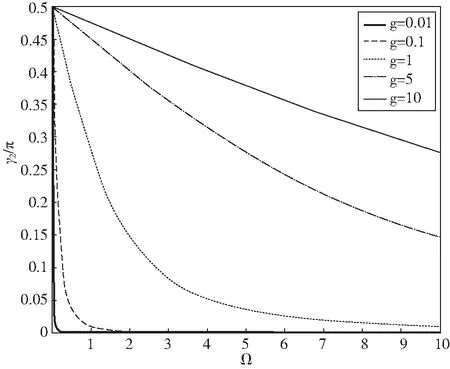
图2 几何相位与偶极-偶极间耦合系数的演化
令原子与光场间相互作用系数取值g=0.01,0.1,1,5,10,光子数n=0,讨论γ2随偶极-偶极间耦合系数的演化关系。图2中,当g比较小时,γ2随Ω从0.5π迅速降为零,并维持零相位不变,当g较大时,γ2随Ω从0.5π逐渐减小,在给定Ω下,随着g的增大,γ2的值增大,即γ2的下降曲线越来越平缓,最终趋于零相位,表明几何相位随偶极间耦合系数呈下降趋势,但原子与光场间的相互作用可减缓该下降趋势。取光子数n=6,几何相位γ2随Ω从0.826π下降并趋于零相位。经对比,当光子数取值相同时,几何相位随原子与光场相互作用增长的起点(终点)和几何相位随偶极间耦合系数下降的终点(起点)相同,这直接表明了几何相位与光子数的取值相关。下面来研究几何相位与光子数的变化关系。
2.3 几何相位与系统光子数的演化
图3(a)中Ω/g取值分别为10,100,500,1 000,观察到几何相位γ2随光子数n从零开始增大,当n达到107数量级时,γ2趋于π。另外,在不同的Ω/g取值下,γ2的增长速度随Ω/g的增大逐渐放缓,即在给定n下,Ω/g值越大,γ2越小,但最终随着n增加趋于一稳定值π。从前面讨论已知,γ2随Ω的增大而减少,说明γ2随n的增长速度明显大于随Ω的减少速度,从而整体表现为增长趋势。
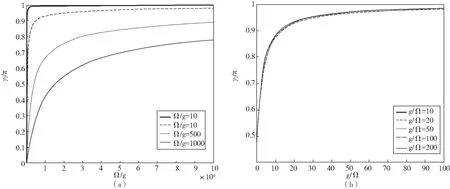
图3 几何相位与系统光子数的演化
图3(b)中g/Ω的取值分别为10,20,50,100,200,此时几何相位γ2随光子数从0.5π开始增大,当光子数的数量级在102时,γ2就趋于π,随着g/Ω变大,几何相位的变化曲线间的差别越来越小,g/Ω越大,曲线越趋于重合。可以推断,g≫Ω,即Ω可忽略时,γ2的取值主要由n决定,受g变化的影响较小,该结论正好与图1吻合。
3 结论
从上面的讨论可以推出,几何相位随原子-光场间相互作用的增大而增大,随偶极-偶极间耦合系数的增大而减少,随光子数的增大而增大,但都不是无限地增大或减少,几何相位最终都趋于一稳定值,该稳定值由光子数的取值而确定,当光子数为0时,几何相位稳定值为0.5π,光子数比较大时,稳定值为π,几何相位稳定值变化范围γ2∈[0.5π,π],表明几何相位随不含时参数的演化,与原相位相差模为1的因子。
同样可选取本征能量E3对应的本征态作为绝热本征态计算几何相位,得到几何相位随偶极间的耦合系数的增大而增大,随原子-光场间相互作用系数的增大而减少,随光子数的增大而增大,总体来讲,这几个参数的相互博弈影响几何相位的取值。当选取E1和E4对应的本征态时,几何相位仅与光子数有关,呈线性增长关系,可见在同一哈密顿量下选取不同的绝热本征态,可得到几何相位不同的演化情况,这为实现不同的量子逻辑门操纵提供了可能。

