基于差分法的水波动画模拟

杨 艳，范示示，王艳永

(吕梁学院 数学系，山西 离石 033001)

水波动画的模拟主要分为三类[1]：第一类是基于波的分析方法，其中最简单的一种是用正弦函数来进行仿真，模拟水波表面.这种方法只是从形态上模拟了水波的特性，并没有考虑水波在运动过程中外部与内部环境以及其他现实因素的影响.第二类是基于粒子的分析，将流体看作是离散的粒子集，每个粒子按照一定的规则不断的运动.第三类是基于物理模型的方法，研究流体的运动，最典型的是通过求解粘性不可压缩流体的动量守恒方程：Navier-stokes方程，得到流体完整的速度场.

本文采用二维水波方程，设定水滴落下的初值条件，得到方程的差分解，并且通过稳定性讨论，得到参数的取值范围，模拟水面荡漾动画.

1 模型的建立

本文选用二维水波方程[2]：

(1)

(1)式中z表示水面高度，x,y为空间变量，t为时间变量，其中c、μ均是非负的常数，c表示单位时间内水波位移的距离，μ表示流体的黏度.

由于在模拟水滴湖面波动的过程中，波面是从滴落位置(x0,y0)开始呈直径为w的圆环扩散的，在垂直方向的最大位移为h.为了能够产生水滴湖面造成的湖面的波动这一状态，先获取湖面下落的初始圆环的高度h和宽度w，设定:

(2)

为方程的初始条件，表示圆环内部曲面向下凹陷，同时圆环外水面的垂直位移都为零，如图1.

图1 初始条件图像

同时初值条件包括:

(3)

边界条件选取

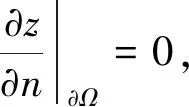
(4)

2 差分法求解模型

将区间[a,b]和[c,d]分别n等分，步长分别为Δx,Δy(为了讨论方便，取方形区域，此时记相同步长为Δd)，得到空间结点(xi,yj)(0≤i≤n,0≤j≤n).令Δt为时间步长，并用z(xi,yj,tk)表示tk时刻点(xi,yj)的水面高度.

2.1 方程的离散

将方程(1)中各个导数用如下二阶格式离散，

(5)

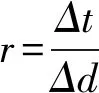
(6)

代入(5)式整理，得方程的差分解为:

(7)

2.2 初始条件的离散

将

舍去误差项，代入初始条件(3)，得:

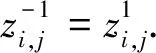
(8)

(7)式中取k=0，得：

将(8)式代入整理，得:

(9)

综合(7)式和(9)式，得方程的差分解为:

(10)

3 解的稳定性分析

黏性阻尼力μ为与温度有关的量，可以通过经验得到，数量级为10-3.为了讨论稳定性，需确定波速c和Δt的关系.

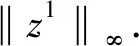
故

(11)

由(6)式，得a2>0,a3<0(由于μ为10-3，Δt取充分小，即假设μΔt≤2)，故：

此时，(11)式可写为：

假设a1>0，即：

(12)

又由于a2>0，上式可写为：

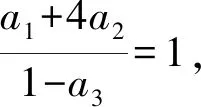
同理，k=0,1,2,…时，由(7)式可得：

(13)

故有：

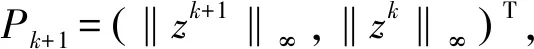
记，

要使(13)式稳定，需矩阵A的谱半径ρ(A)≤1+C0Δt,其中C0为常数.

进一步计算A的特征值为：

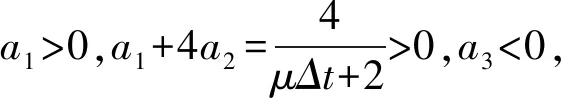
以下证明存在常数C0，使得ρ(A)≤1+C0Δt，即存在常数C0，使

用反证法，假设对于认识常数C0，都有

成立，按C0降幂整理得：

Δt2(μΔt+2)2C02+2μΔt2(μΔt+2)C0+2μ2Δt2-8<0，

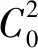
4 模拟结果

图3 波面荡漾开画面

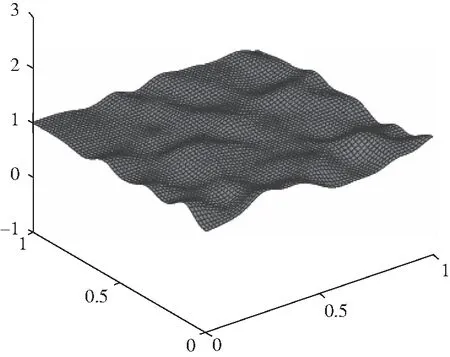
图4 整个水域波动

图5 水面趋于平静

以上四幅图是随着时间增加，水面的各个不同时间运动图，从水滴反弹到波面趋于平静的状态.

5 结束语

通过有限差分法求解二维的水波方程，模拟了随机的水滴滴落从而引起湖面波动的动画.讨论了满足稳定条件的参数取值范围，并分析了初值和边界值的选取.结果表明，该方法可以真实的模拟水滴湖面波动的现象.本文是作为本科生的数值分析课程的扩展实验项目.在文献[2][3]中均有类似讨论，创新点是从数学角度对稳定的条件进行推导.下一步工作类似于文献[2][3]，可以结合计算机图形学课程光照模型，使得动画具有真实感，提高学生实验能力.