基于二型模糊大脑情感学习控制器的双足机器人容错控制研究

叶荣冠， 郑飞杰

( 1.三明学院 机电工程学院，福建 三明 365004;2.肇庆学院 机械与汽车工程学院，广东 肇庆 526061 )

0 引言

目前，双足机器人已被广泛应用于军事、搜索、救援等多个领域.但由于机器人不可避免地会出现一些无法预知的故障，因此需要一种自动容错的控制方案来实时监测和估计机器人系统的故障[1-2].目前，已有一些学者对此进行了研究.例如：文献[3]通过引入一种鲁棒自适应死区的方法来识别机器人系统中发生的故障，并通过重新配置控制律来防止系统在出现故障时发生跟踪性能恶化；然而这种自适应死区技术无法对建模进行不确定性补偿，因此控制性能仍需提高.文献[4-6]使用学习方法因应网络、电子设备及机器人控制过程中出现的故障，但该方法在系统发生大非线性变化故障时其控制性能仍存在不足.研究显示，二型模糊集具有良好的处理系统不确定性的能力[7-11]，大脑情感学习控制器具有较快的学习能力[12-16]；因此，本文将二型模糊集与大脑情感学习控制器(type-2 fuzzy brain emotional learning controller,T2FBELC)相结合，利用二型模糊大脑情感学习控制器对机器人系统进行控制，并通过实验验证了本文方法的可靠性.

1 双足机器人动力学模型

双足机器人的结构示意图如图1所示，该结构系统在非线性故障下的动力学方程为[2]：

(1)

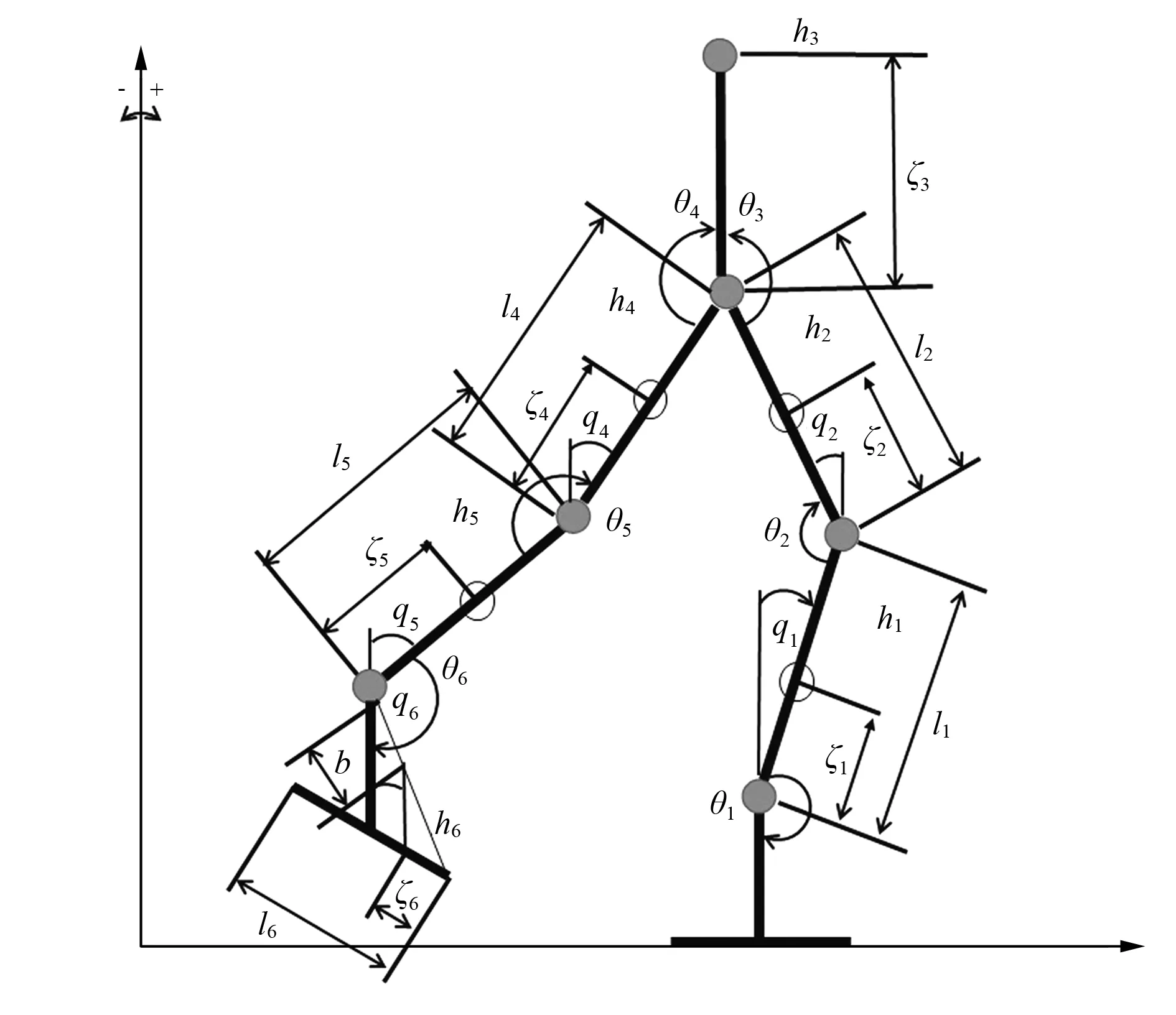
图1 双足机器人结构示意图

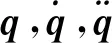
M(q)={δτ1τ2cos(qτ1-qτ2)},

τ1=1,2,…,6,τ2=1,2,…,6.

(2)

式(2)中δτ1τ2是双足机器人因应运动变化的瞬时参数，各参数如表1所示.表1中hτ1是双足机器人的质量，lτ1是双足机器人的长度，miτ1是双足机器人的转动惯量，b(b=0.12)是双足机器人的增益.双足机器人连杆的质量和长度如表2所示.

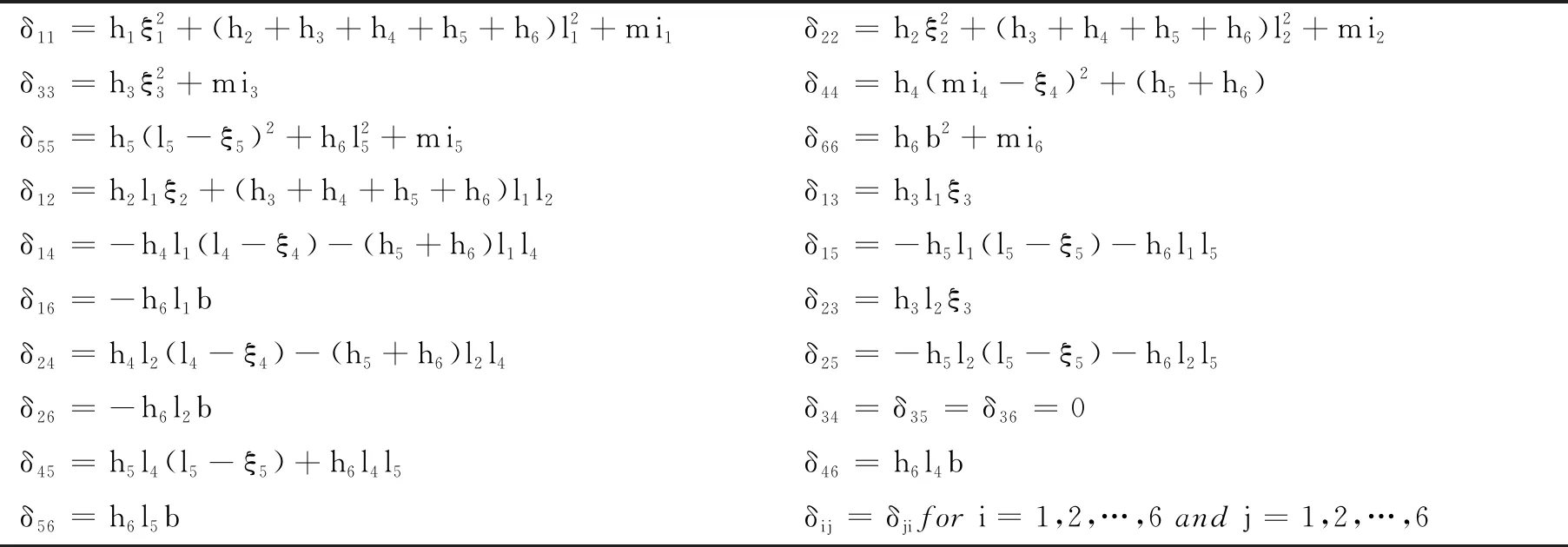
表1 双足机器人因应运动变化的瞬时参数

式(1)中，向心力矩阵C∈R6×6和重力矩阵g∈R6的表达式为：

(3)

双足机器人各连杆耦合的重力参数βτ1如表3所示.表3中r代表重力加速度，为9.81 m/s2.假设双足机器人动力学故障的未知矢量为：

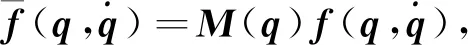
(4)

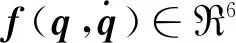
(5)

表2 双足机器人连杆的质量和长度

表3 双足机器人的重力参数

2 控制器与非线性估计模块

2.1 控制器

图2 基于T2FBELC的双足机器人反馈控制系统的结构

基于二型模糊大脑情感学习控制器的机器人反馈控制系统的结构如图2所示.双足机器人的控制器主要由计算转矩控制器和鲁棒控制器组成.计算转矩控制器的作用是稳定控制系统，其工作方式是根据机器人反馈的现况信息与期望位置、速度的误差量来计算控制输入量；鲁棒控制器的作用是通过二型模糊大脑情感学习控制器估计系统故障变化的值，并通过实时调整来实现容错控制的目的.

在没有系统故障的情况下，式(5)可表示成如下的动力学方程式：

(6)

由双足机器人的动力学模型及控制系统架构可知计算转矩控制器输出u0的方程为：

(7)

式中：qd为期望的轨迹矢量，qd∈R6；e(e=qd-q)为关节位置矢量的跟踪误差，e∈R6;K1和K2为对角反馈增益矩阵，K1,K2∈R6×6.将式(7)代入式(6)可得误差动态方程式为：

(8)

在式(8)中，通过选择适当的K1和K2即可使跟踪误差达到稳定的收敛，进而可获得计算转矩控制器的输出值u0，此时控制器的输入值u=u0.

2.2 非线性估计模块

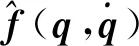
(9)

3 二型模糊大脑情感学习控制器

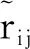
(10)

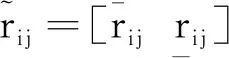
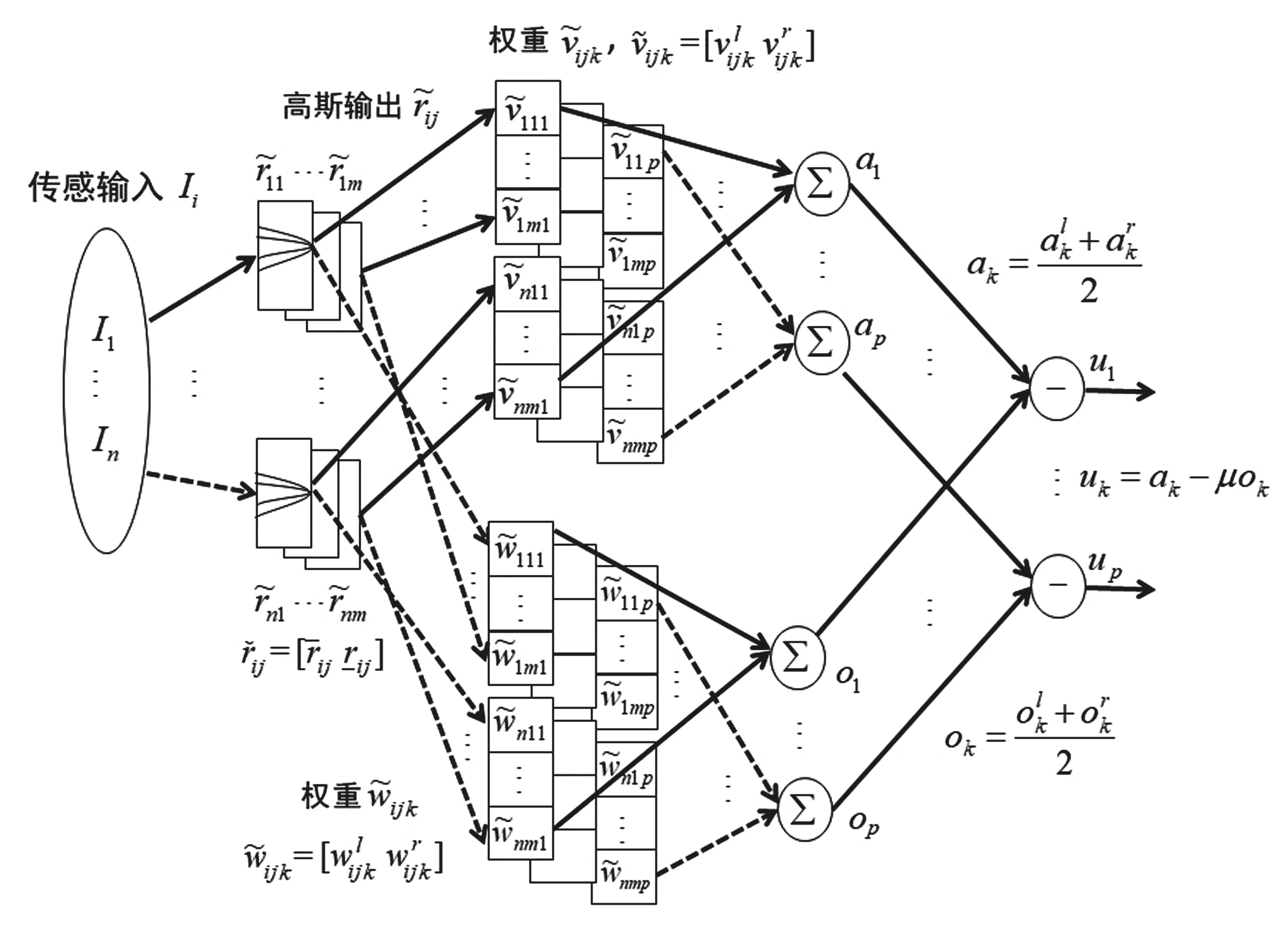
图3 二型模糊大脑情感学习控制器的示意图

在图3中，感觉神经的模糊杏仁核网络的表达式为：

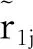
其中ak是杏仁核网络的输出量，p是状态变数的输出数量.

在图3中，情感神经的模糊眶额皮质网络的表达式为：

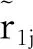
其中ok是眶额皮质网络的输出量.

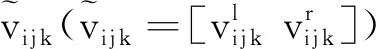
fori=1,2,…,n,j=1,2,…,m,k=1,2,…,p.

fori=1,2,…,n,j=1,2,…,m,k=1,2,…,p.

因此杏仁核网络输出的左、右点值可以表示为：

4 仿真实验

案例1考虑一个由一系列复杂因素造成的双足机器人的非线性故障.假设故障发生在连杆1和连杆2中，且故障发生在第2.5 s，此时故障的函数表达式为：

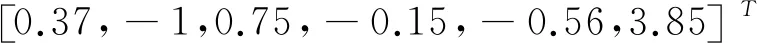
案例2为了验证控制器的鲁棒性和容错控制能力，对双足机器人进行系统不确定性仿真，即在案例1发生故障的情形下，在第3.5 s时增加系统的未知项变化量和外部扰动.未知项变化量与外部扰动函数分别用如下方程表示：

(11)

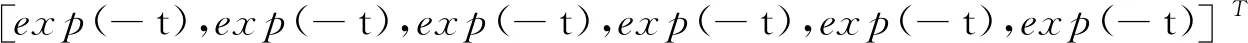
(12)

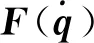
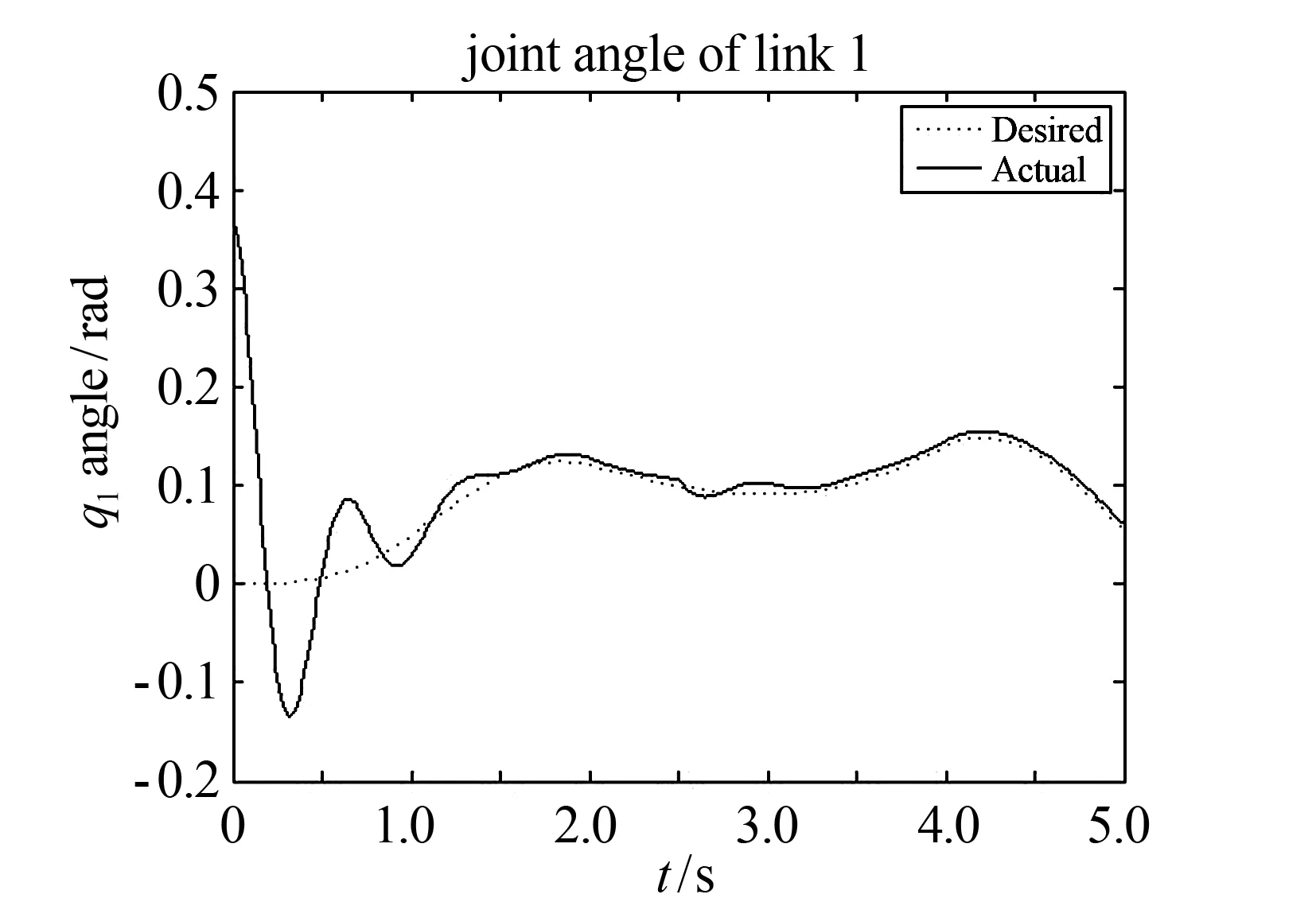
图4 双足机器人发生非线性故障时各连杆关节角的跟踪时间位置(案例1)

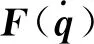
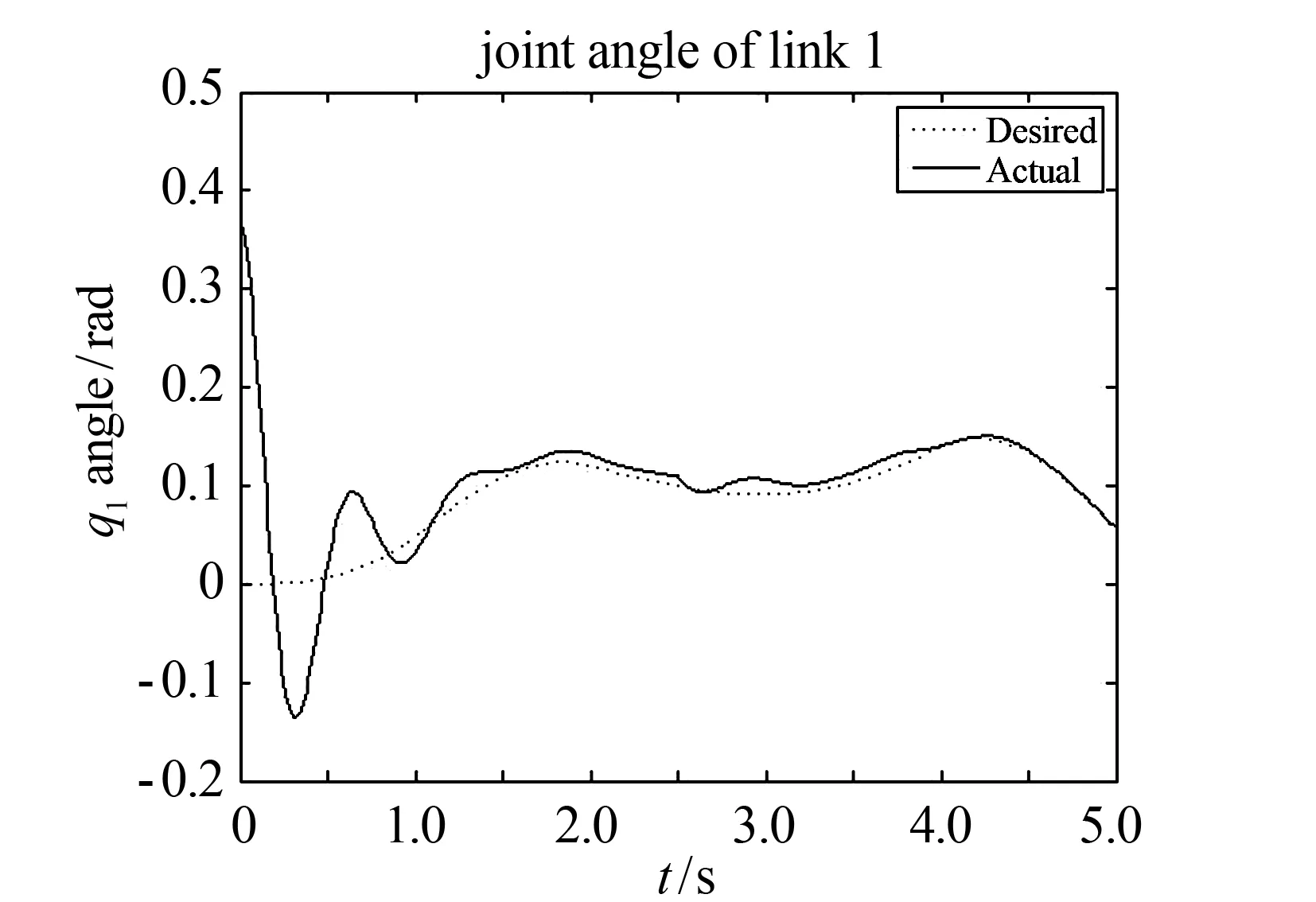
图5 双足机器人受到外部扰动时各连杆关节角的跟踪时间位置(案例2)

5 结论

利用本文提出的二型模糊大脑情感学习控制器对双足机器人进行行走控制表明，该方法具有良好的跟踪误差收敛性和容错能力，因此该方法可提高双足机器人行走控制的可靠性，并可为其他类型移动机器人的容错控制提供参考.在今后的研究中，我们将对双臂双足机器人的运动数学模型及其基于T2FBELC的容错控制做进一步的研究.