基于RBF-BP神经网络融合的医学数据分类研究

金丹丹， 闻辉

( 1.莆田学院 护理学院,福建 莆田 351100;2.莆田学院 信息工程学院,福建 莆田 351100 )

0 引言

目前，神经网络已经被广泛应用于医学诊断过程中，其中反向传播(BP)神经网络和径向基函数(RBF)神经网络是医学诊断过程中最为常用的两种网络模型.BP神经网络的隐节点核函数一般采用统一的sigmoid核对输入样本进行映射，该方法虽然具有良好的泛化性能，但存在收敛速度慢和容易陷入局部最小的缺点.目前优化BP神经网络的方法主要有基于全局优化的初始化权值[1]、自适应调整学习速率[2]、增加动量项[3]、修正误差代价函数[4]以及动态调整网络结构[5]等,这些方法虽然在一定程度上改善了BP神经网络的不足，但对于较复杂的非线性问题其效果仍十分有限.RBF网络隐节点核函数一般采用高斯核对输入样本进行映射，具有良好的局部响应特性.RBF网络的优化过程主要包括隐层核参数的优化以及线性输出权值的优化,其实现过程可以分为两个阶段：一是先将原始样本通过隐层高斯核的映射，以此改善样本的可分性；二是通过优化线性超平面来完成模式分类.目前优化RBF神经网络典型的方法有k-均值聚类[6]、模糊c均值聚类[7-8]、敏感度分析[9]、势函数优化[10]等，但这些方法在优化复杂的非线性问题时，往往会加大RBF网络线性输出权值优化的负担，进而影响网络的性能.为此，本文针对医学诊断数据集的特点(样本量少、特征复杂)，提出了一种将RBF神经网络与BP神经网络相融合的HRBF-BP算法,并利用UCI机器学习数据库[11]中的3个基准医学诊断数据集(Heart Disease、Diabetes、Breast Cancer)验证了本文算法的有效性.

1 HRBF-BP网络模型的构建

HRBF-BP模型的构建原理为：首先将原始样本输入到RBF隐层中不同参数下高斯核函数的映射中，以此提取原始样本在不同空间区域中的局部特征，从而形成新的特征向量；然后利用RBF隐层所级联的BP网络来完成特征空间中样本的有效分类.相对于BP网络，HRBF-BP改善了输入样本的可分性，因此可以加快网络的权值收敛速度，减少陷入局部最小的风险；相对于RBF网络，HRBF-BP将原有连接RBF网络隐层与输出层的线性权值连接更改为非线性的BP网络，因此其对复杂问题具有更强的适应能力.因此，HRBF-BP可以将RBF网络隐节点处的局部非线性映射能力与BP网络的全局非线性分类能力有效地结合起来，从而有效改善单一结构RBF神经网络及BP神经网络的不足.

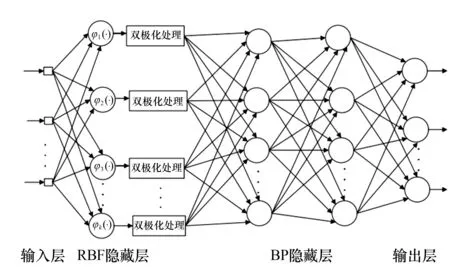
图1 HRBF-BP网络模型图

图1为本文所构建的HRBF-BP神经网络模型.该模型由输入层、RBF隐藏层、BP隐藏层以及输出层4个部分组成，其中RBF隐藏层由一组不同参数的高斯核函数组成.设RBF隐藏层中高斯核的个数为K，当输入的样本为x时，通过隐藏层的高斯核的映射可表示为：

j=1,2,…,K.

(1)

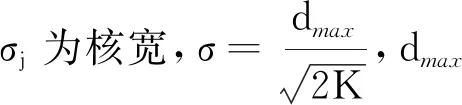
gj(x)=2·φj(x)-1.

(2)

在HRBF-BP网络中，BP隐藏层由RBF隐层到RBF输出层之间的各层节点组成.由于BP隐藏层的sigmoid函数为双曲正切函数，因此第l个BP隐藏层中的节点j的输出信号可表示为:

(3)

其中a和b为常数.

2 HRBF-BP网络算法的实现

图2 HRBF-BP网络学习算法

HRBF-BP网络算法的实现分为两个阶段：一是优化RBF网络隐节点处各高斯核的参数，二是优化BP网络中各层的权值.图2为HRBF-BP网络算法的具体实现过程.图2中，BP网络的整体均方误差的计算公式为：

其中dj为HRBF-BP网络的目标输出，oj为网络的实际输出，c为输出节点的个数.

BP网络的反向计算即为局域梯度的更新过程，可表示为：

BP网络中第l层权值的更新过程为

其中m为迭代步长，η为学习率.

3 实验与分析

为了验证本文算法的性能，利用UCI机器学习数据库中的3个不同的医学数据(见表1)对本文算法、SGBP算法、KMRBF算法、PFRBF算法的性能进行实验对比.实验中：各数据样本全部归一化到[-1,1]；RBF隐藏层中的核个数根据样本空间的分布进行调整(手动)；分别设定BP隐层的层数为1层和2层，隐藏层节点的个数设置为2～9，网络学习率η采用模拟退火算法进行迭代调整，sigmoid核参数取a=1.716，b=0.667.实验运行环境为Intel(R) Core(TM) i5-7500，3.4 GHZ CPU，8 G RAM，MATLAB 2013，每个实验重复10次.

表1 不同分类数据集的信息

表1中，HD数据集用于诊断303个患者是否患有心脏病.Diabetes数据集用于诊断患者是否患有糖尿病，BC数据集用于诊断患者是否患有乳腺癌.

3.1 基准医学分类数据集下不同算法的性能对比

在基准医学数据集下，本文算法与其他算法的性能对比结果见表2—表4.由表2—表4可以看出：本文算法在学习过程中虽然比KMRBF和PFRBF算法略增加了一些训练时间，但其训练精度和测试精度均优于其他算法，这表明本文算法对训练样本空间具有更好的学习效果.另外，由表2—表4还可以看出，在本文算法中2个BP隐藏层数所需的训练时间明显少于1个BP隐藏层数所需的训练时间，且训练精度和测试精度也得到进一步提高.

表2 HD医学数据集下不同算法的性能

表3 Diabetes医学数据集下不同算法的性能

表4 BC医学数据集下不同算法的性能

3.2 参数分析

图3 RBF隐藏层节点个数变化时HRBF-BP与KMRBF算法的分类性能

以Diabetes医学数据集为例进行参数分析.首先固定BP隐藏层层数和BP隐层节点个数，然后通过调节RBF隐层节点个数来对比HRBF-BP网络和KMRBF算法的性能，结果如图3所示.由图3可以看出，当RBF隐层节点个数为16～30，RBF隐层节点个数为14～30时，其所对应的KMRBF算法和HRBF-BP算法的网络分类精度虽均可维持在一个稳定的精度范围内，但HRBF-BP的网络分类精度显著优于KMRBF算法.该结果进一步表明,HRBF-BP网络比KMRBF算法具有更好的学习能力.

在Diabetes医学数据集中，不同的RBF隐层节点个数、BP隐藏层层数以及BP隐层节点个数对HRBF-BP算法性能的影响见表5.由表5可以看出，HRBF-BP算法的训练精度和测试精度相对较为稳定，且均优于KMRBF算法.这表明，HRBF-BP算法能够有效降低对参数(RBF隐层节点个数、BP隐藏层层数以及BP隐层节点个数)选择的依赖.

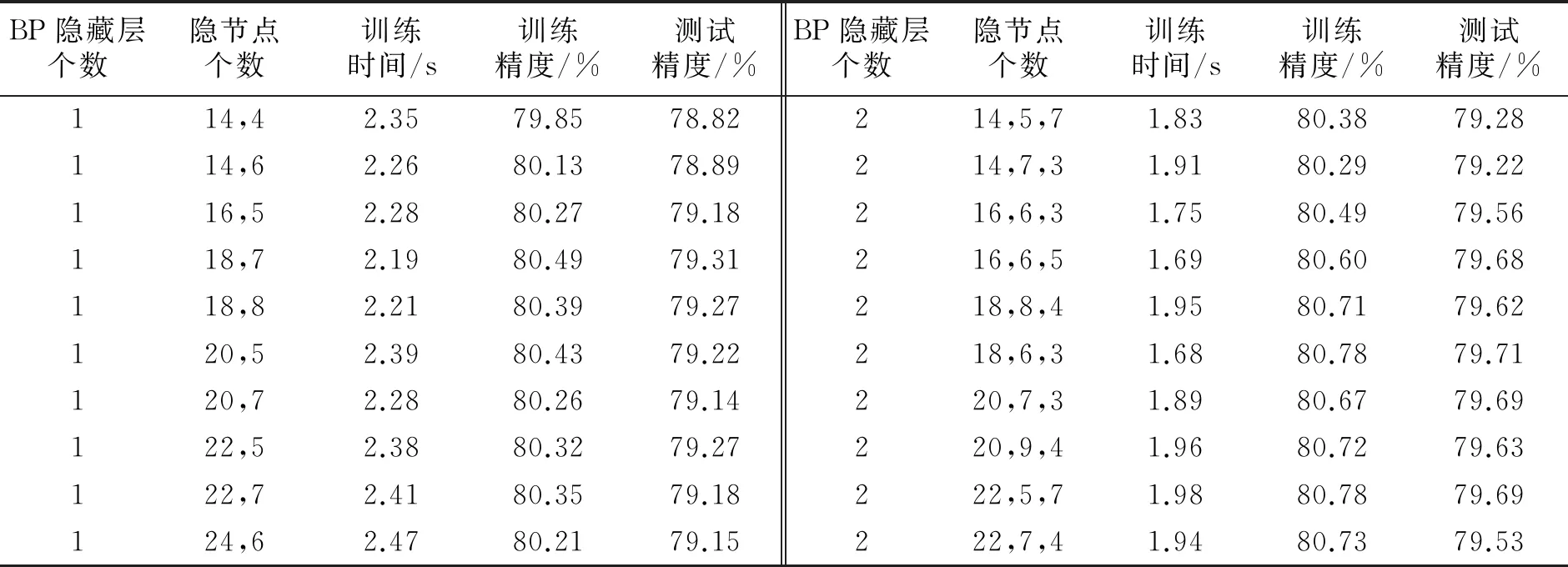
表5 不同参数下HRBF-BP算法的性能

4 结论

研究表明，本文提出的HRBF-BP算法可将RBF网络稳定性好与BP网络泛化能力强的优点融合在一起，且其训练精度和分类精度均优于SGBP、KMRBF、PFRBF算法；因此，本文算法可有效改善单一RBF网络及BP网络的分类性能和提高网络学习的性能.在研究中，本文的训练样本采用的是批学习方式，未能考虑序列样本的学习方式，因此在今后的研究中我们将引入基于序列样本的HRBF-BP算法，以完善本文算法.