跨声速轴流涡轮特性预估方法

杜玉锋，高杰，郑群，马国骏

哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001

0 引 言

我国舰船技术高速发展，作战系统和控制系统愈发成熟[1]。涡轮发动机作为现阶段的动力核心，高负荷单级涡轮是发展重点，其可减轻涡轮部件质量，提高推质比[2-3]。单级高负荷涡轮中动叶或静叶易产生激波，故针对跨声速涡轮，需一套行之有效的判断临界界面及性能预估的方法。

Stodola 最早提出对单级涡轮的效率和流量进行预测的经验关系式[4]。Bammert 等[5]在其基础上通过实验提出必须逐级计算多级涡轮的性能。对于损失模型，Soderberg[6]给出了动叶以及静叶中的能量损失估算方程公式和气流转折角的损失。Ainley 等[7]通过叶栅实验矫正了损失模型，提出了轴流涡轮的特性预估方法，为涡轮特性预估的发展打下了基础。Dunham 等[8]在文献[7]的基础上，考虑了马赫数对叶型损失的影响，并通过试验修改了经验公式。

针对跨声速涡轮，Denton[9-11]研究了跨声速涡轮的内部损失机理，将尾缘损失从叶型损失中独立出来，不仅方便计算，也提高了计算准确度。同时，在计算公式中加入跨声速涡轮的激波损失公式，使涡轮的特性预估更准确。近几年，Tournier 等[12]分析了各种损失模型，Baturin 等[13-14]分析了轴流涡轮由于叶型所产生的损失，对实验数据与计算值偏差进行统计分析，提出了一种评估轴流式涡轮叶栅能量损失模型的可靠方法。

在发动机技术方面，国内取得的进展较慢，多以仿制为主。燃油机研制亦沿袭前苏联的发展方向，缺少对涡轮特性的预估方法。王永泓[15]针对快速预估涡轮特性的问题，以“从上而下”计算方法为基础，提出一种“从下而上”的计算方法，为涡轮特性预估提供了一种误差逐级递减的涡轮特性预估模型。屈彬[16]通过计算某型燃气轮机的特性，在此基础上创建了燃气轮机仿真模型，并编写了预估特性的计算软件。Lu 等[17]提出了一种基于Levenberg-Marquardt算法的涡扇发动机故障诊断方法，实现了涡扇发动机特性预估和故障诊断的精确评估。卫明[18]总结归纳了亚临界和超临界状态下的损失模型，并改进了亚临界和超临界状态下有、无空气冷却的损失模型，进而提高了跨声速轴流涡轮特性预估的准确性。

目前，针对跨声速涡轮的特性预估缺少相应的研究和算例。对涡轮特性进行预估主要有一维、准三维和三维方法，一维软件的计算量小，三维仿真精度高[19]。为此，本文拟采用一维软件对跨声速轴流涡轮特性进行预估，判断临界位置，计算跨声速涡轮的相关参数，并通过软件验证结果的准确性。

1 跨声速涡轮特性

跨声速涡轮的设计叶型可以是收缩型也可以是缩放型。但对于跨声速轴流涡轮或超声速轴流涡轮，缩放型叶栅的工况性能较差。本文采用一级渐缩型叶栅，利用斜切部分的膨胀作用满足超声速的要求。编程采用的Kacker & Okapuu 损失模型具体公式可参见文献[20-21]。

1.1 速度系数及落后角的修正

涡轮在非设计状态下工作时，由于工作状态的改变，动、静叶进口处的攻角发生变化，因而需要修正速度系数[22]：

式中：Mc1为静叶出口马赫数；φ为静叶的速度损失系数；φd为修正之前的静叶速度损失系数。

跨声速下马赫数对速度损失系数的修正：

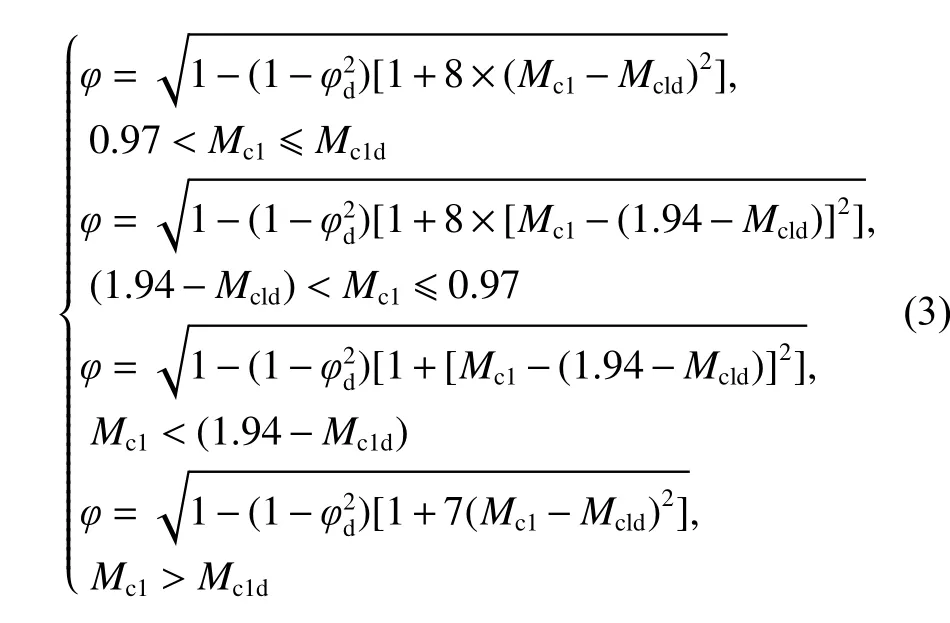
式中，Mc1d为设计工况下静叶出口马赫数。

非设计状态下出口气流角的修正[24]：

1.2 跨声速轴流涡轮流通公式及临界界面判断

跨声速涡轮的特性计算需要满足3 条基本假设：1）气流稳定同时沿轴向的对称性良好；2）参考直径上的流动能代表本级的流动；3）在涡轮的特性预估中绝热指数k和比热容Cp可近似视为常数。文中对于亚声速和跨声速涡轮流通方程的具体推导过程参见文献[18]。

亚临界涡轮基本流通方程可归纳为如下方程组：

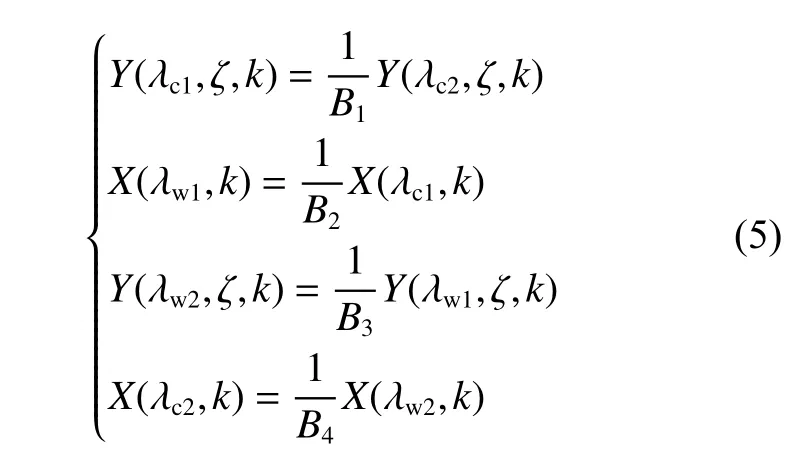
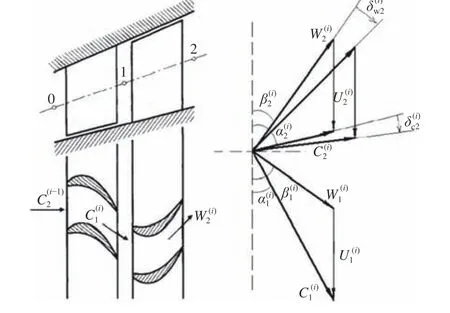
图1 超临界条件下轴流涡轮速度三角形示意图Fig. 1 Schematic diagram of velocity triangles for axial flow turbine under supercritical conditions

1.3 计算流程图

本文采用单级涡轮，采用“从上而下”的方式计算跨声速涡轮特性。流程如图2 所示，具体步骤如下：

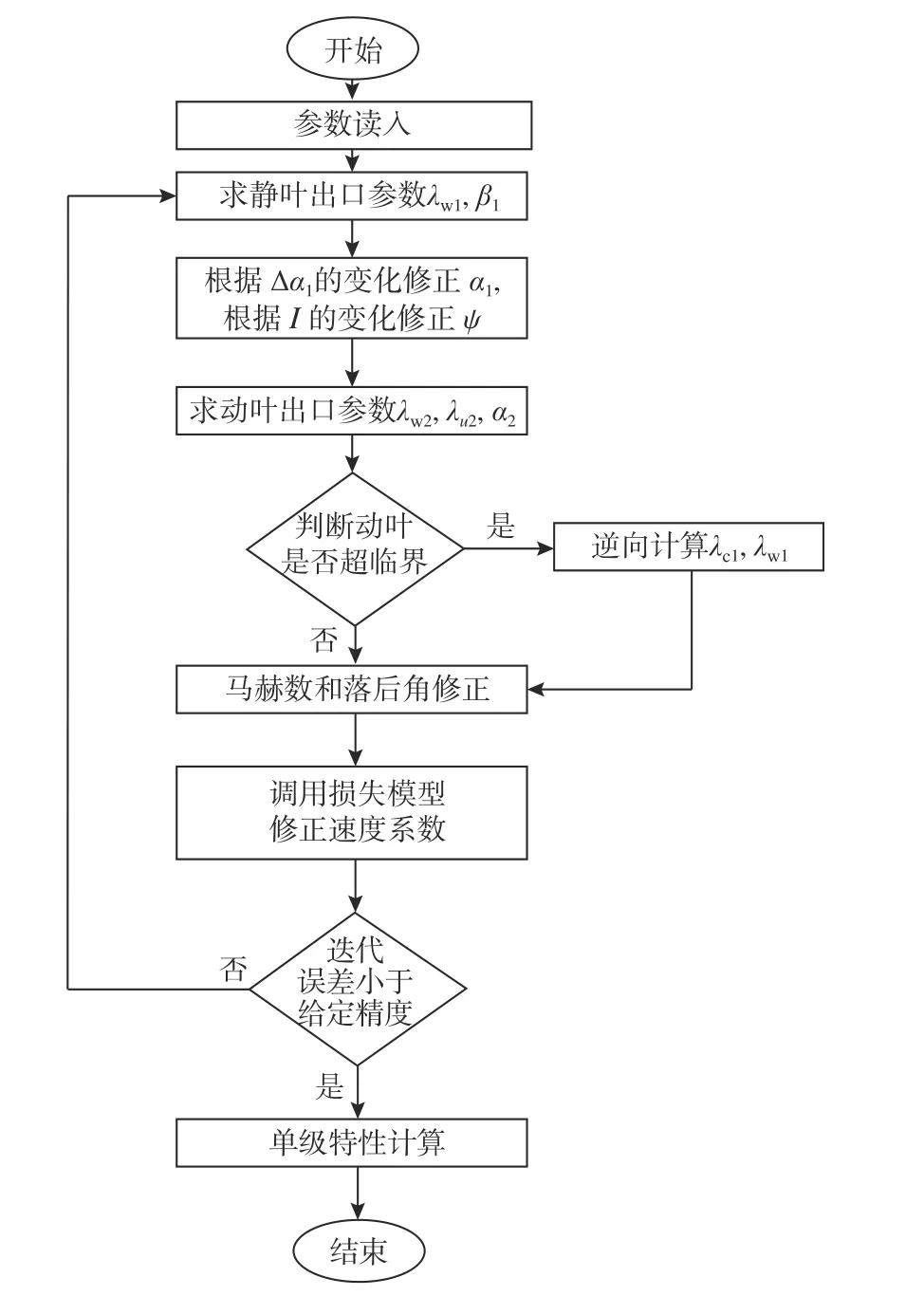
图2 跨声速涡轮特性计算流程图Fig. 2 Characteristics calculation flowchart of transonic turbine

1） 给定 λc1，通过初始参数计算出进口圆周速度 λu1。

2） 通过 α1和 λu1求 解动叶进口角 β1。

3） 通过新的气动函数X(λ,k)求 解 λw1。

4） 通过新的气动函数Y(λ,ζ,k)求 解 λw2。

5） 通过 λu1， λw1和 λc1求 解出口圆周速度 λu2。

6） 通过 λu2， λw2和 β2求 解 α2。

7） 通过新的气动函数X(λ,k)求 解 λc2。

涡轮级特性与 λc1， λw1， λw2和 λc2有关，只要求出这4 个参数便可计算涡轮特性参数。

2 跨声速轴流涡轮特性计算结果

2.1 结果对比及速度三角形绘制

基于K-O 损失模型以及涡轮特性计算方程，采用C#语言在VS 平台上进行编译。在.Net 框架下用Winform中的Label控件、TextBox控件、Button控件和DataGridView 控件进行界面的搭建，通过DataGridView 控件和Panel 来表示特性计算的结果及绘制速度三角形，界面如图3 所示。一维特性预估及三维仿真计算结果如表1所示。

图3 控制界面和参数输入Fig. 3 Control interface and parameter input

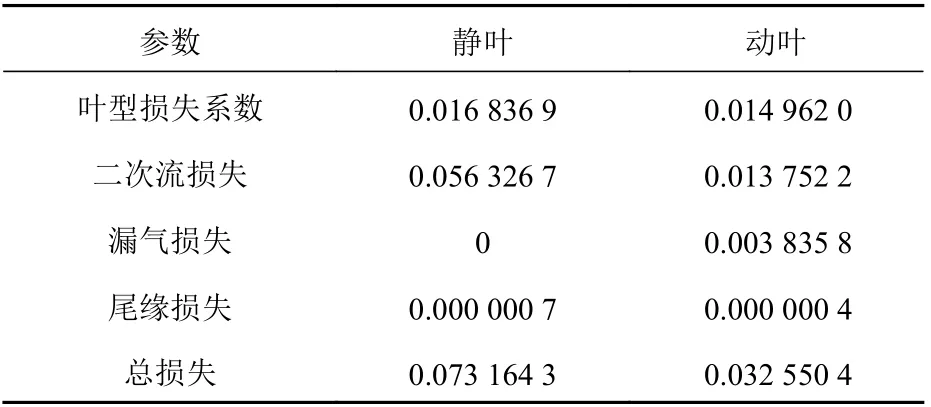
表1 损失模型计算结果Table 1 Calculation results of loss model

本文采用涡轮叶片的设计工况，对一维特性预估结果和三维仿真结果进行对比。通过表2 所示数据可以发现，三维的级等熵滞止温比与一维的相对误差为11.53%，级滞止膨胀比的相对误差为11.77%，反动度的相对误差为14.23%。此三者的误差较小，其他参数的相对误差略高，但一维的特性预估计算量相比于三维仿真结果少了几个数量级，对于跨声速涡轮的特性预估具有参考价值。

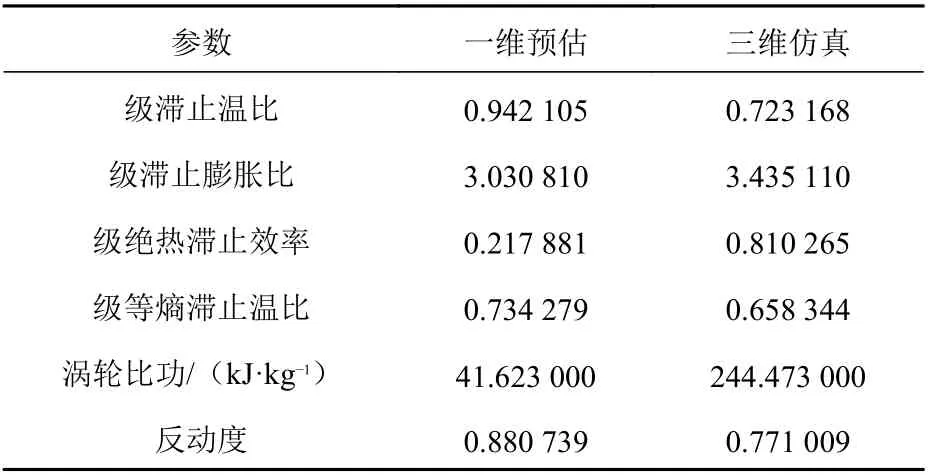
表2 涡轮特性参数计算结果Table 2 Turbine characteristic parameter calculation results

一维特性预估速度三角形如图4 所示。

在设计工况下，涡轮静叶的设计马赫数为1.21，涡轮动叶的设计马赫数为0.96。计算得到进、出口的无因次速度 λc1=1.12和 λw2=0.95，根据式（9）和式（10），判断出在动、静叶中均存在跨声速涡轮的临界界面。由图4 可见，只要动叶中存在临界界面，则动叶进口绝对速度（即静叶的绝对出口速度）会达到声速。对比图5的三维计算云图可知，在动、静叶的斜切部分由于存在膨胀波，即使背压低于临界压力，却仍然具有将气体加速到声速的能力。

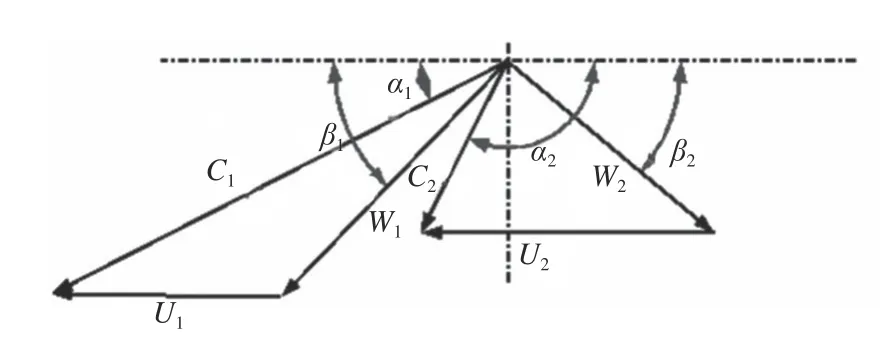
图4 速度三角形Fig. 4 Schematic diagram of velocity triangles

图5 CFX 马赫数数值模拟结果Fig. 5 Simulation result of CFX Mach number

在新的气动函数中，绝热指数是函数计算的桥梁，其值的选取是否合理直接影响了无因次速度的计算精度。图6 所示为在静、动叶的前、中、后6 个不同位置的绝热指数变化情况。通过对比可见，绝热指数在静、动叶尾缘的变化相对剧烈。在一维特性预估结果中，以静叶进口的绝热指数计算反动度的相对误差为14.23%，以动叶出口的绝热指数计算反动度的误差为13.70%，相对误差减小了0.53%。数值仿真中，高压涡轮绝热指数取值为1.33，低压涡轮取值为1.4，动力涡轮取值为1.5。

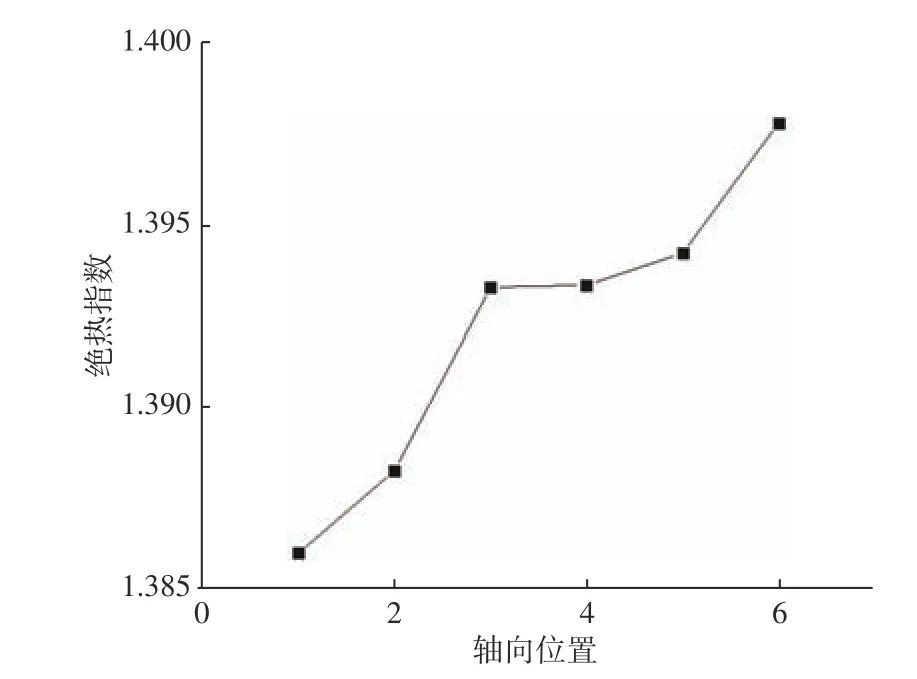
图6 绝热指数沿轴向的变化Fig. 6 Variation of the adiabatic index along the axial direction

2.2 误差分析

本文采用一维计算方法对跨声速涡轮设计点条件下的特性进行预估，采用三维软件进行验证。其中，级等熵滞止温比、级滞止膨胀比和反动度的相对误差较小，其他误差略大，分析其原因如下：

1） 算例采用一维编程和三维商业软件进行验证，其本身都是计算结果，与真实值相比都存在误差。

2） 计算机和变量类型的限制使得程序无法计算出比变量类型精度更小的数。

3） 算例是一级跨声速轴流涡轮，采用的是“从上而下”的计算方法，比“从下而上”方法的误差大。

4） 算例中绝热指数选取以静叶进口为基准，但对于动叶出口的绝热指数所计算的特性预估值，误差略有增大。

3 结 论

无论是航空还是船舶的燃气轮机，单级涡轮向高温、高效发展是大势所需，对跨声速乃至超声速的涡轮特性进行快速预估必不可少。本文采用一维编程对跨声速涡轮在设计工况下的特性进行了预估计算，在保证误差处于允许范围内的同时，减少了三维计算所需的网格划分验证和三维计算时间。此外，还对跨声速涡轮工作状态进行了预估计。得到了如下结论：

1） 采用所提涡轮特性预估的详细步骤，分析得到了特性预估程序与三维计算结果的误差产生原因。对于跨声速叶片，在设计工况条件下可采用出口马赫数和进口攻角修正速度损失系数及落后角。

2） 一维涡轮特性预估结果与三维计算结果的对比表明，二者存在误差。其中，一维特性评估得到的级等熵滞止温比与三维的相对误差为11.53%，级滞止膨胀比的相对误差为11.77%，反动度的相对误差为14.23%。在误差允许范围内，可以实现跨声速涡轮特性的快速预估。

3） 涡轮特性预估中绝热指数为常数，以涡轮出口温度得到的绝热指数相对于涡轮进口温度，反动度误差减低0.53%。合理选取绝热指数可以提高特性预估的准确性。