近冰面航行潜艇阻力及绕流场分析

柏铁朝，许建，王国栋，余琨，胡笑寒

1 中国舰船研究设计中心，湖北 武汉 430064

2 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

0 引 言

作为海军的重要作战力量，潜艇的隐蔽性使其具有强大的威慑力，其探测与反探测研究一直受到海军强国的高度重视[1]。极地环境的复杂性使得潜艇在冰区的航行情况与自由水域相比差异较大。冰面的覆盖改变了水面处的边界条件，并且考虑到潜艇航行时产生的挠曲重力波，有可能导致冰面破碎，从而使航行情况更为复杂[2]。因此，研究挠曲重力波对冰面的影响，对执行军事任务具有重要意义，对潜艇近冰面航行的水动力特性分析也十分重要。

在潜艇水动力分析研究初期，主要是致力于无界黏性流域条件下的情况。截至20 世纪80 年代中期，许多国家进行了大量的数值研究，其在原有势流计算方法和切片理论的基础上予以发展，考虑了自由液面带来的影响[3]。至20 世纪80年代后期，美国国防先期研究计划局（DARPA）发起建立了带各种典型附体的轴对称回转体流场试验数据库[4]。近年来，针对潜艇近自由液面航行的研究开始逐渐增多，并以数值研究为主。Jagadeesh 等[5]基于RANS 方法，讨论了自由液面对回转体潜艇模型航行的影响。Saout 等[6]针对潜艇近自由液面航行时的稳定性进行了研究。Dawson[7]就浸没深度、速度和细长比对流线型对称体潜艇与自由液面的相互作用开展了相关试验和数值研究。

我国对潜艇水动力性能的研究主要集中在对Suboff 潜艇全附体模型阻力、升力、表面压力及精细流场的数值计算上。李艳等[8]基于RANS方法，将湍流模型与壁面函数法相结合，对Suboff全附体潜艇模型进行了数值模拟，并将计算值与试验值进行对比，验证了模拟方法的准确性。张楠等[9-10]基于RANS 方法，结合流体体积（volume of fluid，VOF）法，分别计算了Suboff 近自由液面航行时的阻力以及各潜深下的增阻系数、艇−桨干扰特性，并讨论了围壳对自由液面兴波的影响。邱云明和邓锐[11]对Suboff 全附体潜艇模型近水面航行时的兴波进行了多工况下的计算，并对比了各弗劳德数下的自由液面波形和中纵剖面上的波高。

然而，无论国内还是国外，少有关于Suboff 潜艇模型在冰面下航行时的流场特性及其规律研究。而对冰区潜艇近冰面航行进行数值模拟，掌握其阻力与流场特性进而探索挠曲重力波破冰方法意义重大。

为了系统分析潜艇近冰面航行时的阻力及流场分布规律，本文拟以Suboff 全附体潜艇模型为研究对象，在STAR-CCM+软件中应用RANS 方法计算艇体的水动力性能，然后对不同潜深、航速等条件下艇体近冰面航行时的阻力系数、表面压力系数、表面摩擦系数以及艇体绕流场特性进行分析。

1 数值方法

1.1 基本控制方程

对于计算流体力学问题，相关的控制方程包括质量守恒方程和动量方程。

质量守恒方程：

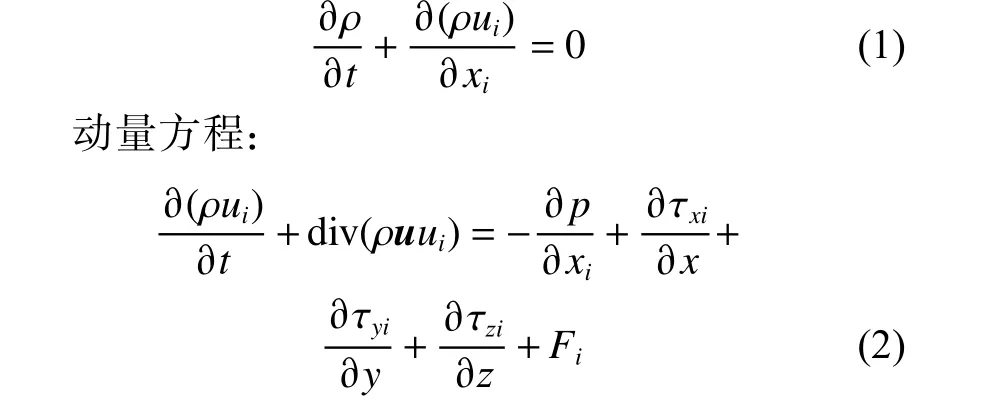
式中：ρ 为流体密度；ui为速度矢量在3 个方向的速度分量；xi为基于速度分量的3 个方向的位移；u为速度矢量；p为压强；Fi为质量力；t为时间；τxi，τyi，τzi为黏性应力τ 的分量。

1.2 湍流模型

本文所使用的湍流模型为SSTk-ω 模型[12-13]。其中湍流动能k的输运方程为：

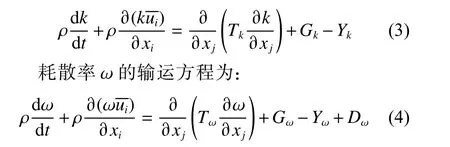
式中：xj为基于湍流动能和耗散率的3 个方向的位移；Gk为由层流速度梯度产生的湍流动能；Gω为由ω 方程产生的湍流动能；Tk和Tω分别为k和ω的扩散率；Yk和Yω为由扩散产生的湍流；Dω为正交发散项。

2 物理条件设置

2.1 计算对象参数

本文以美国DARPA 提出的Suboff 全附体潜艇模型为研究对象，其几何模型及参数分别如图1 和表1 所示。

2.2 计算域及边界条件设置

图1 Suboff 潜艇几何模型Fig. 1 Geometric model of Suboff submarine model

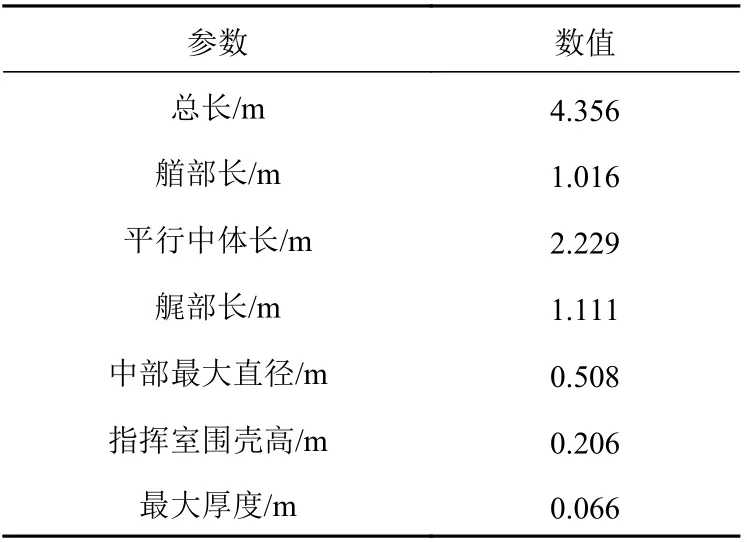
表1 Suboff 全附体潜艇模型几何参数[10]Table 1 Geometric parameters of Suboff submarine model

由于所采用的Suboff 全附体潜艇模型和流域为对称的，所以通过设置对称面计算一半的流域即可。

潜艇近冰面航行时，在潜艇穿过冰盖下某一位置的瞬间，可以认为冰盖尚未变形，或者是其变形对潜艇绕流场的影响微弱，因此，将艇体上方边界设置为无滑移壁面边界。为了模拟无限流域的物理背景，将来流出口设置为压力出口，潜艇中纵剖面设置为对称面，潜艇表面设置为无滑移壁面。为保证计算稳定性，其余边界设置为速度进口。具体边界条件的设置如图2 所示。图中，L为艇体长度，d为模型潜深大小。

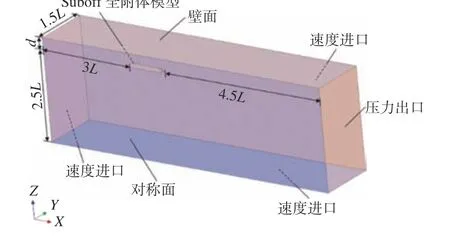
图2 Suboff 潜艇近冰面航行边界条件Fig. 2 The Suboff submarine model's boundary condition when sailing near the ice surface

2.3 网格收敛性分析

本文采用3 种不同的网格尺寸进行验证。在划分网格时，通过调整网格的基本尺寸，可以在不改变网格相对尺寸的条件下，改变网格的疏密程度。对艇体加密时，选择面网格加密方法，并将艇体表面分割为指挥室围壳、尾翼和艇体3 部分进行计算。采用的网格分为3 套，其基础尺寸分别为0.8，1.0 和1.2 m，各基础尺寸下的网格数量信息（半侧计算域）如表2 所示。边界层取10 层，Y+值为30，考察艇体前进方向所受的阻力。计算域的网格划分如图3 所示。

目前，直航全附体潜艇阻力测试普遍参照的是1998 年美国海军水面战中心卡德洛克分部（NSWC）[14]提出的不同航速下所对应的总阻力试验值。选择航行速度V=3.05 和5.14 m/s 进行网格无关性验证时，各网格尺度下的计算结果及误差如表3 和表4 所示。

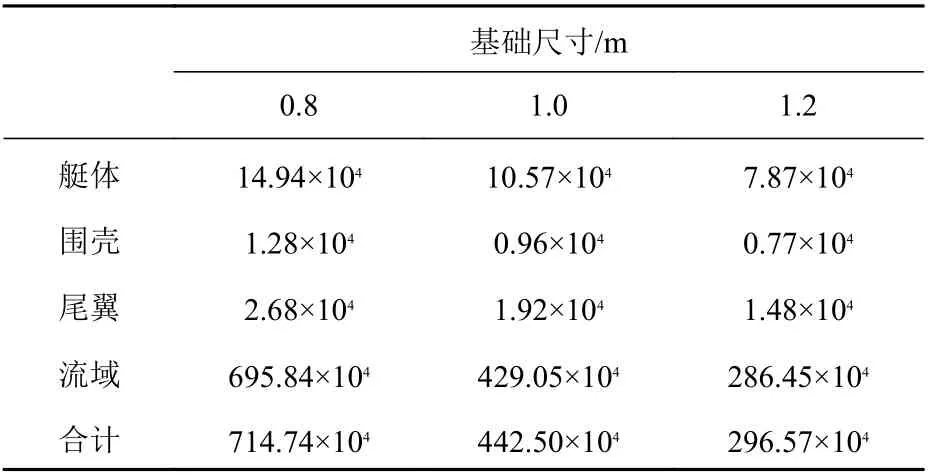
表2 不同基础尺寸下的网格数量Table 2 The number of grids with different base sizes

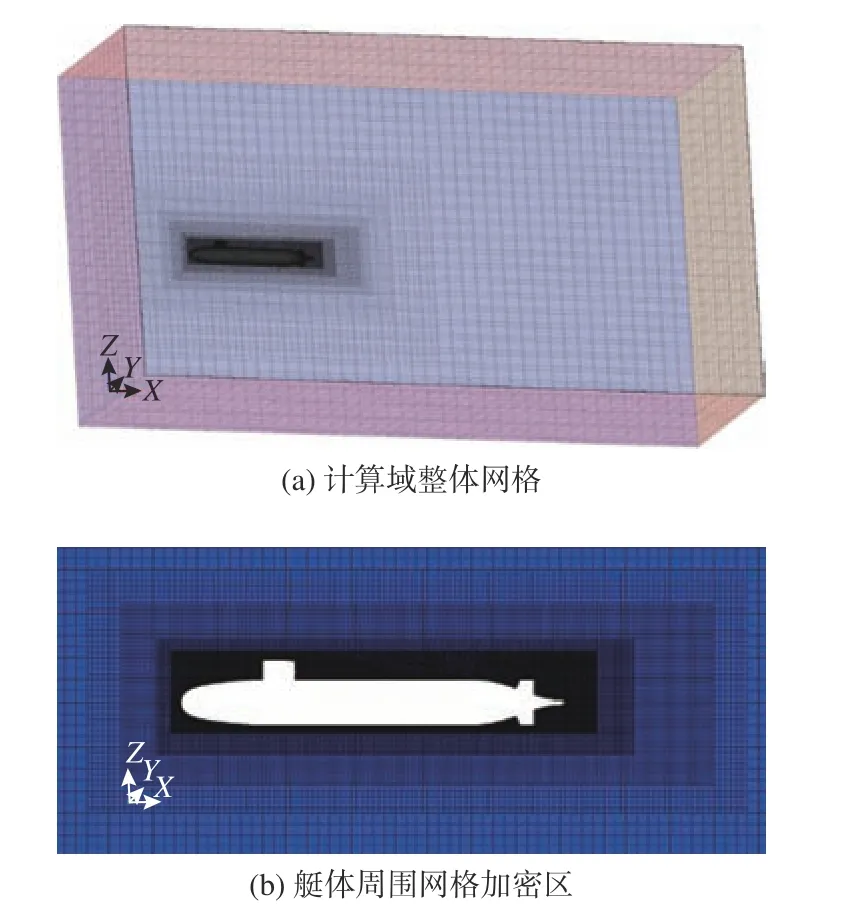
图3 计算域网格划分Fig. 3 Grid division of computational domain

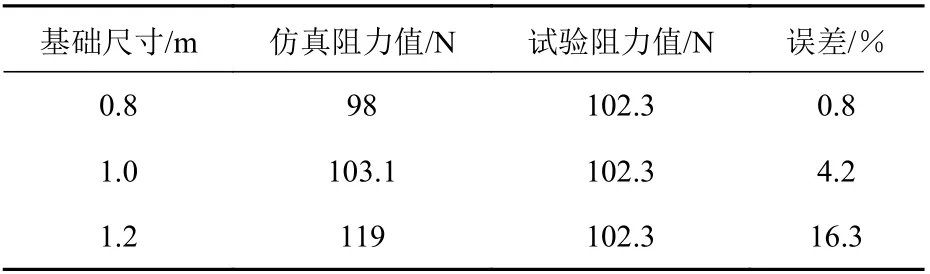
表3 V=3.05 m/s 时的阻力计算值及误差Table 3 Calculated resistance values and errors at V=3.05 m/s

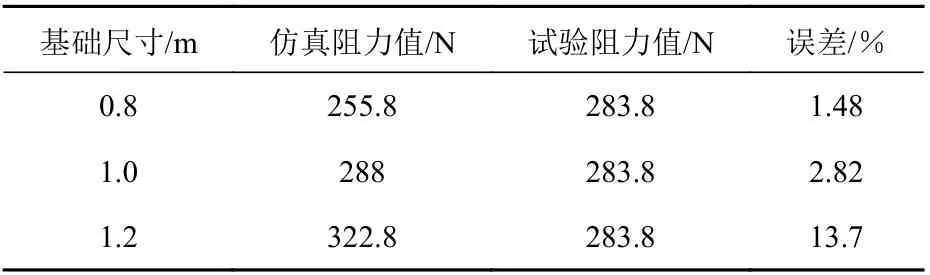
表4 V=5.14 m/s 时的阻力计算值及误差Table 4 Calculated resistance values and errors at V=5.14 m/s

无关性仿真计算结果与实体试验的比较说明网格尺寸为单调收敛，将选择误差最小的基础尺寸0.8 m 作为Suboff 潜艇模型变参数仿真计算的网格划分参数。

2.4 计算方法验证

为了验证本文数值模拟方法的可靠性，设置了多个航行速度，用以计算无界绕流条件下Suboff全附体潜艇模型的直航阻力值，并与文献[4]中的试验数据进行了对比，结果如图4 所示。

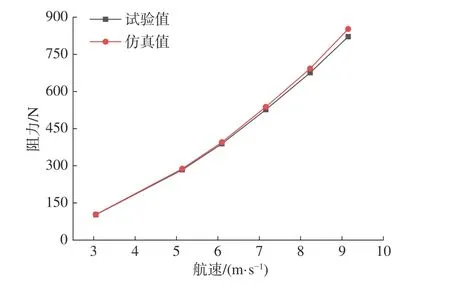
图4 试验与数值模拟阻力值对比Fig. 4 Comparison of experimental and numerical simulation resistance values

由图4 可以看出，仿真值和试验值均是随航速的增加而增加的，二者吻合较好，仿真值只在较高航速时略高于试验值，整体来说误差控制在2%以内，验证了本文采用方法的可行性。

2.5 近冰面航行计算模型建立方法验证

由于基于重叠网格的方法（方法1），也即采用潜艇在静止的冰面下直线航行的计算模型开展数值计算的方法，存在计算资源耗费大、计算速度过慢及计算结果不易收敛的问题，所以在实际计算中采用的是潜艇在均匀来流中的水动力性能分析方法（方法2）来模拟艇−冰−流之间的相互作用，由此避免重叠网格的应用，降低计算难度并提高计算速度。这种方法的几何模型及网格划分示意图如图5 所示。

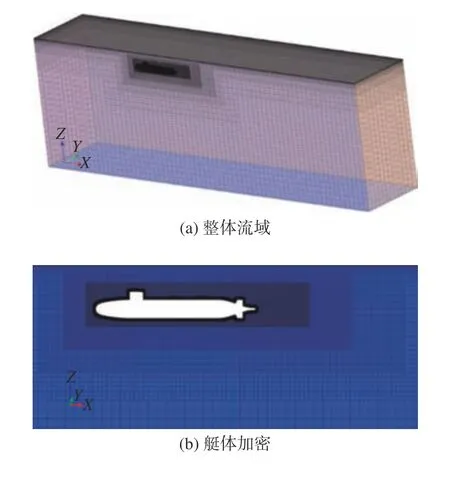
图5 近冰面航行计算域网格Fig. 5 Computational domain grid when sailing near ice surface

但是，采用艇不动的方法（方法2）会消除艇与冰面之间的相对运动。针对这一缺陷，分别提取基于方法1 和方法2 这2 种方法计算得到的潜艇航行阻力、艇体表面压力分布、中纵剖面上半缘线压力系数分布及冰面下表面压力分布结果进行了对比验证，以此确认方法2 中计算模型设置对计算结果的影响程度。各计算结果的对比如表5 和图6、图7 所示。计算工况选择较高航速V=5.29 m/s（潜艇以较高航速航行时对计算方法的准确性及稳定性要求较高，作为方法1/方法2 的对比验证计算工况较为合理）下的不同潜深（d=1.67，2.08 m）。观察表5，发现在不同潜深下，相比于方法1，方法2 在潜艇阻力计算结果上的偏差均在3%以内。

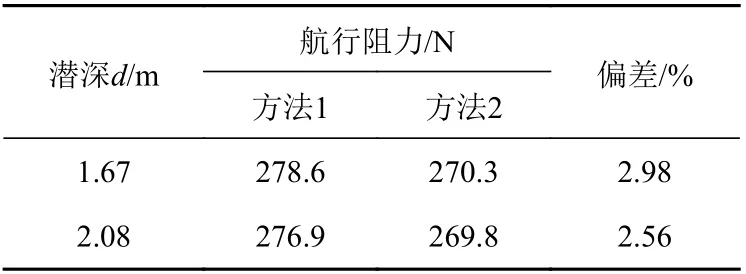
表5 V=5.29 m/s 时不同潜深下潜艇航行阻力计算结果对比Table 5 Comparison of computational results of submarine navigation resistance under different submergence depths when V=5.29 m/s

为了更加精确地对比2 种计算方法对艇体表面压力的影响，提取了各方法下艇体中纵剖面上半缘线的表面压力系数CP分布，如图6 所示（图中，横坐标为艇不同横向位置的无因次值）。由图可见，基于方法1 和方法2 得到的艇体中纵剖面表面压力系数分布基本相同，仅在围壳后端、尾翼、艇艉型线收缩处出现了略大的差异。与方法1 的计算结果相比，基于方法2 计算的艇体中纵剖面上半缘线表面压力系数偏差在1.6%以内。

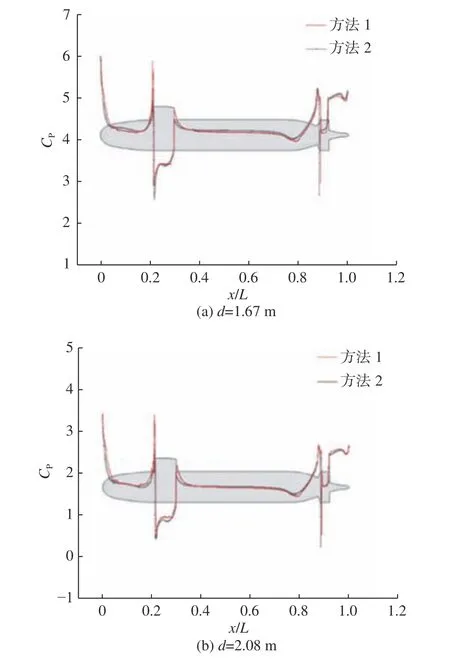
图6 V=5.29 m/s 时不同潜深下潜艇中纵剖面上半缘线表面压力系数Cp 分布对比Fig. 6 The Cp of the upper submarine mid profile under different submergence depths when V=5.29 m/s

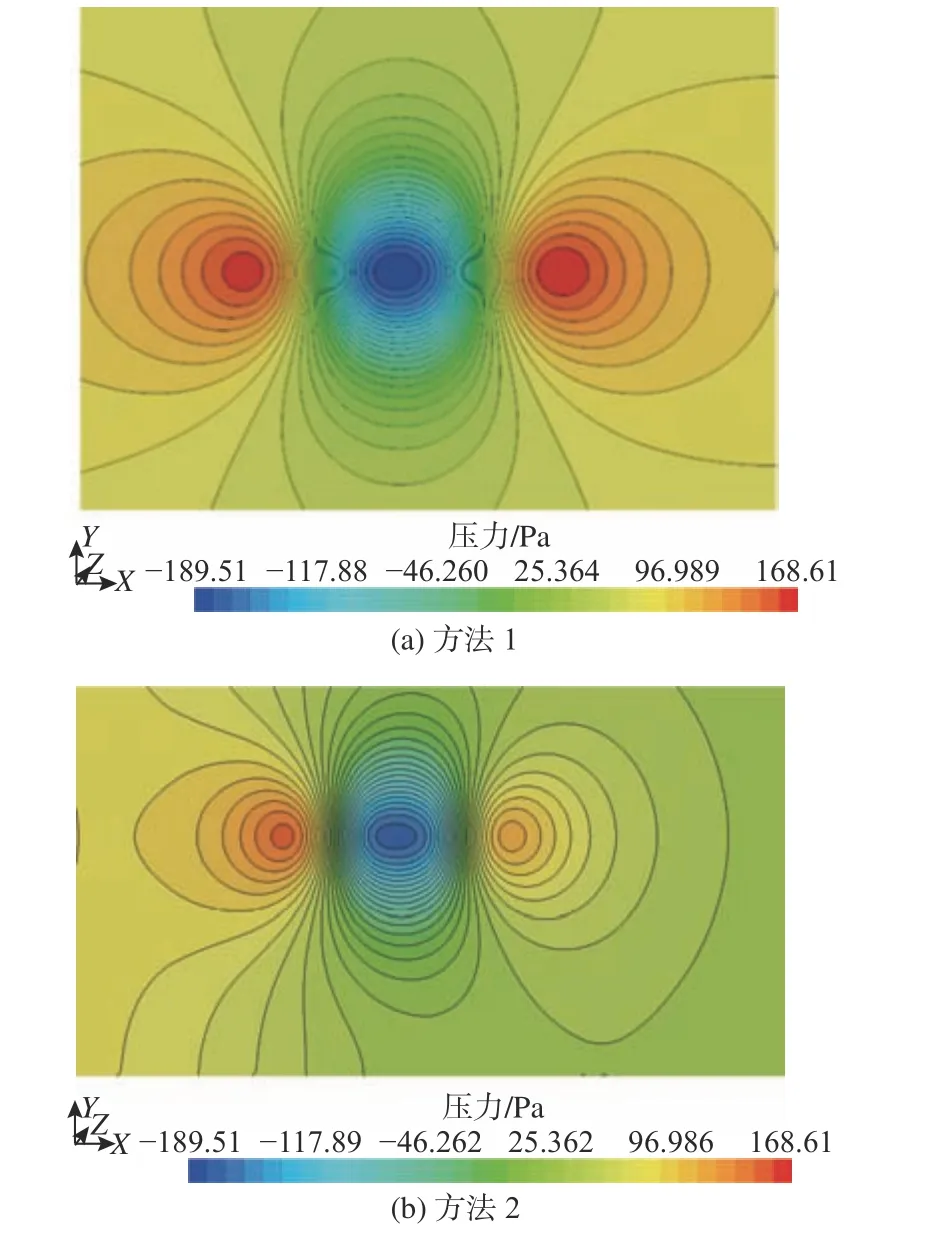
图7 V=5.29 m/s，d=1.67 m 时方法1/方法2 冰面下表面压力分布对比Fig. 7 Comparison of pressure distribution between method 1 and method 2 at V=5.29 m/s，d=1.67 m

图7 所示为航速V=5.29 m/s、潜深d=1.67 m时，基于2 种计算方法得到的冰面下表面压力分布云图。其中，横坐标为艇不同横向位置的无因次值，纵坐标为2 种计算方法所得到的压力系数的物理值。由图可见，采用2 种计算方法得到的冰面下表面压力分布形态基本一致，因艇体与冰面之间的水流流速较快，导致冰面在艇体上方出现了环状低压区，并在低压区的前、后方出现了环状高压区，这种压差在一定程度上会导致冰板的形变。对比图7(a) 与图7(b) 可见，采用方法2模拟潜艇近冰面航行冰面所受到的影响时，计算模型的设计缺陷并未对结果形成较大的干扰。

综上，考虑到采用方法1 开展潜艇近冰面航行计算资源耗费较大、计算速度过低，因此在有限的计算资源与时间条件下，本文将选择方法2作为潜艇近冰面航行数值模拟的计算方法。对于方法2 在计算模型设置上存在的缺陷，通过对潜艇航行阻力、艇体表面压力系数及冰面下表面压力分布计算结果的对比验证，证明此缺陷对近冰面航行潜艇的阻力、绕流场及冰面下表面压力的数值模拟结果影响较小，不影响方法2 的可行性。

2.6 计算工况设置

参考Pogorelova 等[15]对潜艇在弹性板下运动的试验研究，数值模拟的工况在实尺度上与该试验中的工况设置一致，如表6 所示。表中，Fr为艇长弗劳德数，d为Suboff 潜艇航行深度（艇体中轴线至冰面下表面的距离），D为艇体最大直径（本文计算模型取D=0.508 m）。

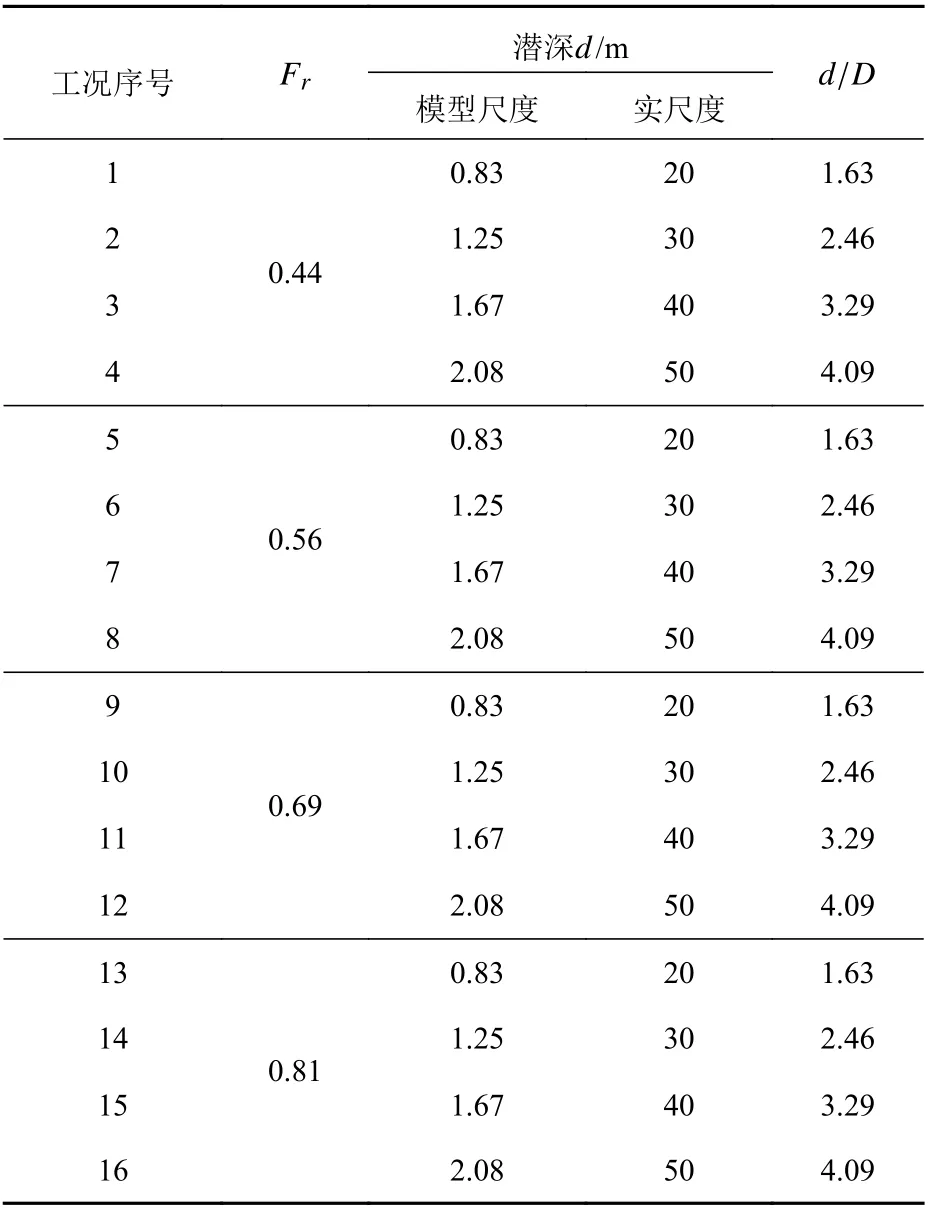
表6 各工况计算参数设置Table 6 Calculation parameter setting for each working condition

3 计算结果与分析

3.1 阻力预报结果分析

各工况下近冰面航行潜艇总阻力（单位：N）计算结果如表7 所示，各潜深下艇体的各成分阻力系数随弗劳德数Fr的变化规律如图8 所示。

其中，摩擦阻力系数CF，压阻力系数CVP和总阻力系数CT的定义如下：

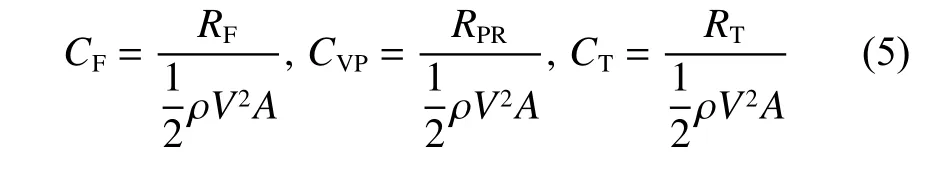
式中：RF，RPR，RT分别为艇体的摩擦阻力、压阻力和总阻力；ρ=998.16 kg/m3，为水密度；A为艇体湿表面积，由于本数值模拟时潜艇是完全浸入水中的，所以A为Suboff 全附体潜艇模型的表面积，A=6.361 m3。

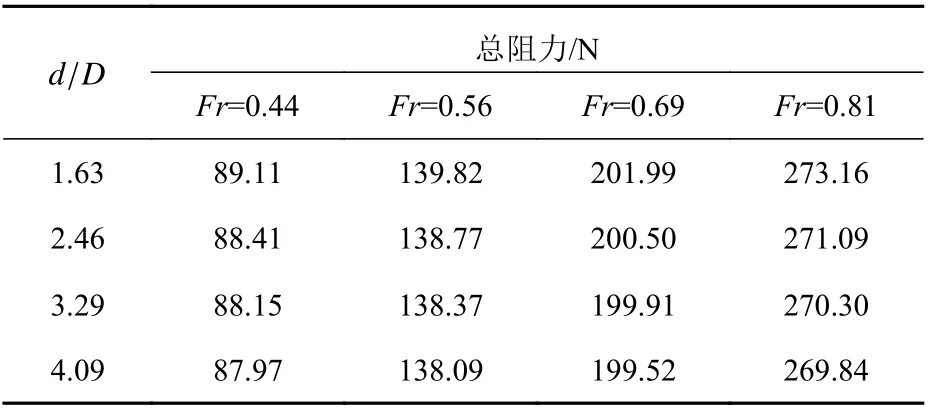
表7 各工况下近冰面航行Suboff 潜艇总阻力Table 7 The total resistance of Suboff model under different working conditions when sailing near the ice surface

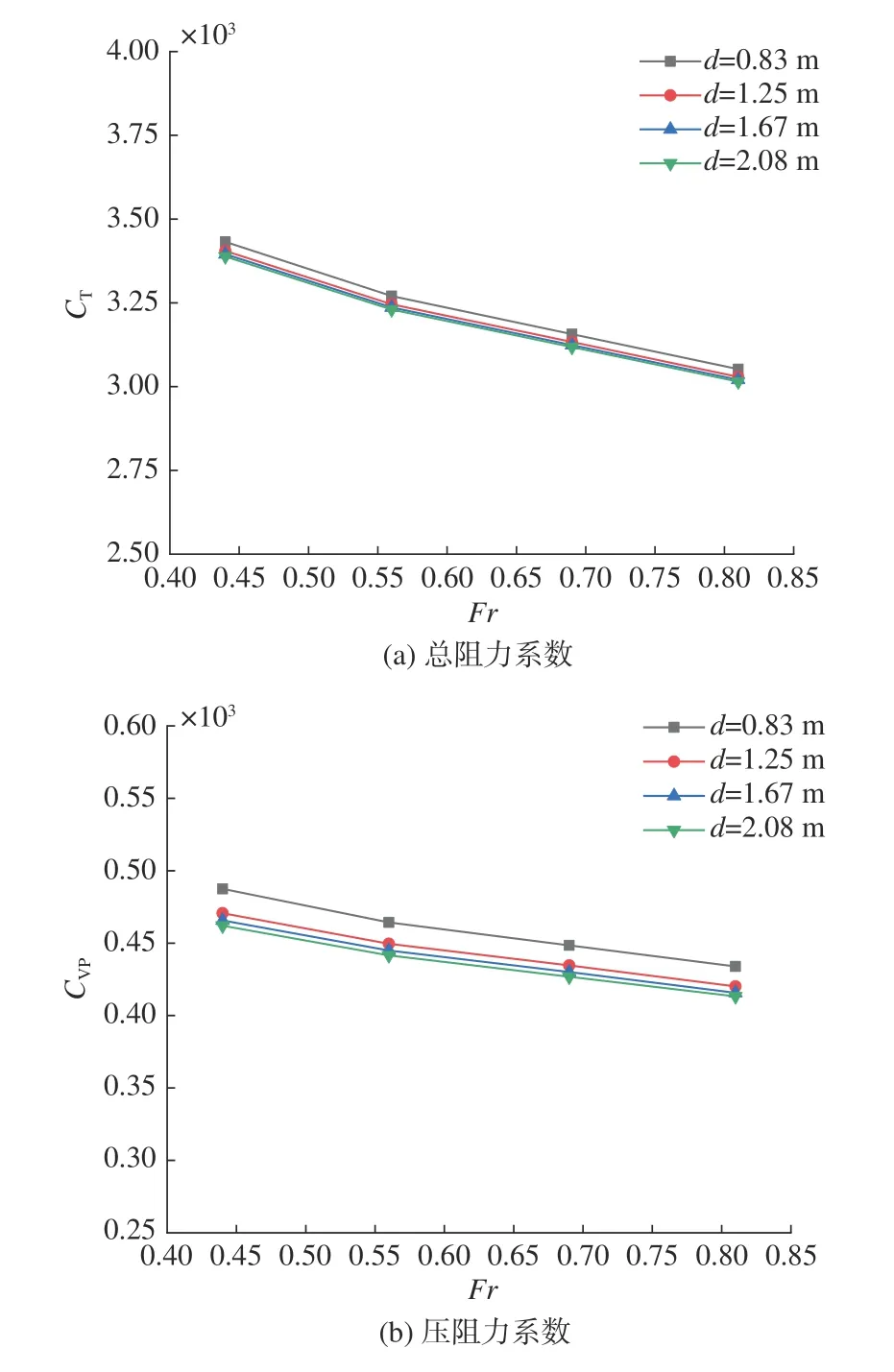
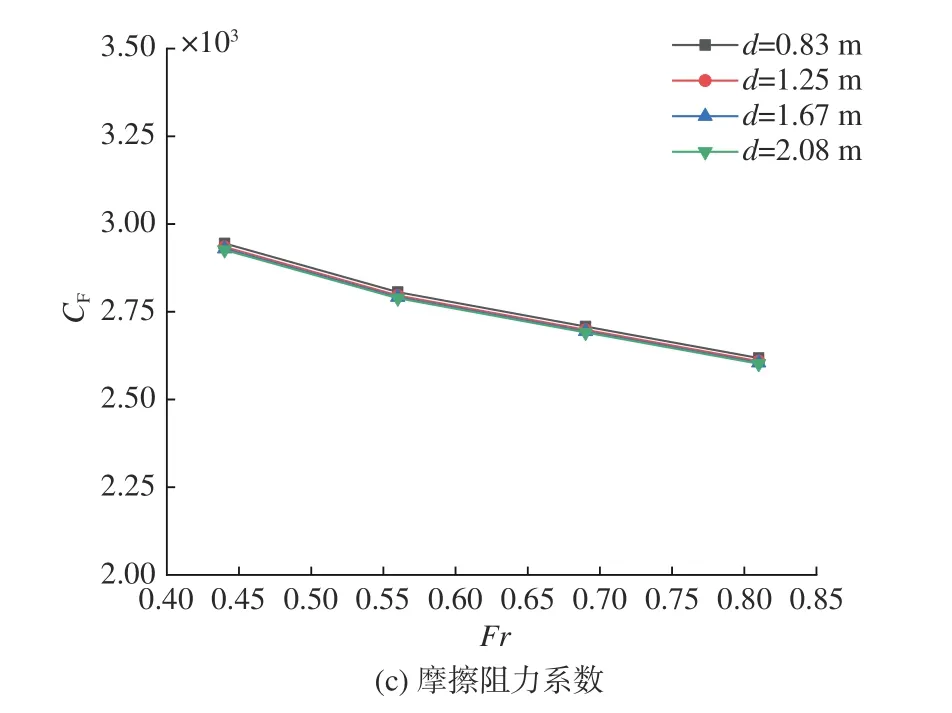
图8 不同工况下近冰面航行潜艇各成分阻力系数Fig. 8 The different composition of drag coefficient of Suboff under different working conditions when sailing near the ice surface

由图8(a)可知，潜艇的总阻力系数CT在同一弗劳德数Fr下随潜深d的增加而降低，在同一潜深d下随弗劳德数Fr的增加而降低。并且，在不同潜深下，艇体阻力系数随航速的变化趋势几乎相同。潜艇近冰面航行时，总阻力包括摩擦阻力和压阻力。对比图8(b)和图8(c)中的数值发现，潜艇近冰面航行时，在设计工况范围内，摩擦阻力系数CF占总阻力系数CT的主要部分。通过对潜艇周围阻力性质的分析不难得出，由于冰面的存在，使得艇体周围不存在兴波影响，因而减小了艇体所受到的压阻力；此外，由于艇体全部浸没于水中，且潜艇的湿表面积较大，故进一步削减了压阻力对总阻力的贡献。摩擦阻力为边界层内剪切应力的合力。由于壁面剪切应力τ 在湍流流态时正比于航速V3/2，所以壁面剪切应力τ 随V的增大情况小于V2关系，从而导致了局部摩擦阻力系数Cτ随航速的升高而降低的情况[16]。因为Cτ与CF的变化规律是一致的，所以，CF随航速的升高有降低趋势，这与图8(c)中CF随Fr的变化趋势是一致的。在各个潜深下，4 条曲线几乎重合，这说明在潜艇近冰面航行情况下，潜深对CF的影响很小，这一结论在文献[15]中得到了印证。

观察图8(b)并与摩擦阻力系数CF相比，发现压阻力系数CVP随潜深的变化较大。随着艇体逐渐远离冰面，CVP将逐渐降低，但随着潜深的增大，压阻力系数CVP的变化趋势逐渐减小。具体体现为，当潜深d=1.25，1.67 和2.08 m（d/D=2.46，3.29，4.09）时，所得到的艇体CVP值几乎没有变化，不过在最小潜深d=0.83 m（d/D=1.63）时CVP的变化相对较大。所以，在近冰面航行时，当d/D>1.63时，潜深几乎不影响艇体的阻力系数。

图9 提取了d=1.25 m 时近冰/水面航行时各成分阻力系数随Fr变化的曲线，以及Fr=0.56 时近冰/水面航行时各成分阻力系数随d变化的曲线。由图可见，与近水面边界条件相比，近冰面航行时的总阻力系数CT普遍偏小；各工况下近水/冰面航行艇体的摩擦阻力系数CF基本一致，近水/冰面航行时潜艇总阻力系数CT的差异主要体现在压阻力系数CVP随Fr及潜深d的变化形式上。观察图9 还可以发现，近冰面航行时，由于没有表面兴波对兴波阻力的影响，压阻力普遍小于近水面航行时的情况；在近水/冰面航行摩擦阻力系数基本相同的条件下，导致近冰面航行时艇体总阻力系数CT普遍偏小；此外，近冰面航行时Fr对CT影响的线性程度较大。

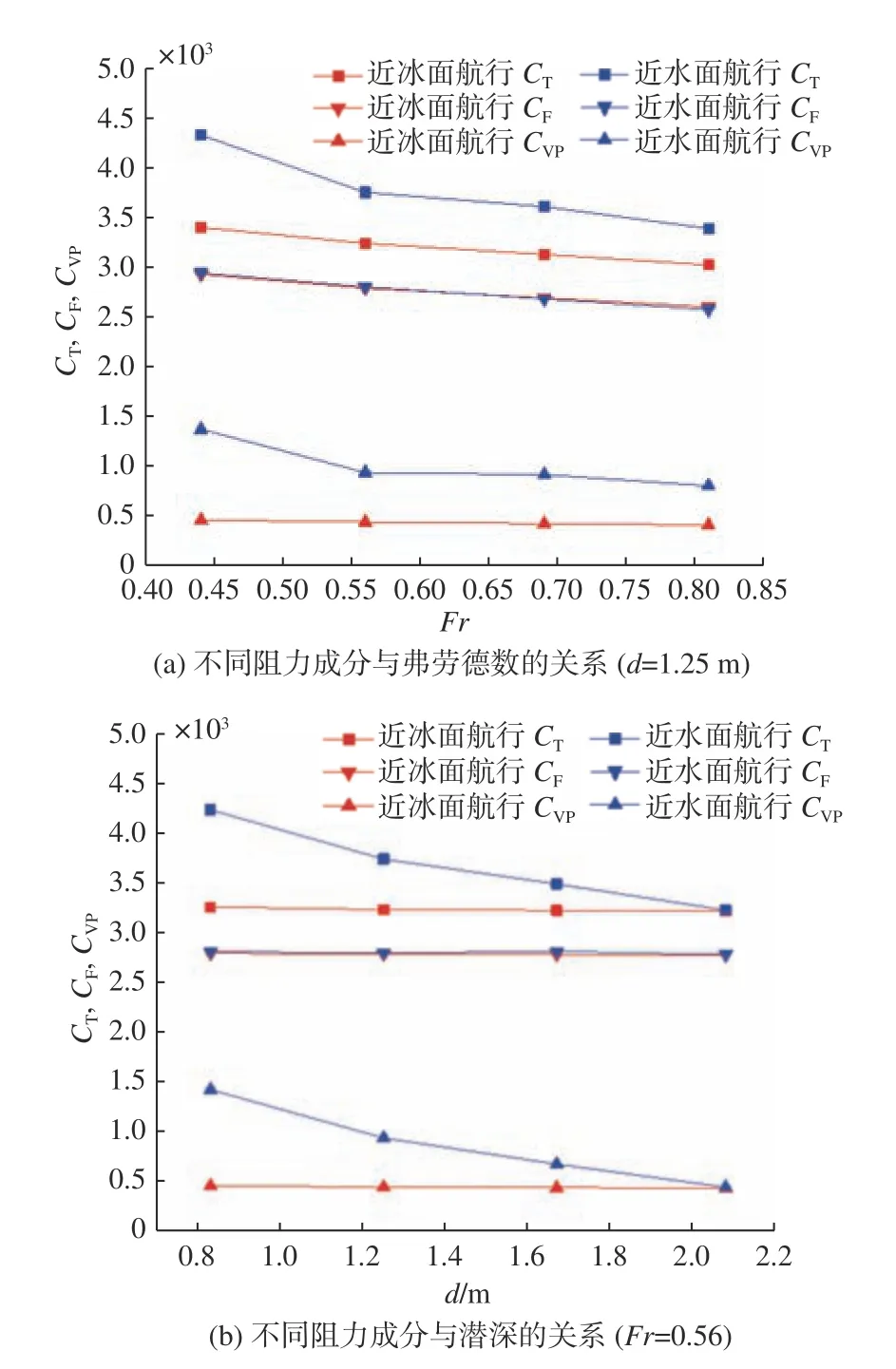
图9 各工况下潜艇近冰/水面航行时不同成分阻力系数的对比Fig. 9 The different composition of drag coefficient of Suboff under different working conditions when sailing near the ice/water surface

3.2 壁面压力/摩擦系数分析

3.2.1 监测位置及数值处理方法

表面压力系数CP和表面摩擦阻力系数Cf的定义如下：

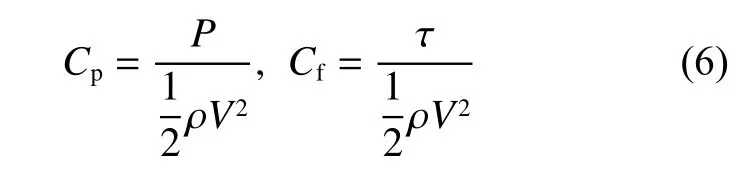
式中，P为表面压力。

本小节所选取的Suboff 潜艇艇体中纵剖面上缘线以及指挥室围壳和尾翼的不同截线位置如图10 所示。图中，H1为指挥室围壳截线与艇体之间的距离，H2为截线前端距离尾翼与艇体交线前缘点的距离；S为尾翼截面总高度。

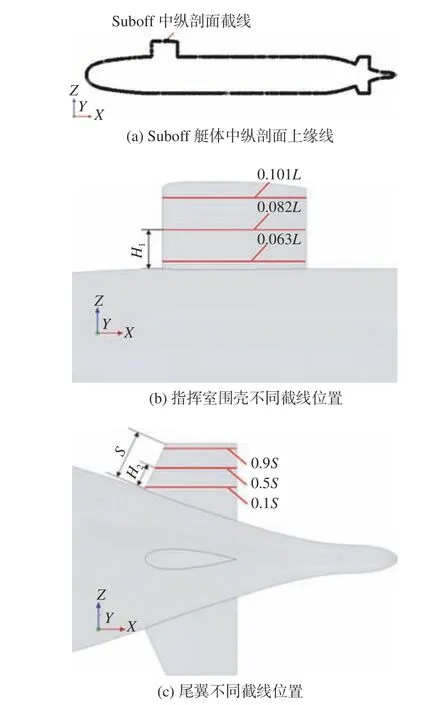
图10 潜艇相对应的截线位置Fig. 10 The transversal position of a submarine

3.2.2 中纵剖面上半缘线压力系数及摩擦力系数对比

图11 所示为近冰面航行状态下，Fr=0.56 时各潜深下的艇体中纵剖面上缘线表面压力系数分布曲线。图12 所示为d=1.25 m 时各弗劳德数下的艇体中纵剖面上缘线表面压力系数分布曲线。

由图11(a)可知，在各潜深下，Cp沿艇体分布的规律几乎相同，其随着潜深的均匀增加也呈均匀增加趋势。形成这一现象的原因主要是流体静压随潜深的线性变化，同时，由于冰面的存在，不存在兴波现象对艇体表面压力分布规律的影响。由图12(a)可知，潜艇以不同的航速航行时，Cp沿艇体分布的形式基本相同；随着弗劳德数的增加，Cp会有所下降，这与式(5)一致。而无论潜深和弗劳德数如何改变，艇体周围的摩擦阻力系数并不会产生较大的波动。因此，在考虑潜艇近冰面航行的表面压力系数时，应充分考虑航行速度和流体静压的影响。

此外，从图11 和图12 中还可以看出，在艇体型线变化剧烈的位置，其附近的表面压力系数Cp及摩擦阻力系数Cf变化较大，这主要体现在模型艏部，以及指挥室围壳前、后缘和尾翼的前缘。但从整体上来看，Cp和Cf在围壳处变化最大。

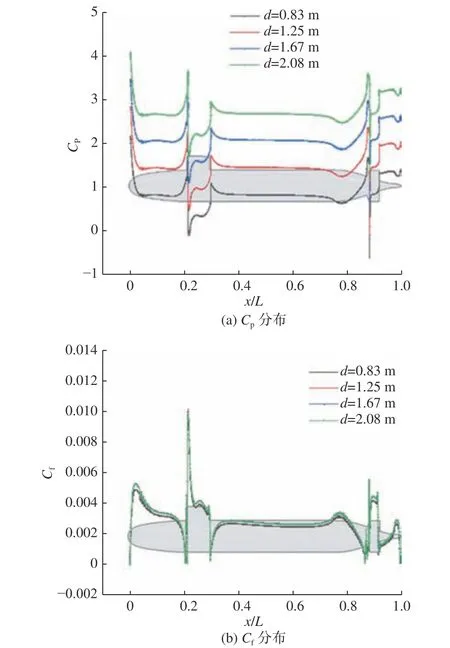
图11 近冰面航行时各潜深下艇体中纵剖面上缘线Cp 和Cf 的分布（Fr =0.56）Fig. 11 The Cp and Cf distribution of upper submarine mid profile under different submergence depths when sailing near the ice surface (Fr=0.56)

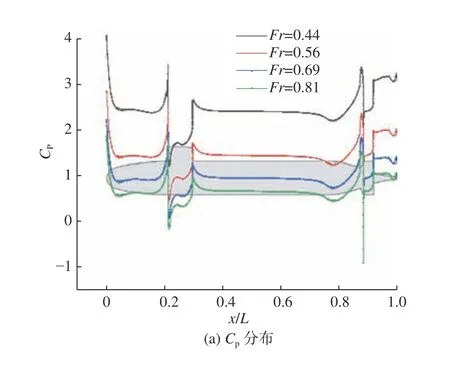
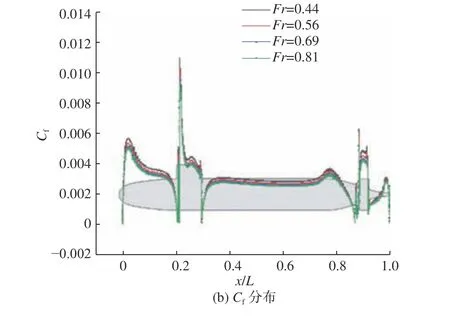
图12 近冰面航行时各弗劳德数下艇体中纵剖面上缘线Cp 和Cf 的分布（d=1.25 m）Fig. 12 The Cp and Cf distribution of upper submarine mid profile for different Froude numbers when sailing near the ice surface (d=1.25 m)

具体而言，Suboff 潜艇模型艏部、指挥室围壳前、后部以及尾翼附近的摩擦阻力较高，说明这几个区域的流速变化较大，因此在潜艇执行作业任务时需特别予以考虑。综合来看，在设计工况内，潜深及弗劳德数对Cf的影响较小，其随着弗劳德数的降低略有升高。

3.2.3 围壳及尾翼表面压力和摩擦阻力系数分析

近冰面航行时，指挥室围壳不同高度截线处表面压力系数分布沿截面弦长分布变化的规律如图13 和图14 所示。

考虑到截面具有对称性且在均匀来流中作直航运动，因此图13 和图14 只给出了截面一侧的压力分布，尾翼的情况亦是如此。为了形象说明各高度截线上各监测点在围壳、尾翼表面的位置，取了围壳、尾翼的横截面作为Cp分布曲线的背景。从图中可以看出，不同指挥室围壳在不同高度处截面的压力分布形式类似，Cp在前部和艉部出现了极大值，而在围壳中间区域由于型线形状变化出现了轻微波动，在型线过渡处出现了极小值。总体上，尾翼处型线的变化会使围壳中部附近的流体流速相对较快，压力相对较小。

由图13 可见，Cp的分布规律基本一致，在各弗劳德数Fr下是随潜深的增加而均匀增加的；Cp在同一工况下随截线高度的上升有微小的下降。由图14 可见，在围壳表面，航速对Cp的影响普遍呈一定程度的负相关；此外，在较高位置的围壳截线处，因Fr导致的Cp值差异变小。这说明相对于围壳顶部，航速对围壳底部与艇体连接处的影响更大，故在考虑潜艇安全性设计时应着重予以考虑。

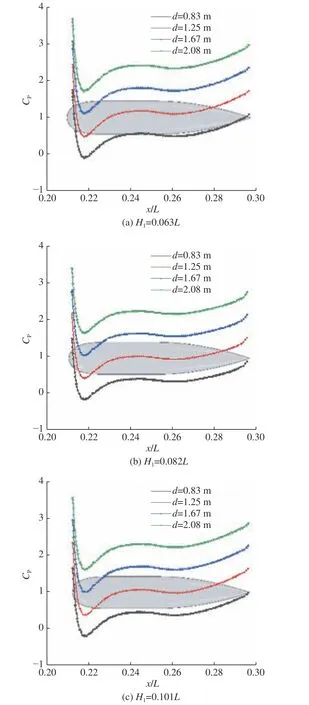
图13 近冰面航行时各潜深下指挥室围壳不同高度截线的Cp 分布对比（Fr =0.56）Fig. 13 The CP distribution of sail transversals at different heights for different submergence depths when sailing near the ice surface (Fr=0.56)

尾翼在不同高度截线处的表面压力系数变化如图15 和图16 所示（图中，L0为尾翼弦长的总长度，x0为尾翼不同位置x方向位置的分布）。与指挥室围壳压力分布形式不同，由于潜艇艉部流场较为紊乱，所以表面压力系数在尾翼各高度截线上的分布曲线其平滑程度较低。整体而言，尾翼前部与后部压力较大而中部压力较小，这一点与指挥室围壳的情形相似，因二者的横截面均为机翼型对称剖面。与艇艏部流场相比，艇艉部流场并非同艏部一样为增速减压区，这为边界层的分离提供了条件，使得尾翼剖面上的压力分布变化更为剧烈。该剧烈程度不是从最大值与最小值之差看出，而是从压力分布的脉动剧烈程度看出。

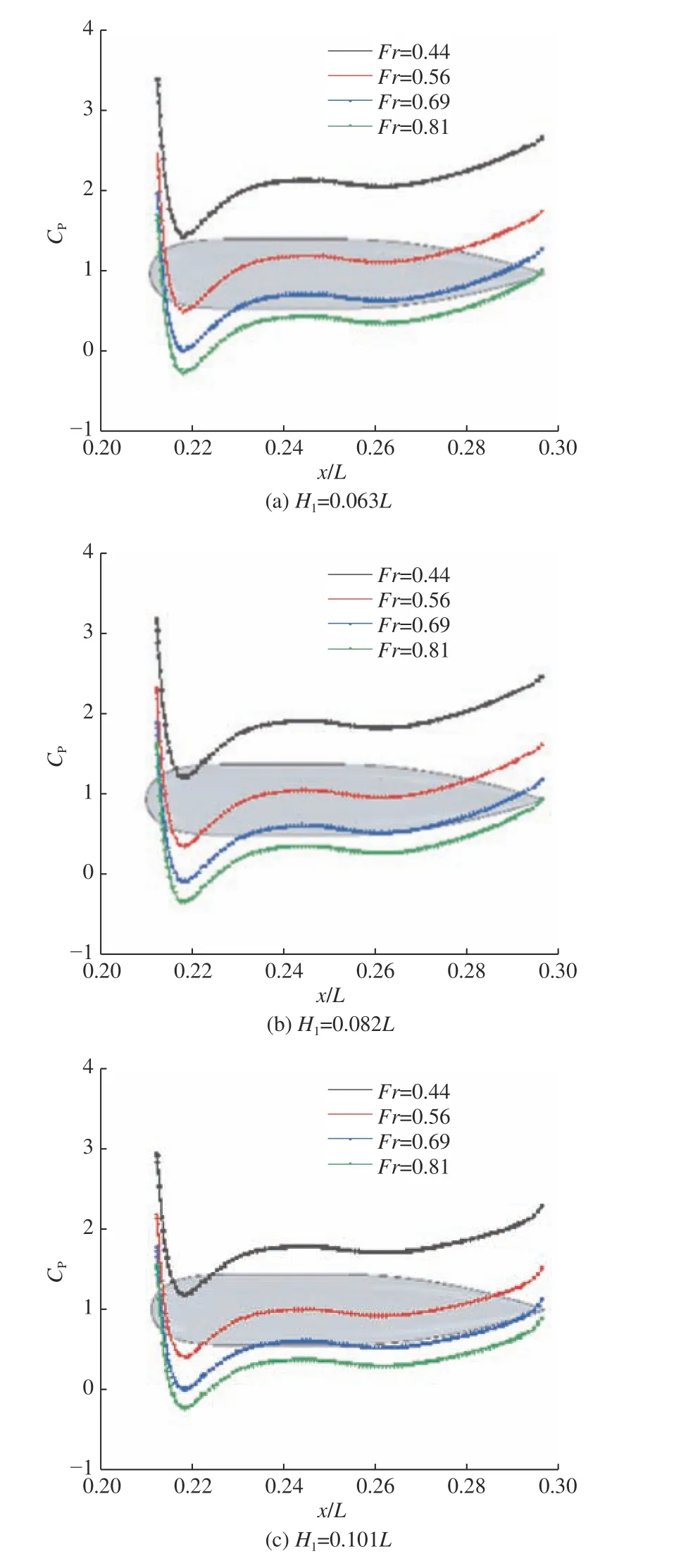
图14 近冰面航行时各弗劳德数下指挥室围壳不同高度截线的Cp 分布对比（d =1.25 m）Fig. 14 The CP distribution of sail transversals at different heights for different Froude numbers when sailing near the ice surface (d =1.25 m)

3.3 潜艇近冰面绕流场分析

3.3.1 潜艇中纵剖面速度场分析

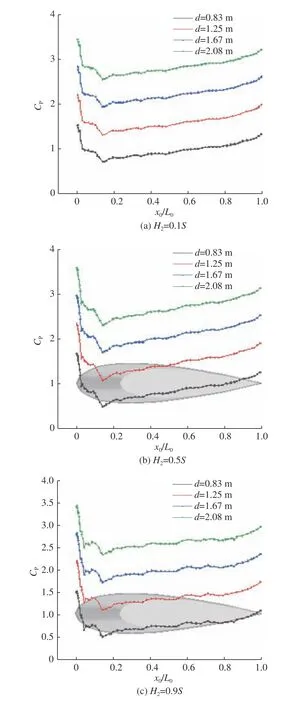
图15 近冰面航行时各潜深下尾翼不同高度截线处Cp 分布对比（Fr=0.56）Fig. 15 The CP distribution of trail transversals at different heights for different submergence depths when sailing near the ice surface (Fr=0.56)

为了直观地说明各参数对艇体周围绕流场的影响，提取了Fr=0.56 时各潜深下的艇体中纵剖面速度场，以及d=1.25 m 时各弗劳德数下的艇体中纵剖面速度场，如图17 和图18 所示。由图17和图18 可以发现，在艇艏前方、围壳后方以及尾翼后方形成了低速高压区，这与潜艇的压阻力密切相关。艇艏前方的流动主要由艇艏驻点控制，由艇艏前端向艏肩处形成顺压梯度，这使得边界层向艏肩处方向逐渐变厚，从而影响艇体的压阻力。指挥室围壳及尾翼处边界层的分离在船体后面产生了复杂的尾流，包括围壳后方的马蹄涡，并在该区域形成了高压区[17]。艇体绕流场的复杂程度沿垂向向上逐渐降低，在围壳周围流场，层次最为丰富。

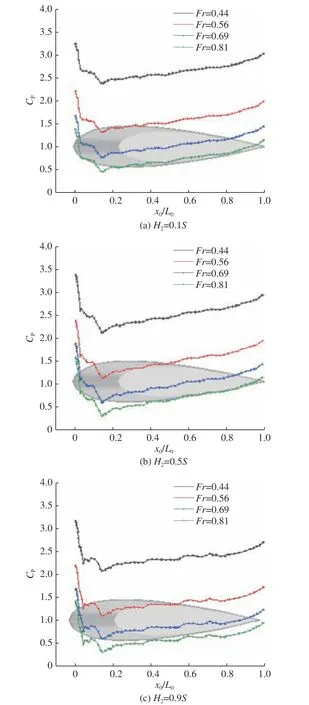
图16 近冰面航行时各弗劳德数下尾翼不同高度截线处Cp 分布对比（d =1.25 m）Fig. 16 The distribution of Cp of trail transversals at different heights for different Froude numbers when sailing near the ice surface (d =1.25 m)

指挥室围壳周围流场复杂的原因是围壳后缘收缩的型线形状，其导致了逆压梯度的形成，为边界层的分离提供了必要条件。而边界层的分离会使背流面的流场变得更加复杂，从而形成一片混乱的尾迹。这也就解释了图17 和图18 所示速度云图中，潜艇指挥室围壳后缘流速较低且流场较为紊乱的原因。

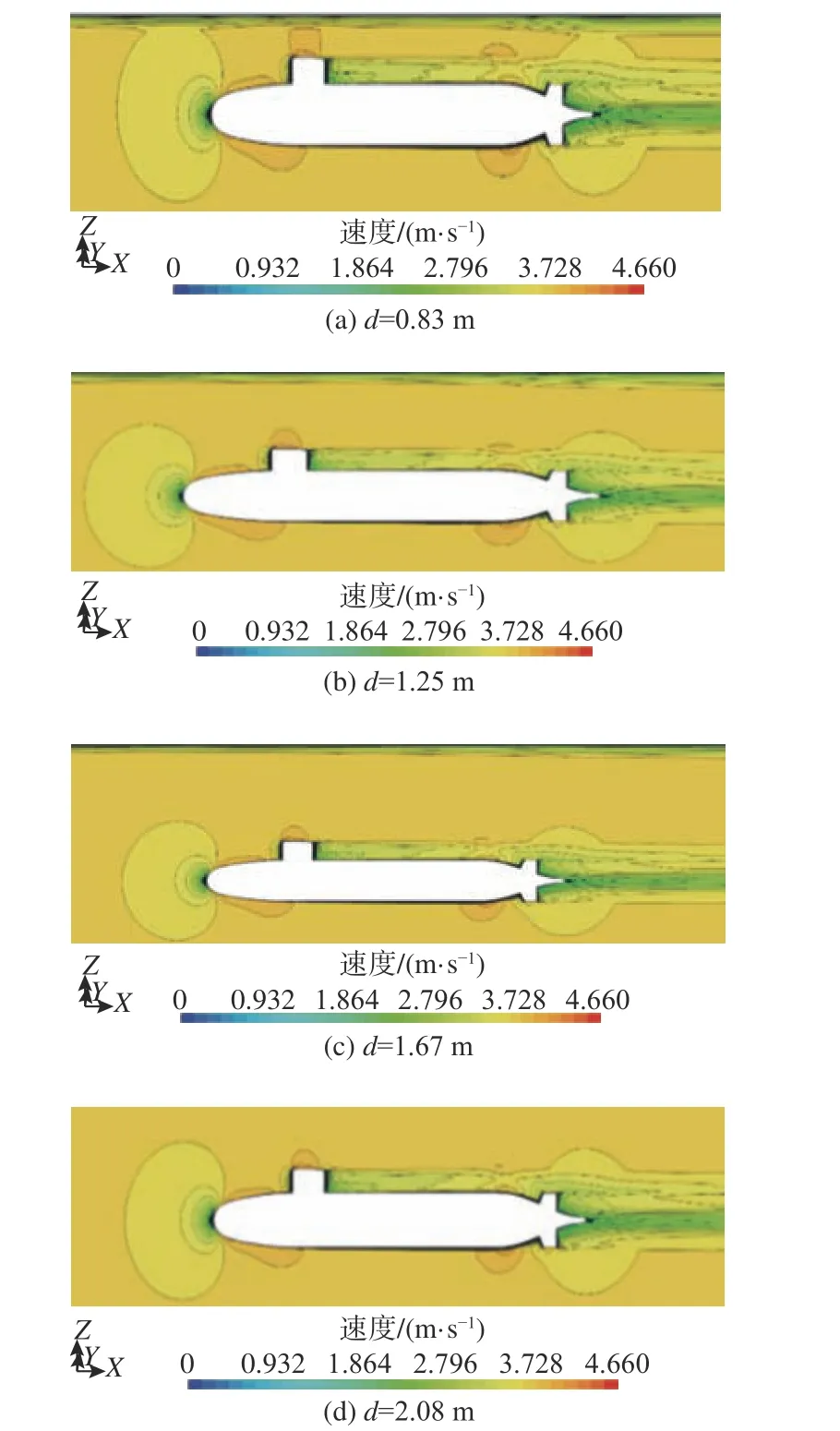
图17 近冰面航行时各潜深下艇体中纵剖面速度场（Fr=0.56）Fig. 17 The velocity distribution of upper submarine mid profile at different submergence depths when sailing near the ice surface (Fr=0.56)

由图17 可以发现，在同一弗劳德数（Fr=0.56）下，艇体近冰面航行（d=0.83 m，即d/D=1.63）时艇周的速度等值线被冰面阻断了。结合图8(b)可以看出，在Fr=0.56 时的各个潜深工况中，d=0.83 m（即d/D=1.63）时CVP略高，在其他3 个较大潜深条件下所得到的CVP几乎相同。这说明潜艇近冰面航行时，在过小潜深（d=0.83 m，d/D=1.63）下，冰面对艇体周围中纵剖面速度场的干扰会使得潜艇的压阻力系数增大。并且在同一弗劳德数下，当d/D>1.63 时，潜深对艇体绕流场的影响可以忽略。

对比图18(a)～图18(d)可以发现，弗劳德数对艇体和冰面的相互作用影响显著。当Fr=0.44～0.81时，由艇体至冰面之间可以观察到明显的由前向后的低、高、低速区，根据伯努利原理，若潜艇近水面航行，相应位置的液面就会因此出现高、低、高的变化，形成明显的波形。而在潜深足够及不存在等值线被冰面阻断的情况下，随着弗劳德数的变化，艇体周围的速度场并不会发生如之前改变潜深时比较明显的变化。由此可以大胆推测，当潜深足够时，航速的增加不会对艇体中纵剖面的速度场分布形态造成影响。

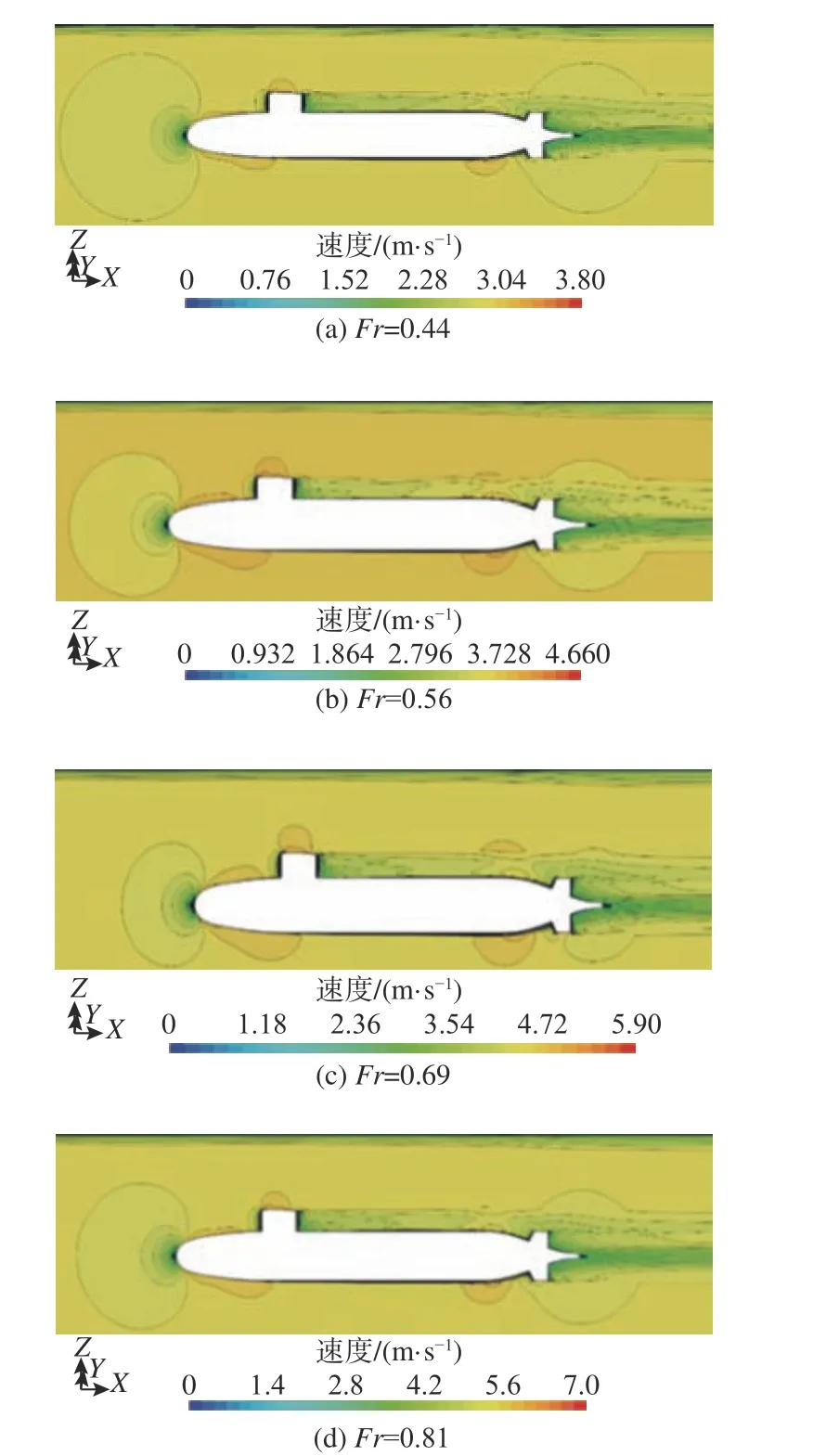
图18 近冰面航行各弗劳德数下艇体中纵剖面速度场（d=1.25 m）Fig. 18 The velocity distribution of upper submarine mid profile for different Froude numbers when sailing near the ice surface (d=1.25 m)

3.3.2 潜艇中纵剖面涡量场分析

由艇体周围的涡量轮廓图和桨盘面处的涡量等值线，可以补充上述航速、潜深对艇体绕流场的理解。涡量为速度的旋度，图19～图20 较好地描述了艇体附近的涡量分布。由于在指挥室围壳后方和尾翼后方出现了界层分离，因而易形成涡，且涡量分布较为密集，这与文献[17-18]中得到的各轴向站位涡量分布规律相符。通过对比图19 和图20可以发现，潜深对艇艉处涡量等值区域范围的影响较大，而艇体航行速度对艇艉涡量等值区域等值线密集度及涡量大小的影响较大。当Fr=0.56，d=2.08 m 时，各轴向站位的涡量分布集中在艇体较小的区域，说明在同一弗劳德数（Fr=0.56）下，冰面对围壳、尾翼后方的旋涡形成有较大影响。而在同一航行深度（d=1.25 m）下，Fr=0.81 时所得到的涡量分布图在旋涡分布面积几乎相同的前提下，在每个站位涡量分布图内的等值线都更为密集，涡量的值也较大，这说明高航速下速度的旋度会相应增大，从而加速边界层分离，使艇体的粘压阻力增大。

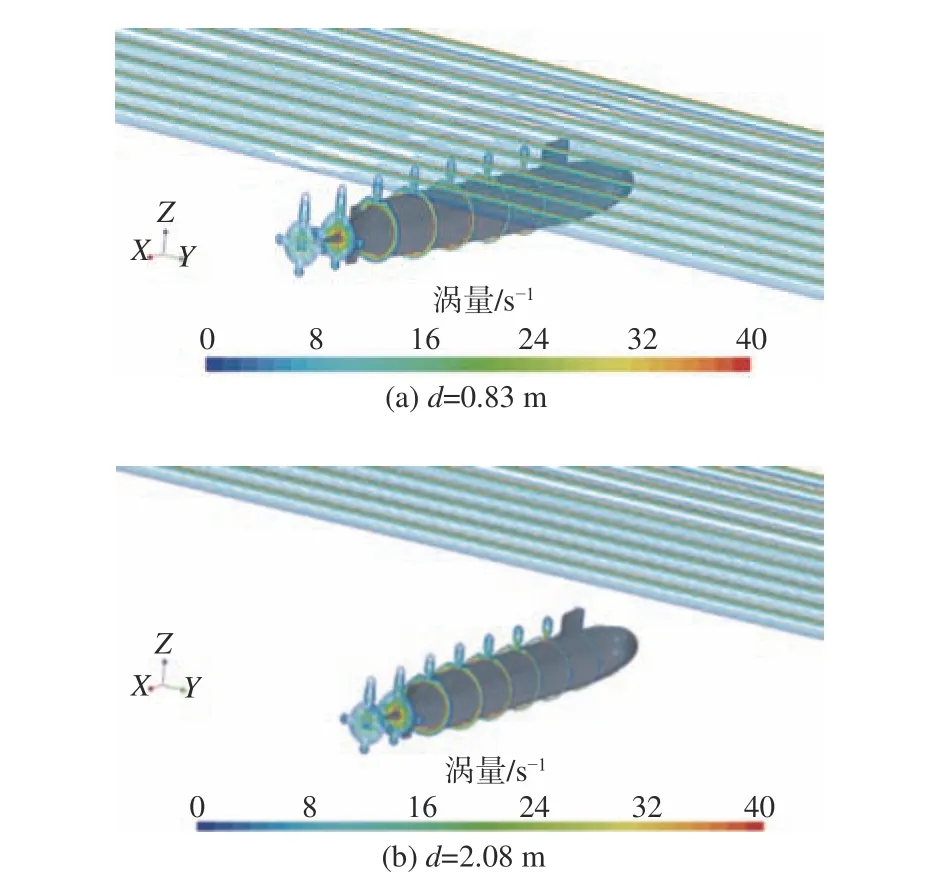
图19 Fr=0.56 时高、低潜深下艇体各轴向站位涡量轮廓图Fig. 19 The vorticity distribution at different axial positions under high/low submergence depth when Fr=0.56

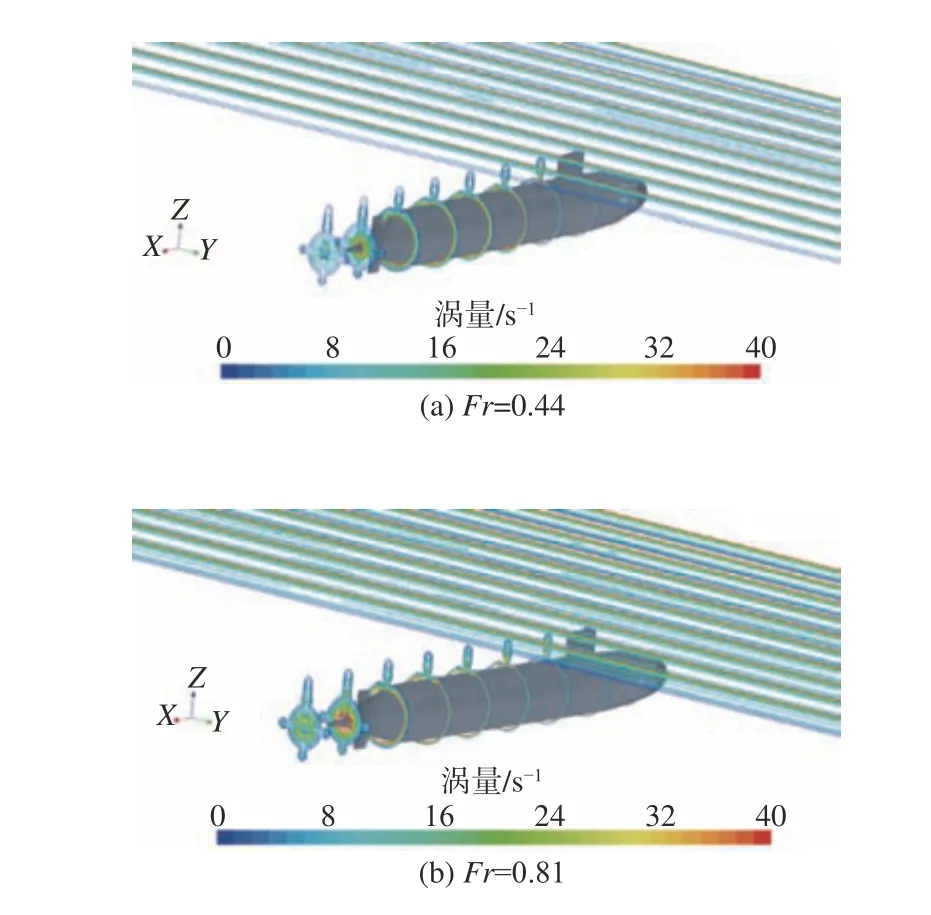
图20 d=1.25 m 时各弗劳德数下的艇体各轴向站位涡量轮廓图Fig. 20 The vortcity distribution at different axial positions for different Froude numbers when d=1.25 m

此外，由图19 和图20 还可以发现，在Suboff潜艇模型近冰面航行情况下，由于对冰面下表面所设的无滑移壁面边界条件，在壁面粘滞力的作用下，在截取艇体轴向各站位的涡量轮廓图时发现冰面下方涡量场的分布较规则；在各工况下，近冰面的涡量场对艇周涡量场未体现出干扰。

4 结 论

为了探究冰面作为边界条件对潜艇航行阻力性能、表面压力系数及绕流场的影响，本文以Suboff 全附体潜艇模型为研究对象，建立了近冰面航行模型，系统计算并分析了潜深和弗劳德数对近冰面航行的阻力和流场特性的影响，主要得出以下结论：

1) 潜艇近冰面航行时，潜艇的总阻力系数CT在同一弗劳德数下随潜深的增加而减小，在同一潜深下随弗劳德数的增加而减小。艇体的摩擦阻力系数CF占据了总阻力系数CT的较大部分，压阻力系数CVP为次要成分。

2) 艇体近冰面航行时，在同一弗劳汝德数下，当d/D>1.63 时，潜深几乎不影响艇体阻力系数。此外，由于没有表面兴波对压阻力的影响，近冰面航行时弗劳德数对总阻力系数的影响较为规律。

3) 艇体在冰面下航行时，在指挥室围壳后缘以及尾翼后缘出现了边界层分离，表面压力系数Cp变化较大。在同一弗劳德数下，各潜深下的Cp沿艇体分布的规律几乎相同。随着潜深的均匀增加，Cp也呈均匀增加的趋势。在同一潜深下，随着弗劳德数的增加，Cp呈指数型下降。

4) 潜艇在近冰面航行时，由于艇体型线的收缩，产生了逆压梯度，从而为边界层分离提供了必要条件，使得围壳后方各站位轴向涡量轮廓等值线更为密集，潜艇近冰面航行时在围壳后缘附近产生的流场沿Z轴正方向的复杂程度较大。并且，计算工况内的弗劳德数对艇体中纵剖面绕流速度场的分布均影响微弱；d/D>1.63 时，潜深对艇体绕流场的影响可以忽略。