基于连续三角模方幂的模糊蕴涵关于三角模与三角余模的分配方程

付伊嘉, 周红军

(陕西师范大学数学与统计学院，西安 710119)

0 引言

模糊蕴涵在包括模糊形态学、图像处理、词语计算、数据挖掘、粗糙集、模糊关系方程等在内的诸多模糊数学分支中扮演着重要的角色[1–7]。因此，很多学者致力于模糊蕴涵的研究，并且促进了模糊蕴涵的快速发展。根据构造方法，模糊蕴涵可分为(S,N)-蕴涵、R-蕴涵、QL-蕴涵、Yager 蕴涵以及序和蕴涵[8–10]。最近，文献[11–14]中基于连续三角模的幂提出了T-幂蕴涵。文献[15–17]对这类蕴涵的一些重要性质做了深入研究，T-幂蕴涵的重要性在于其可以满足一些特殊的性质，这使得它在近似推理的应用中是不可或缺的，本文也将说明T- 幂蕴涵不同于其他各类模糊蕴涵。

各类模糊蕴涵关于三角模和三角余模的分配方程是重要的研究方向，主要包括如下四类分配方程，它们分别是二值命题逻辑中相应重言式的模糊化，在刻画逻辑代数的代数结构和解决模糊系统中推理规则爆炸问题中均起着重要作用[18–19]

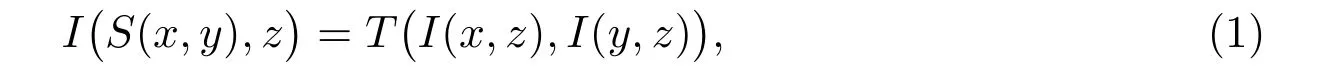
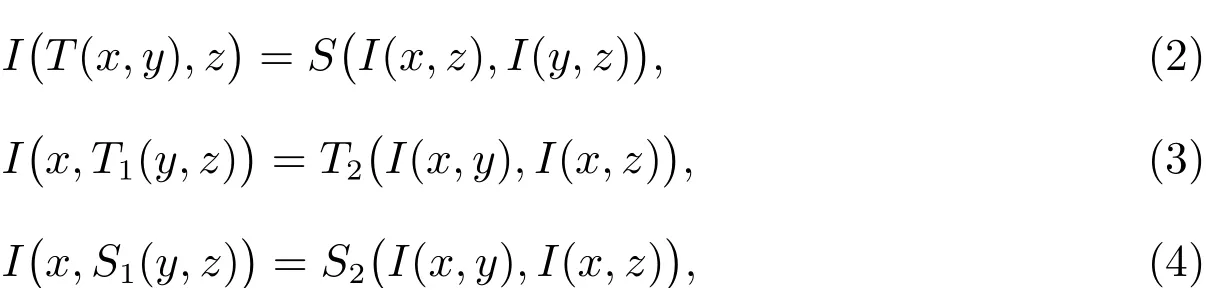
其中I是模糊蕴涵，T、T1、T2是三角模，S、S1、S2是三角余模。目前主要研究成果有：

1) 文献[20]给出了当I是(S,N)-蕴涵、R-蕴涵、QL-蕴涵时，分配方程(1)～(4)的解；

2) 文献[9]给出了序和蕴涵关于三角模和三角余模的四类分配方程的解；

3) 文献[21]研究了四类分配方程在I取一些特殊的R-蕴涵和S-蕴涵时，T与S的结构刻画；

4) 文献[22]研究了当I是由严格三角模生成的R-蕴涵时，分配方程I(x,S(y,z)) =S(I(x,y),I(x,z))的求解问题；

5) 文献[23–24]分别将四类分配方程中的三角模T和三角余模S推广到可表示一致模的情形，当T和S都是给定的可表示一致模时，刻画了模糊蕴涵I满足式(1)和式(2)时的结构；他们也刻画了当T1=T2都是严格三角模时，分配方程(3)的求解问题，并且研究了当S1和S2都是幂零三角余模或者严格三角余模时，模糊蕴涵I满足(4)式时的结构。

此外，关于聚合算子的分配方程也得到大量的研究，文献[25–26]研究了分配方程关于一致模和聚合算子的求解问题，文献[27]研究了分配性方程关于幂等一致模的求解问题.

本文研究T-幂蕴涵关于一般三角模和三角余模的四类分配方程成立的充要条件。论文内容安排如下：第1 节回顾本文需要的预备知识，包括三角模、三角余模、模糊蕴涵、T-幂蕴涵、模糊否定等。第2 节给出T-幂蕴涵关于一般三角模和三角余模的四类分配方程成立的充要条件。第3 节讨论T-幂蕴涵与其他已知模糊蕴涵的关系。第4 节对本文作以简要总结并且对未来工作进行展望。

1 预备知识

为便于阅读，下面回顾本文中用到的一些基本概念和性质。

定义1[28]称二元函数T: [0,1]2→[0,1]是三角模，若T满足交换律与结合律，关于两个变元单调不减，并且以1 为单位。

表1 给出了几种常用的三角模。

表1 常用的三角模

若三角模T满足，对任意的x ∈[0,1], T(x,x)=x，则T=TM。

定义2[28]称二元函数S:[0,1]2→[0,1]是三角余模，若S满足交换律与结合律，关于两个变元单调不减，并且以0 为单位。

表2 给出了几个常用的三角余模。

表2 常用的三角余模

若三角余模S满足，对任意的x ∈[0,1], S(x,x)=x，则S=SM。

定义3[29]称二元函数I:[0,1]2→[0,1]是模糊蕴涵，若对于任意x,y,z ∈[0,1]，I满足以下条件：

(I1) 当x ≤y时，I(y,z)≤I(x,z)；

(I2) 当y ≤z时，I(x,y)≤I(x,z)；

(I3)I(0,0)=1；

(I4)I(1,1)=1；

(I5)I(1,0)=0。

全体模糊蕴涵之集记为FI。从以上定义知，任一模糊蕴涵I满足以下两条性质，分别称为左边界条件和右边界条件：

(LB)I(0,y)=1, y ∈[0,1]；

(RB)I(x,1)=1, x ∈[0,1]。

定义4[28]称一元函数N: [0,1]→[0,1]是模糊否定，若N(0) = 1, N(1) = 0，并且N是单调不增的。

1) 称模糊否定N是标准模糊否定，若对于任意x ∈[0,1], N(x) = 1-x，记为N=NC。

2) 令

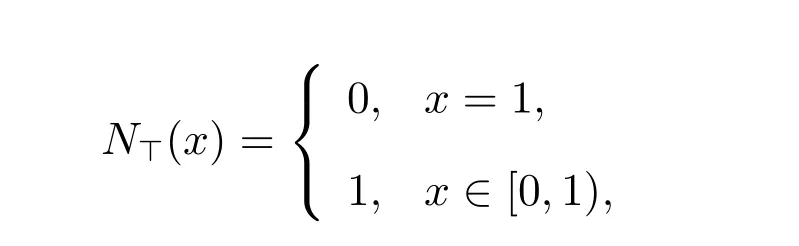
则N⊤是模糊否定，且N⊤是最大的模糊否定。

定义5[30]设I是模糊蕴涵，T是三角模，N是模糊否定，称I满足：

1) 单位元性质(NP)，若对于任意y ∈[0,1]，有I(1,y)=y；

2) 置换性质(EP)，若对于任意x,y,z ∈[0,1]，有I(x,I(y,z))=I(y,I(x,z))；

3) 恒等性质(IP)，若对于任意x ∈[0,1]，有I(x,x)=1；

4) 序性质(OP)，若对于任意x,y ∈[0,1], I(x,y)=1 当且仅当x ≤y；

5) 关于N的逆否性质(CP(N))，若对任意x,y ∈[0,1]，有I(x,y)=I(N(y),N(x))；

6)T的输入原则(LIT)，若对于任意x,y,z ∈[0,1]，有I(T(x,y),z)=I(x,I(y,z))；

7)T传递性，若对于任意x,y,z ∈[0,1]，有T(I(x,y),I(y,z))≤I(x,z)。

设T是连续三角模，根据T的连续性和结合性，可以用通常的递归方式定义元素x ∈[0,1]基于三角模T的整数幂

定理1[29]设T:[0,1]2→[0,1]是二元函数，则以下两条等价：

(i)T是连续的阿基米德三角模；

(ii)T有连续的加法生成子t，即存在一个满足t(1) = 0 的连续且严格单调递减的函数t: [0,1]→[0,∞]，使得对于任意x,y ∈[0,1]，有T(x,y) =t-1(min((t(x)+t(y)),t(0))。三角模的加法生成子在相差正常数倍的意义下是唯一的。

定理2[29]设T是连续的阿基米德三角模，t:[0,1]→[0,∞]是T的加法生成子，则：

1)T是严格三角模，当且仅当t(0)=∞；

2)T是幂零三角模，当且仅当t(0)＜∞。

引理1[17]设T是连续三角模，IT是由T生成的T-幂蕴涵。

1) 若T=TM，则

其中0＜a ＜1。

4) 若T=TL，则

为便于第3 节说明T-幂蕴涵不同于其他已有各类模糊蕴涵，这里再回忆其他各类模糊蕴涵的定义。

定义9[28]称二元函数I: [0,1]2→[0,1]是(S,N)-蕴涵，若存在三角余模S和模糊否定N，使得对于任意x,y ∈[0,1], I(x,y) =S(N(x),y)。为明确起见，将上述I记为IS,N。如果N是强模糊否定，那么称I为强模糊蕴涵或者S-蕴涵。

定义10[28]称二元函数I: [0,1]2→[0,1]是QL-蕴涵，若存在三角模模T，三角余模S和模糊否定N，使得对于任意x,y ∈[0,1], I(x,y) =S(N(x),T(x,y))。为明确起见，将上述I记为IT,S,N。

定义11[28]称二元函数I: [0,1]2→[0,1]是R-蕴涵，若存在三角模T，使得对于任意x,y ∈[0,1], I(x,y)=sup{t ∈[0,1]|T(x,t)≤y}。为明确起见，将上述I记为IT。

2 T-幂蕴涵的分配方程

由文献[29]中7.2 节可知，若模糊蕴涵I满足(NP)，那么I满足分配方程(1)～(4)的充要条件分别是对应分配方程中的T=TM, S=SM。f-蕴涵，g-蕴涵，(S,N)-蕴涵，QL-蕴涵以及R-蕴涵都满足(NP)，然而T-幂蕴涵不满足(NP)，因此，T-幂蕴涵与其他已知模糊蕴涵四类分配方程成立的充要条件的证明方法是不同的。文献[29]仅仅给出了f-蕴涵、g-蕴涵、(S,N)-蕴涵、QL-蕴涵以及R-蕴涵关于三角模和三角余模的四类分配方程成立的充要条件，本节将完善文献[29]的7.2 节关于模糊蕴涵分配方程的内容，给出T-幂蕴涵关于一般三角模和三角余模的四类分配方程成立的充要条件。

2.1 分配方程(1)

定理3 设T是三角模，S是三角余模，ITM是由TM生成的T-幂蕴涵，则(T,S,ITM)满足(1)式，当且仅当S=SM。

证明 =⇒设(T,S,ITM)满足(1)式，x ∈[0,1]，则由(1)式，可得

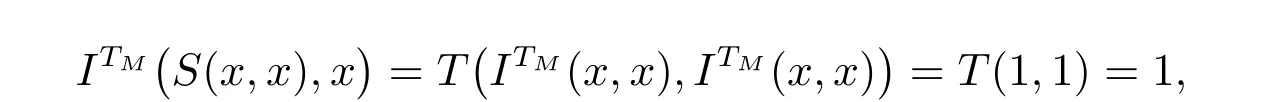
所以S(x,x)≤x。由于S是三角余模，可知S(x,x)≥x，因此，S(x,x) =x，那么S=SM。

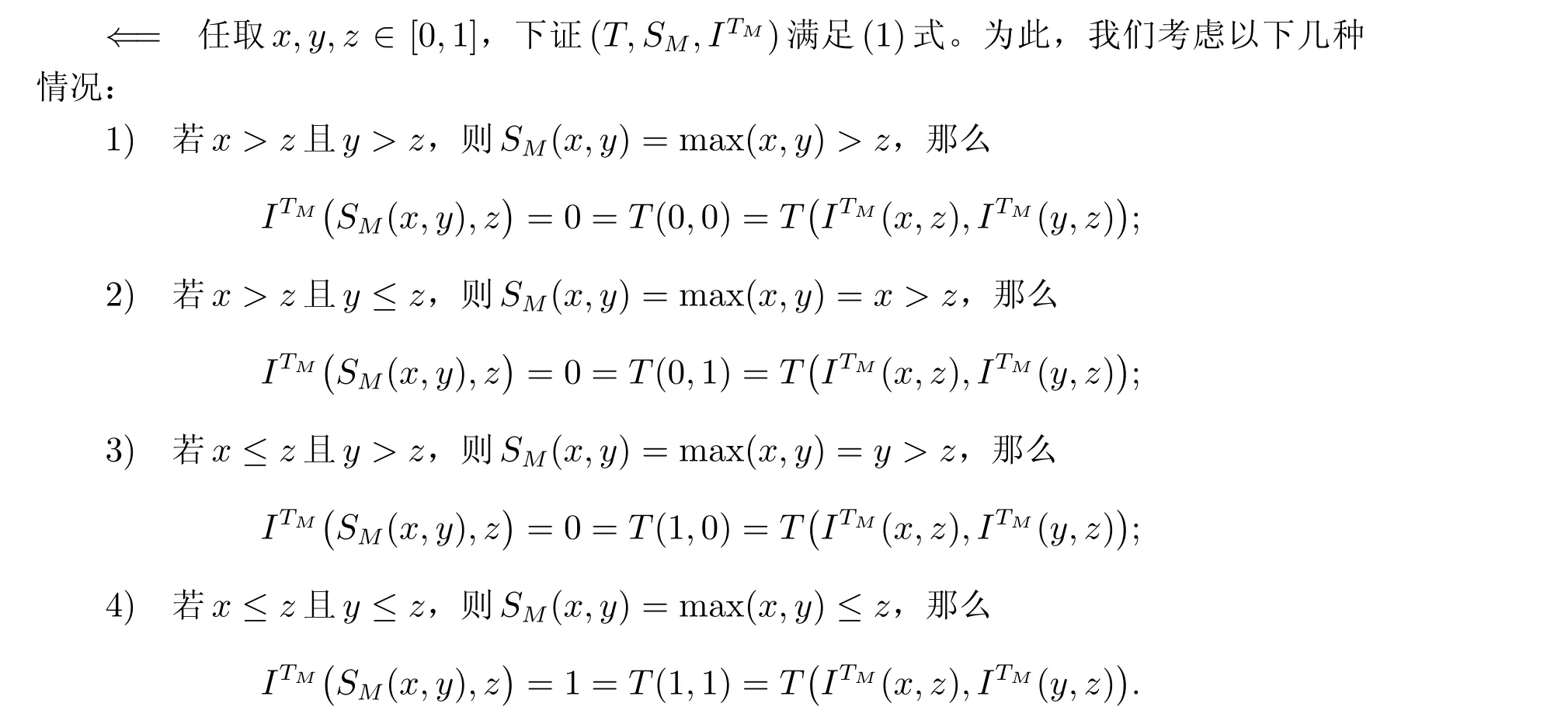
综上，证得(T,SM,ITM)满足(1)式。

定理4 设T*是三角模，S是三角余模，T是连续阿基米德三角模，IT是由T生成的T-幂蕴涵，则(T*,S,IT)满足(1)式，当且仅当T*=TM, S=SM。

证明 =⇒设t是T的加法生成子，(T*,S,IT)满足(1)式，x ∈[0,1]，则由(1)式，可得

综上证得(TM,SM,IT)满足(1)式。

例1 设T是三角模，S是三角余模，ITP是由TP生成的T-幂蕴涵，ITL是由TL生成的T-幂蕴涵。由于TP, TL是连续的阿基米德三角模，所以由定理4 可知：

(i) (T,S,ITP)满足(1)式，当且仅当T=TM, S=SM；(ii) (T,S,ITL)满足(1)式，当且仅当T=TM, S=SM。

定理5 设T= (〈aα,bα,Tα〉)α∈A是连续的序和三角模，其中Tα是连续的阿基米德三角模，α ∈A。设IT是由T生成的T-幂蕴涵，T*是三角模，S是三角余模，则(T*,S,IT)满足(1)式，当且仅当T*=TM, S=SM。

证明 =⇒假设(T*,S,IT)满足(1)式，对于任意α ∈A, tα是Tα的加法生成子。任取x ∈[0,1]，由(1)式，可得

因此IT(SM(x,y),z)=1，且TM(IT(x,z),IT(y,z))=TM(1,1)=1；否则

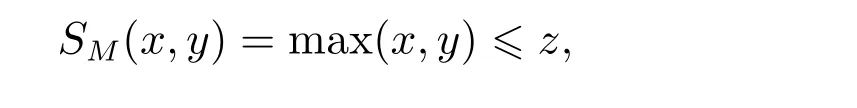
从而IT(SM(x,y),z)=1，且TM(IT(x,z),IT(y,z))=TM(1,1)=1；

② 若x ≤ z且y ＞ z，则SM(x,y) = max(x,y) =y ＞ z，并且IT(x,z) =1, IT(y,z)=0。因此IT(SM(x,y),z)=0，且TM(IT(x,z),IT(y,z))=TM(1,0)=0；

③ 若y ≤z且x ＞z，则与上述情况类似；

④ 若x ＞z且y ＞z，则SM(x,y) = max(x,y)＞z，并且IT(x,z) =IT(y,z) =0。因此IT(SM(x,y),z)=0，且TM(IT(x,z),IT(y,z))=TM(0,0)=0；

2) 存在α0∈A，使得z ∈[aα0,bα0]，根据x, y与区间[aα0,bα0]之间的大小关系，再讨论以下五种情况：

① 若x,y/∈∪α0∈A[aα0,bα0]，则根据x, y, aα0, bα0之间的大小关系，再讨论以下四种子情况：

(a) 若x ≤aα0，并且y ≤aα0，则SM(x,y)≤aα0≤z，从而IT(x,z)=IT(y,z)=1，因此IT(SM(x,y),z)=1，并且TM(IT(x,z),IT(y,z))=TM(1,1)=1；

(b) 若x ＞bα0，并且y ＞bα0，则SM(x,y)＞bα0≥z，从而IT(SM(x,y),z)=0，并且TM(IT(x,z),IT(y,z))=TM(0,0)=0；

(c) 若y ≤aα0，并且x ＞bα0，则IT(SM(x,y),z)=0，并且TM(IT(x,z),IT(y,z))=TM(0,1)=0；

(d) 若x ≤ aα0，并且y ＞ bα0，则与上述子情况类似，仍有(TM,SM,IT)满足(1)式；

②x ∈[aα0,bα0]且y/∈[aα0,bα0]，再讨论以下两种子情况：

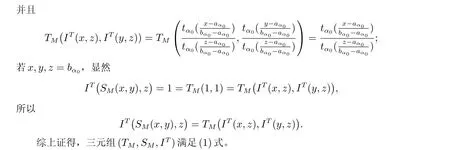
2.2 分配方程(2)

命题1[29]设二元函数I:[0,1]2→[0,1]，则以下两条等价：

(i)I关于第一变元单调不增，即I满足(I1)；

(ii)I满足分配方程I(min(x,y),z)=max(I(x,z),I(y,z))。

注1 由命题1 可知，当T=TM, S=SM时，对于任意模糊蕴涵I，三元组(TM,SM,I)都满足(2)式，从而(TM,SM,IT)也满足(2)式。

接下来刻画当T*和IT都是固定的，三元组(T*,S,IT)满足(2)式时三角余模S的结构。下面的命题是自明的。

命题2 设T*=TM是三角模，S是三角余模，则：

(i) 若ITM是由TM生成的T-幂蕴涵，则三元组(T*,S,ITM)都满足(2)式；

(ii) 设T是连续阿基米德三角模，IT是由T生成的T-幂蕴涵，则(T*,S,IT)满足(2)式，当且仅当S=SM；

(iii) 设T= (〈aα,bα,Tα〉)α∈A是连续的序和三角模，IT是由T生成的T-幂蕴涵，则(T*,S,IT)满足(2)式，当且仅当S=SM。

定理6 设S是三角余模，T是连续阿基米德三角模，IT是由T生成的T-幂蕴涵，则(T,S,IT)满足(2)式，当且仅当S=SL。

显然成立。综上证得三元组(T,SL,IT)满足(2)式。

例2 设S是三角余模，IT是由连续三角模T生成的T-幂蕴涵。由于TP、TL是连续的阿基米德三角模，所以由定理6 可知：

(i) 若T=TP，则(T,S,IT)满足(2)式，当且仅当S=SL；

若x,y,z=bα，显然

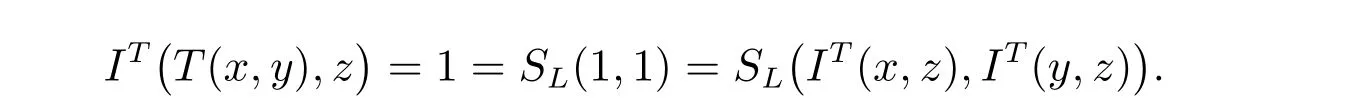
若x,y,z/∈∪α∈A[aα,bα]，易证(T,SL,IT)满足(2)式。综上证得(T,SL,IT)满足(2)式。

推论1 设S是三角余模，T*是三角模，IT是由连续的三角模T生成的T-幂蕴涵，则有：

(i) 若T*=TP, T=TL或T*=TL, T=TP，则不存在S，使得三元组(T*,S,IT)满足(2)式；

(ii) 若T*是连续的阿基米德三角模，T是连续的非平凡序和三角模，则不存在S，使得三元组(T*,S,IT)满足(2)式；

(iii) 若T*是连续的非平凡序和三角模，T是连续的阿基米德三角模，则不存在S，使得三元组(T*,S,IT)满足(2)式。

证明 (i) 若T*=TP, T=TL，假设存在S，使得三元组(TP,S,ITL)满足(2)式。若x ＞z, y ＞z且TP(x,y)＞z，则

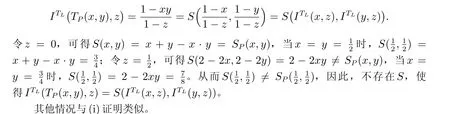
2.3 分配方程(3)

所以T2(λ,λ)=λ；若x,y=bα，显然T2(1,1)=1；若x,y/∈∪α∈A[aα,bα]，显然T2(0,0)=0。综上证得T2=TM。

⇐= 下证(TM,TM,IT)满足(3)式。根据元素x与区间[aα,bα]的关系，分为两种情况：x/∈[aα,bα]和x ∈[aα,bα]。

1) 若对于任意α ∈A, x/∈[aα,bα]，根据x, y, z之间的大小关系，再讨论以下四种情况：

① 若x ≤y且x ≤z，如果存在α0∈A，使得y,z ∈[aα0,bα0]，可知TM(y,z)≥aα0＞x，因此IT(x,TM(y,z)) = 1，且TM(IT(x,y),IT(x,z)) =TM(1,1) = 1；否则TM(y,z) = min(y,z)≥x，因此IT(x,TM(y,z)) = 1，且TM(IT(x,y),IT(x,z)) =TM(1,1)=1；

② 若x ≤z且x ＞y，则TM(y,z) = min(y,z) =y ＜x，因此IT(x,TM(y,z)) =0，且TM(IT(x,y),IT(x,z))=TM(0,1)=0；

③ 若x ≤y且x ＞z，则与上述情况类似；

④ 若x ＞y且x ＞z，则TM(y,z) = min(y,z)＜x，因此IT(x,TM(y,z)) = 0，且TM(IT(x,y),IT(x,z))=TM(0,0)=0。

2.4 分配方程(4)

定理11 设I是满足(OP)的模糊蕴涵，S是三角余模，并且I满足I(x,S(y,z)) =S(I(x,y),I(x,z))，那么三角余模S是幂等的，或不是正的。证明 若S是幂等的，则S=SM，任何模糊蕴涵满足

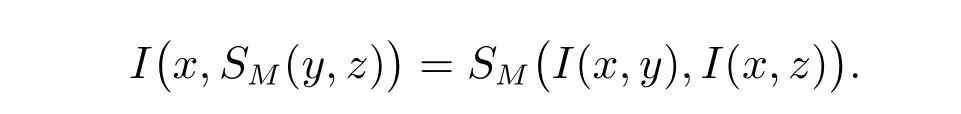
另一方面，令S/=SM，那么存在y ∈(0,1)，使得S(y,y)＞y，因为对于任意x ∈(y,S(y,y))，I满足I(x,S(y,z)) =S(I(x,y),I(x,z))，通过(OP)可得I(x,y) =y0＜1，并且

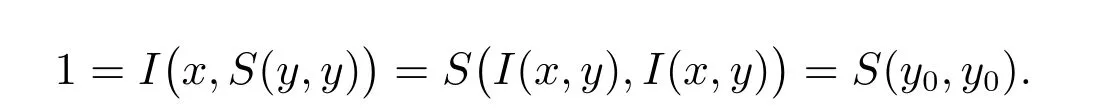
因此，三角余模S不是正的。

分配方程(3)式和(4)式中，由于三角余模T和三角模S是对偶的，因此，由定理8 和定理9 可得以下两条定理。

定理12 设S1, S2是连续的三角余模，ITM是由TM生成的T-幂蕴涵，则(S1,S2,ITM)满足(4)式，当且仅当S1=SM。

定理13 设S1, S2是连续的三角余模，T是幂零三角模，IT是由T生成的T-幂蕴涵，则(S1,S2,IT)满足(4)式，当且仅当S1=S2=SM。

注2 若定理13 中的T是严格三角模且有连续的加法生成子t，则T是正的。由定理11 可知，S2是T的对偶三角余模，因此，不存在三角余模S1，使得三元组(S1,S2,IT)满足(4)式。

例4 设S1, S2是连续的三角余模，ITL是由TL生成的T-幂蕴涵，由于TL是幂零三角模，由定理13 可知(S1,S2,ITL)满足(4)式，当且仅当S1=S2=SM。

定理14 设T= (〈aα,bα,Tα〉)α∈A是连续的序和三角模，IT是由T生成的T-幂蕴涵，S1, S2是三角余模，则(S1,S2,IT)满足(4)式，当且仅当S1=S2=SM。

证明 证明过程和定理10 类似。

称等式(p ∧q)→r ≡(p →(q →r))为输入定律，它是经典逻辑中的重言式。如上重言式的模糊化由下式给出

其中I是模糊蕴涵，T是三角模[20]。

注3[20]如果模糊蕴涵I关于任何三角模T满足(6)，通过T的可交换性，那么I满足(EP)。因为T-幂蕴涵不满足(EP)，那么它一定不满足(6)。

3 T-幂蕴涵与几类模糊蕴涵的关系

下面，我们研究T-幂蕴涵与f-蕴涵、g-蕴涵、(S,N)-蕴涵、QL-蕴涵，以及R-蕴涵的关系。

命题3 设f是f-生成子，且f(0)=∞，If是f-生成子生成的f-蕴涵，则If一定不是T-幂蕴涵。

证明 假设存在连续三角模T满足If(x,y)=IT(x,y)，则对于任意x,y ∈[0,1]，有

由于f(0) =∞，当x=y= 0 时，有f-1(0·f(0)) =f-1(∞) = 0。然而IT(x,y) =IT(0,0)=1，矛盾！所以If一定不是T-幂蕴涵。

命题4 设g是g-生成子，Ig是g-生成子生成的g-蕴涵，则Ig一定不是T-幂蕴涵。证明 假设存在连续三角模T，使得Ig(x,y) =IT(x,y)，则对于任意的x,y ∈[0,1]，有

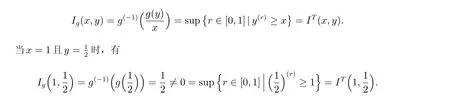
矛盾！因此，Ig一定不是T-幂蕴涵。

命题5 设S是三角余模，N是模糊否定，I是由S和N生成的(S,N)-蕴涵，则I一定不是T-幂蕴涵。

证明 设存在三角模S和模糊蕴涵N，使得IS,N=IT，则对于任意x,y ∈[0,1]，有

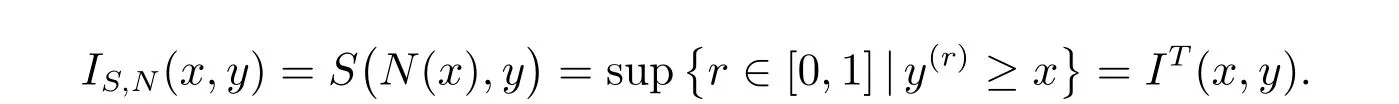
取x= 1, y ∈(0,1)，则由文献[15]中的命题8 知，IS,N(1,y) =y/= 0 =IT(1,y)。因此，(S,N)-蕴涵一定不是T-幂蕴涵。

命题6 设T是三角模，S是三角余模，N是模糊否定，I是由T、S、N构成的QL-蕴涵，则I一定不是T-幂蕴涵。

证明 由文献[28]中例2.6.4 给出下表3，在以下七种情况下，T、S以及N构成的QL-蕴涵都不是T-幂蕴涵。

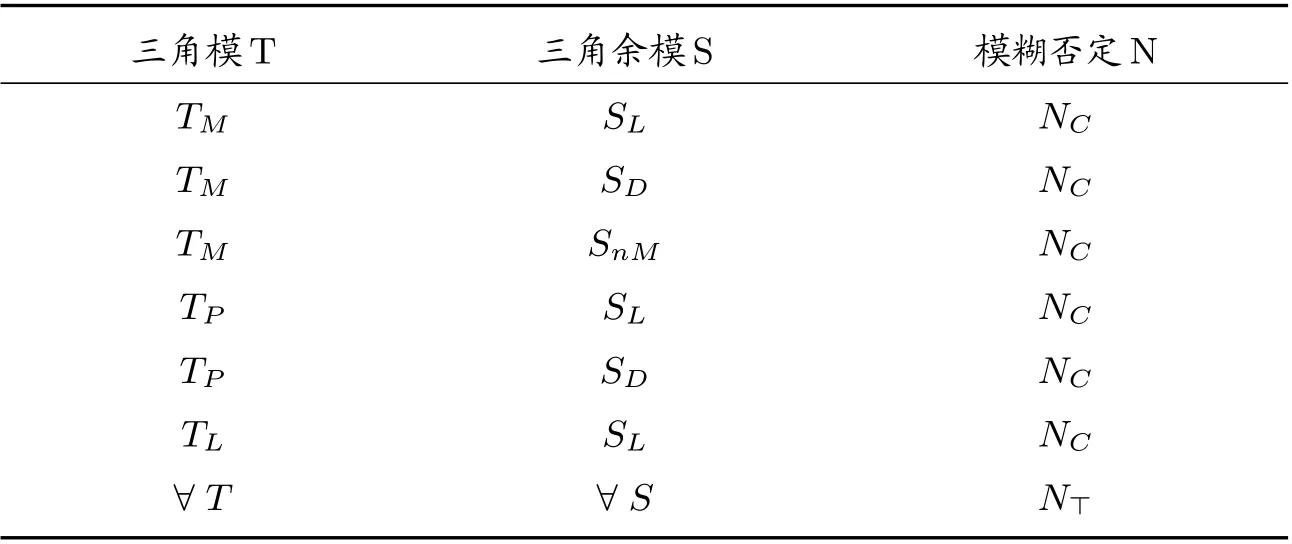
表3 常用QL-蕴涵中的T, S 与N

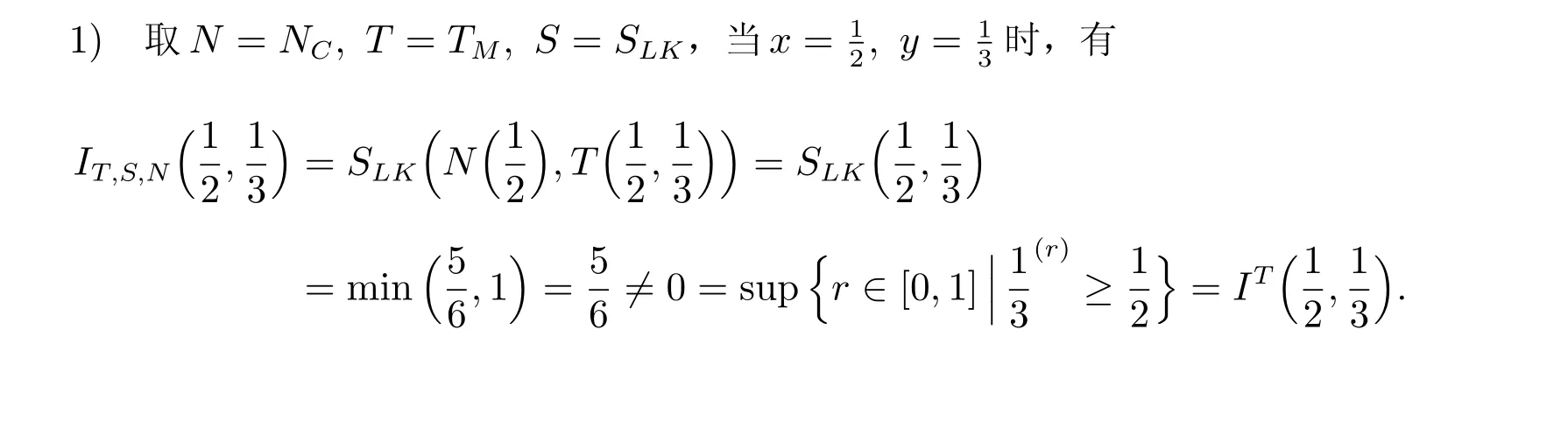
4 结束语

本文较系统研究了T-幂蕴涵关于一般三角模和三角余模的四类分配方程成立的充分必要条件，并说明了T-幂蕴涵是新的一类模糊蕴涵。今后，将关注由一致模等其他聚合算子如何利用方幂生成模糊蕴涵，并研究相应模糊蕴涵关于一致模的分配性方程等。