二维抛物型奇异摄动问题的移动网格方法

周 琴

(湖南涉外经济学院信息与机电工程学院，长沙 410205)

0 引言

二维抛物型奇异摄动问题在自然科学、工程等领域有着广泛的应用背景，它可以描述物质扩散时的浓度变化规律，土壤力学中的渗流问题等等。该类问题的解通常在局部范围内会产生剧烈的变化，在均匀网格上获取数值解不能很好地逼近实际问题。目前求解奇异摄动问题的非均匀网格方法主要有自适应移动网格方法[?,?,?,?]和层适应网格方法[5–6]等。其中自适应移动网格方法通过网格的迭代变化使解变化较大的区域集中较多的网格点，能较好地反映解的性质。

奇异摄动问题的自适应移动网格方法研究中，关于二维问题的研究成果相对较少。文献[?]针对一维奇异摄动对流扩散方程组问题，利用有限差分方法，提出了基于等弧长分布的自适应移动网格方法，并给出了一阶后验误差估计。文献[2–3]分别对一维奇异摄动时变对流扩散问题和一阶奇异摄动初值问题进行分析，建立了基于等分布弧长的移动网格方法。文献[?]提出将适合问题的层适应网格作为初始网格来进行网格移动，比较了两种移动网格方法。文献[7–8]针对一阶的双曲守恒律方程提出了基于等分布原理的移动网格方法。文献[?,?,?,?,?]研究了自适应移动网格方法在流体力学等问题中的应用.

我们考虑一类含源项二维抛物型奇异摄动问题其中0＜ε ≪1, Ω=[a1,b1]×[a2,b2]。函数f(x,y,t)为已知的源汇函数，设它满足一定的正则性条件。本文将提出计算问题(??)的自适应移动网格算法，并给出两个算例的数值实验结果。

1 数值格式

本节构造移动网格上求解问题(??)的数值格式。设某时刻物理平面上网格分布为{(xj,k,yj,k)}, j= 0,1,··· ,N, k= 0,1,··· ,M，对应数值解为{uj,k}。由于自适应移动网格方法中的网格是迭代变化的，网格移动后产生的新网格为不规则的四边形网格，不适用常规的数值方法作数值计算。因此，在某个时间层迭代的最终网格形成后，需要将不规则的四边形网格转化为计算平面上均匀分布的网格，以便于后续计算。记计算平面上均匀分布的网格为{(ξj,ηk)}, j= 0,1,··· ,N, k= 0,1,··· ,M。在计算过程中，计算平面上的网格总是保持不变,用来辅助求解问题。记

2 网格迭代方法和解的重新分布

3 移动网格算法和数值实验

基于前文构造的数值格式及网格迭代时解的重新分布方法，下面给出移动网格方法求解模型方程(??)的算法。

第4 步 如果tm+1≤T，令m=m+1，转第2 步；否则，算法终止，得到T时刻的数值解。

下面根据上述算法对两个算例进行数值实验。

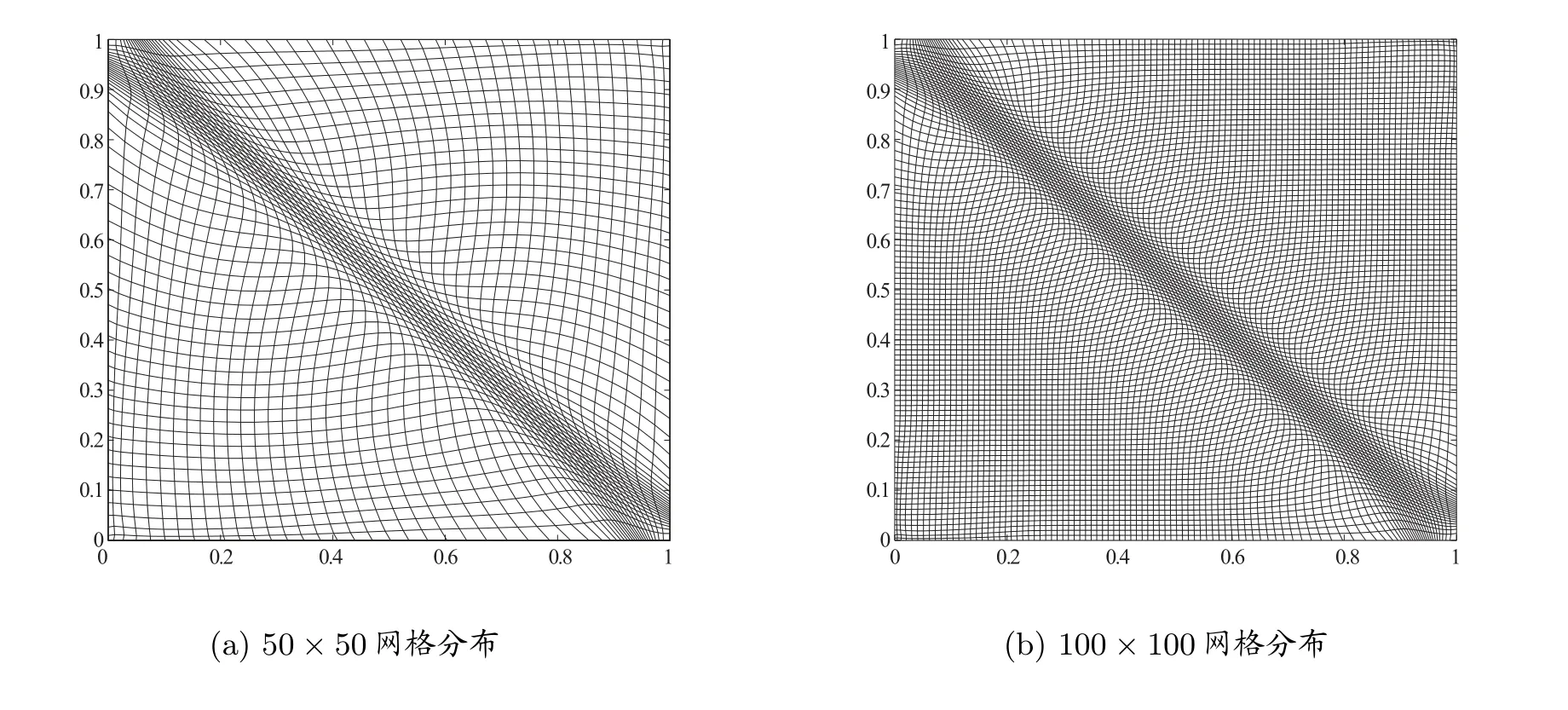
图1 t=0.5, ε=0.001 时，例1 的自适应移动网格分布

图2 为例2 中t= 0.2, ε2= 0.0001 时，空间网格数分别为50×50 和100×100 节点的自适应网格分布。该问题的解在边界x=1, y=1 附近变化比较剧烈，由图2 可见自适应网格在该边界层比较集中。这些结果充分说明了对于二维抛物型奇异摄动问题，通过移动网格方法求解能自适应地进行局部加密，能较好地体现解在局部区域的特性。

图2 t=0.2, ε2 =0.0001 时，例2 的自适应移动网格分布

来度量。图3(a)和图3(b)分别为50×50 空间网格点的自适应移动网格和均匀网格上求解例1的误差图像(取t=0.5, ε=0.001 时)。为了便于比较，图3(a)选取的网格节点为计算平面上均匀分布的网格，该网格是由物理平面上的不规则网格经过坐标变换映射产生的。比较两个图象可以看出，移动网格上求解的精度优于均匀网格上求解的精度。

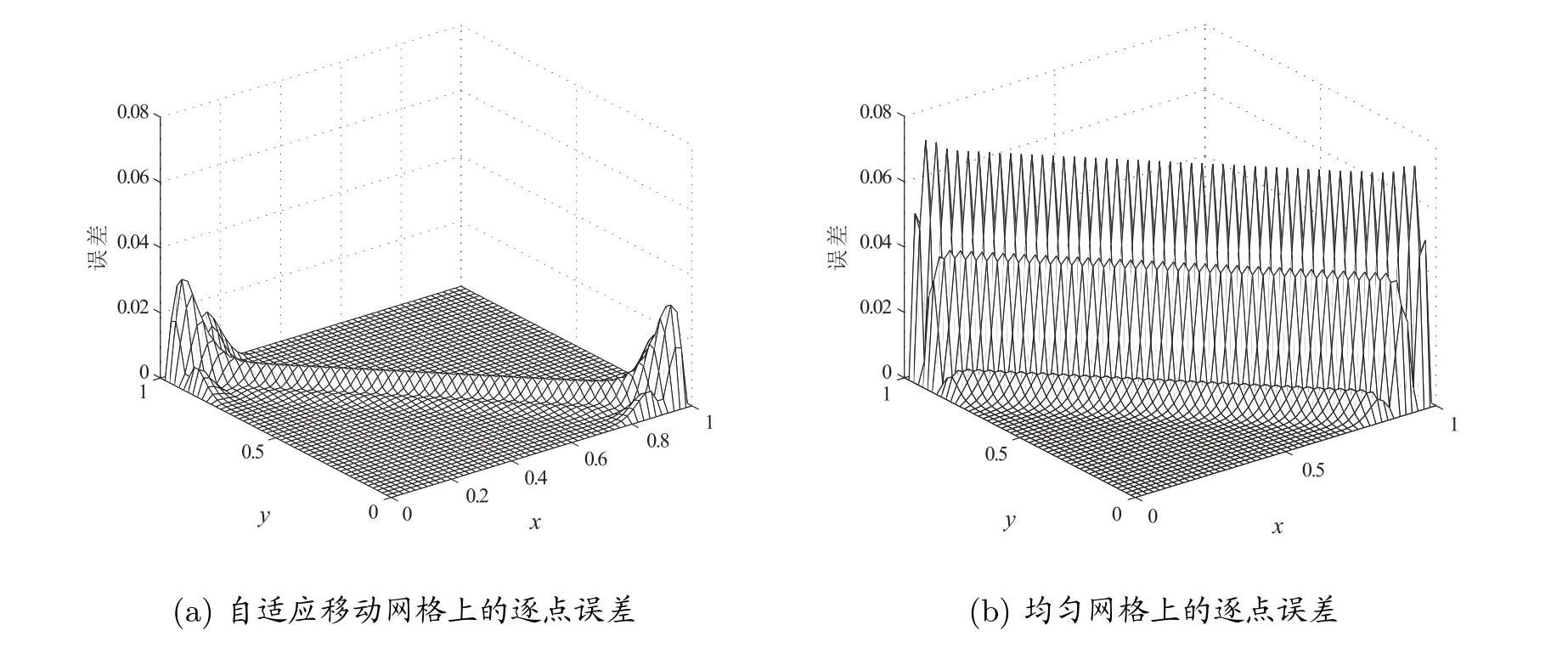
图3 t=0.5, ε=0.001 时，例1 中自适应移动网格与均匀网格上求解的逐点误差比较

表1 至表4 分别列出了两个算例中t= 0.1,0.2,0.3,0.4,0.5 时刻，网格剖分数分别取50×50、100×100、200×200 时，在自适应移动网格上获取的数值解与真解的L2误差和最大模误差。小参数ε的取值如表中所示。由表中数据可知该方法对于参数ε较小的情况是有效的，具有一定的收敛性。

表1 移动网格上求解例1 的L2 误差(ε=0.001)

表2 移动网格上求解例1 的最大模误差(ε=0.001)

表3 移动网格上求解例2 的L2 误差(ε2 =0.0001)

表4 移动网格上求解例2 的最大模误差(ε2 =0.0001)

综上，对于含源项二维抛物型奇异摄动问题(??)，使用自适应移动网格方法求解既能体现解在局部区域的特性，同时又能保证理想的求解精度。说明该方法对于二维抛物型奇异摄动问题的求解具有有效性和优越性。