多孔介质两相流耦合地应力问题的非线性混合有限元方法
刘子平, 李俊翔, 刘 琦, 马 强, 魏华祎
(1. 中国石油川庆钻探工程有限公司,成都 610051; 2. 四川大学数学学院,成都 610064;3. 湘潭大学数学与计算科学学院,湘潭 411105)
0 引言
在石油工程中,油藏模拟器是描述油藏中复杂流动机理的工具,大多数石油与天然气公司都使用油藏模拟器来设计与预测石油或者天然气的产出与效果。我国蕴藏着丰富的页岩气资源,其大规模开发将是我国满足天然气需求的重要途径和保障,但相对于传统油气资源,人们对于页岩气开采中流体流动机理认识还不是很成熟,而数值模拟是研究页岩气藏流动机理的重要手段,目前相关的数值模拟算法和软件与国外还有很大差距。
大多数模拟器都关注于孔隙介质中的流动过程,而结构本身的地应力则没有得到相对应的关注。事实上,多孔介质是可变形的,需要我们考虑流体流动与岩石变形之间的相互作用。在常规的固化岩石储层中,我们可以调整流动方程来充分描述地质结构中的低孔隙压缩性,刚度过载以及轻微的压降。但在非常规储层比如页岩气的开发中,非固化的介质、大的压降以及水力裂缝使得流动与结构变形之间的相互依赖与相互作用变得显著[?,?,?,?],从而必须对此现象进行显式地描述。这就需要我们建立流动与地应力相互耦合的数学模型并发展相应的数值计算方法来分析此类复杂问题。
在进行数值模拟中,大多数油藏系统都是非均匀的,它们由其流动性质上的空间变化来刻画,比如渗透率需要使用二阶张量进行描述。为此,在模拟中,我们有必要获得非常精确的速度分布,因为流体的流动路径将由速度方向决定。此外,得到关于饱和度解的准确描述也总是需要的。在石油工程数值模拟中,常常使用有限体积法或者单元中心有限差分离散来描述非变形的多孔介质,因为这些方法可以保证局部的质量守恒[?],而对于描述固体的变形,有限元方法则是更好的选择[6–7]。混合有限元方法通过将质量守恒方程与达西定律方程同时进行求解,既能满足局部的质量守恒也可以给出速度场更加精确与连续的描述[?,?,?]。由此,混合有限元方法也在描述多孔介质中的流动与岩体形变的耦合中得到了大量的使用[?,?,?,?,?,?,?,?,?,?]。
本文针对页岩气勘探开发过程中水气或水油两相流耦合的地应力计算与模拟问题展开研究,构建地质孔隙结构非线性两相流耦合地应力数学模型,提出合理的离散数值计算格式,构建相应的非线性混合有限元算法,并针对典型的两相流地应力问题进行计算模拟。
1 控制方程
为模拟带裂缝储层中的孔隙应力问题,孔隙介质中的流体流动与地应力产生了耦合,而地应力导致了岩石结构的线弹性变形。流体的流动与结构的应力应变充分耦合,需要在统一的系统下进行求解以保证精度与数值稳定性。一般地,我们首先推导两相流作用下的地应力耦合模型,基于两相流的质量守恒方程为



2 混合有限元分析与算法
下面对耦合地应力模型构建有限元算法,令未知量S0、vt、p、u分别属于函数空间
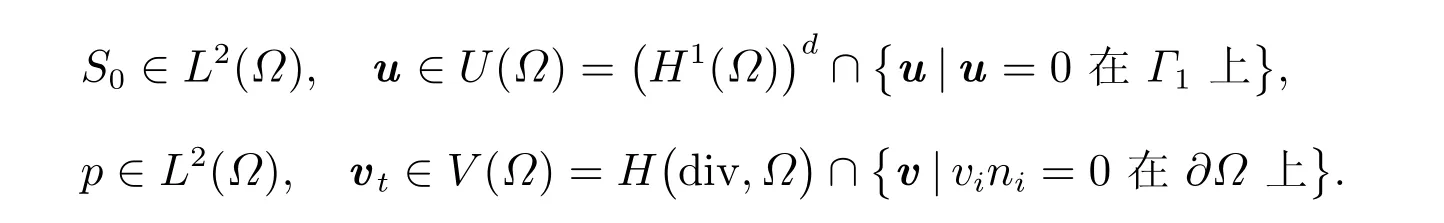
注意这里vini= 0 下标i为坐标分量求和,并非流体标识0 与1,表示在边界上法向速度的约束,即边界没有流体流出。由(??),可得到问题的弱形式为
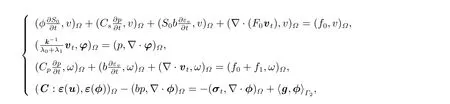
其中σt=bp0I+σ0+σeff,(·,·)Ω表示区域Ω上内积,〈·,·〉Γ2表示边界Γ2上内积,测试函数
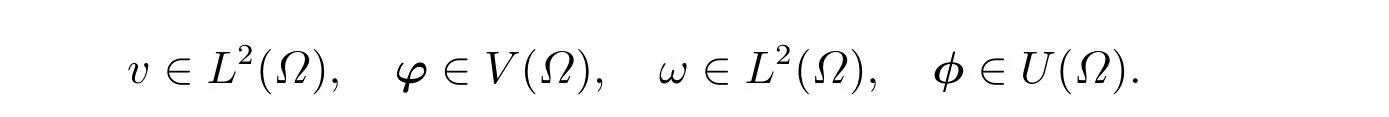

注意到左端整体矩阵中的子矩阵包含了未知量,并且右端项也包含了非知量。为简单起见,我们采用固定点迭代计算求解该非线性问题。由此建立有限元计算流程如下:

3 数值算例与讨论
3.1 无裂缝水驱油模型
下面给出数值算例,首先我们考虑一个均匀无裂缝区域下的水驱油两相流地应力模型。设模型中0 表示水相,1 表示油相,区域Ω=[0,10]2m2由32×32×2 的一致三角形单元离散,如图1 所示。

图1 正方形无裂缝岩石区域,使用三角形对区域作离散
表1 为岩石,水与油的材料参数,其中λ表示弹性拉梅第一常数,μ表示岩石剪切模量,由此可以得到四阶弹性系数张量为
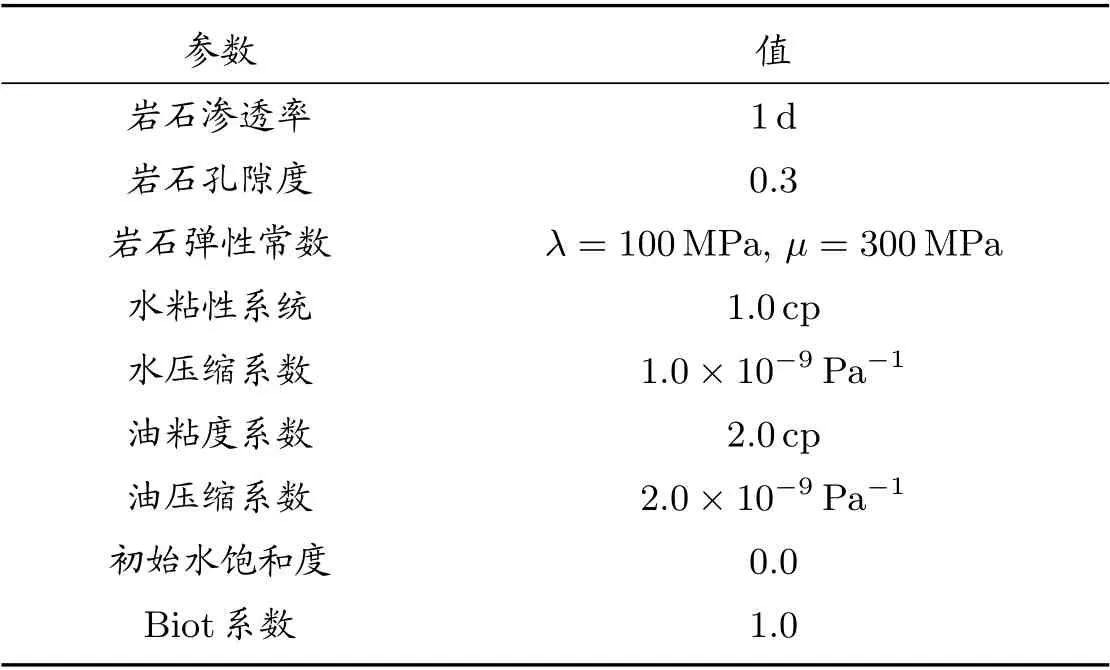
表1 岩石与液体参数
C=Cijkl=λδijδkl+μδikδjl+μδilδjk,

图2 给出了在模拟1 000 天注水后区域中的水饱和度、速度、压力、速度模量以及地应力模量的分布。图2(a)中饱和度的分布给出了注入水前端的均匀一致传播,我们可以看到与注入井相距相同的径向距离有相同的饱度值。这是因为储层具有均匀的性质,并且没有流体流出。图2(c)中的压力分布给出了一个在注入井处与产出井处的压力梯度,速度最高处位于注入井与产出井附近。计算得到的饱和度,压力,速度解显示了我们的算法能给出孔隙介质多相流动的准确物理行为。
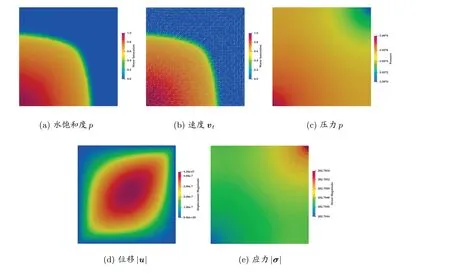
图2 均匀岩石结构注水1 000 天后的计算解
由于整个结构具有各向同性的弹性刚度,位移解与地应力非常光滑并且依赖于压力梯度,并且如我们所期望的,位移显示出关于对角线x=y的对称性。该模型的计算结果与文献[11]的结果相符,显示了我们构造的算法的正确性。
3.2 交叉裂缝水驱油模型
接下来,我们考虑如图3 所示的非均匀岩石储层区域。在区域中存在一个交叉裂缝,流体在该裂缝中具有更大的渗透率,设其为其它区域岩石渗透率的3 倍,模型的其它参数仍如表1 保持不变。由于裂缝尺寸较小,我们对区域进行如图3 所示的非结构化有限元网格剖分。与上节中的条件一样,我们仍然在左下角进行注水,油在右上角流出。模拟时间设置为152 天。

图3 交叉裂缝岩石区域以及非结构化有限元网格离散
图4 给出了在152 天时计算得到的水饱和度、速度、压力、位移以及地应力解。可以看到,裂缝区域中水的流动速度远大于在岩石中的流动速度,因此通过在左下角的持续注水,流体迅速沿对角线x=y上的裂缝流动。而在岩石中水的流动也受到影响并有向对角线靠拢的趋势。而在另外一条裂缝x+y=10 处,水的饱和度与无裂缝区域比较也明显增加。图4(b)所示的速度分布明显显示出裂缝区域的速度大于无裂缝区域的速度。由于裂缝分布的对称性,压力、位移与地应力也呈现出对称性,并且由于区域的非均匀性,计算得到的解明显没有均匀岩石区域的解光滑。
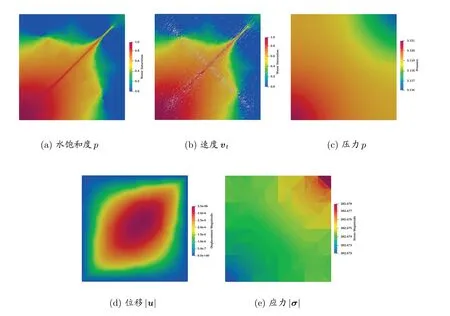
图4 非均匀交叉裂缝区域注水152 天后的计算解
4 结论与展望
本文建立了考虑裂缝储层的地应力两相流耦合模型,推导了地应力模型的非线性混合有限元离散格式,构建了二维非线性有限元计算流程,针对典型的带裂缝的水驱油模型问题,实现了非线性有限元计算模拟,验证了算法的正确性与有效性。
本文主要关注于有限元方法的工程应用,所考虑的模型相对较复杂,难以构造比较合适的真解实例,我们也没有对算法进行理论分析,主要通过检查计算结果是否符合物理实际做为评价结果正确性的标准。当然,在未来的工作中,我们不但要考虑更实际的三维问题,还要从理论层面对算法进行适当的分析,以期建立本文算法收敛性理论。
关于下一步的工作,一方面针对三维带裂缝的非均匀储层区域进行有效的建模,使用自适应有限元网格对区域进行更精细的离散,另一方面希望把适用于多边形和多面体的非标准有限元应用到该非线性问题的求解当中,并设计更高效稳健的算法和程序。
——北美又一种非常规储层类型

