一类矩阵方程约束最小二乘解的极秩
吴恒飞,张宗标
(亳州学院 电子与信息工程系,安徽 亳州 236800)
多年来,矩阵方程(组)解的极大秩、极小秩问题,一直是研究的热点问题,且取得了比较丰富的成果.其中文献[1]利用矩阵的奇异值分解和Frobenius 矩阵范数的性质,得到方程组AX=B,XC=D的极值秩和秩约束下的解表达式;文献[2]在X和Y为Reflexive (or anti-reflexive)矩阵和Hermitian reflexive(or anti-reflexive)矩阵的条件下,讨论了A-BXC和D-EYE*的矩阵表达式的极秩以及D-EYE*的极值惯性,并对结果进行了相关应用;文献[3]讨论了四元数矩阵方程AXA*+BYB*=C通解的复分量极秩公式;文献[4]讨论了在任意除法环上的线性矩阵方程A1X=C1,XB2=C2,A3XB3=C3,和A4XB4=C4的公共解的最大和最小秩的公式及其相关应用.
四元数矩阵方程AXA*=B在工程设计、信息论等科学技术领域应用广泛,文献[5]讨论了方程AXA*=B的Hermitian 解中子矩阵的极大秩和极小秩公式及相关应用,文献[6]讨论了方程AXA*=B在三对角加箭形矩阵约束下的Hermitian 解及最佳逼近解,文献[7]研究了四元数矩阵方程AXA*=B的非负定解存在的充要条件及通解表达式,给出了非负定解的极大极小秩公式及取得极秩的条件.
若四元数矩阵方程CX=D有解,则称方程CX=D是相容的,笔者主要讨论四元数矩阵方程:
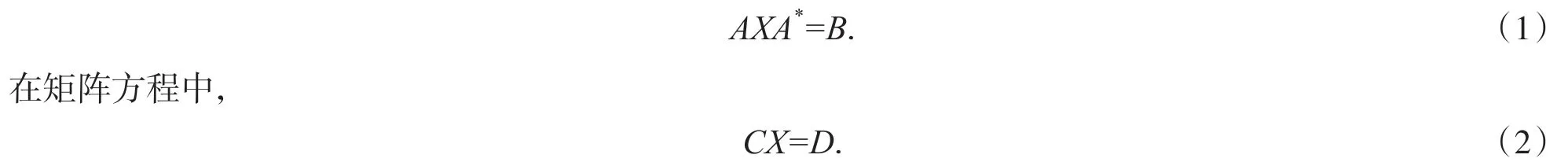
相容约束条件下的最小二乘解,并给出最小二乘解的极大秩、极小秩公式,其中A∈Hm×n,B∈Hm×m,C∈Hm×n,D∈Hm×n,是已知矩阵,X∈Hn×n是未知矩阵.

表1 符号说明
1 四元数矩阵方程AXA*=B 在方程CX=D 相容条件下的最小二乘解
引理1[8]四元数矩阵方程(2)相容的充要条件是CC+D=D,有解时,一般表达式为:

其中Y 是适当阶数的任意四元数矩阵.
引理2[9]A∈Hm×n,B∈Hn×m,C∈Hm×m为已知矩阵,X∈Hn×n是未知矩阵,矩阵方程AXB=C 的最小二乘解可以表示为:

其中U,V 是适当阶数的任意四元数矩阵.
引理3[10]设A∈Hm×n,B∈Ht×n,C∈Hm×s为任意矩阵,关于矩阵A 的广义逆A+和A 的左、右诱导算子分别为LA=I-A+A 和RA=I-AA+,具有如下性质:
(1)A+=(A*A)+A*=A*(AA*)+;
(2)LA=(LA)2=(LA)*,RA=(RA)2=(RA)*;
(3)LA(BLA)+=(BLA)+,(RAC)+RA=(RAC)+.
定理1若四元数矩阵方程(2)有解,在(2)有解约束条件下四元数矩阵方程(1)的最小二乘解可表示为:
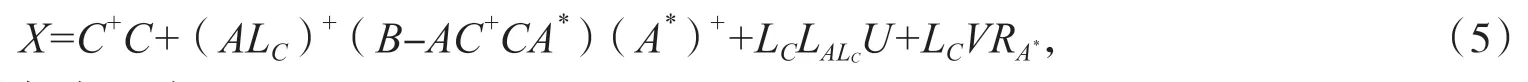
其中U,V 是适当阶数的任意矩阵.
证明由引理1 可知,若方程(2)是相容的,则其一般解为X=C+C+(I-C+C)Y,其中Y 是任意的矩阵,有:
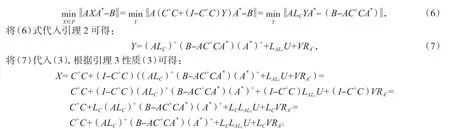
证毕.
定理1 给出四元数矩阵方程AXA*=B 在特殊约束条件下的最小二乘解的表达式,结果丰富了方程AXA*=B 的约束最小二乘解的理论.
2 最小二乘解的极大极小秩
引理4[11]已知A∈Hm×t,B∈Hm×k,C∈Hl×n是任意矩阵,则下列秩等式成立:
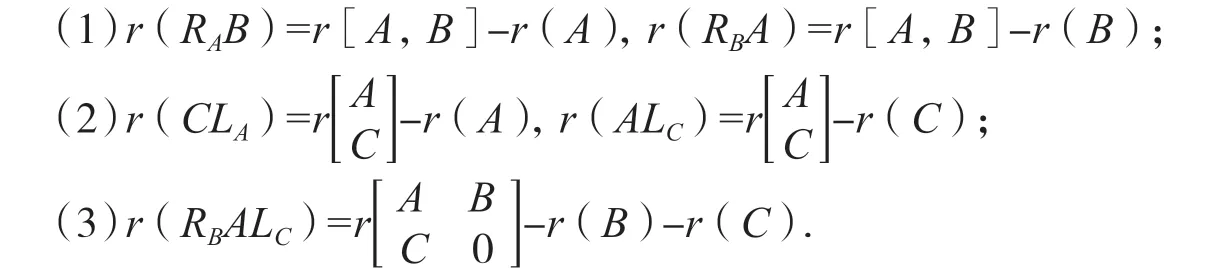
由引理4 可得引理5:
引理5已知矩阵A∈Hm×t,B∈Hm×k,C∈Hl×n,D∈Hs×k,C∈Hl×p是任意矩阵,则下列秩等式成立:
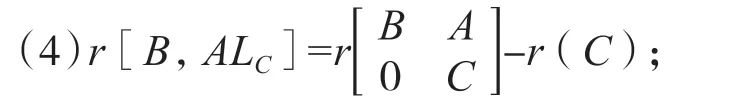

定理2 给出了四元数矩阵方程(1)在方程(2)相容约束条件下的最小二乘解的极秩公式,结果扩展了方程(1)的约束最小二乘解的极秩理论.
3 结语
本文讨论了四元数矩阵方程(1)在方程(2)相容条件下的最小二乘解及其极秩问题.方程(2)相容条件下,利用矩阵Moore-Penrose 广义逆,由定理1 获得了方程(2)最小二乘解表达式;利用分块矩阵Gaussian 变换和秩方法,由定理2 获得了方程(2)最小二乘解的极大、极小秩公式.文章结果扩展了约束四元数矩阵方程解的极秩理论,为约束四元数矩阵方程解的极秩问题提供参考.

