全平面上含混合核的Hilbert 型不等式及应用
2021-04-26 02:38有名辉范献胜何振华
韶关学院学报 2021年3期
有名辉,范献胜,何振华
(1.浙江机电职业技术学院 数学教研室,浙江 杭州 310053;2.广西财经学院 信息与统计学院,广西 南宁 530003)

其中c0=0.915 9…为Catalan 常数[2]. 2013 年,陈小雨等研究了式(4)的非齐次情形,并给出了参数推广[3].另外,刘琼研究了式(4)的推广[4]. 与式(3)和式(4)的相关联的其他文献可参照文献[5-8].值得指出的是,在Hilbert 型不等式诞生后的百余年间,通过不断创新核函数,研究者们还给出了大量新的Hilbert 型不等式[9-20]. 本文将建立含有新核的全平面上的Hilbert 型不等式,即:
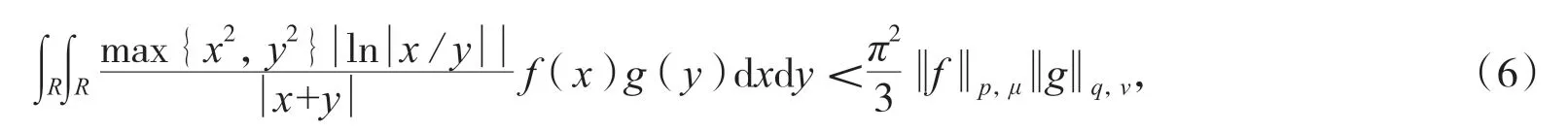
其中μ(x)=|x|2p-1,v(y)=|y|q-1.更一般地,笔者将构建多参数的积分核函数,建立式(5)、式(6)的推广形态,首先给出若干引理.
1 引理
引理1设γ>0,λ≥0,β1,β2>-λ,β1+β2=2n-λ+1. 且有:

将式(15)代入式(10),可得式(8).同理可得式(9).
引理2设γ>0,λ≥0,β1,β2>-λ,β1+β2=2n-λ+1. k(x,y)及C(β1,β2,λ,γ,n)由引理1 定义. ε 是充分小的正数,则当ε →0+时,有:


由此可知引理3 成立.
2 主要结果


3 推论


猜你喜欢
中学数学研究(广东)(2022年17期)2022-10-09
吉林大学学报(理学版)(2022年5期)2022-09-24
哈尔滨商业大学学报(自然科学版)(2022年4期)2022-08-18
新世纪智能(数学备考)(2021年5期)2021-07-28
非公有制企业党建(2020年9期)2020-09-26
中学生数理化·高三版(2019年1期)2019-07-03
领导决策信息(2017年12期)2017-05-17
中国卫生(2016年7期)2016-11-13
试题与研究·高考数学(2016年1期)2016-10-13
中国卫生(2014年10期)2014-11-12

