接触式轮廓仪自动标注模型分析

付美鑫

（长春汽车工业高等专科学校，吉林 长春130000）

全国大学生数学建模竞赛创办于1992 年，随着赛事的发展，参加竞赛的学校越来越多，尤其是专科组。本文将对2020年全国大学生数学建模竞赛D 题进行分析和求解。

2020 年全国大学生数学建模竞赛D 题是接触式轮廓仪的自动标注的问题，主要应用最小二乘法的思想，建立了接触式轮廓仪自动标注的模型，包括斜线模型、圆弧模型、旋转平移模型等，通过模型对工件需要标注的数据进行求解，并对工件进行标注。

1 问题简述

在工业生产中，工件表面测量方法分类很多，常见的分为接触式和非接触式[1]，其中接触式轮廓仪，广泛应用于光学元件、精密五金、机械加工等工件，在测量仪器中有着举足轻重的地位[2]。接触式轮廓仪在测量时，探针随着被测工件表面匀速滑行，上下移动，在X 和Z 方向分别采样，并通过传感器转化为电信号，经过计算机处理得到被测工件的表面轮廓图[3]。现要对表面轮廓图进行标注，主要标注的各项参数值包括：槽口宽度、圆弧半径、圆心之间的距离、圆弧长度、水平线段的长度、斜线段的长度、斜线与水平线的夹角和人形线的高度。有时在对工件做多次测量时，由于放置的水平位置和角度的不同导致测量结果有明显的差异，同时给轮廓图的标注带来很大的阻碍，建立相应的数学模型，完成以下问题：

1.1 标注工件1 的各项参数值。

1.2 针对有角度偏移和水平偏移的工件1 数据进行校正，对校正数据进行重新标注，并比较矫正后数据与原始数据标注之间的偏差。

图1 提取数据之后的轮廓图

1.3 针对工件2 给出的10 次测量数据，给出每次测量时的倾斜角度、并标注轮廓线的各项参数值，画出工件2 的完整轮廓图。

1.4 根据进一步给出的圆和角的测量数据，对1.3 中的结论进行修正，并完成轮廓线的修正。

2 问题分析

由于测量仪测量时在工件上匀速滑行，在X 和Z 方向进行采样，由于采样间距极短，且是等时间间隔获取，导致相邻很大部分数据差异不明显，本文所有模型建立求解所使用的数据都是每隔15 个数据进行提取一次，获取新数据。通过EXCEL 画图，可以清晰看到提取的数据保持工件原貌，（如图1 所示）。

3 模型建立与求解

针对问题一：以工件x=-1.77 为水平线，建立坐标系，要求解槽口宽度、斜线段长度、弧长、圆心之间的距离等，首先要建立斜线模型和圆弧所在圆的模型，然后利用交点，确定相应的槽口宽度、斜线段长度、人形线高度、弧长、圆心之间的距离等标注参数。其中，建立斜线模型：

zi= kxi+ b( k , b为 参数)；

图2 轮廓线标注图

在求解圆弧弧长与半径时，基于点到圆心距离等于半径理论，在工件凹槽处取最低点，以该点为中心，向前向后分别取20个数据，共计41 个点，利用点到圆心距离等于半径建立圆弧模型：

( xi- x0)2+ ( zi- z0)2= r2,( x0, z0, r 为参数)

对该线性方程组利用最小二乘法求解，即可得到圆弧的圆心及半径，从而确定圆弧的方程。

利用Mathematica 软件对上述斜线模型和圆弧模型进行求解，即可确定标注参数。对工件标注如图2。

针对问题二，根据旋转角度，与测量工件放置的位置及角度有变化，要对给出数据进行校正，首先要确定旋转角度，建立旋转平移校正模型，先旋转校正，然后进行平移校正，利用前面建立的数学模型进行求解，对工件进行参数标注。

旋转校正模型：

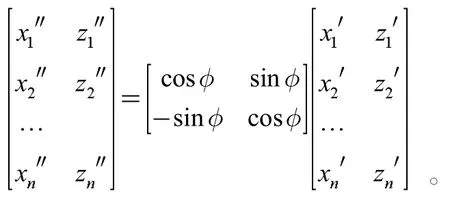
平移校正模型：

针对问题二，做误差分析如下：

对校对之后的工件轮廓图标注参数和工件1 的原始数据的工件轮廓图标注参数分类进行先对偏差分析（校对之后数据记为*），如下：

通过上述相对误差分析发现，水平距离的相对偏差较大，分析原因，主要是由于d9的实际距离较小，测量产生偏差属于合理范围之内，以后测量需要慎重。圆心间的距离偏差最小，在求解圆弧长度、圆心距离、半径时，主要是基于求解圆弧模型，其处理方式主要采取优化处理方法，产生的偏差非常理想，也说明了模型的合理性。

针对问题三：前两问基本解决工件自动标注问题，并建立相应的数学模型，要对工件2 进行标注，首先对所给工件2 测量的十组数据，利用问题二的数学模型进行旋转平移变换之后，对数据进行校正整合，拟合成一组数据，然后对获得的新数据，利用问题一的模型进行参数标注。在对工件2 进行标注时，10 次测量数据，每组数据都存在旋转和水平偏差，所以对10 组数据利用问题二的旋转校正模型和水平校正模型，对数据进行校正。首先确定每组数据旋转角度。通过问题二中旋转角计算模型，得到10 组数据旋转角如下表所示：

表1 工件2 的10 组数据旋转角

通过对工件2 的10 组数据进行分析，对旋转平移校正得到的数据，进行补充，主要补充缺失数据信息，得到工件2 的大致轮廓图，并对工件做简单标注。针对问题四：工件2 在问题三中已经基本标注完成，但是圆、角的标注还很粗糙，所以针对问题四，将对圆、角数据进行进一步的处理，然后对问题三的轮廓线进行修正。

4 结论

本文针对2020 年数学建模竞赛D 题进行分析求解，从模型求解结果和误差分析可以看出，该模型能够很好的对接触式轮廓仪测量的工件进行自动标注，并标注参数误差较小，该模型是有效的。由于时间问题以及技术硬件要求不足等问题，对于问题三和问题四，只做了数据的相关处理，在后续会进一步对其进行标注。

该模型不仅可以解决针对本文的问题，还可以应用于非球面接触式轮廓仪的自动标注、物体表面样貌的分析等其它测量的自动标注问题。